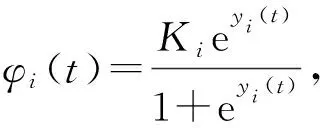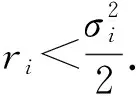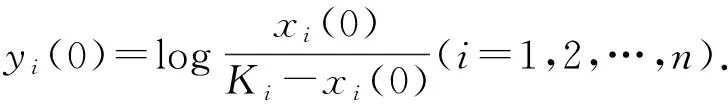随机多种群竞争系统的动力学行为
李海红,李海霞
(1.吉林建筑大学基础科学部,吉林 长春 130024; 2.长春光华学院商学院,吉林 长春 130024)
竞争行为广泛存在于各种生物种群中[1-5].Lotka-Volterra竞争系统可描述为
(1)
其中:xi是第i个种群的密度,ri是第i个种群的内禀增长率,Ki是第i个种群对环境的容纳量.若种群之间存在相互抑制的关系,则可以用竞争系统描述.这里考虑到环境白噪声的影响,随机微分方程为
(2)
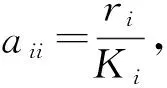
(3)
1 系统在均值意义下的持久性
在确定性系统中,文献[6]给出了均值意义下的持久性的定义.本文对随机系统也给出相应的定义.
定义1称系统(1)在时间均值意义下是持久的,是指
文献[4]研究了随机Logistic微分方程
得出如下结论:

由引理1和随机比较定理易得下面结论.
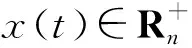
Φi(t)≤xi(t)≤φi(t),i=1,2,…,n,
且0<Φi(t) (5) 另外,Gray等[5]研究了带有随机扰动的SIS传染病模型 dI(t)=I(t)[(βN-μ-γ-βI(t))dt+σ(N-I(t))dB(t)]. (6) 其中:B(t)是一维的标准布朗运动;I(0)=I0∈(0,N),N是受传染病传染的人群数量.该文得到如下结论: 由上面结果显然可以得到: 即系统(3)在均值意义下是持久的. (7) 由Feller检验,尺度函数为 (8) 通过以上讨论,可得如下结论: [参 考 文 献] [1] 高芳.带有食饵避难的Leslie-Gower捕食者-食饵扩散系统的稳定性及最优税收[J].东北师大学报(自然科学版),2014(2):1-8. [2] GOH B S.Global stability in many species system[J].Amer Nat,1997,111:135-143. [3] FELLER W.An introduction to probability theory and its application:Ⅱ[M].New York:Willey and Sons,1971:1-137. [4] JIANG D Q,ZHANG B X.Existence uniqueness and global attractivity of positive solutions and MLE of the parameters to the logistic equation with random perturbation[J].Science in China,2007(7):977-986. [5] GRAY A,GREENHALGH D,HU L.A stochastic differential equation SIS epidemic model[J].SIAM J on Applied Mathematics,2011,71:876-902. [6] 陈兰荪,陈健.非线性动力系统[M].北京:中国科学技术出版社,1993:83-84.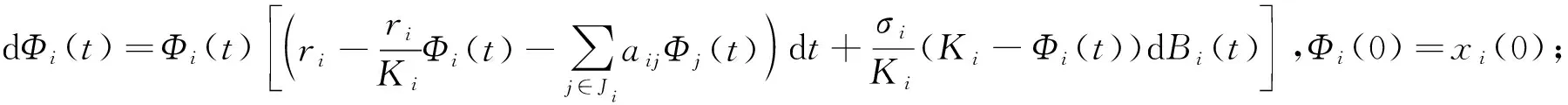
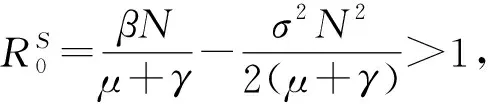


2 系统在均值意义下的非持久性