通货膨胀影响下时间一致的投资策略选择

刘文强，邱力军，杨 鹏

(西京学院理学院，陕西 西安 710123)

0 引言

投资策略选择问题是数理金融中一个热点问题.诺贝尔经济学奖得主Markowitz[1]第一次给出了投资策略选择问题，其给出的模型是离散的.最近30年来随着随机分析、带跳的随机微分方程以及倒向随机微分方程理论的发展，越来越多的学者研究连续模型中的投资策略选择问题.文献[2]引入线性二次控制法来研究最优投资问题，在其基础上，目前已有很多文献研究了连续时间投资策略的选择问题.[3-5]

近年来，随着经济社会的发展，通货膨胀变得越来越严重，人们资金贬值的速度在加快，所以研究基于通货膨胀影响的投资策略问题有很强的现实意义.在效用最大情形下，文献[6]考虑了最优投资-消费问题；文献[7]在部分信息下也研究了最优投资-消费问题；文献[8]研究了在均值-方差准则下，通货膨胀因素的投资策略.

上述提到的文献是时间不一致的，研究时间一致的投资策略更有意义.文献[9]考虑了经典保险风险的时间一致的均值-方差再保险-投资策略选择问题；Zeng等[10-11]研究了Heston模型在时间一致情形下的投资策略，并在风险资产带跳情形下，讨论了时间一致的最优策略选择问题；文献[12]也探讨了时间一致的投资策略选择问题，其考虑的风险资产满足CEV模型.另外，还有一些学者研究类似问题.[13-14]

基于上面的考虑，本文研究了通货膨胀影响下时间一致的投资策略.通货膨胀满足的随机微分方程和文献[6-8]一样，通货膨胀影响的处理方式类似于文献[8].通过使用随机控制理论，本文构造了一个检验定理，通过求解检验定理得到了时间一致的最优投资策略.最后，分析了一些模型参数对时间一致的最优投资策略的影响，解释了研究结果在经济学上的意义.

1 数理模型

设(Ω，F，F，P)为完备的附流概率空间.其中：P为概率；流F∶={F(t)|t∈[0，T]}关于F是右连续，关于P是完备的.金融市场包含一个无风险资产(债券)和一个风险资产(股票)，假设在金融市场上进行投资时，不考虑交易费用.无风险资产(债券)的价格为B(t)，满足方程dB(t)=r(t)B(t)dt，其中r(t)>0表示利率.风险资产(股票)的价格P(t)满足方程

dP(t)=P(t)[μ(t)dt+σ(t)dW1(t)].

这里μ(t)≥r(t)表示风险资产的平均收益率，σ(t)>0表示风险资产的波动率，{W1(t)，t≥0}是标准布朗运动.

类似文献[6-8]，本文也假设物价水平L(t)满足随机微分方程

dL(t)=L(t)[a(t)dt+b(t)dW2(t)].

(1)

其中：a(t)是期望通货膨胀率；b(t)为通货膨胀扩散率；{W2(t)，t≥0}是一维标准布朗运动，表示影响物价指数水平的随机因素.现实中，影响风险资产(股票)价格与影响物价水平的随机因素可能相关，假设相关系数为ρ(t)，即〈W1(t)，W2(t)〉=ρ(t).

设投资者在时刻t具有财富x(t)，投资在风险资产上的金额为π(t)，余下的资金投资到无风险资产(债券)上，所以投资之后盈余过程x(t)满足如下的随机微分方程：

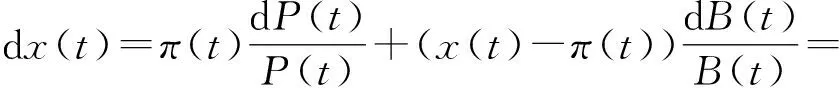
(2)

由于本文考虑了通货膨胀影响，假设考虑通货膨胀后的真实财富为y(t)，y(t)=x(t)/L(t).对y(t)应用It公式得到y(t)满足随机微分方程

dy(t)=y(t){[m(t)+n(t)π(t)]dt+σ(t)π(t)dW1(t)-b(t)dW2(t)}，

(3)

这里m(t)=r(t)-a(t)+b2(t)，n(t)=μ(t)-r(t)-b(t)σ(t)ρ(t).

定义1投资策略π(t)称为可行的，若满足：

(ⅰ)π(t)关于F循序可测，且为右连左极的；

(ⅲ) 随机微分方程(3)关于策略π(t)有唯一的强解.

记所有可行的保险和投资策略的集合为Π.

2 时间一致的最优投资策略

与文献[10]类似，定义目标函数为

(4)

其中：(t，y)∈T×R；Et，y[·]=E[·|y(t)=y]；γ>0为常数，表示投资者的风险厌恶系数.

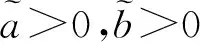
则称π*(t，y)为平衡策略，对应的平衡值函数是V(t，y)=V(t，y，π*).

和文献[10]一样，利用定义2得到时间一致策略刚好等于平衡策略；通常的最优值函数恰好等于平衡值函数.下文称平衡策略u*与平衡值函数为最优时间一致策略和最优值函数.

3 问题求解

这里对于财富盈余过程(3)求解时间一致的最优投资策略与最优的值函数.和文献[13]中的定理2.1或文献[14]中的定理2.1类似地给出如下的检验定理.

定理1(检验定理) 设F(t，y)，G(t，y)，H(t，y)定义在[0，T]×R上，它们关于t连续、可微，关于y二阶连续、可微，即F，G，H∈C1，2.如果F，G，H满足方程：

(5)

(6)

(7)

则：

V(t，y)=F(t，y)，G(t，y)=Et，y[y(T)]，H(t，y)=Et，y[y2(T)]；

(8)

π*(t)是时间一致的最优投资策略，满足

证明本定理的证明可参考文献[13]中的定理2.1或者文献[11]中的定理2.1，本文不再证明.

从(4)式和定理1可得

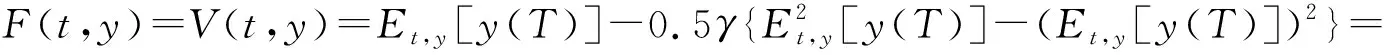
所以

H(t，y)=G2(t，y)+0.5γ[G(t，y)-F(t，y)].

(9)

综合考虑盈余过程的结构和边界条件F(T，y)=y和G(T，y)=y，与文献[9]与[14]类似地构造F(t，y) 和G(t，y)为：

F(t，y)=A(t)y+B(t)/γ，A(T)=1，B(T)=0；

(10)

G(t，y)=C(t)y+D(t)/γ，C(T)=1，D(T)=0.

(11)

其偏导数如下：

Ft=A′(t)y+B′(t)/γ，Fy=A(t)，Fyy=0；

Gt=C′(t)y+D′(t)/γ，Gy=C(t)，Gyy=0.

把F(t，y)和G(t，y)的表达式，(9)式，以及上面的各偏导数代入(5)式得

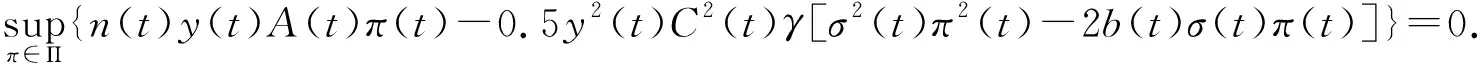
(12)

设f(π(t))=n(t)y(t)A(t)π(t)-0.5y2(t)C2(t)γ[σ2(t)π2(t)-2b(t)σ(t)π(t)]，f(π(t))关于π(t)求导数得

(13)

将(13)式代入(12)式整理得

(14)

从而

(15)

(16)

将(13)式代入(6)式中整理得

(17)

故

(18)

(19)

综合(15)—(18)式，

(20)

(21)

(22)

通过上述讨论有如下定理.

定理2对于财富过程(3)，最优的时间一致的投资策略为

(23)

平衡值函数为

(24)

在最优策略和终止时刻T下，财富过程的方差为

(25)

证明结合(13)和(20)式，可以得到(23)式；由(10)，(20)和(21)式，可得(23)式；由(19)—(11)与(20)—(22)式，可以得到(25)式.

4 数值算例及经济意义分析

这里给出模型参数改变时参数对最优投资策略的影响，同时分析所得到的投资策略对现实中保险人进行再保险和投资的指导意义.

例1取μ(t)=0.04，r(t)=0.02，σ(t)=0.05，γ=0.2，ρ(t)=0.2，y(t)=10，T-t=2，b(t)=0.4，a(t)∈[0.01，0.04].图1给出了a(t)对时间一致的最优投资策略π*(t)的影响.从图1可以看出π*(t)关于a(t)单调递增，a(t)是期望通货膨胀率，说明随着通胀率的增大，投资人希望加大在风险资产上的投资资金，以此减小资金贬值的速度.

例2取μ(t)=0.04，r(t)=0.02，σ(t)=0.05，γ=0.2，ρ(t)=0.2，y(t)=10，T-t=2，a(t)=0.04，b(t)∈[0.1，0.4].图2给出了b(t)对时间一致的最优投资策略π*(t)的影响.从图2可以看出π*(t)关于b(t)单调递减，b(t)为通货膨胀扩散率，也就是说随着通货膨胀不确定因素的增加，投资者会减小在风险资产上的投资额.

图1 a(t)对π*(t)的影响

例3取a(t)=0.04，r(t)=0.02，σ(t)=0.05，γ=0.2，ρ(t)=0.2，y(t)=10，T-t=2，b(t)=0.4，μ(t)∈[0.03，0.06].图3给出了μ(t)对时间一致的最优投资策略π*(t)的影响.从图3可得π*(t)是μ(t) 的单调递增函数，μ(t)是风险资产的平均收益率，表明μ(t)增大投资者从风险资产上的投资收益将增大，投资者会冒风险进行投资.

例4取μ(t)=0.04，b(t)=0.4，σ(t)=0.05，γ=0.2，ρ(t)=0.2，y(t)=10，T-t=2，a(t)=0.04，r(t)∈[0.01，0.03].图4给出了r(t)对时间一致的最优投资策略π*(t)的影响.从图4可得π*(t)是r(t) 的单调递减函数，r(t)是无风险资产的利率，说明随着r(t)的增大投资者从无风险资产上投资的收益将增加，因此会减少在风险资产上的投资金额.

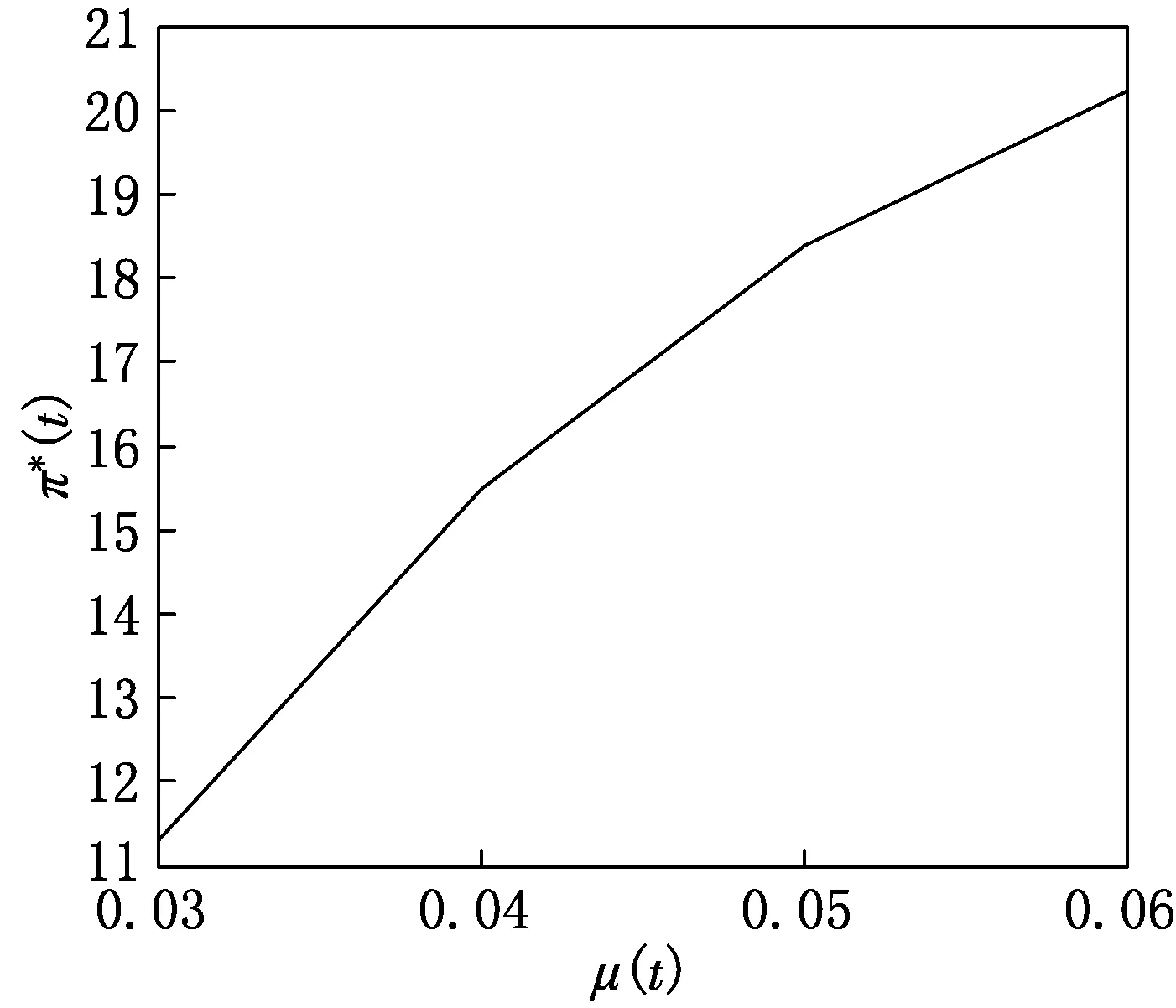
图3 μ(t)对π*(t)的影响

例5取μ(t)=0.04，r(t)=0.02，a(t)=0.04，γ=0.2，ρ(t)=0.2，y(t)=10，T-t=2，b(t)=0.4，σ(t)∈[0.05，0.08].图5给出了σ(t)对时间一致的最优投资策略π*(t)的影响.从图5可知π*(t)是σ(t) 的单调递减函数，σ(t)是风险资产的波动率，σ(t)增大表明投资风险增大，因此投资者会减少在风险资产上的投资金额.

例6取μ(t)=0.04，r(t)=0.02，σ(t)=0.05，γ=0.2，b(t)=0.4，y(t)=10，T-t=2，a(t)=0.04，ρ(t)∈[-0.2，0.2].图6给出了ρ(t)对时间一致的最优投资策略π*(t)的影响.从图5可知π*(t)是ρ(t) 的单调递减函数，ρ(t)表示风险资产和通货膨胀因素之间的相关系数，说明随着相关性增大，投资者会减少在风险资产上的投资金额.

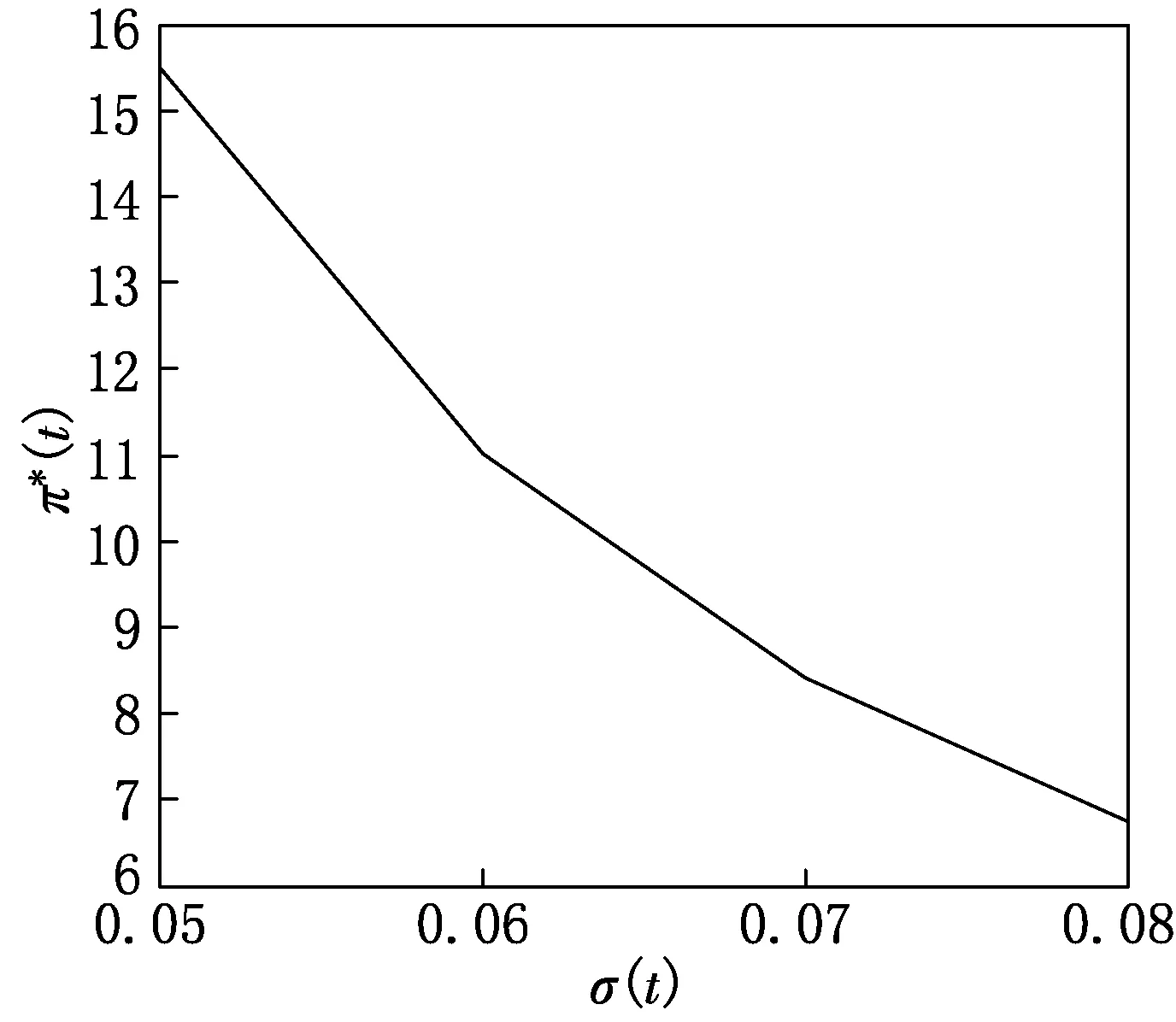
图5 σ(t)对π*(t)的影响

[参 考 文 献]

[1] MARKOWITZ H M.Portfolio section[J].Journal of Finance，1952，7(1)：77-91.

[2] ZHOU X，YIN G.Markowitz’s mean-variance portfolio selection with regime switching：a continuous-time model[J].SIAM Journal on Control and Optimal，2003，42(4)：1466- 1482.

[3] XIE S X.Continuous-time portfolio selection with liability and regime switching[J].Insurance：Mathematical and Economics，2009，45(1)：148-155.

[4] 杨鹏.均值-方差准则下CEV模型的最优投资和再保险[J].系统科学与数学，2014，34(9)：1100-1107.

[5] LIANG Z，BI J，YUEN K，et al.Optimal mean-variance reinsurance and investment in a jump diffusion financial market with common shock dependence[J/OL].Mathematical Methods of Operations Research，2016[2016-09-26].doi：10.1007/s00186-016-0538-0.

[6] BRENNAN M J，XIA Y.Dynamic asset allocation under inflation[J].Journal of Finance，2002，57(3)：1201-1238.

[7] BENSOUSSAN A，KEPPO J，SETHI S P.Optimal consumption and portfolio decisions with partially observed real prices[J].Mathematical Finance，2009，19(2)：215-236.

[8] 姚海祥，姜灵敏，马庆华，等.考虑通货膨胀因素下的连续时间均值-方差投资组合选择[J].控制与决策，2013，28(1)：43-48.

[9] LI Z F，ZENG Y，LAI Y Z.Optimal time-consistent investment and reinsurance strategies for insurers under Heston’s SV model[J].Insurance：Mathematics and Economics，2012，51(1)：191-203.

[10] ZENG Y，LI Z F.Optimal time-consistent investment and reinsurance policies for mean-variance insurers[J].Insurance：Mathematics and Economics，2011，49(1)：145-154

[11] ZENG Y，LI Z F，LAI Y Z.Time-consistent investment and reinsurance strategies for mean variance insurers with jumps[J].Insurance：Mathematics and Economics，2013，52(3)：489-507.

[12] LI D P，RONG X M，ZAO H.Time-consistent reinsurance-investment strategy for an insurer and a reinsurer with mean-variance criterion under the CEV model[J].Journal of Computational and Applied Mathematics，2015，283：142-162.

[13] BJORK T，MURGOCI A，ZHOU X Y.Mean variance portfolio optimization with state dependent risk aversion[J].Mathematical Finance，2014，42(1)：1-24.

[14] KRONBORG M T，STEFFENSEN M.Inconsistent investment and consumption problems[J].Applied Mathematics and Optimization，2015，71(3)：473-515.