单圆柱微波谐振法测量热力学温度的研究
崔 劲, 冯晓娟, 林 鸿, 张金涛, 宦可为
(1. 长春理工大学 理学院, 长春130022; 2. 中国计量科学研究院 热工计量科学研究所, 北京 100029)
1 引 言
热力学温度单位——开尔文(K)是国际单位制7个基本单位之一,其准确测量是修订国际温标的基础。2019年,国际单位制将发生重大变革,即采用基本物理常数重新定义包括温度单位开尔文在内的4个基本单位,温度单位开尔文将定义在玻尔兹曼常数上[1],之后,国际温度计量界将实施新的开尔文,其中热力学温度的测量是重要方向之一[2]。
基准热力学温度测量方法主要包括定容气体温度计、气体声学基准温度计、气体介电常数基准温度计、气体折射率基准温度计、噪声温度计、多普勒展宽温度计以及辐射温度计[3~5]等。近些年,随着国际上玻尔兹曼常数测定研究的不断深入,气体声学、介电常数和噪声温度计得到了迅速发展[6~11],成为当前测量热力学温度不确定度较小的3种方法。本课题组主要开展了圆柱气体声学温度计和圆柱气体折射率温度计的研究[12~14],两种方法均可将热力学温度的测量转换为谐振频率的测量,具有良好的发展前景。
气体折射率热力学温度计通常采用氦气作为工质,主要原因是氦气量子力学“从头算”(ab initio method)获得的物性参数可达到较高的精度[15]。然而,由于使用氦气测量时,需要使得谐振腔工作在较高的压力下,谐振腔的变形较大,材料等温压缩系数引入的测量不确定度成为限制该方法测量热力学温度的主要来源[12]。本文对采用氩气作为工质的单圆柱气体折射率温度计进行了探索研究,相比氦气,工作压力可下降10倍。开展了253 ~303 K热力学温度测量研究,分析了氩气物性数据对热力学温度测量不确定度的影响,讨论了该方法的未来发展趋势。
2 气体折射率温度计测量原理
通过实际气体的维里状态方程可知,在气体压力小于10 MPa的条件下,压力p、热力学温度T以及气体密度ρ满足式(1)的关系:
p=RTρ[1+Bρ(T)ρ+Cρ(T)ρ2+…]
(1)
式中:R为通用气体常数;Bρ(T)和Cρ(T)分别为第二和第三密度维里系数,可通过量子力学“从头算”计算得到。已知压力p与密度ρ,可由气体维里系数方程得到热力学温度T。
式(1)压力可准确测定,密度ρ可从气体折射率n计算得到。气体折射率与气体的相对介电常数εr和相对磁导率μr有关,即n2(p,T)=εrμr。根据Clausius-Mossotti方程和Lorentz-Lorenz方程,非极性气体的相对介电常数率和相对磁导率可以分别按密度展开成维里方程的形式:
(2)
(3)
根据式(2)和式(3)可以得到气体折射率的维里方程:
(4)
式中:Aε,bε和cε分别为第一,第二和第三介电维里系数;Aμ和bμ是第一和第二磁导维里系数。Schmidt和Moldvover[16]采用精密环形电容器以氦气“从头算”结果为参考,测量了273~303 K氩气的相对介电常数,并给出了第一介电维里系数Aε=4.142 03(15)cm3/mol,在水三相点得到第二介电常数bε(T)是 0.28 cm3/mol和0.31 cm3/mol之间,是目前不确定度最小的测量结果之一;氩气的第一磁导率维里系数测量结果是Barter等[17]总结了不同研究组,并指出当温度压力不太高和不太低时,氩气第一磁导率维里系数可以近似为Aμ=-0.000 080 9(6)cm3/mol。
氩气的折射率由光学方法或微波谐振的方法可精确地得到,但光学器件不太适合温度变化较大的环境;近年来采用微波谐振法测量气体折射率得到了较大的发展。在前期的玻尔兹曼常数测量研究[18]中积累了充分经验的基础上,本文采用微波谐振法测定气体折射率。
根据电磁场理论,在理想条件下,圆柱形谐振腔的TM(横磁)模式对应的谐振频率为:
(5)
式中:R和L表示圆柱腔的半径和长度;l、m、n分别为轴向、角向和径向的半波数;χmn为第一类m阶贝塞尔函数的第n个根;c为电磁波在谐振腔内的传播速度,c=c0/n,其中c0为光在真空中的传播速度。通过测量单圆柱微波谐振腔真空状态和氩气压力p时的谐振频率,可得到氩气的折射率:
(6)
式中:f和Δf为谐振腔内微波谐振频率测量值和非理想因素的修正;下标0和p代表真空和被测压力的状态,非理想因素包括趋肤效应、腔体壁面材料的电导率、微波天线的开孔和导管尺寸等;κT为谐振腔材料的等温压缩系数,等温压缩系数可由超声共振频谱法测量得到[19]。根据测量的折射率,通过式(4)可求解密度ρ,结合测量的压力p,可得到热力学温度T。
3 实验系统
本文建立的基于微波谐振法通过氩气折射率测定热力学温度的实验装置如图1所示。实验系统包括无氧铜圆柱谐振腔、压力舱、微波谐振频率测量系统、温度测量与控制系统以及压力测量与控制系统等。
实验本体的圆柱谐振腔,采用纯度为99.97%锻压无氧铜棒加工而成,其电导率高、磁性低、相同条件下微波谐振频率的能量品质因数较高;腔内圆柱面和端盖内表面均采用目前最为先进的超精密宝石刀切削工艺加工而成,满足实验测量的精度要求。压力舱为谐振腔提供了一个相对稳定的压力和温度环境,减小了由于恒温槽温度波动对谐振腔内气体温度带来的影响。压力舱置于槽内液体恒温槽里进行实验。为了进一步提升谐振腔的温度稳定性,谐振腔外侧缠薄膜型电阻加热带,采用PID控制。图2和图3是实验测量中谐振腔内的温度和压力的变化,在24 h内谐振腔的温度稳定性为±0.2 mK,压力稳定性为±5 Pa。
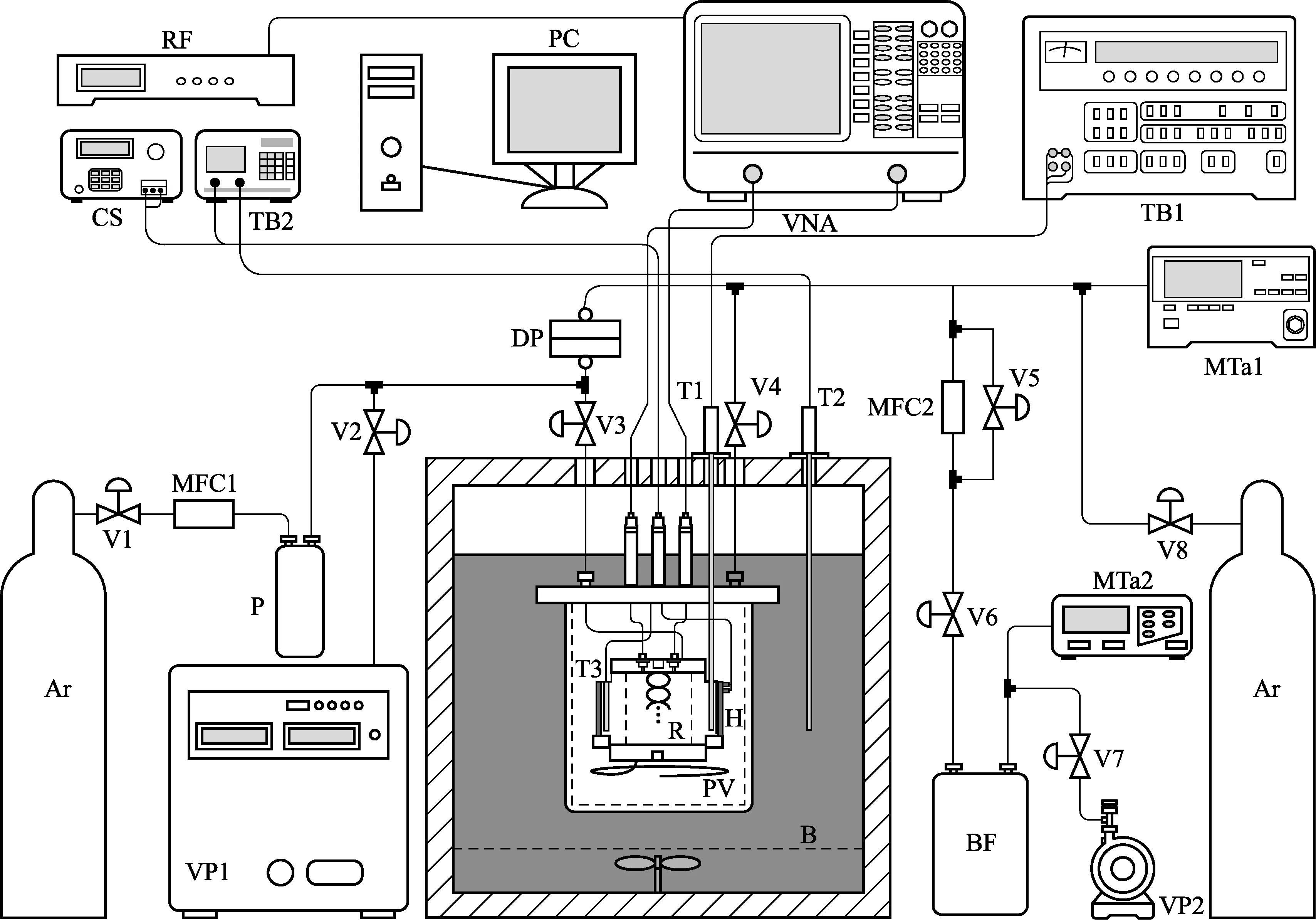
图1 气体折射率温度计实验系统示意图Fig.1 Sketch of the gas refractive index primary thermometry experiment systemB—恒温浴;PV—压力舱;R—谐振腔;T1~T3—标准铂电阻温度计;H—加热片;PC—计算机;VNA—矢量网络分析仪;TB1、TB2—测温电桥;RF—铷钟频率参考源;CS—程控电流源;MTa1、MTa2—数字绝对压力计;MFC1、MFC2—气体质量流量计;P—气体纯化器;DP—金属隔膜压差计;BF—气体缓冲罐;VP1、VP2—真空泵;V1~V8—阀门
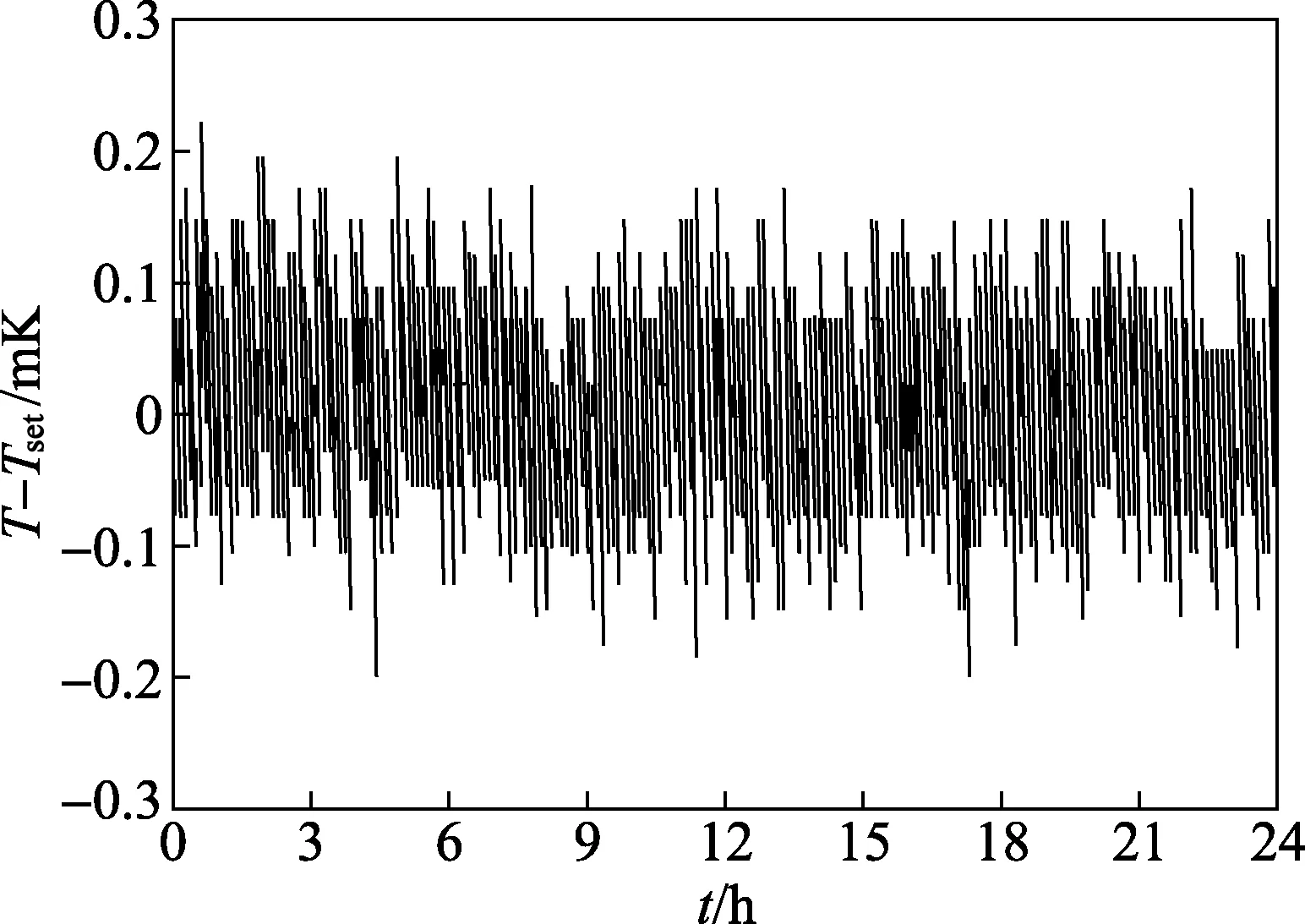
图2 谐振腔温度稳定性Fig. 2 Temperature stability of the cavity
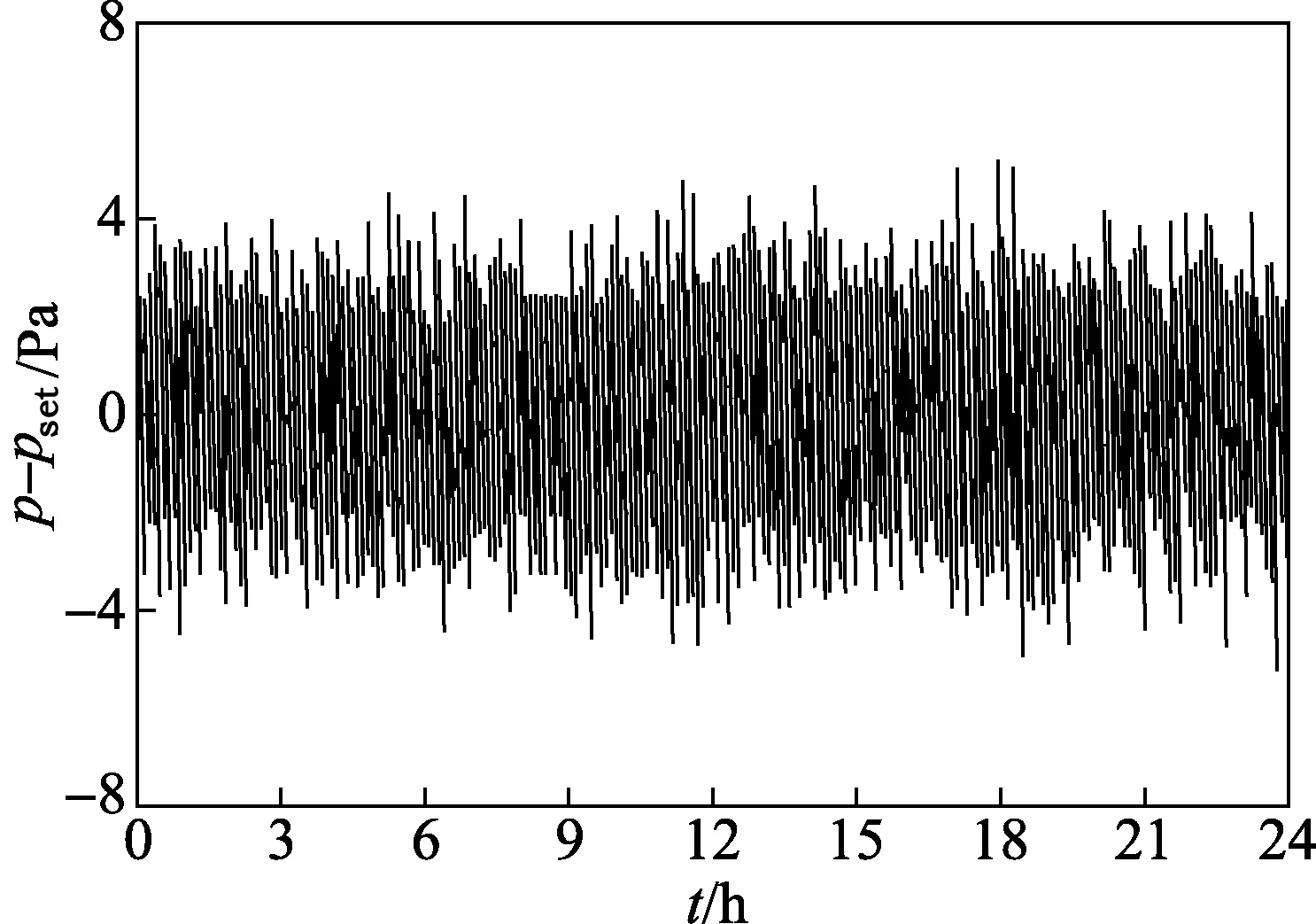
图3 谐振腔内气体压力稳定性Fig.3 Pressure stability of the gas in the cavity
本实验采用的高纯氩气为美国Air Products 气体公司提供的BIP plus高纯氩气,其标称气体纯度为99.999 97%。根据生产商提供的报告,气体杂质主要是H2O、O2、CO2、CO、总碳氢化合物(THC)以及挥发性有机化合物(VOCs)等,实验中将高纯氩气进一步通过纯化器,去除可能的可反应气体;同时通过质量流量控制计控制谐振腔内气体的匀速缓慢流动,保证气体纯度和压力的稳定。
数据采集系统以美国国家仪器公司(NI)的LabVIEW软件为开发平台,编写和集成了微波谐振频率测量、温度测量与控制、压力测量与控制、气路控制以及降压、进气过程自动控制等实验测量与控制软件程序,实现了实验系统测量的自动化和数据的自动采集。
4 实验测量结果与讨论
4.1 热力学温度的计算方法
实验中,分别测量不同温度下压力为700 kPa和真空环境下不同TM模式的谐振频率fp和f0,修正非理想因素扰动效应后代入式(6),计算中得到700 kPa压力下氩气的折射率n;然后通过式(4)折射率与密度的关系得到密度ρ;再由式(7)计算热力学温度T:
(7)
采用与水三相点温度TTPW测量结果进行比较的相对法可极大降低实验测量中与温度无关的非理想因素带来的影响。实验中采用4个TM模式微波谐振频率获得气体折射率,不同微波模式得到的氩气折射率一致性优于1×10-8,在同一温度下可计算得到各模式对应的热力学温度。表1给出的热力学温度结果为4个测量结果的算术平均值。
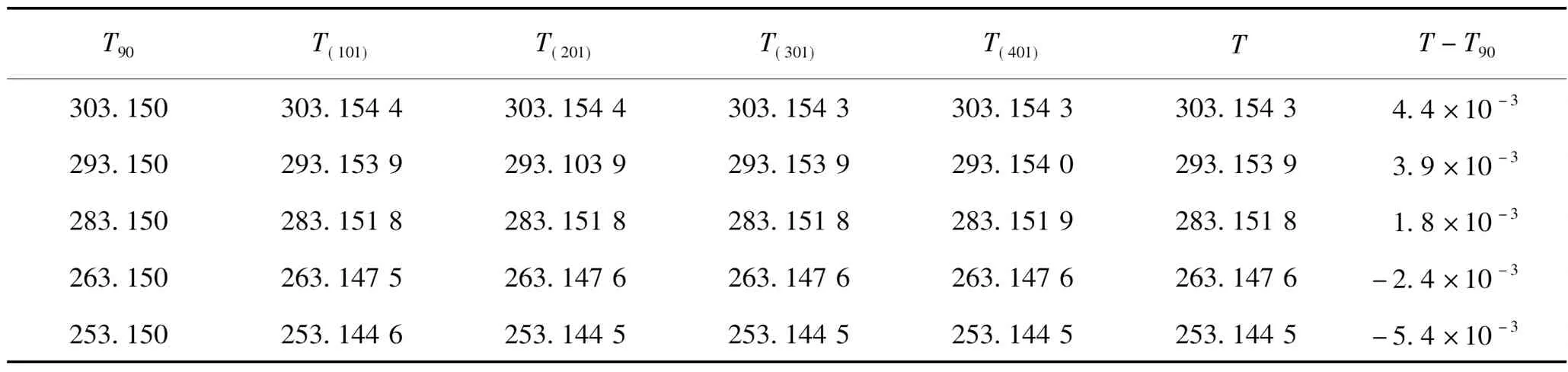
表1 热力学温度测量结果Table 1 The result of thermodynamic temperature measurements K
4.2 实验测量结果
实验测量了汞三相点(234.315 6 K)到镓融化点(302.914 6 K)温区内5条等温线的热力学温度T及其与ITS-90温度T90的差异(T-T90)。表1中T(101)、T(201)、T(301)和T(401)表示4种TM模式计算得到的热力学温度。根据国际温度咨询委员会(CCT)的建议,将结果表示为T-T90,如图4所示。图4中,黑点为本文测量结果,虚线为CCT第四工作组根据当前最精密的T-T90测量结果给出的评估曲线,双点划线为评估曲线的不确定度。
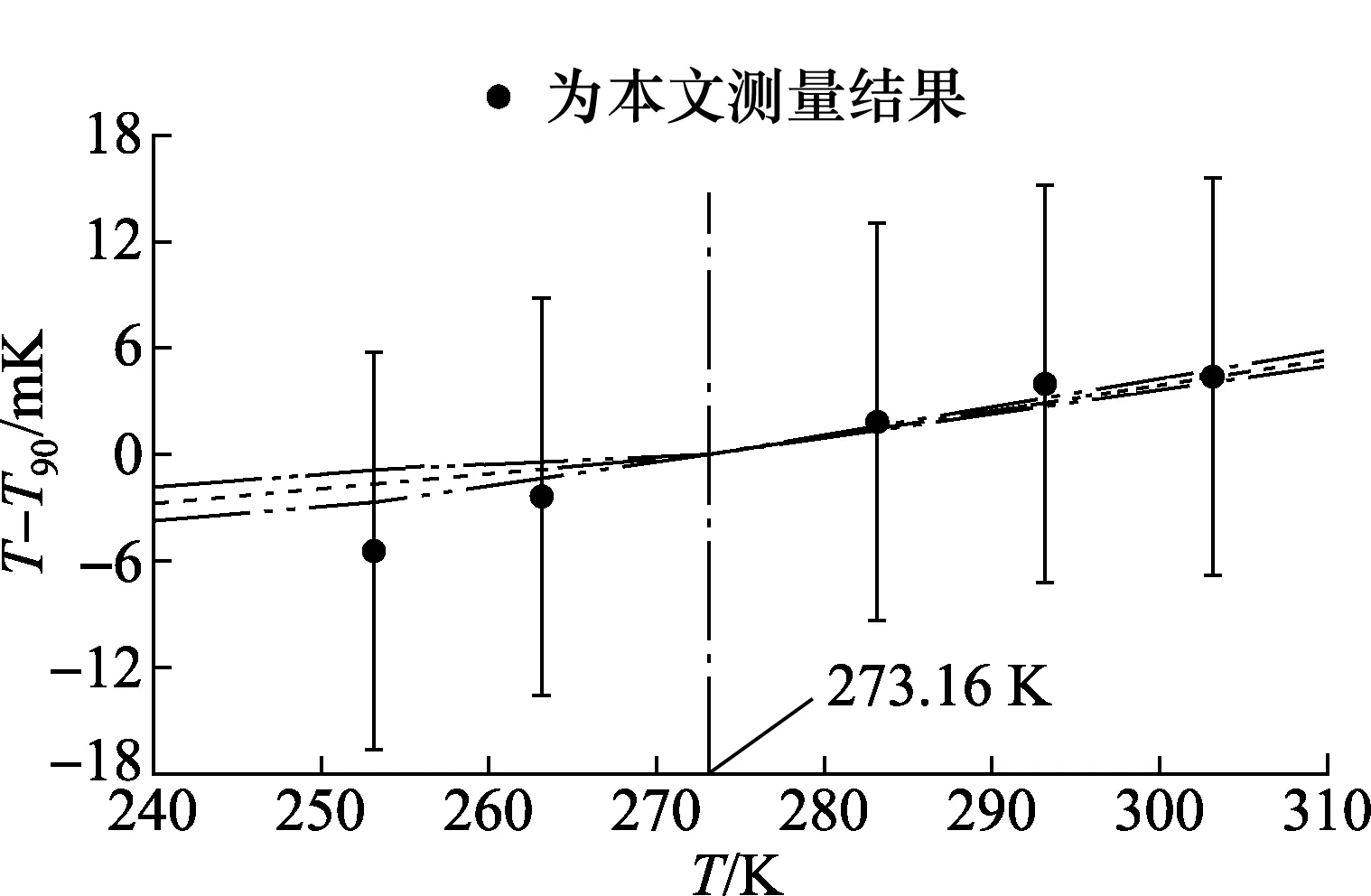
图4 热力学温度与 ITS-90温度的偏差(T-T90)分布Fig.4 The difference between the thermodynamic temperature and the ITS-90 temperature (T-T90)
4.3 实验测量不确定度分析
本文测量的(T-T90)的不确定度主要包括热力学温度T的不确定度和ITS-90温度T90的不确定度。其中T90的不确定度u(T90)来源列于表2,主要包括温度计检定引入的不确定度、电阻测量引入的不确定度、ITS-90非一致性和温场稳定性引入的不确定度。
采用微波谐振法测量热力学温度的不确定度u(T)主要来源于4个部分,包括压力测量引入的不确定度、微波谐振频率引入的不确定度、氩气各项物性参数引入的不确定度以及等温压缩系数引入的不确定度。
每次实验开始之前和之后,压力测量设备均在中国计量科学研究院压力实验室进行校准。实验中采用MT210 表压计、MT210绝压计以及MKS差压力测量获得工作氩气的压力。MT210表压力计测量范围为0~700 kPa,由表3可以看到在长时间的测量环境下,表压力计具有良好的稳定性。
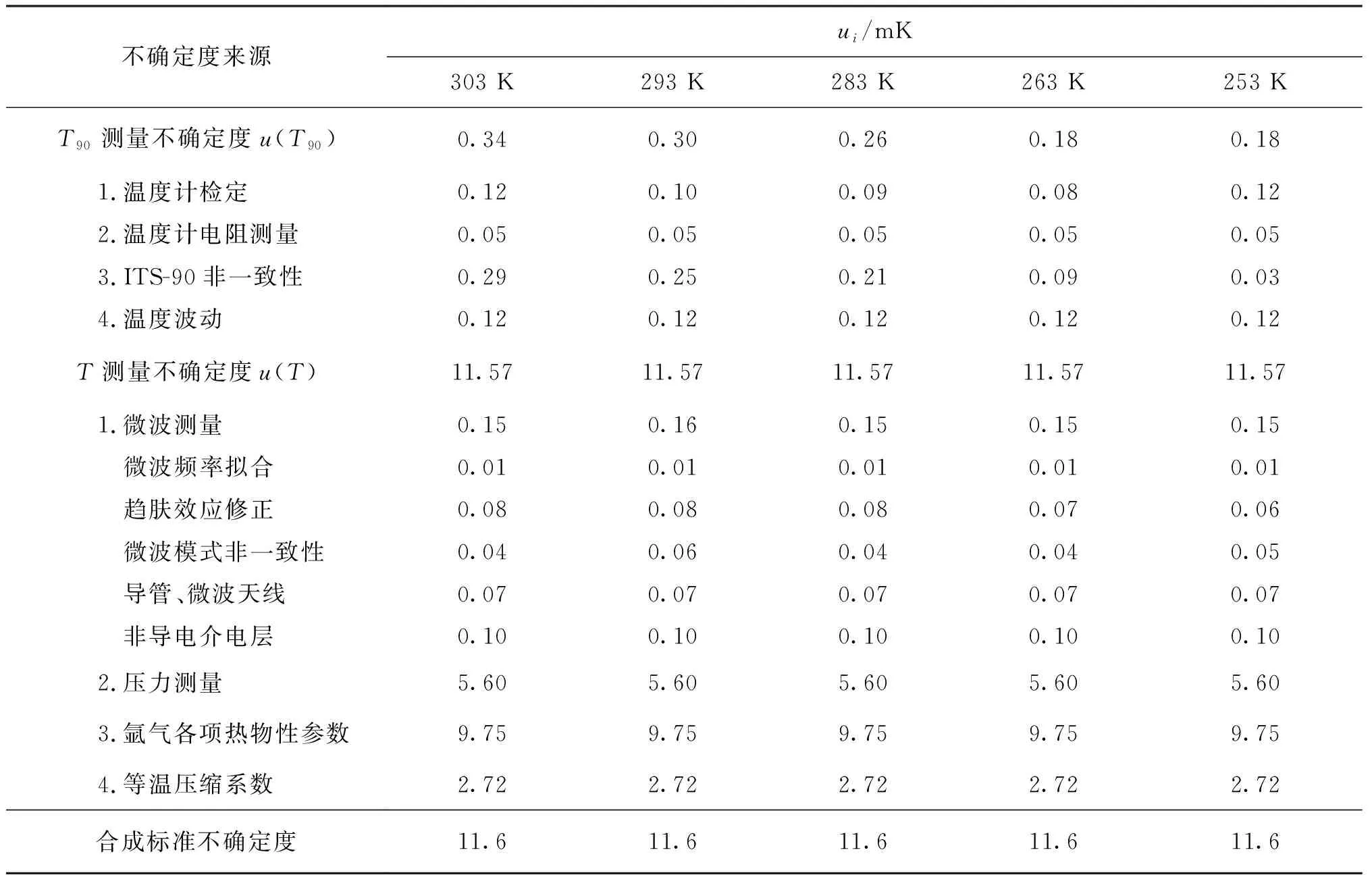
表2 T-T90的测量不确定度Table 2 The uncertainty budget of T-T90
微波谐振频率测量中部分与温度无关的非理想因素的影响,如气体导管、微波天线以及腔体壁面电导率等,通过不同温度的比值可以抵消,对于热力学温度测量的影响可以忽略。对于热力学温度测量而言,微波测量的不确定度主要包括微波频率拟合、趋肤效应的影响以及微波模式的非一致性。
在根据折射率计算密度的过程中,相对介电常数,介电维里系数和磁导维里系数均具有不确定度,计算了各物性不确定度对热力学温度的影响,见表4。其中第一介电和磁导维里系数不随温度变化,第二和第三维里系数均为温度的函数,表4所列为273.16 K参数值;同时,还计算了实验测量的不同温度下第二和第三维里系数不确定度对热力学温度的影响,均为表4所列结果。
本文使用的等温压缩系数通过超声共振法测量得到[19],其共振峰的匹配误差RMS为0.694%,对热力学温度测量产生的不确定度也列于表2。
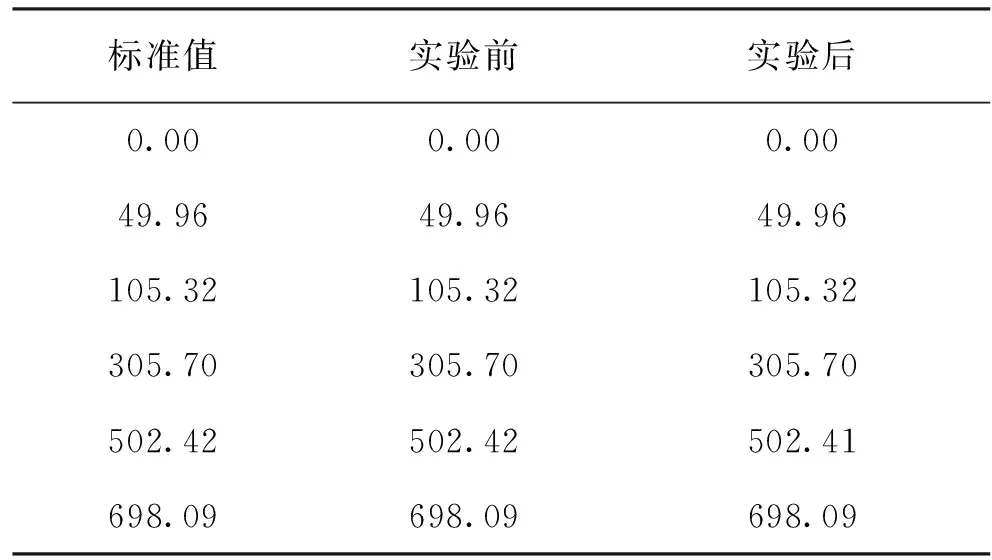
表3 压力计MT210校准结果 kPa

表4 氩气各项热物性参数对热力学温度的影响Table 4 The uncertainty contribution from thermalphysical properties of argon
由表2可以看出,采用单圆柱微波谐振法,利用氩气为工质的气体折射率温度计,热力学温度测量的不确定度主要来源于压力测量引入的不确定度和氩气热物性参数引入的不确定度。可以预期,未来通过改进压力测量不确定度,如采用活塞式压力计进行测量或者使用双圆柱法消除压力测量的影响,测量结果的不确定度会进一步降低。
受限于当前氩气量子力学“从头算”和相关实验测量结果的不确定度,采用氩气为工质的气体折射率温度计测量不确定度要大于以氦气为工质的气体折射率温度计,而随着量子力学理论计算的快速发展,采用氩气气体为工质的气体折射率温度计仍具有良好的前景。对于某些领域,如对热力学温度测量不确定度要求不太高的场合,使用工作压力较低、对杂质不敏感的氩气气体折射率温度计更为合适。
5 结 论
本文建立了单圆柱气体折射率温度计测量系统,以氩气为工质开展了253 ~303 K的热力学温度测量研究,分析了影响测量结果不确定度,并与国际温度咨询委员会的评估值进行了比较,具有良好的一致性。
对于氩气气体折射率温度计,氩气热物性参数对热力学温度测量带来的影响最大,为9.75 mK,对热力学温度测量不确定度要求不太高的场合,使用工作压力较低、对杂质不敏感的氩气气体折射率温度计具有良好的前景。未来,随着氩气物性参数理论计算和实验系统压力测量不确定度的深入研究,采用氩气气体为工质的气体折射率温度计的测量不确定度也将进一步得到改善。
[参考文献]
[1] Fischer J, Ullrich J. The new system of units [J].NaturePhysics, 2016, 12(1):4-7.
[2] White D R, Fischer J. The Boltzmann constant and the new kelvin [J].Metrologia, 2015, 52(5): S213-S216.
[3] Fischer J. Progress towards a new definition of the kelvin [J].Metrologia, 2015, 52 (5) :S364-S375.
[4] 段宇宁, 林鸿, 张金涛,等. 基准声学温度计的研究进展[J]. 计量学报, 2007, 28(3A): 1-6.
Duan Y N, Lin H, Zhang J T,etal. Review on the Primary acoustic gas thermometry [J].ActaMetrologicaSinica, 2007,28(3A):1-6.
[5] 付云丰, 屈继峰, 张建强,等. 噪声温度计中新型数字相关器设计 [J]. 计量学报, 2014, 35(4):335-338.
Fu Y F, Qu J F, Zhang J Q,etal. A new design of digital correlator for Johnson noise thermometry [J].ActaMetrologicaSinica, 2014, 35(4):335-338.
[6] de Podesta M, Underwood R, Sutton G,etal. A low-uncertainty measurement of the Boltzmann constant [J].Metrologia, 2013, 50(4): 354-376.
[7] Pitre L, Sparasci F, Risegari L,etal. New measurement of the Boltzmann constant k by acoustic thermometry of helium-4 gas [J].Metrologia, 2017, 54(6): 856-873.
[8] Gavioso R M, Madonna Ripa D, Steur P P M,etal. A determination of the molar gas constant R by acoustic thermometry in helium [J].Metrologia, 2015, 52(5):S274-S304.
[9] Feng X J, Zhang J T, Lin H,etal. Determination of the Boltzmann constant with cylindrical acoustic gas thermometry: new and previous results combined [J].Metrologia, 2017, 54(5):748-762.
[10] Gaiser C, Fellmuth B, Haft N,etal.. Final determination of the Boltzmann constant by dielectric-constant gas thermometry [J].Metrologia, 2017, 54(3): 280-289.
[11] Qu J F, Benz S P, Coakley K,etal. An improved electronic determination of the Boltzmann constant by Johnson noise thermometry [J].Metrologia, 2017, 54(4): 549-558.
[12] 谷学敏, 林鸿, 冯晓娟, 等. 定程圆柱声学基准温度计初步研究 [J]. 仪器仪表学报, 2013, 34(3): 502-508.
Gu X M, Lin H, Feng X J,etal. Preliminary study on the fixed-path-length cylinder primary acoustic thermometer [J].ChineseJournalofScientificInstrument, 2013, 34(3): 502-508.
[13] 林鸿, 蔡杰, 冯晓娟, 等. 双圆柱微波谐振测量热力学温度的研究 [J]. 工程热物理学报, 2013, 34(6):1018-1021.
Lin H, Cai J, Feng X J,etal. Thermodynamic thermometry measurement based on microwave resonance at two Cylinders [J].Journalofengineeringthermalphysics, 2013, 34(6):1 018-1 021.
[14] 蔡杰,林鸿,冯晓娟,等. 圆柱共鸣腔力学特性模拟分析[J]. 计量学报, 2015, 36(2):141-144.
Cai J, Lin H, Feng X J,etal. Simulation and Analysis of the Mechanical Properties of Cylindrical Resonator[J].ActaMetrologicaSinica, 2015, 36(2):141-144.
[15] Rourke P M C, Hill K D. Progress toward development of low-temperature microwave refractive index gas thermometry at NRC [J].InternationalJournalofThermophysics, 2014, 36(2-3):205-228.
[16] Schmidt J W,Moldover M R. Dielectric permittivity of eight gases measured with cross capacitors [J].InternationalJournalofThermophysics, 2003, 24(2):375-403.
[17] Barter C, Meisenheimer R G, Stevenson D P. Diamagnetic susceptibilities of simple hydrocarbons and volatile hydrides [J].JournalofPhysicalChemistry, 2002, 64(9):1 312-1 316.
[18] Zhang K, Feng X J, Zhang J T,etal. Microwave measurements of the length and thermal expansion of a cylindrical resonator for primary acoustic gas thermometry [J].MeasurementScienceandTechnology, 2017, 28(1):015006.
[19] 鲍静, 冯晓娟, 林鸿, 等. 可变温的固体材料弹性参数测量系统研究[J]. 计量学报, 2015, 36(5):449-454.
Bao J, Feng X J, Zhang J T,etal. Study on the Setup for Measurement of Temperature-dependent Elastic Properties of Solids [J].ActaMetrologicaSinica, 2015, 36(5):449-454.
[20] Huot J, Bose T K. Experimental determination of the dielectric virial coefficients of atomic gases as a function of temperature [J].TheJournalofChemicalPhysics, 1991, 95(4): 2683-2687.
[21] Moldover M R, Gavioso R M, Mehl J B,etal. Acoustic gas thermometry [J].Metrologia, 2014, 51(1):R1-R19.

