一种用于测量重力梯度的扭秤装置
余 烨, 胡 翔, 熊 超, 石文静, 涂良成
(1. 湖北省计量测试技术研究院, 湖北 武汉 430071;2. 华中科技大学 物理学院 重力导航教育部重点实验室, 湖北 武汉 430074;3. 华中科技大学 武汉国家光电实验室, 湖北 武汉 430074)
1 引 言
重力位的二阶导数可以很好地描述地球重力场的特征,且其空间分辨率比重力更高,适用于探测研究局部小地质体及其细节。重力梯度仪是一种测定重力场梯度信号的仪器[1,2],由于传统的扭秤重力梯度仪解释重力梯度数据的方法比较落后、测量的工作效率很低、设备笨重等缺点而逐渐被其它重力梯度仪器所取代,但是其具有结构简单、造价低廉、测量精度高等优点,因此采用扭秤测量重力梯度的方法并没有消失[3~6]。
本文设计了一款新型的扭秤重力梯度仪,考虑到传统的重力梯度数据提取方法的落后性,采用整体最小二乘法,该方法同时考虑到系数矩阵与观测向量的误差,可精确地提取梯度数据,并给出相应的精度估计;考虑到扭秤悬挂系统稳定的时间过长,极大地影响了重力梯度的测量效率,采用PID控制技术,设计了一款振幅衰减系统,该系统能够快速实现振幅衰减,可极大地提高扭秤的工作效率。
2 扭秤测量重力梯度的原理
厄缶扭秤系统一般由金属秤杆、2个检验质量、铂铱合金轻质细丝组成。金属秤杆非常细而且较长,其一端的检验质量用较长的轻质细丝悬挂,另一端检验质量直接与金属杆相连,如图1所示。图1中Oxyz为实验室坐标系,Oξηz为与扭秤悬点固连的坐标系, 沿着秤杆长方向,ξ沿着秤杆短方向,η沿着铅垂线方向。2个检验质量由于位置的差异,所感应水平加速度不同,而扭丝通过扭转一定的角度,记录水平方向的待测力。扭丝感应的力矩包含2个部分:一部分与曲率梯度有关,另一部分与水平梯度有关。选择适当的坐标系,就可以建立待测力矩与重力梯度的联系。

图1 厄缶扭称结构示意图
扭秤系统的引力矩为:
mlhWyzcosα-mlhWxzsinα
(1)
式中:α为方位角;J为转动惯量;m为检验小球的质量;l为半杆长度;h为轻质悬丝的长度;Wxz与Wyz分别为水平方向的重力加速度沿着z轴的变化,即水平重力梯度;WΔ与Wxy为曲率重力梯度,与重力等位面的不均匀性有关。
扭秤在受到外界的引力矩作用时,运动方程可以写为:

(2)
式中:θ为扭丝偏转的角度;β为阻尼系数;k为悬丝扭转系数。方程的解可以写成如下形式:
(3)
式(3)包括2部分:第1部分表示扭秤自由振动过程;第2部分表示扭秤振动过程中,所在的平衡位置。其中ω0为扭秤的本征频率,A0、φ0分别为扭秤的初始振幅与相位。
在静态测量时,仅仅需要提取扭秤运动的平衡位置,而忽略它的自由振动过程,那么扭丝的偏转角度与外部恒定力矩可以写成如下的关系:
M(α)=kΔθ=k(θ-θ0)
(4)
式中θ0为悬丝不受任何外力作用时的偏转角度。扭秤的力学平衡方程可以简化为:
mlhcosαWyz-mlhsinαWxz
(5)
由于地球重力场不均匀,因此式(5)中的θ0当做未知量来处理,式(5)有5个未知数。所以要想得到重力梯度值,需要在同一点设置不同的方向(α不同)上测量5次。
3 实验装置
扭秤重力梯度仪的核心在于扭秤的设计。厄缶扭秤是传统扭秤中测量梯度信号最多的装置,因此主要借鉴它的原理,设计一种新的扭秤重力梯度仪,该装置结构如图2所示。

图2 扭秤重力梯度仪结构示意图
对应的力学平衡方程为:
f1Wxycos 2α+f2Wyzcosα
(6)
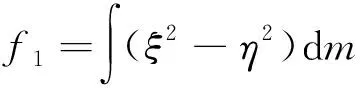
扭秤重力梯度仪主要由转台、真空系统、扭秤系统、角度测量系统、振幅衰减系统5部分组成。转台用来改变扭秤的方位角。真空系统用来维持扭秤的工作环境。扭秤系统用来测量曲率、水平重力梯度,是梯度仪的核心部分,主要由悬丝、秤杆、两根竖杆等组成,石英玻璃具有密度低且均匀性好、杂质含量少、热膨胀系数低、杨氏模量高的特点,被选做为秤杆材料,同时为了避免静电干扰,玻璃秤杆的表面镀上一层金属薄膜,其设计尺寸为200 mm×12 mm×14 mm;秤杆的两端的上表面与下表面通过粘贴的方式分别配置一个尺寸为15 mm×12 mm×100 mm钛合金重荷,该方式与细丝悬挂检验质量的方法相比,大大的减小了悬挂系统的稳定时间,同时也避免了检验质量摆动对重力梯度测量的影响;当然也存在一定的缺点,相同的检验质量,厄缶扭秤通过轻质细丝悬挂,两个检验质量的相对竖直距离可以放得更远,而本结构无法避免虚空,相对距离较近,降低了扭秤的灵敏度;悬丝是goodfellow公司生产纯度为99.9%、直径为50 μm、长度为500 mm的钨丝,其一端与旋转导引相连,另一端通过套管与夹具粘贴在秤杆上表面的中心,通过旋转导引可以改变扭秤系统的平衡位置,同时也可以在初始状态调节扭秤的振幅,快速使扭秤进入测量状态。角度测量系统由自准直仪、石英窗口、反射镜、秤杆组成,用来监测扭秤的运动状态。其中将秤杆的前表面作为反射镜,采用ELCOMAT 3000 自准直仪作为角度测量装置。扭秤没有受到外力的作用下,反射镜与自准直仪标准线的夹角为θ0,当扭秤受到不均匀的重力作用时,平面镜与自准直仪的夹角为θ,反射镜转过的角度就为钨丝的偏转角。振幅衰减系统如图3所示,通过在秤杆两侧加上两对反馈极板,与秤杆构成电容,采用静电反馈的模式来控制扭秤在平衡位置,实现扭秤振幅的快速衰减,从而使扭秤系统进入测量状态,之后关闭振幅衰减系统,实现待测力矩的静态测量;但是,该系统仅衰减振幅作用,达到目的后,停止工作,不会对重力梯度造成影响。

图3 振幅衰减系统
整个伺服系统的闭环控制框图如图4所示。其中Rin为输入的参考偏转角度;Re为残差信号;u为PID控制器的输出电压;τ为执行机的控制力矩;Rout为扭秤的偏转角度;Rf为自准直仪的输出;HP(s)为PID控制器的传递函数;HA(s)为执行器的传递函数;HT(s)为为曲率重力梯度被控对象的传递函数;HO(s)为自准直仪的传递函数。

图4 闭环控制系统框图
4 实验数据仿真
4.1 扭秤系统稳定时间的模拟
为了评估扭秤悬挂系统的稳定时间,本文选用simulink软件仿真。采用MATLAB的非线性的工具箱,通过设定相关的控制指标,系统会自动地找出最佳的PID参数,仿真结果如图5所示。
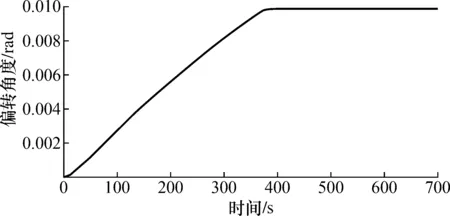
图5 阶跃信号模拟图
取PID参数P=10 000,I=0,D=10 000,振幅衰减 10 000 μrad时,控制所需的时间约为7 min,可极大提高扭秤的测量效率(传统扭秤,悬挂系统的稳定时间为20~30 min,效率提高了3~4倍),同时考虑到扭秤的运动周期(9~10 min)以及每个测点的极限测量次数(6次),扭秤重力梯度仪的重力梯度测量的极限效率约为1 h。
4.2 重力梯度数据精度提取模拟
式(6)有5个未知数据,传统上在每一个测点进行5个方位的测量,然后联立5个方程,最后求出梯度值。该方法很难对重力梯度的不确定度进行合理的评估,而整体最小二乘法提供了合适的处理方案[7~8]。
影响重力梯度的一级误差项来源于有结构系数f1、f2以及扭秤的方位角αi、钨丝的扭转系数k、角度测量系统θi的测量不确定度。设计的误差分配如表1所示。

表1 误差分配表
采用整体最小二乘法对21个测点的重力梯度值[9]进行大量的随机误差数值仿真(其中每一个测点进行10 000组数据模拟,每一组模拟包含12个力学平行方程,及对应扭秤系统的12个方位),曲率、水平重力梯度信号的最大精度估计如图6所示。

图6 重力梯度误差分布模拟
从图6中可以得到,重力梯度的最大精度估计全部都在0.1~0.3E(1E=1×10-9m/s2)之间,且WΔ、Wyz和Wxz的精度大约是Wxy精度的两倍,设计精度优于0.5E。
5 结束语
设计了一款扭秤重力梯度仪,可以测量曲率、水平重力梯度,经仿真测量精度优于0.5E,设计的扭秤振幅衰减系统可快速实现扭秤振幅的衰减,使扭秤快速进入测量状态,测量一组重力梯度数据的极限效率约为1h,与传统的扭秤重力梯度仪相比极大地提高了测量效率。
[参考文献]
[1] 蔡体菁, 周百令. 重力梯度仪的现状和前景[J]. 中国惯性技术学报, 1999, 7(1): 39-42.
[2] Szabo Z. The history of the 125 year old Eotvos torsion Balance[J].ActaGeodGeophys, 2016, 51:273-293 .
[3] Bod L, Fischbach E, Marx G,etal. One Hundred years of the Eotvos Experiment[J].ActaPhysicaHungarica, 1991, 69: 335-355.
[4] Hansen R. The gravity gradiometer basic concepts and tradeoffs[J].TheLeadingEdge, 1999, 18(4):478-480.
[5] Edwin H, Leeuwen V. BHP develops airborne gravity gradiometer for mineral exploration [J].TheLeadingEdge, 2000, 19(12):1296-1297.
[6] Pawlowski B. Gravity gradiometer in resource exploration[J].TheLeadingEdge, 2012,17 (1):51-52.
[7] Huffel S, Vandewalle J. The Total Least Squares Problem: Computational Aspects and Analysis[M]. Philadel Phi:Society of Industrial and Applied Mathematics,1991.
[8] Golub G H, Hoffman A, Stewart G W. A generalization of the Eckart-Young-Mirsky matrix approximation theorem [J].LinearAlgebra&ItsApplications, 1987, 88-89(3):317-327.
[9] Shaw H, Lancasterjones E. Application of the Eötvös Torsion Balance to the Investigation of Local Gravitational Fields[J].QualityAssuranceinEducation, 1922, 22(1):88-104.

