基于外差激光干涉法的三轴向振动绝对校准方法研究

杨 明, 蔡晨光, 刘志华, 王 颖

(1. 北京化工大学, 北京 100029; 2. 中国计量科学研究院, 北京 100029)

1 引 言

三轴向加速度计广泛应用于航空航天、地震监测、汽车制造等领域的振动测量[1～3]。振动校准是确保加速度计测量振动有效性的前提,三轴向振动校准用于三轴向加速度计、多分量地震计等的校准,是当前的研究热点。由于外差式激光干涉仪具有位移测量精度高、噪声小、动态范围宽、线性度高等优势[4,5],外差激光干涉法被广泛应用于振动绝对校准。当前主流的三轴向加速度计振动校准方法利用单轴向振动激励依次实现其3个轴向灵敏度的校准,但整个校准过程需要多次重复安装,且对于横向灵敏度的校准,需要不断改变加速度计安装台面内的振动激励方向。重复安装不仅使得校准时间变长,而且会对横向灵敏度的校准引入较大的不确定度[7]。此外,该校准方法不适用于对加速度矢量的测量[1, 8]。Umeda A等[8]提出一种用于描述被校加速度计输入激励与其输出信号关系的灵敏度矩阵模型,并利用三轴向振动台与3个一维激光干涉仪组成的三轴向振动校准系统求解该模型,实现被校加速度计的主轴与横向灵敏度幅值的校准,整个校准过程需生成至少3次X、Y、Z向相互独立的直线运动;Usuda T等[9]利用三轴向振动校准系统,通过控制其Z轴和XY平面输出不同频率的振动,并依次改变XY平面内的振动方向实现被校加速度计横向灵敏度的校准。然而,上述校准系统中所用的激光测振方法测量的输入激励加速度存在一定的相位延时,其会引入一定的灵敏度相位校准误差。Tsuchiya T 等[10]利用3个参考加速度计实现被校三轴向加速度计输入激励加速度的测量,并通过求解动态灵敏度矩阵实现三轴向MEMS加速度计主轴与横向灵敏度幅值的校准,但其校准精度依赖于所选用的参考加速度计。

针对单轴向振动激励校准与现有三轴向振动校准方法存在的不足,本文提出一种基于带通采样的高精度外差激光干涉校准方法,并基于我国自行研制的三轴向标准振动台建立三轴向振动绝对校准系统,以同时实现被校三轴向加速度计主轴、横向灵敏度幅值与相位的校准。

2 三轴向振动绝对校准系统与原理

如图1所示,三轴向振动绝对校准系统主要包括:三轴向标准振动台,用于提供X、Y、Z方向的激励;激光测振系统,用于测量X、Y、Z方向的激励加速度;隔振系统,用于激光测振系统的隔振以保证其测振精度。被校加速度计固定于标准振动台的工作台面,利用标准振动台模拟被校加速度计的实际应用环境。

利用被校三轴向加速度计在X、Y、Z向的输入激励与其X、Y、Z轴向对应的输出信号的关系,实现被校加速度计的校准。

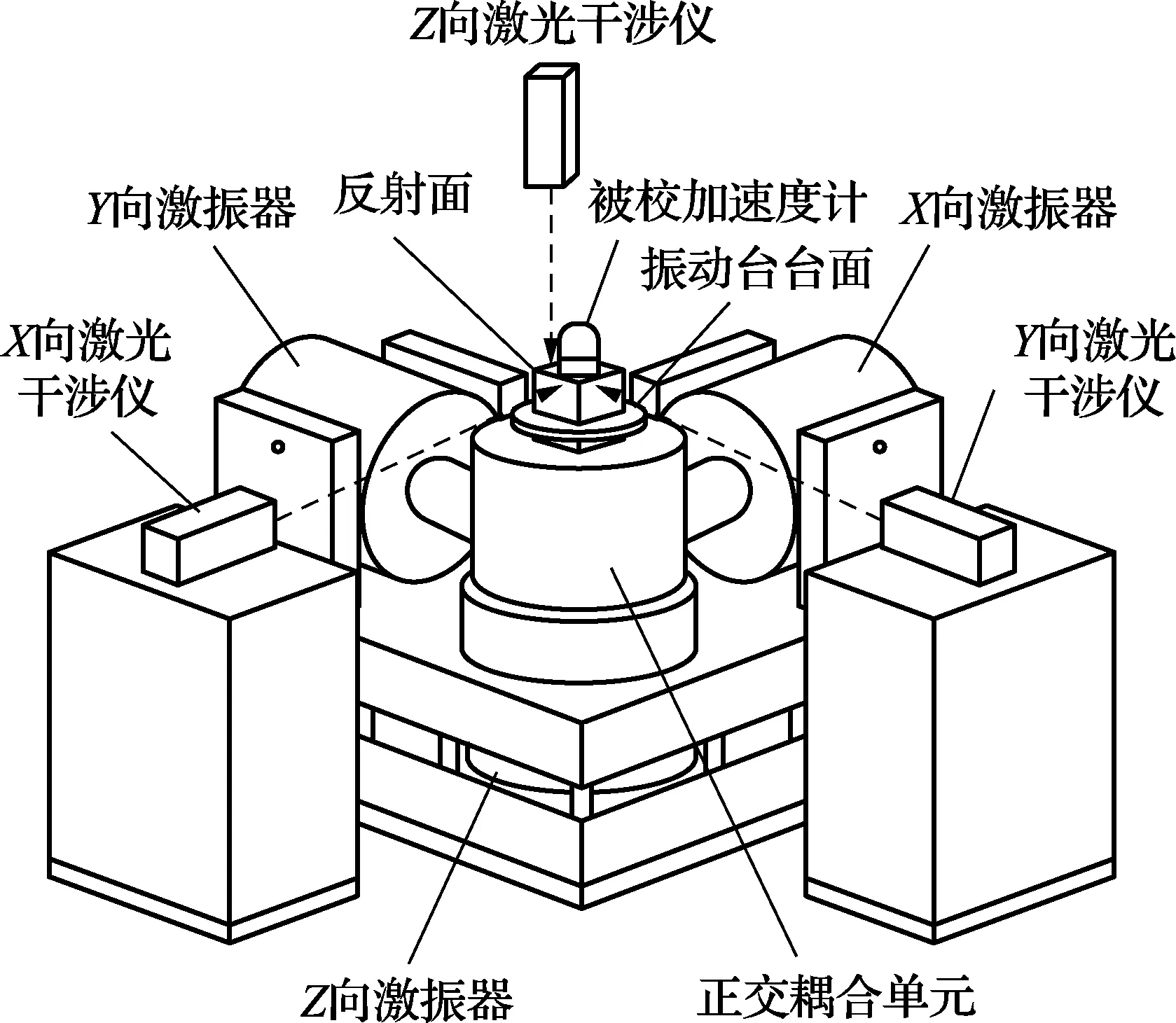
图1 三轴向振动绝对校准系统

3 三轴向振动绝对校准方法

控制三轴向标准振动台依次产生X、Y、Z向的直线运动。通过外差激光干涉法测量被校加速度计在X、Y、Z向的输入激励,并同时测量该输入激励下其X、Y、Z轴向的输出电量。利用测量的输入激励与输出电量计算被校加速度计灵敏度矩阵,进而实现其灵敏度的校准。

3.1 基于带通采样的信号采集

对于单轴向的正弦激励振动校准,其外差式激光干涉信号uL(t)[10]为

uL(t)=upcos(φ0+2 p fct+φMod(t))

(1)

其中,

(2)

式中:up,φ0与fc分别为干涉信号的峰值电压、初相与载波频率;λ为激光波长;sp、fv与φs分别为被测输入激励位移的峰值、频率与初相。

uL(t)的载波频率通常为40 MHz,远大于其带宽Bw。传统的外差式激光干涉信号采集方法主要有基于Nyquist采样定理的采集方法与使用模拟器件降频转换的采集方法。Nyquist采集方法所需采样频率高于80 MHz,需要采集与存储的数据量大。降频转换采集方法使用模拟混频器与低通滤波器降低采样频率,但会引入相位延时。由于uL(t)为高载波频率的窄带宽信号,提出基于带通采样定理的采集方法实现uL(t)的采集,所需采样频率仅与Bw有关。

为保证采集的uL(t)频谱不会混叠,即uL(t)的正、负频谱经频谱搬移后的频谱复制间不存在任何重叠,采样频率Fs需满足[11,12]:

(3)

其中m为不大于(fc+B/2)/B-1的非负整数。

满足式(3)的采样频率为有效采样频率,其在理想条件下均能实现uL(t)的无混叠采集。然而,实际的uL(t)受到外部环境振动与干涉仪光电元件非线性的影响,使用上述有效采样频率仍可能导致频谱混叠。因此,需要引入恰当的保护带宽,以保证采集频谱的工程裕差。

为避免采集实际uL(t)的频谱混叠,且同时保证uL(t)的采集精度,引入的保护带宽[11]为

BGT=BGL+BGU

(4)

其中:BGT为总保护带宽;BGU与BGL为上、下限保护带宽。m的可允许有效采样频率范围为

(Fs,max-Fs)+(Fs-Fs,min)

(5)

式中:fs,max与Fs,min分别为理论最大与最小有效采样频率。由于奇、偶数m的采样频率的采集频谱排列不同[13],且该排列影响uL(t)的采集精度,则最终的采样频率Fs,opt为

(6)

式中:BGU，max与BGL,max为m对应采样频率范围内的最大上、下限保护带宽。

3.2 输入激励加速度与输出电量测量

利用Fs,opt实现uL(t)与被校加速度计的输出电量V(t)的采集。为从采集的外差式激光干涉信号uL(ti)中获取相位φMod(ti),需先利用一组标准正余弦正交基实现uL(ti)的正交化,再经数字低通滤波,得到两路相互正交的信号:

(7)

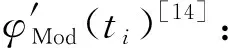
(8)

式中:kp 为避免反正切函数在正交信号的过零点处产生的不连续而引入的补偿相位,k=0,1,2,…。

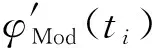
CLti+DL

(9)

式中: i=0,1,…,N-1为采样点数;ω=2 p fv为振动角频率。

求解由公式(9)的N个方程构成的超定方程组,得到参数AL与BL,CL与DL。则被测输入激励位移s(ti)为

(10)

进而得到输入激励加速度a(ti)为

(11)

使用正弦逼近法拟合采集的被校加速度计输出电量V(ti):

V(ti)=Ascos(ωti)-Bssin(ωti)+Csti+Ds

(12)

则其输出电量V(ti)为

(13)

3.3 三轴向加速度计的灵敏度矩阵

被校三轴向加速度计的灵敏度矩阵定义[7]为

(14)

式中:Sxx、Sxy与Sxz,Syz、Syy与Syz,Szx、Szy与Szz分别为其X、Y、Z轴向的主轴及相应的横向灵敏度。

为求解式(14)的灵敏度矩阵S,振动台需要沿X、Y、Z向生成独立的直线运动。利用外差激光干涉法测量得到沿X、Y、Z向的3次独立运动下的输入激励加速度axx、axy与axz,ayx、ayy与ayz,azx、azy与azz。

同时测量该输入激励加速度下的被校加速度计X、Y、Z轴向的输出电量Vxx、Vxy与Vxz,Vyx、Vyy与Vyz,Vzx、Vzy与Vzz。则S元素的求解如下:

AtriStri=Vtri

(15)

其中,Atri、Stri与Vtri分别为

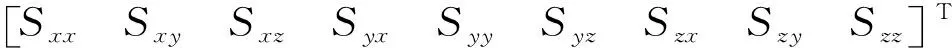
实际上,振动台沿X、Y、Z的任一方向移动时,被校加速度计在X、Y、Z向的输入激励加速度及其X、Y、Z轴向的输出电量为复数,输入激励加速度ac(ti)与输出电量Vc(ti)为

(16)

即,

(17)

利用公式(16)与(17)将公式(15)转化为

(18)

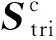
4 三轴向振动绝对校准结果验证与分析

图2为三轴向振动绝对校准装置。该装置主要包括:5～2 000 Hz频率的三轴向标准振动台、3个外差式激光干涉仪、3个隔振平台、三轴向振动控制系统及振动校准数据处理系统。利用该校准装置实现5～1 600 Hz范围内的三轴向加速度计校准,整个校准过程中被校加速度计仅安装一次,外差式激光干涉信号的采样频率约为5 MHz。

图2 三轴向振动绝对校准装置

振动频率为80 Hz时,被校三轴向加速度计在X、Y、Z向的输入激励加速度及其X、Y、Z轴向的输出电压测量结果如图3所示。

被校三轴向加速度计的灵敏度校准结果如图4所示。

实验结果验证了本文提出基于外差激光干涉法的三轴向振动绝对校准的有效性,提出的三轴向振动绝对校准方法在一定程度上很好地补充与扩展了现有的振动绝对校准方法。

5 结 论

本文提出的三轴向振动绝对校准方法能够同时实现三轴向加速度计主轴与横向灵敏度幅值与相位的高精度校准。通过带通采样方法有效采集外差式激光干涉信号,以保证激光干涉法的测振精度。被校三轴向加速度计在校准过程中仅需一次安装即可准确实现其主轴与横向灵敏度的校准,有效地避免了重复安装引入的校准误差,且缩短了校准时间。

图3 振动频率为80 Hz时被校加速度计输入与输出

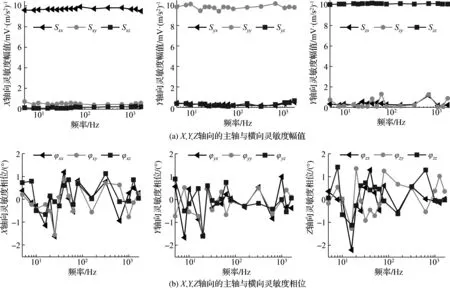
图4 被校三轴向加速度计的主轴与横向灵敏度校准结果

此外,三轴向标准振动台的振动性能会影响校准精度,以被校加速度计X轴向的灵敏度校准进行分析,振动台沿X向直线运动时,Y、Z向不可能控制到绝对零运动,其会引入X轴向横向灵敏度的校准不确定度。

[参考文献]

[1] 于梅. 三轴向振动加速度校准系统的研究[J]. 计量学报, 2010, 31(6): 517-519.

[2] Tsuchiya T, Tabata O, Umeda A. Dynamic sensitivity matrix measurement for single-mass SOI 3-axis accelerometer[C]// IEEE, International Conference on MICRO Electro Mechanical Systems. IEEE, 2012: 420-423.

[3] 何懿才, 廖建平, 赵君辙. 数学摆台法的超低频加速度校准[J]. 计量学报, 2017, 38(4): 424-428.

[4] ISO 16063-11, Methods for the calibration of vibration and shock transducers-Part 11: Primary vibration calibration by laser interferometry[S]. 1999.

[5] 于梅, 孙桥. 外差式激光干涉仪应用于正弦直线和旋转振动测量技术的研究[J]. 计量学报, 2005, 26(3): 237-241.

[6] 王月兵, 孙旭鹏, 姚磊, 等. 激光测振仪校准方法研究进展与评述[J]. 中国计量学院学报, 2015, 26(4): 399-405.

[7] ISO/DIS 16063-31, Methods for the calibration of vibration and shock transducers-Part 31: Testing of transverse vibration sensitivity [S]. 2009.

[8] Umeda A, Onoe M, Sakata K,etal. Calibration of three-axis accelerometers using a three-dimensional vibration generator and three laser interferometers[J].Sensors&ActuatorsAPhysical, 2004, 114(1): 93-101.

[9] Usuda T, Weißenborn C, Von Martens H. Theoretical and experimental investigation of transverse sensitivity of accelerometers under multiaxial excitation[J].MeasurementScience&Technology, 2004, 15(5): 896-904.

[10] Tsuchiya T, Tabata O, Umeda A. Dynamic sensitivity matrix measurement for single-mass SOI 3-axis accelerometer [C]// IEEE, International Conference on MICRO Electro Mechanical Systems. IEEE, 2012: 420-423.

[11] SUN Q, Bruns T, Täubner A,etal. Modifications of the sine-approximation method for primary vibration calibration by heterodyne interferometry[J].Metrologia, 2009, 46(6): 646-654.

[12] Betta G, Capriglione D, Ferrigno L,etal. Innovative methods for the selection of bandpass sampling rate in cost-effective RF measurement instruments[J].Measurement, 2010, 43(8): 985-993.

[13] Boute R. The Geometry of Bandpass Sampling: A Simple and Safe Approach[J].IEEESignalProcessingMagazine, 2012, 29(4): 90-96.

[14] LIU J H, ZHOU X Y, PENG Y G. Spectral arrangement and other topics in first-order bandpass sampling theory[J].IEEETransactionsonSignalProcessing, 2001, 49(6): 1260-1263.

[15] YANG P, XING G Z, HE L B. Calibration of high-frequency hydrophone up to 40 MHz by heterodyne interferometer[J].Ultrasonics, 2014, 54(1): 402-407.

[16] ISO 16063-41, Methods for the calibration of vibration and shock transducers: Part 41: Calibration of laser vibrometers[S]. 2011.