复合材料胶层光纤布格光栅应变监测优化配置研究
张玉燕, 任天昕, 温银堂, 刘 勇, 刘泽良
(1. 燕山大学 测试计量技术及仪器河北省重点实验室, 河北 秦皇岛 066004;2. 燕山大学 国防科学技术学院, 河北 秦皇岛 066004;3. 燕山大学 建筑工程与力学学院, 河北 秦皇岛 066004)
1 引 言
近年来,新型高性能复合材料以耐高温、抗氧化、抗烧蚀等优点逐渐成为新一代航空、航天器的高温热结构材料[1]。目前通常采用胶接技术和工艺将航天器热防护用复合材料粘贴在基体上[2],但粘接工艺、材料特性和服役环境等因素很大程度上影响粘接质量,决定着材料构件的防护性能和安全性能[3],因此采用准确、可靠的传感技术对复合材料结构及胶接质量进行健康监测十分重要。目前用于复合材料缺陷检测手段主要有:空气耦合超声技术[4]、散斑干涉技术[5]、太赫兹技术[6]、红外热像技术[7]、激光超声检测技术[8]等。这些检测方法各有优缺点,在进行复合材料及结构缺陷检测时通常能取得较好效果。但航空器基体热防护用C/SiC复合材料的胶接层缺陷/损伤检测仍处于探索阶段。而光纤布拉格光栅(fiber Bragg grating, FBG)传感器具有体积小、重量轻、检测灵敏度高、复用能力强、抗电磁干扰、易于嵌入材料内部[9,10]的特点,广泛应用于航空航天领域的结构健康监测。
文献[11]采用光纤布拉格光栅传感器测量结构应变场分布,对大型碳纤维复合材料机翼盒段壁板结构进行损伤监测研究。文献[12]通过FBG传感器对机翼前缘及机身部分碳纤维增强热塑性材料内部脱层、开裂等进行监测,并实现损伤定位。文献[13] 对飞行器表面低速冲击进行损伤识别研究,将FBG传感器埋入复合材料结构以实现低速冲击定位检测。由于航空部件的应变场分布与其结构形状、材料及承载等因素有关,因此必须根据航空结构的形状和材料属性特点对FBG传感器进行优化配置。文献[14]采用遗传算法给定埋入纤维增强复合材料结构传感器网络的最佳传感器布置位置。文献[15]和文献[16]通过仿真对比的方法,分析了粒子群算法应用于FBG传感器优化配置的可行性。目前将FBG传感器网络应用于复合材料结构胶层缺陷/损伤监测是一种新的胶层结构健康监测手段,埋入胶层后FBG传感器自身应变传递特性和敏感范围还有待深入的实验研究,FBG传感器网络优化配置仍缺少结合被测结构性能和FBG传感器本身结构特点的方法。
本文提出一种基于FBG应变监测的航天器基体热防护材料结构胶层缺陷/损伤检测的方法,将FBG传感器埋入C/SiC复合材料粘接胶层内部,构成分布式传感网络,并对FBG传感器的敏感范围及网络优化布置方法进行了研究,以提高FBG传感器网络覆盖率,实现高精度缺陷检测。
2 基于有限元分析的感知模型构建
FBG传感器埋入被监测结构,其性能和传感精度会受结构材料特性的影响。因此,应根据被测结构和材料,首先确定FBG传感器的应变传递特性和敏感范围,建立感知模型。基本感知模型类型有:二进制感知模型、指数感知模型和概率感知模型,其中概率感知模型基于传感器收集信号的概率表示其感知到物理信息的置信水平。本文采用该感知模型进行FBG传感器的模型构建。
目前,在对FBG传感器优化配置时通常将其敏感范围视为圆形。但FBG传感器具有轴向敏感性,若埋入复合材料粘接胶层结构,其在各个方向相等应力作用下产生的波长漂移不同,因此不能将其敏感范围视为圆形。本文采用有限元分析方法建立实体模型,进行力学分析,以确定FBG传感器的敏感范围。采用ANSYS软件建模,传感器各部分均采用8节点三维实体单元Solid185,各组成部分的几何参数及力学参数如表1所示。

表1 实验材料有限元模型参数取值表
建立的仿真模型FBG传感器长10 mm,嵌入胶层中间位置,胶层粘接在玻璃纤维复合材料基板上。
将被测基体玻璃纤维复合材料板四边简支,在胶层上表面施加垂直于胶层上表面的集中力载荷,求解光纤光栅传感器平均应变值,不同加载位置的光纤光栅段的平均应变分布如图1所示。

图1 不同加载位置的光纤光栅段的平均应变分布图
根据有限元分析可知,在微力作用下,传感器的应变变化量在με量级,在系统可测范围内;由于垂直集中载荷作用于胶层上表面,导致被测结构变形并传递给胶层内部的光纤光栅,FBG轴向受到应力作用使光栅栅距发生变化,横向应力作用于FBG时使光纤直径发生微量变化,集中力越接近光纤光栅传感器,其产生的应变越大,且在光纤光栅附近一定范围内呈现良好的检测灵敏度;当力垂直加载在光纤正上方时,FBG受到应力增大,其平均应变值有较大突变;埋入式光纤光栅传感器敏感范围呈近似椭圆形分布。
根据概率感知模型建立FBG传感器应变敏感模型特征,如图2所示。集中力载荷作用于长轴a2、短轴b2的小椭圆范围内,引起FBG传感器发生相对较大应变,认为覆盖率为1,即此范围内所有信号源产生的信号FBG传感器均可有效检测;集中力载荷作用于长轴a1,短轴b1的小椭圆范围意外区域,引起FBG传感器发生微小应变,认为覆盖率为0,即该范围内信号源产生的信号无法被检测;集中力载荷作用于两椭圆之间时,覆盖率以一定的规律由1向0逐渐减小。
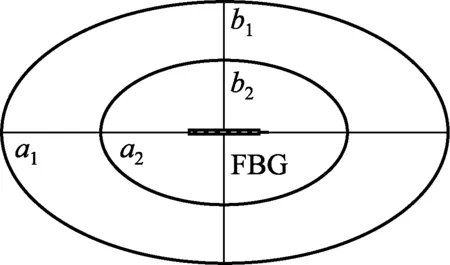
图2 FBG传感器敏感区域示意图
3 FBG传感器敏感区域探测
针对航天器基体热防护材料的粘接构件,搭建FBG传感器静载条件下应变监测系统平台,对埋入胶粘层的FBG敏感模型进行实验研究。该系统由FBG传感器、静载加载装置、静态解调系统和PC机组成,实验对象为(C/SiC复合材料)防护材料、(环氧树脂胶)胶层。光纤光栅传感器结构尺寸同ANSYS仿真结构相同,实验装置如图3所示。
为考查静载条件下胶层内部FBG传感器的应变敏感范围开展实验,所制作的试件结构参数如下:复合材料尺寸为400 mm×400 mm×25 mm;将中心波长1 551.3 nm的FBG传感器埋入胶层,胶层厚度1 mm。在胶接平面内,以FBG传感器中心为原点,以传感器轴向为x轴、径向为y轴建立坐标系,由于FBG传感器的结构对称性,只需要测量第一象限。在第一象限划分边长10 mm网格,在网格点依次施加5 N静载荷,不同加载位置造成的传感器布拉格波长漂移如图4所示。

图3 实验装置

图4 载荷加载位置与传感器布拉格波长漂移关系图
分析实验结果可知,胶层内部的FBG传感器探测范围敏感特性为:在长半轴a2=51.032 mm,短半轴b2=29.830 mm的椭圆范围内测得载荷和波长漂移关系大于2.0 pm/N,此范围内所有信号源产生的信号FBG传感器均可有效检测,认为其覆盖率为1;在长半轴a1=101.961 mm,短半轴b1=60.272 mm的椭圆范围以外测得载荷和波长漂移关系小于1.0 pm/N,此范围内信号源产生的信号FBG传感器不能辨识,认为覆盖率为0;在两椭圆之间区域时,感知概率服从某一从1逐渐减小为0的概率分布。
研究当信号源位于小椭圆外部、大椭圆内部时的感知概率分布规律,对该区域范围内长轴数据归一化并进行曲线拟合,得到敏感区内FBG传感器的覆盖率分布规律与从距离的二次方成正比例,如图5所示。

图5 波长漂移拟合曲线
设FBG传感器敏感区域模型数学表达式为
(1)
式中:(x,y)为信号源的位置坐标;D为信号源与FBG传感器的相对距离。位置坐标为(m,n)的FBG传感器与信号源相对距离D为
(2)
式中cmn为以传感器中心信号源所在位置与敏感区域椭圆相似的椭圆的焦距。如果敏感区域椭圆长半轴为a、短半轴为b,则:
(3)
4 FBG传感器网络优化配置
大量埋入FBG传感器会对材料强度造成不利影响,因此必须对FBG传感器测点位置进行合理配置,以达到或接近FBG传感器的最优分布,获得更多的结构内部有效信息。
采用N个传感器节点同时测量某一信号源,N个传感器覆盖率的联合概率为
(4)
此时,传感器优化配置效果可用传感器网络对结构上所有信号源覆盖率的最大化来评价[15]。则N个传感器对M个信号源的覆盖率为
(5)
优化传感器布置位置使得式(5)值达到最大,即得到传感器的最佳布局。
本文采用粒子群算法对FBG传感网络进行优化配置。基于实验获得的FBG传感器敏感区域模型,建立传感器覆盖优化配置模型结构。在划分40×40的网格的正方形内区域中布置32个FBG传感器,信号源位于网格节点上。每个FBG传感器敏感区域模型参照公式(1),其中a2=5.1个网格单位,b2=3.0个网格单位;a1=10.2个网格单位,b1=6.0个网格单位。
用粒子群算法在40×40网格中布置32个传感器,将FBG传感器以合适的位置配置在平板上,以式(5)作为适应度值。首先初始化粒子;通过迭代找到粒子本身的最优的适应度值和整个全局的最优适应度值;粒子在每次迭代过程中跟踪两个最优适应度值进行更新,让适应度的值达到最大,即使传感器的联合覆盖率最大。设定迭代次数为1 000次,仿真结果如图6所示。经粒子群算法计算,适应度的值可达0.998 7,即经过优化配置传感器的联合覆盖率可达99.87%。
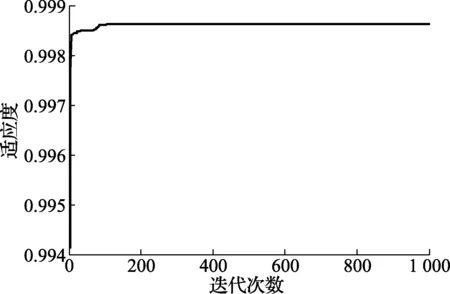
图6 适应度迭代过程曲线
考虑实际结构特点,为减少FBG传感器对粘接强度的影响,避免交叠,使每一根光纤串联更多的FBG传感器且保持平行。在优化配置过程中,筛选种群径向坐标差值小于0.2的个体坐标进行直线拟合干预,计算得到适应度为0.998 6,FBG传感器位置坐标如图7所示。FBG传感器位置坐标经过拟合干预后能保证99.86%的覆盖率。对FBG传感器简化配置后,优化配置覆盖率略有下降,但可以最大化发挥FBG传感器效用,降低了埋入胶层内部FBG传感器对胶层的影响,也大大降低了FBG传感器布置难度。

图7 粒子群算法优化后FBG传感器位置
5 结 论
针对航空航天用C/SiC复合材料构件粘接胶层的应变监测问题,研究了FBG传感网络的优化配置方法。在静载条件下对嵌入胶层内部的FBG传感器应变敏感区域进行了实验研究,分析得到其应变敏感特性近似呈椭圆形分布,并建立相应的FBG传感器感知数学模型,有限元仿真结果与实验结果一致。
基于覆盖率最优配置准则采用粒子群优化算法进行FBG传感网络的优化布置研究,经位置优化传感器网络覆盖率明显提高。并对粒子群算法进行改进,设计一种更符合FBG传感器结构特点的传感网络的优化布置方法,FBG传感网络在保证测量精度的条件下,能够达到资源合理利用、性能优化的目的。
[参考文献]
[1] 马保全, 周正干. 航空航天复合材料结构非接触无损检测技术的进展及发展趋势[J]. 航空学报, 2014, 35(7):1787-1803.
[2] 乔海涛, 邹贤武. 碳纤维复合材料的胶接工艺与性能[J]. 宇航材料工艺, 2009, 39(1):66-69.
[3] 顾轶卓, 李敏, 李艳霞,等. 飞行器结构用复合材料制造技术与工艺理论进展[J]. 航空学报, 2015, 36(8):2773-2797.
[4] 王雪明, 谢富原, 李敏,等. 热压罐成型复合材料复杂结构对制造缺陷的影响规律[J]. 航空学报, 2009, 30(4):757-762.
[5] Farge L, Varna J, Ayadi Z. Damage characterization of a cross-ply carbon fiber/epoxy laminate by an optical measurement of the displacement field[J].CompositesScience&Technology, 2010, 70(1):94-101.
[6] 杨振刚, 刘劲松, 王可嘉. 复合材料与钢板黏合面的太赫兹无损检测[J]. 无损检测, 2014,(4):42-44.
[7] Zalameda J N, Winfree W P, Yost W T. Air coupled acoustic thermography (ACAT) inspection technique[C]// AIP Conference Proceedings. 2008:467-474.
[8] SUN G K, ZHOU Z G, LI G H,etal. Development of an optical fiber-guided robotic laser ultrasonic system for aeronautical composite structure testing[J].Optik-InternationalJournalforLightandElectronOptics, 2016, 127(12): 5135-5140.
[9] 芦吉云, 梁大开, 陆观, 等. 光纤光栅传感器在CFRP冲击载荷监测中的应用研究[J]. 计量学报, 2011, 32(2):106-109.
[10] 蔡璐璐,万玉良,吴飞. 高双折射光纤光栅扭转特性分析与应用[J]. 计量学报, 2016, 37(4): 342-346.
[11] 常琦, 袁慎芳, 周恒保. 基于LS-SVMs机翼盒段壁板损伤辨识研究[J]. 压电与声光, 2009, 31(4):489-492.
[12] Kosters E, Els T J V. Structural health monitoring and impact detection for primary aircraft structures[C]// Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 2006.
[13] Shrestha P, Kim J H, Park Y,etal. Impact localization on composite structure using FBG sensors and novel impact localization technique based on error outliers[J].CompositeStructures, 2016, 142: 263-271.
[14] Markmiller J F C, Chang F K, Markmiller J F C. Sensor Network Optimization for a Passive Sensing Impact Detection Technique[J].StructuralHealthMonitoring, 2010, 9(1):25-39.
[15] 王为, 林玉池, 沈小燕, 等. 基于自适应粒子群算法的光纤光栅传感器优化配置[J]. 天津大学学报(自然科学与工程技术版), 2010, 43(10):890-894.
[16] 伊小素, 刘佳, 叶向宇,等. 基于概率模型的光纤光栅传感网络优化布置[J]. 光电工程, 2013,(01):78-83.

