基于局部均值分解多尺度模糊熵和灰色相似关联度的滚动轴承故障诊断
孟 宗, 赵东方, 李 晶, 熊景鸣, 刘 爽
(燕山大学 河北省测试计量技术及仪器重点实验室, 河北 秦皇岛 066004)
1 引 言
滚动轴承是机械设备中最容易损坏的元件之一,其工作状态的好坏直接影响整台机械设备的工作状态,因此,对滚动轴承运行状态的故障诊断具有十分重要的意义[1,2]。滚动轴承故障诊断的关键是特征提取和故障识别[3~6]。振动信号包含丰富的故障特征信息,滚动轴承振动信号具有多载波多调制的特性,是一种多分量的复杂调幅-调频信号。局部均值分解(local mean decomposition,LMD)是Smith提出的一种自适应时频分析方法,它可以将复杂的多分量调幅-调频信号分解成单分量的调幅-调频信号,分解得到的乘积函数(product functions, PF)分量保持了原始信号的幅值和频率变化[7]。LMD方法由于其在处理多分量的调幅调频信号上的优势,被广泛应用于旋转机械故障诊断领域[8~12]。模糊熵是Chen等[13]提出的一种新的序列复杂度测度方法,取得了很好的测度效果[14]。郑近德等[15]将模糊熵应用于滚动轴承故障特征的提取并在模糊熵的基础上引入了尺度因子,提出了多尺度模糊熵(multi-scale fuzzy entropy,MFE),多尺度模糊熵是对时间序列在不同尺度因子下复杂性的量度。灰色关联度分析是应用灰色系统理论进行系统分析的重要方法,它根据评价因素之间发展态势的相似或相异程度来衡量因素间的接近程度[16~19]。
基于此,本文将LMD、多尺度模糊熵和灰色关联分析相结合用于滚动轴承的故障特征提取与识别诊断。首先将滚动轴承振动信号进行LMD分解,然后选取包含主要故障信息的前几个PF分量计算多尺度模糊熵作为特征向量,归一化处理后,通过计算灰色相似关联度对滚动轴承的故障类型和损伤程度进行判断,并通过实际的故障信号进行验证,证实了该方法的可行性。
2 局部均值分解
LMD将振动信号分解为一系列的PF分量,每个PF分量都是一个包络信号和一个纯调频信号相乘得到的单分量调幅-调频信号。包络信号代表了该PF分量的瞬时幅值,而PF分量的瞬时频率则可由纯调频信号通过反余弦的方式直接求出,将所有PF分量的瞬时幅值和瞬时频率组合便可以得到原始信号完整的时频分布。LMD实质上是将多分量的振动信号分解为一系列的单分量信号的解调过程,原始信号x(t)由PF分量和残余分量uk(t)重构得到:
(1)
3 多尺度模糊熵
多尺度模糊熵基于模糊熵的计算方法,用于描述时间序列在不同时间尺度上的复杂性。其计算方法如下[14]:
1) 设一离散原始时间序列[s1,s2,…,sN],首先对原始时间序列进行粗粒化变换,得到新的时间序列
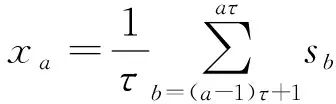
(2)
式中:1≤a≤N/τ,τ为尺度因子。当τ=1时,新的时间序列就是原始序列;
2) 确定模式维数m,进行空间重构
Xi={x(i+k)∶0≤k≤m-1}
(3)
式中:x(i+k)是xa的第i+k项。
3) 定义矢量Xi和矢量Xj间的距离dij为两矢量对应元素中差值最大的一个,记作
dij=max|x(i+k)-x(j+k)|
(4)
4) 通过混沌伪随机序列复杂度预测的模糊隶属度函数μ(x,r)来定义两矢量的相似度Dij,得
Dij=μ(dij,r)=exp[- ln 2·(dij/r)2]
(5)
5) 定义函数
(6)
6) 同理,再确定模式维数为m+1,重复步骤1)~步骤4),得到Φm+1(N,m+1,r);
7) 多尺度模糊熵定义为
(7)
N为有限值时,多尺度模糊熵表示为
FEn(N,m,r)= lnΦm- lnΦm+1
(8)
4 灰色相似关联度
传统的灰色关联度模型取值不唯一,随分辨系数的不同而发生变化,一般情况下分辨系数取0.5时,关联度值恒大于0.333。因此有必要对原有灰色关联度模型进行改进,本文引入一种新的灰色相似关联度模型来计算2个序列之间的相关程度[20]。
设X0={x0(1),x0(2),…,x0(n)}为待识别模式序列,Xi={xi(1),xi(2),…,xi(n)}(xi(k)>0,k=1,2,…,n)为参考模式序列,其中n为序列点数,i代表参考模式的种类。
令σ0,i={σ0,i(1),σ0,i(2),…,σ0,i(n)},i=1,2,…,m,其中m为参考模式种类的具体数量。则有
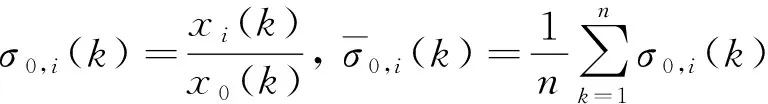
(9)
(10)

故X0与Xi的相似关联度为
(11)
相似关联度γi的大小反映了X0与Xi的关联程度,可见灰色相似关联度消除了对分辨系数的依赖,能如实地反映数据序列之间的相似程度。利用γi的大小可以对故障模式进行判断。
5 故障诊断
为了更好地进行灰色关联分析,需要对特征向量中的各个元素进行整理。对样本数据集X进行定义,设矢量X中第i个元素为X(i),这些元素中的最大值和最小值分别为Xmax,Xmin,则有:
当X(i)>Xmin时,
(12)
当X(i)=Xmin时,
(13)
由于在进行灰色关联分析时,矢量中的元素不能为0,文中取n=104。应用式(12)和式(13)对各个标准故障模式序列进行归一化处理,使之转化为(0,1]的数据。在使用经归一化处理后的标准故障进行灰色关联分析时,也需将待识别样本序列按式(12)和式(13)归一化后再进行后续分析。
基于LMD多尺度模糊熵和灰色相似关联度的故障诊断流程如图1所示。

图1 故障诊断流程图
具体步骤为:1)对滚动轴承M种状态分别进行N次采样,将得到的M×N个振动信号作为样本; 2)对每一种状态下的原始振动信号进行LMD分解,得到各个PF分量; 3)选择前n个PF分量作为研究对象,计算前n个PF分量的多尺度模糊熵; 4)构造特征向量T=[PF1(a1),…,PFn(a1),PF1(a2),…,PFn(a2),…,PF1(am),…,PFn(am)]; 5)对特征向量以及待识别的样本序列进行归一化处理; 6)计算归一化后的待识别样本与标准故障模式的灰色相似关联度,与待识别样本灰色相似关联度最大的标准故障模式的故障类型即被认为是待识别样本的故障类型。
6 实验研究
实验数据为美国西储大学电气工程实验室的滚动轴承实验数据。使用电火花加工技术在轴承上布置了单点故障,采样频率12 kHz,采样点数4 096。对不同状态下的振动信号进行LMD分解,以内圈故障信号为例,其LMD分解结果如图2所示。

图2 内圈故障信号的LMD分解
6.1 不同类型故障诊断
实验中,分别采集正常信号以及内圈故障、滚动体故障、外圈故障共4种状态的振动信号。多次采样后,从4种状态下的多组数据中每种状态各随机选取25组数据进行LMD分解,然后分别将尺度因子设定为4,8,16计算多尺度模糊熵。尺度因子为4时选取前3个PF分量,尺度因子为8和16时选取前2个PF分量,计算多尺度模糊熵作为特征向量。从每种故障类型的25组数据中各随机选取10组,分别计算相同尺度下对应PF分量的多尺度模糊熵平均值组成标准故障模式序列,共得到4组标准故障模式序列,如表1所示。将4种故障类型的各25组数据中余下的各15组共60组数据作为待测样本,分别计算与4组标准故障模式的灰色相似关联度,与待识别样本灰色相似关联度最大的标准故障模式的故障类型即被认为是待识别样本的故障类型。
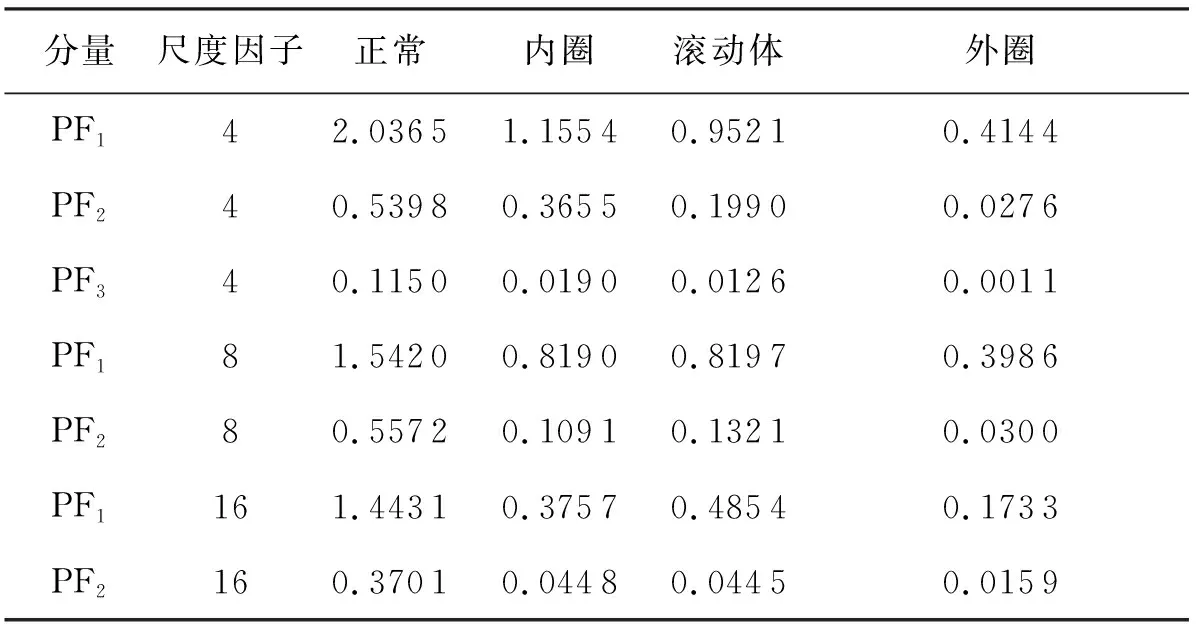
表1 标准故障模式序列
表2为待识别样本序列,其中正常状态、内圈故障、滚动体故障、外圈故障各列出一组。以正常样本和内圈故障样本为例,计算与标准故障模式序列的灰色相似关联度,结果如图3所示。

表2 待识别样本序列
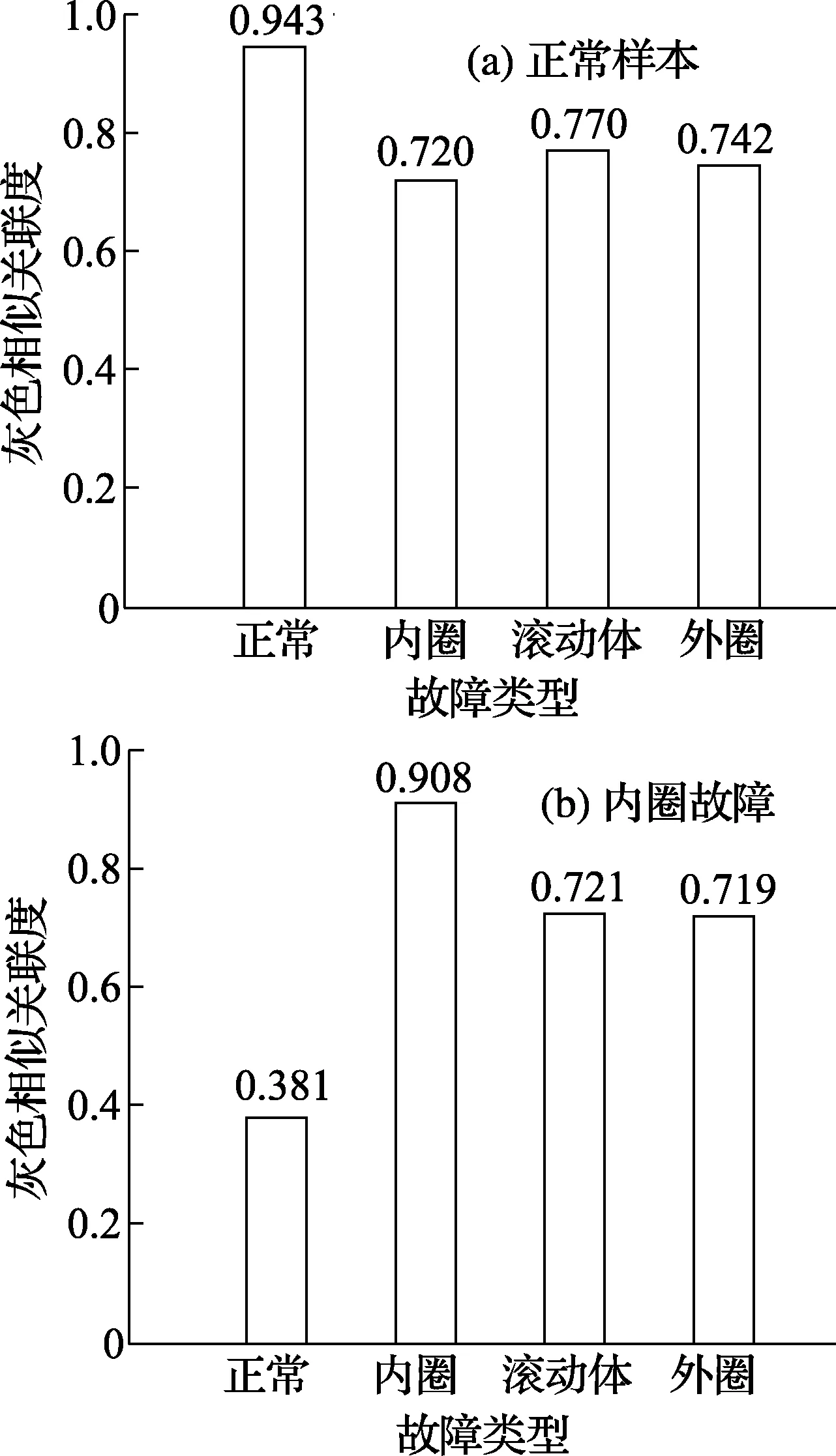
图3 不同样本与标准故障模式的灰色相似关联度
图3为不同待测样本与标准故障模式的灰色相似关联度。以图3(a)代表的正常样本为例,在与4种标准故障模式的灰色相似关联度中,与标准正常模式的灰色相似关联度最大,为0.943,表明在与4种标准故障模式序列的比较中,此样本为正常状态样本的可能性最大,故可将此样本识别为正常状态。同理,可将图3(b)识别为内圈故障。
图4为外圈故障的识别结果对比,图4(a)中虽然各样本与标准外圈故障模式的灰色相似关联度均大于与其它3种标准故障模式的灰色相似关联度,可将样本的故障类型正确识别,但与其它3种标准故障模式的灰色相似关联度区分度不高,且样本间波动较大,导致曲线相交重叠严重;图4(b)中通过计算多尺度模糊熵再通过灰色相似关联度识别,各样本与标准外圈故障模式的灰色相似关联度依然明显高于与其它3种标准故障模式的灰色相似关联度,且与其它3种标准故障模式的灰色相似关联度均被降低并且可以被较好地区分,相比图4(a)样本间的波动有所减小,曲线层次性更强,可信度更高。

图4 外圈故障识别结果对比
图5为滚动体故障的识别结果对比,由图5(a)可见,除与标准外圈故障模式的灰色相似关联度变化较平稳外,各样本与其它3种标准故障模式的灰色相似关联度虽有一定的区分度,但样本间波动较大,而且与标准滚动体故障模式的灰色相似关联度有6处低于与标准外圈故障模式的灰色相似关联度,导致识别出现错误。
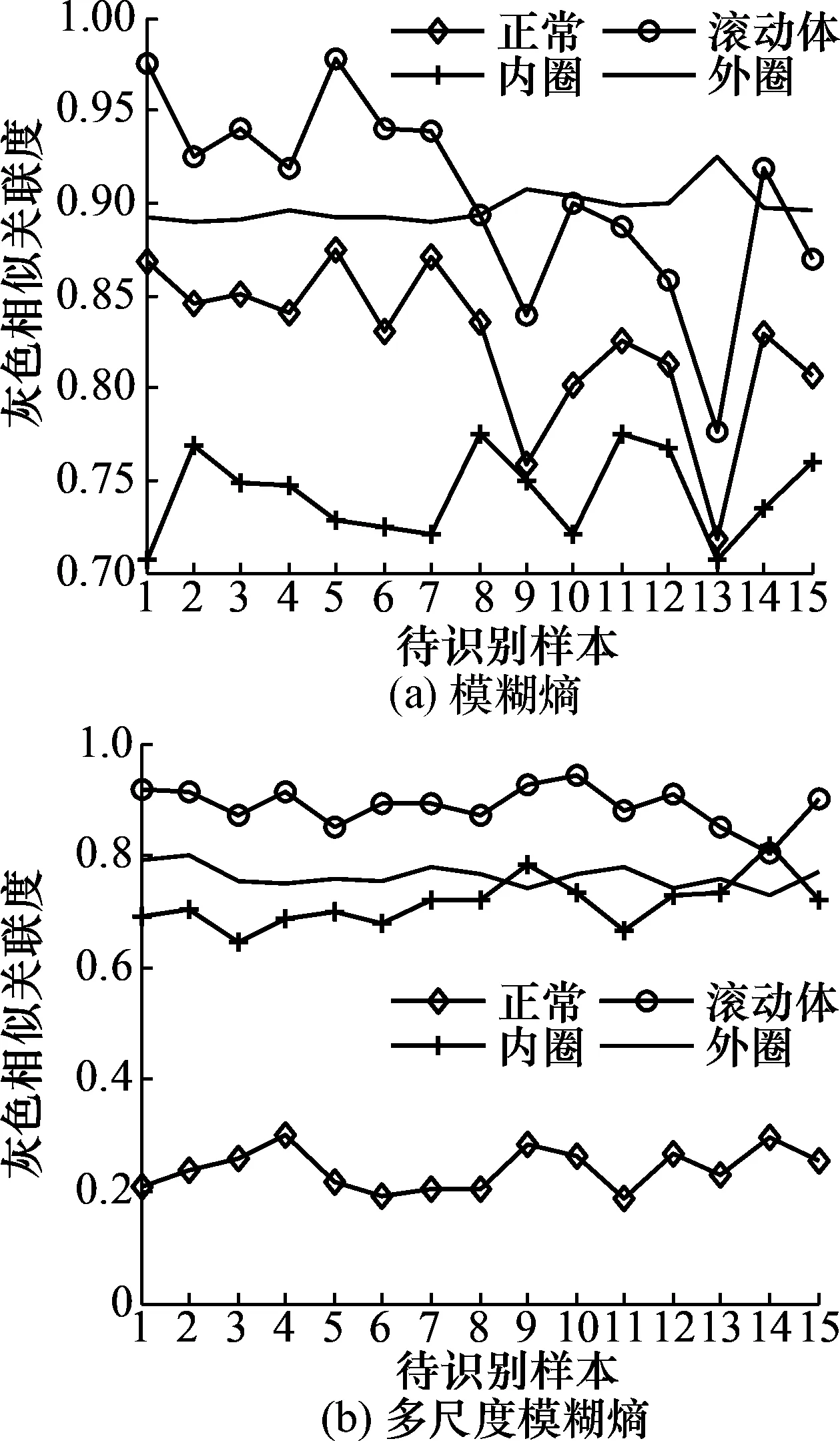
图5 滚动体故障识别结果对比
相比图5(a)与图5(b),通过计算多尺度模糊熵再通过灰色相似关联度进行识别,与4种标准故障模式的灰色相似关联度被更明显地区分,且各样本间的波动都有所减小,尤其是与标准滚动体故障的灰色相似关联度被限制在了一个较小的波动区间,而且与标准正常模式的灰色相似关联度被显著减低,提高了识别的正确率。将此方法与模糊熵和灰色相似关联度相结合的方法进行对比,结果如表3所示。
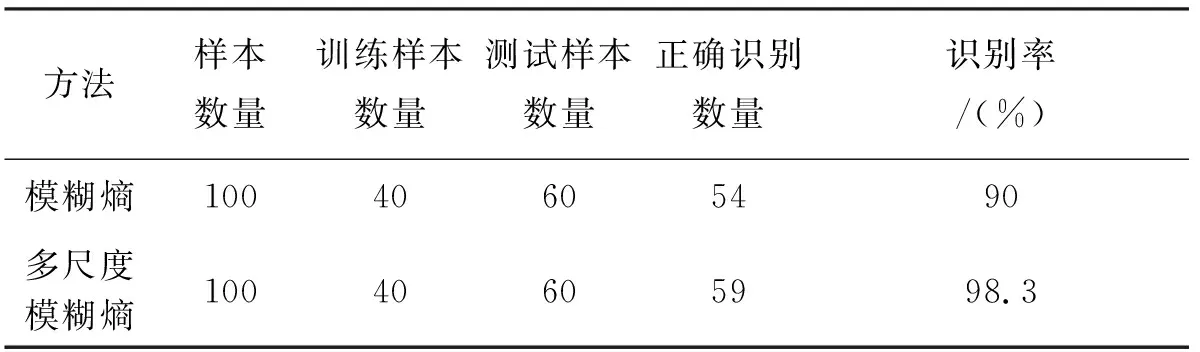
表3 故障类型识别结果正确率比较
6.2 不同损伤程度故障诊断
为进一步验证该方法在滚动轴承故障诊断中的有效性,对不同损伤程度的外圈信号进行了实验验证。在试验中,包含正常、轻度损伤、中度损伤和重度损伤4种损伤程度,其中轻度损伤故障的损伤直径为0.177 8 mm,中度损伤故障的损伤直径为0.355 6 mm,重度损伤故障的损伤直径为0.533 4 mm。
从4种状态下的多组数据中每种状态各随机选取25组数据进行LMD分解,然后分别将尺度因子设定为4、8、16计算多尺度模糊熵,尺度因子为4时选取前3个PF分量,尺度因子为8和16时选取前2个PF分量,计算多尺度模糊熵作为特征向量。从每种故障类型的25组数据中各随机选取10组共40组数据,计算相同尺度下对应PF分量的多尺度模糊熵的平均值组成标准故障模式序列,共得到4组标准故障模式序列。将每种故障程度各25组数据中余下的各15组共60组数据作为待测样本,分别计算与4组标准故障模式的灰色相似关联度,与待识别样本灰色相似关联度最大的标准故障模的故障程度式即被认为是待识别样本的故障程度。图6为中度损伤样本的分类结果对比,其中样本的损伤直径均为0.355 6 mm。

图6 中度损伤识别结果
由图6(a)可见,各样本与标准中度损伤模式的灰色相似关联度和与标准正常模式的灰色相似关联度数值差异不明显,且样本间波动较大,曲线相交重叠严重,导致识别结果失真;图6(b)通过计算多尺度模糊熵再用灰色相似关联度识别,与4种标准故障模式的灰色相似关联度被更明显地区分,尤其与标准正常模式的灰色相似关联度由之前的0.96附近降低到了0.5以下,显著提高了识别正确率。将此方法与模糊熵和灰色相似关联度相结合的方法进行对比,结果如表4所示。

表4 损伤程度识别结果正确率比较
7 结 论
提出了一种基于局部均值分解多尺度模糊熵和灰色相似关联度相结合的滚动轴承故障诊断方法。局部均值分解作为一种自适应的信号处理方法,能将复杂的非平稳信号分解为若干个PF分量;多尺度模糊熵是对模糊熵的改进,与样本熵、模糊熵相比包含更多的时间模式信息。原信号分解后所得PF分量的多尺度模糊熵能够反映信号在不同尺度的复杂性,以之构建特征向量,并通过灰色相似关联度进行状态识别和分类。实验结果表明,该方法可以对故障类型和损伤程度进行分类判断,是一种有效的故障诊断方法。
[参考文献]
[1] 王宏超, 陈进, 董广明. 基于最小熵解卷积与稀疏分解的滚动轴承微弱故障特征提取[J]. 机械工程学报, 2013, 49(1):88-94.
[3] 孟宗, 季艳, 闫晓丽. 基于DEMD和模糊熵的滚动轴承故障诊断方法研究[J]. 计量学报, 2016, 37(1):56-61.
[3] 时培明,王敬,温江涛,等. 基于包络线算法改进EMD的旋转机械故障诊断方法研究[J]. 计量学报, 2016, 37(1): 62-66.
[4] 杨宇, 李紫珠, 何知义, 等. 基于ASTFA降噪和AKVPMCD的滚动轴承故障诊断方法[J]. 中国机械工程, 2015, 26(21):2934-2940.
[5] 谢平, 江国乾, 李兴林, 等. 本征时间尺度排序熵及其在滚动轴承故障诊断中的应用[J]. 燕山大学学报, 2013, 37(2):179-184.
[6] 李巧艺, 单奇, 陈跃威. 基于HHT边际谱熵-马氏距离的滚动轴承故障诊断[J]. 燕山大学学报, 2016, 40(6):493-498.
[7] Smith J S. The Local Mean Decomposition And Its Application To EEG Perception Data[J].JournaloftheRoyalSocietyInterface, 2005, 2(5):443-454.
[8] 孟宗, 李姗姗, 王亚超. 基于LMD和局域时频熵的旋转机械故障诊断方法[J]. 计量学报, 2015, 36(1):77-81.
[9] 张立国,康乐,金梅,等. 一种基于EEMD-SVD和FCM的轴承故障诊断方法[J]. 计量学报, 2016, 37(1): 67-70.
[10] 孟宗,王晓燕,周明军,等. 基于Gabor变换和盲源分离的旋转机械故障诊断方法[J]. 计量学报, 2016, 37(5): 499-504.
[11] 王建国, 吴林峰, 秦绪华. 基于自相关分析和LMD的滚动轴承振动信号故障特征提取[J]. 中国机械工程, 2014, 25(2):186-191.
[12] CHENG J S,YANG Y,YANG Y. A Rotating Machinery Fault Diagnosis Method Based on Local Mean Decompo-sition[J].DigitalSignalProcessing,2012,22:356-366.
[13] CHEN W T, WANG Z Z, XIE H B,etal. Characterization of surface EMG signal based on fuzzy entropy[J].IEEETransactionsonNeuralSystemandRehabilitationEngineering,2007,15(2):266-272.
[14] CHEN W T,ZHUANG J,YU W X,etal.Measuring complexity using FuzzyEn,ApEn,and SampEn[J].MedicalEngineeringandPhysics, 2009, 31(1):61-68.
[15] 郑近德, 陈敏均, 程军圣, 等. 多尺度模糊熵及其在滚动轴承故障诊断中的应用[J]. 振动工程学报, 2014, 27(1):145-151.
[16] 卢绪祥, 苏一鸣, 吴家腾, 等. 基于EMD及灰色关联度的滑动轴承润滑状态故障诊断研究[J].动力工程学报,2016,36(1):42-47.
[17] LI Y P, CHEN M Y,LIU M.Estimation method for aircraft similarity based on fuzzy theory and grey incidence analysis[J].TransactionsofNanjingUniversityofAeronauticsandAstronautics, 2007, 24(3):194-198.
[18] 靳春梅, 樊灵, 邱阳, 等. 灰色理论在旋转机械故障诊断与预报中的应用[J]. 应用力学学报, 2000,17(3):74-79.
[19] 裴峻峰, 于志远, 董雪, 等. 基于LMD和灰色相似关联度的轴承故障诊断方法[J]. 机械设计与制造, 2015, (4):66-69.
[20] 张文斌, 苏艳萍, 普亚松, 等. 基于集合经验模式分解能量分布与灰色相似关联度的齿轮故障诊断[J]. 机械工程学报, 2014, 50(7):70-77.

