激光外差探测阵列互相关相干累积法
李 静,李 铁,2,李 岗,胡文惠,2,李 伟,李 抟
(1.西安机电信息技术研究所,陕西 西安 710065;2.机电动态控制重点实验室,陕西 西安 710065)
0 引言
激光外差探测作为高精度全息探测技术之一,因其高灵敏度和高光谱分辨率等众多优点被广泛应用,尤其对于复杂背景下远程距离微弱信号的检测,展示出直接检测所无可比拟的优势[1]。外差效率是评价外差技术性能的重要指标。要获得高的外差效率,波束必须保证严格的空间相位对齐。然而当激光照射到光学粗糙表面上形成散斑场时,光电探测器表面的本振光和接收到的信号光会发生波前不匹配,从而使得光敏面上不同面元输出的有用中频信号由于随机相位的波动而互相抵消,最终导致外差探测系统的性能明显下降,这就是退相干效应。
粗糙目标对光外差信号产生的退相干效应,仍然是制约主动光外差检测技术工程化应用的一个核心问题。文献[2]指出了用阵列探测器代替单探测器来提高外差检测的性能是可能的。假设阵列中每个探测器单元的输出进行相移并相加,外差效率就会得到提高。但是,如何确定阵列单元的相位调整量,特别是如何用阵列探测器校正相位失配,没有更多的研究。
本文旨在给出一种低信噪比条件下,外差信号相位测量的有效方法。利用互相关方法来确定探测器单元输出的每个序列的移动步长,将移位步长视为离散变量,以外差探测信号在累积结果中的频谱幅值作为目标方程。按照这一思路,阵列单元信号间相位差的解算问题可以转化为连续离散阵列信号累加后目标函数求极值的组合优化问题,其相位信息由对应的最优移位步长来决定。
1 光外差探测原理及模型
1.1 光外差探测原理
光外差探测是基于信号光和本振光在光电探测器光敏面产生的相干效应,可以获取振幅、频率及相位信号[3]。激光器发出的激光被分束器分为两路信息,微弱信号和强本振信号在探测器的光敏面上发生混频,探测器最终接收中频范围的信号。图1所示为激光外差原理图。
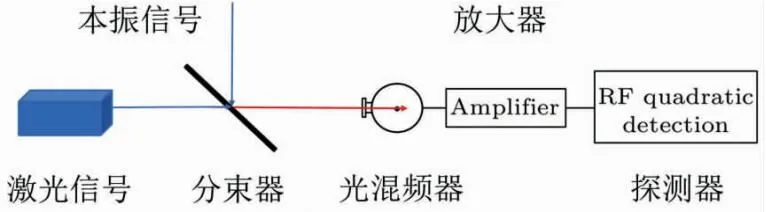
图1 激光外差原理图Fig.1 Schematic diagram of laser heterodyne
假设本振光和信号光均是线性极化的平面波,因此,电场信号可以被描述为
EL(t)=ELcos(ωLt+φL),
(1)
ES(t)=EScos[ωSt+φS],
(2)
式中:φL和φS分别为恒定相位。两束光叠加在量子效率为α的探测器光敏面上的输出电流为
(3)
将式(1)和式(2)代入式(3)可得
(4)
由于探测器带宽的限制,最终输出的仅有第三项差频项ωIF=ωS-ωL。
i(t)=αESEL[cosωIFt+(φS-φL)]。
(5)
根据式(5)可以发现,利用光外差探测,振幅调制ES、频率调制ωS=ωIF+ωL、相位φS携带信息都可以检测出来。
1.2 粗糙目标退相干效应的产生机理
激光照射目标后,部分光被散射并返回接收器,与外差接收器中的本振光耦合。通常情况下,信号光的相位和振幅都是由粗糙目标表面调制产生的,且相位调制对外差性能的影响远大于振幅调制。
探测器敏感区附近的电场信号可以描述为
EL(t)=ELcos(ωLt+φL),
(6)
ES(t)=EScos[ωSt+φS+φ(r)],
(7)
式中:φ(r)是粗糙表面的调制相位。探测器输出的电流信号为
(8)
由于粗糙平面的影响,探测器不同元件产生的中频信号会基于随机相位的波动而相互抵消,即式(8)中被积函数互相抵消为零。为了解决退相干效应引起的外差信号性能恶化,关键是消除φ(r)扰动对中频信号的影响。
1.3 粗糙目标回波信号模型
为解决粗糙目标导致的退相干效应,首先从散斑场可视化建模的角度出发。本文采用蒙特卡洛方法,并基于相关统计参数进行特性分析,从而构建粗糙目标回波信号模型。
首先假设波长λ为1 μm,探测器的边长尺寸是0.6 mm,在一个波长上取3个采样点,就可以将随机散斑场用一个1 800×1 800的矩阵来描述。高斯随机散斑场中二维粗糙面对应的功率谱[4]:
(9)
式中:δ为描述随机粗糙表面的高度起伏均方根,clx和cly为相关长度。
图2是利用统计蒙特卡洛方法描述二维随机粗糙面的模拟图。观察图2可以看出,高度均方根决定相位起伏,相关长度决定了相位起伏的变化程度。该结果可以为研究粗糙目标导致的空间相位起伏提供重要依据。

图2 统计蒙特卡洛方法描述二维随机粗糙面的模拟图Fig.2 Simulation of two-dimensional random rough surface described by statistical Monte Carlo method
2 阵列信号相位补偿方法
基于阵列的空间相位起伏补偿的过程本质是完成所有探测器单元输出信号的等相位叠加。实际上,确定阵列探测器的移相量可以看作是一个信号相干叠加求极大值的组合优化问题。
2.1 序列移位理论
当对随机相位进行补偿之后,将数字外差信号累加可获得最大强度[5-6]。在最大值存在的情况下,可由对应的最佳移动步骤决定相位信息。
针对粗糙目标,相位起伏的变化是不确定的。第m行第n列阵列探测器输出的外差信号:
(10)
式中:φmn是阵列单元信号输出的随机相位。考虑噪声对输出信号的影响:
(11)

外差信号的第k个采样为
(12)

(13)
式中:kmn=k+lmn,lmn是第m行第n列个信号的移位步长。

(14)
式中:Δφ=wIFΔt是两个相邻采样之间的相位差。
当lmn满足以下方程:
φ11+l11Δφ=φij+lijΔφ=φmn+lmnΔφ,
(15)
即可在一定程度上进行补偿,从而实现近似等相位叠加,其中lmn是最优移位步长。以φ11为参考相位,根据转移步长可获得Δφ的值。
Δφmn,11=φmn-φ11=(l11-lmn)Δφ。
(16)
2.2 目标函数模型的建立
为求解组合最优化的极值问题,设定目标函数,经相位补偿后的输出总信号可以表示为
(17)
式中:kmn∈{1,2,…,100},Imn[2 000-kmn:-kmn+3 999]意味阵列信号向左偏移kmn后提取连续离散数据。
第m行和第n列的相位补偿量为
(18)
频谱分析的结果如下:

(19)
根据以上推导,设定目标函数为输出信号频谱的10 Hz外差分量。
2.3 利用互相关进行相位补偿
根据2.2节可以发现,如何找出外差信号最大值时对应的最佳移位步长,是解决退相干效应的关键。本文将移位步长视为离散变量,以外差探测信号在累积结果中的频谱幅值作为适应度。通过分析主动光外差探测机理,将互相关理论引入探测器方法中搜索最优步长,直到满足迭代终止条件。
相关分析本质是比较两个信号在时间域的相似性[7]。由于单频信号的时移可近似看为相移,通过求解互相关函数的极大值,即可准确地计算随机相位的调整量,从而实现组合最优化。
仿真时,两路时间信号序列都向中间平移,横坐标是移位步长,纵坐标是互相关函数。互相关系数取到极值的时候,说明最佳移位步长已经找到,经补偿后达到近似等相位。将φ1作为参考相位,Δφmn是阵列信号的相位差。结合式(15)测量误差可以被表示为
(20)
测量误差的值在表1中给出,结果证明互相关法具有相当高的测量精度。

表1 SNR=-10 dB的测量误差Tab.1 Measurement error of SNR=-10 dB
仿真中,外差信号频率设为10 Hz,系统数模转换器采样频率设为1 000 Hz,那么4 s以内的信号就能用4 000个离散采样点来表示。同时为了模拟粗糙探测目标引起的退相干影响,对所有探测器阵元所获信号信噪比进行了设置,分别为SNR=-3 dB,SNR=-10 dB,SNR=-17 dB,通过迭代100次寻找最优解,外差探测信号在累积结果中的10 Hz频谱幅值如图3所示。

图3 低信噪比下外差探测信号在累积结果中的10 Hz频谱幅值结果图Fig.3 The 10 Hz spectrum amplitude of heterodyne detection signal at low signal-to-noise ratio
如图3所示,经过互相关算法处理后的阵列外差信号振幅结果较高。当SNR=-17 dB时,振幅结果离散度较高。
迄今关于测量相位调整量的研究基本围绕着智能优化算法,将最优化理论引入探测器方法中,可有效提高外差系统的信噪比,例如遗传算法(GA)、粒子群算法(PSO)、蚁群算法(ACO)等[8-10]。虽然这些基于最优化理论的研究具有良好的性能,但是在低信噪比的情况下,优化算法的计算能力不足。据此,本文为了进一步验证互相关方法的优越性,对比常见的智能优化算法,并对其进行改进。其中自适应粒子群算法(APSO)是一种通过调整自适应参数来提高性能的优化方法[11];模拟退火粒子群算法(simulated annealing particle swarm optimization,SAPSO),在粒子群的基础上引入模拟退火的思想,可以有效改善粒子群算法陷入局部收敛的问题[12];自适应策略的改进粒子群算法(MPSO)是一种通过设置混沌权值并且引入自适应学习的优化算法,可有效提高收敛精度[13];基于GA_ACO_PSO(GAP)[14]的优化算法,可有效避免PSO的早熟收敛,且极大地提高收敛速度;麻雀搜寻算法(SSA)是一种较新的智慧启发算法[15]。图4是互相关法对比智能优化算法的频谱结果图。

图4 智能优化算法处理后阵列外差信号的频谱结果图Fig.4 Spectrum results of array heterodyne signal processed by intelligent optimization algorithm
为了量化分析,采用常用的统计学评价指标对外差信号的输出结果进行研究。表2中给出了SNR=-10 dB的条件下互相关和优化算法外差信号频谱分量的统计值。根据统计结果可以看出,在对相位的补偿上,互相关算法的总体表现最优。此外,在信噪比较低情况下,其测量精度也优于传统智能优化算法。

表2 SNR=-10 dB时互相关法和优化算法的外差信号频谱分量的统计分析结果Tab.2 Statistical analysis results of spectral components of heterodyne signal by cross-correlation method and optimization algorithm when SNR=-10 dB
3 仿真验证
为进一步验证理论推导和仿真分析所得的结论,基于外差探测系统的设计原理和实现方法,本文搭建光外差探测实验系统,并对该系统对实验目标进行相位补偿的性能进行了分析讨论。
实验中选用镜面合作目标作为对照组,标准表面粗糙度为0.2和0.8 μm的喷丸比较样块目标作为实验组。实验涉及到的仪器有:连续波激光器、分束器1(BS)、声光调制器(AOM)、实验目标和可移动支架、分束器2、CMOS高速摄像机,NAC推出的MEMRECAM超高性能ACS-1传感器摄像机、PC端,用以采集信号并进行数据处理。
在具体实验中,波长为532 nm的激光经分束器1分光成本振光束和信号光束,声光调制器用以调节信号的中心频率,使得探测器响应到的频率宽度约为20 kHz。通过调整分束器2使得空间光束对齐,还可以通过调整可移动支架实现光束的对齐,尽可能地保证完整的光斑信号照射到探测器表面[16]。图5为基于高速摄像机的主动外差探测实验平台。

图5 基于高速摄像机的主动外差探测实验平台Fig.5 Experimental platform of active heterodyne detection based on high-speed camera
实验操作过程中,由于激光的功率较大,通过使用光衰减片设定信号光功率是0.02 μW,本振光是1.7 mW。高速摄像机的拍摄模式是320×80@100 000 帧/s,采样图源的展示尺寸是880 μm×880 μm,图6是对照组和实验组的高速摄像机采样图源。

图6 高速摄像机的采样图源Fig.6 Sampling source of high-speed camera
从图6可以看出,镜面目标的采样图源比较完整,两种喷丸粗糙度目标的采样图源存在部分缺失,比较模糊,呈现不均匀状态。对采集得到的图样像素点之和进行频谱分析,图7为采集的信号频谱图。

图7 高速摄像机采集的信号频谱分析图Fig.7 Spectrum analysis diagram of signal collected by high-speed camera
可以看出,随着目标表面的粗糙度变大,外差探测的效率也会大大降低。以不同粗糙度的目标表面为例,基于之前理论的基础,利用互相关方法处理之后得到的归一化外差效率如图8所示。

图8 利用互相关方法处理后得到的外差效率图Fig.8 Heterodyne efficiency diagram obtained by cross-correlation method
如图8所示,经互相关方法处理后对照组的外差效率均值较高。可以看出,本方法计算之后的结果较优,且越来越接近理想值,从而证实了该方法的有效性。
4 结论
本文提出一种利用阵列探测器进行随机相位补偿的方法。基于外差信号在模数转换器相邻两样本间存在随机相位差这一事实,利用互相关方法对探测器元件输出的信号序列搜索确定最优步长位移并求和作为总输出,利用时域相位差来补偿空间相位差。从而将阵列单元信号间相位差的解算问题转化为连续离散阵列信号累加后目标函数求极值的组合优化问题。搭建光外差探测实验系统,设置光滑镜面为对照组,0.2和0.8 μm的粗糙度喷丸为实验组,对该系统对实验对象进行相位补偿的性能进行了分析讨论,验证了互相关法可有效提高光外差测量精度,且实现毫秒量级的信号处理时间。实验结果验证了理论部分和仿真分析的一致性。该研究工作为解决退相干效应问题提供了一种实用化新思想。

