最小范数约束的改进MVDR波束形成算法
李 涛,孙心毅,成建波
(中国人民解放军92728部队,上海 200436)
0 引言
自适应波束形成已广泛应用于雷达、声呐、无线通信、语音信号处理等领域[1-3]。常规波束形成性能受各种误差的影响小,具有较好的稳健性,但是其角度分辨力无法突破“瑞利限”。基于样本矩阵求逆的自适应波束形成算法可以获得高分辨波束形成,在期望信源方位形成波束增益,并在干扰方位形成零陷,其中最小方差无畸变响应(MVDR)波束形成算法即采用典型的采样矩阵求逆算法。该算法使阵列在期望方向上的信干噪比最大,而使输出功率最小,在理想条件下具有优越的性能[3-5]。但该算法在阵列流形误差、噪声功率等非理想因素均会导致MVDR自适应波束形成器性能下降,难以有效均衡和同时优化干扰和噪声抑制。为提高自适应波束形成器的稳健性,近年来各种新的算法相继提出,包括对角加载[6-7]、特征子空间投影[8-9]以及子阵预处理[10]、方差矩阵重构[11]等算法。对角加载的加载量恒定,不能适应环境的变化,且以牺牲干扰抑制性能为代价;子空间类方法由于需要进行噪声和信号子空间的判别,对先验知识的依赖性较强,对信噪比要求较高,且在阵列流形误差小时退化为MVDR算法;子阵预处理通过预处理可提高信信噪比,但会提高子阵噪声输出的相关性;方差矩阵重构对目标和干扰方向的先验信息要求较高。本文从获取线性约束最小范数解的角度,讨论MVDR波束形成算法的改进方法。
1 信号模型及MVDR算法
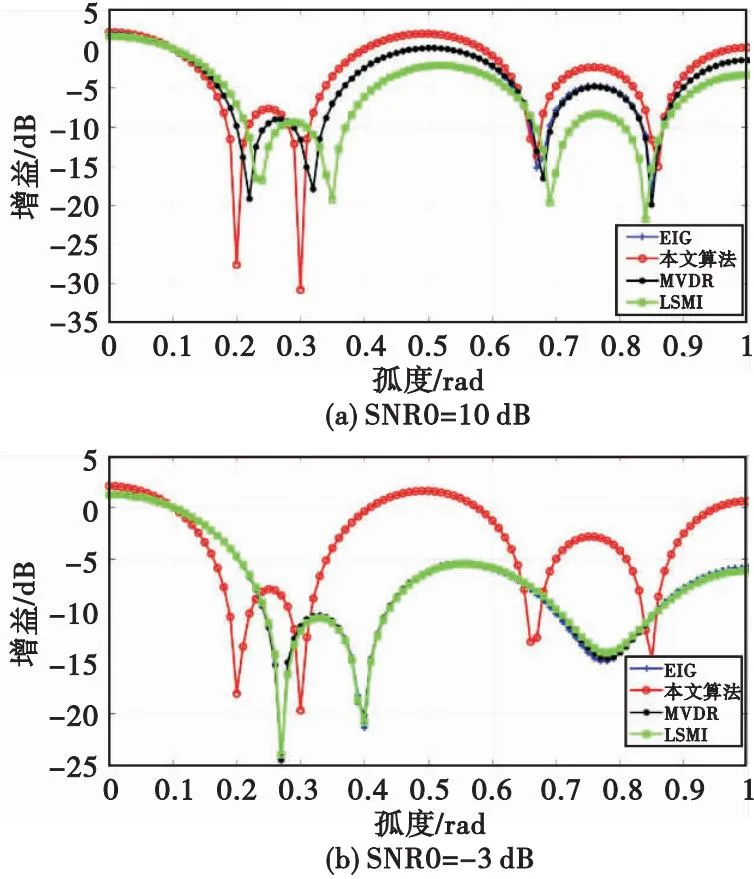
考虑一个由N个全向阵元组成的均匀线性阵列,阵列间距为d。假设M个远场窄带信号(M x(t)=[x1(t)x2(t) …xN(t)]T=A(θ)s(t)+n(t), (1) 式中:A(θ)=[a(θd)a(θ1) …a(θM-1)]为N×M维阵列流形矩阵,a(θd)和a(θi)为对应的方向向量,且有 (2) λ为信号波长,s(t)与n(t)分别为信号矢量和噪声矢量。 最小方差无失真响应(MVDR)波束形成算法通过在各阵元间附加一个权系数,使阵列在期望信号方向上的信干噪比(SINR)最大,而使输出功率最小,其原理简单,在干扰位置处能够形成零陷。MVDR权重优化问题可以表示为 (3) 式中:R=E[x(t)xH(t)]。使用拉格朗日乘数法可以得到式(3)的最优解为 (4) 为获得自相关阵R的估计,基于窄带信号的特点,R可通过时间相关过程估计,即 (5) 式中:L为样本总量。 为提高MVDR波束形成器在小样本下的稳健性,对角加载算法是在式(3)条件上增加权重向量长度的优化项,即 (6) 式中,λ为加载因子。式(7)的最优解为 (7) 考虑到信号互不相关,信号与噪声互不相关,则式x(t)的自相关阵为 (8) (9) (10) 为实现在干扰位置处能够形成零陷,关键是获得线性约束方程 wHa(θd)=1 s.t.wHa(θi)=0 (i=1,2,…,M-1), (11) 为获得最优w,将式(8)自相关阵R表示为 (12) 且 (13) (14) (15) 式中:UB=[u1u2…uM]。由式(15)获得了B的特征分解,进一步,可令A′的奇异值分解为 (16) 为构建A′的双正交基,令 (17) 显然有CHA′=I,即C与A′互为双正交基,且有 (18) 易知 A′HCCHA′=A′HDA′=I, (19) 即 则有 xH(t)Da(θd)(aH(θd)Da(θd))-1=s1(t)+ (20) 式(20)的过程实现了期望信号、干扰信号的分离,满足式(11)的条件,且由于 span(D)=span(UB)=span(A′)=span(A(θ)), 易知,取 (21) 时,w∈span[A(θ)],可取得最小范数意义上的最优解。 式(21)只是获得了信号分离意义上的最优解,为适用于波束形成,也就是抑制阵列接收信号不含期望信号,即a(θd)∉A(θ)时波束形成输出,可将式(21)表示为 (22) 其中 式(22)中,易知a(θd)∈A(θ)时,分母第二项等于0,与式(19)的结果一致;当a(θd)∉A(θ)时,由于分母第二项迅速增大,从而抑制输出,与式(4)的原理一致。 (23) 由于式(11)的条件和最小范数约束,式(22)实现了干扰信号的最优约束和以此为前提的噪声最佳抑制,由于其干扰抑制的最优性,使得其非常利于后续在时间维的滤波处理,因为此时时间维滤波处理的唯一优化目标是噪声抑制,这是容易实现的,例如窄带或者匹配滤波等,这一点将在仿真实验分析中继续说明。 仿真实验验证算法2个方面的性能,实验1验证不同信噪比下的算法性能,实验2验证不同信噪比情形下,经过波束形成后的信噪比提高性能。 实验1 设阵元个数为5,阵元间距为半波长,信号采样率为400 MHz,信号载频为55 MHz,方位为0.1π,方位误差为0.03π。2个不等功率窄带信号分别从0.2π,0.3π方向入射到阵列。图1(a)、图1(b)分别给出了信噪比为-3 dB和-31 dB时的波束形成结果。 图1 不同信噪比下的波束形成结果Fig.1 Beamforming results at different SNR 由图1的结果可以看出,采用式(22)本文算法的结果能够在干扰位置处形成零陷,较之于MVDR,LSMI和特征子空间投影(EIG)算法有更好的干扰抑制性能,这得益于其最小范数最优解的结果,但同时,由于式(22)是在取得最优干扰抑制的前提下再优化噪声抑制性能的,因此其噪声抑制效果会降低,这体现在曲线在整体上较之其他三类算法更高。但由于在抑制干扰的前提下再从时间维进行噪声抑制会更容易,因此最终会提高整体性能,这一点将在实验2中进一步试验说明。 实验2 在实验1的条件下,对波束合成输出进行时间维窄带滤波,由10 000次蒙特卡罗仿真统计期望信号信噪比。图2给出了不同阵元信噪比SNR0条件下的期望信号信噪比。 图2 不同阵元信噪比条件下期望信号信噪比Fig.2 The desired SNR at different element SNR 如图2所示,在不同阵元信噪比条件下,显示出本文算法较之MVDR,LSMI和特征子空间投影(EIG)算法具有更优良的噪声抑制性能,尤其是在阵元信噪比SNR0较低时,这同样得益于其最小范数最优解的结果。 针对MVDR算法难以有效均衡和同时优化干扰和噪声抑制的问题,提出一种基于最小范数解的改进MVDR波束形成算法。通过对阵列接收信号的自相关阵进行特征分解,取大特征值减去噪声功率及大特征值对应特征向量,构建线性约束方程的最小范数解,代替MVDR算法中的自相关阵的逆的形式形成加权系数,其中噪声功率由小特征值的平均值估计,获得的权系数对应于线性约束条件下的最小范数解。仿真分析表明,该算法能够有效地在干扰位置处形成零陷,且利于后续在时间维的噪声滤波处理,较之于MVDR等算法有更好的干扰和噪声抑制性能。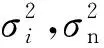

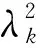
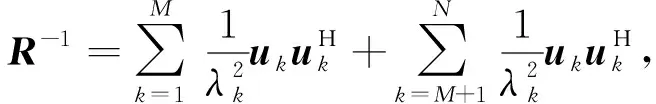
2 基于最小范数解的改进MVDR算法




n(t)Da(θd)(aH(θd)Da(θd))-1,
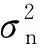

3 仿真实验及分析

4 结论

