基于漏斗函数双电机伺服系统跟踪与同步控制
张 楠 ,王树波
(1.青岛大学自动化学院,山东 青岛 266071;2.山东省工业控制技术重点实验室,山东 青岛 266071)
0 引言
双电机驱动伺服系统已在工业和军事领域得到广泛应用。电机功率需求的降低和系统设计成本的降低使多电机驱动系统越来越受到人们的重视,但由于齿隙、摩擦以及其他未知扰动的影响,会降低系统的性能甚至会导致系统运行不稳定。因此为了补偿间隙和摩擦,实现高精度的负载跟踪控制一直是伺服系统领域研究的重点和难点。国内外学者提出了许多有效的控制策略并广泛应用,如反步控制[1]、滑模变结构控制[2]、动态面控制[3],然而以上方法都是根据系统的稳态性能而进行的控制器设计,并不能限制被控系统的状态演化或跟踪误差。
规定性能控制技术[4]可以预置跟踪误差的收敛性,即在保证瞬态性能的同时不损失稳态性能,但其存在潜在的奇异性问题[5]和误差转换的复杂性。漏斗控制[6-7]由于其简单的控制结构、无记忆性和高增益特性并且可以保证跟踪误差足够小且在漏斗边界内而受到更多的关注。但漏斗控制主要适用于阶数为1或2的一类系统,限制了其在实际中的应用。
上述方法虽然提高了系统的跟踪性能,但是没有考虑到双电机伺服系统的同步问题。双电机同步运行的效果不但会影响电机的使用寿命,更会影响负载的跟踪效果。目前针对多电机同步问题,提出了交叉耦合控制[8]、相邻交叉耦合控制[9]、环形耦合控制[10]、相对耦合控制[11]等策略。然而,随着电机数量的增加,这些同步控制策略提高了控制器设计的复杂性,并且跟踪与同步之间的耦合问题可能会影响控制系统的瞬态性能。
因此,针对双电机负载跟踪这一问题,本文提出在漏斗控制中加入非光滑漏斗误差面的方法,解决传统规定性能控制存在的奇异性问题,并且能够实现高阶多电机驱动系统的全阶跟踪误差规定性能收敛。同时,为了解决双电机同步控制问题,本文将平均偏差耦合策略与神经网络控制方法相结合,设计同步控制器实现双电机的同步运行。
1 预备知识
1.1 双电机伺服系统建模
图1为一种典型的机电位置伺服系统的结构示意图。
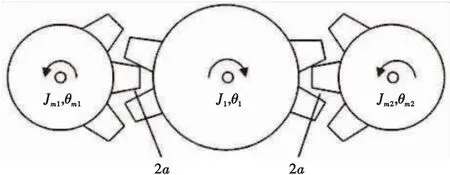
图1 双电机伺服系统示意图Fig.1 Schematic diagram of dual motor servo system
为了方便研究,假设传动比为1,齿隙为2a。据图1可得双电机驱动伺服系统动力学方程为
(1)
式中:Jmi和Jl是指电机惯性和负载惯性,bm和bl是电机粘性摩擦系数和负载粘性摩擦系数,θmi和θl代表电机角位置和负载角位置,ui是系统输入扭矩,Ti是电机和负载之间的传递力矩。zi为主、从动轮的相对角位移,定义zi=θi-θm,齿隙模型表示为
(2)
式中:k是扭矩系数,α是齿隙宽度。Ti可以被重新表示为
Ti=kzi+kdαi,
(3)
式中:kzi是线性部分,kdαi是非线性部分,定义dαi表示为:
(4)
定义系统的状态变量为

(5)

(6)
(7)
(8)
假设1:系统期望轨迹的1,2,3阶导数存在且有界。
假设2:非线性动力学f1,f2未知且有界。
由于存在未知非线性f1,f2,很难控制多电机驱动伺服系统。径向基神经网络用于近似系统非线性f1,f2如下所述:
(9)
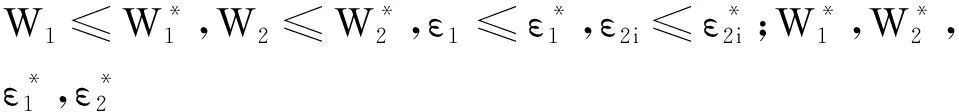
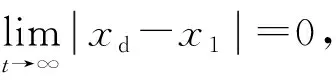
2 漏斗控制器算法实现
在本章中将设计一个基于非光滑漏斗误差曲面的漏斗控制器,主要目标是对系统(1)提出一种跟踪控制方案,使任意闭环信号具有全局一致有界性,同时输出跟踪误差始终保持在规定的漏斗性能函数上。另一方面,将平均偏差耦合策略与神经网络控制方法相结合,设计了同步控制器。
2.1 非光滑漏斗误差面概述
由于漏斗控制的高增益特性,跟踪误差可以被规定在漏斗区域内。
将漏斗的边界函数定义为
F(t):={z(t)∈R|φ(t)·|z(t)|<1},
(10)

(11)
因此, 当跟踪误差z(t)靠近边界时,要增加控制增益μ(t);相反,当跟踪误差z(t)超出边界,要相应减少控制增益μ(t)。图2给出了有界漏斗内的误差演化。
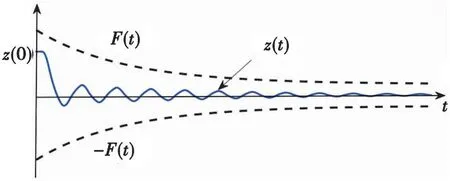
图2 漏斗中的误差演化Fig.2 Error evolution in funnel
设计漏斗边界函数如下:
F(t)=(φ0-φ∞)e-at+φ∞,
(12)
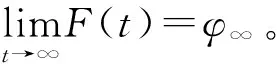
为了进一步提高跟踪性能,本文采用如下非光滑误差变换[12]来设计控制器:
(13)
其导数为
(14)
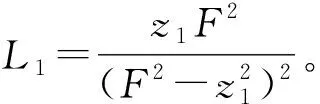
利用漏斗变量的高增益特性,每当z1(t)→F(t)时ν1→∞,这意味着我们可以通过漏斗变量式(13)来实现误差约束,此函数满足初始条件的限制,并且新的变量ν1不受系统次数的限制,因此改进的漏斗函数在实际中有着更广泛的应用。
2.2 跟踪控制器的设计
不同于标准反推法设计,本文采用动态面与反推法相结合的控制方法,可以消除反步时的微分爆炸问题。
本文采用如下坐标变换:
z1=x1-xd,
(15)
zn+1=xn+1-sn(n=1,2,3)。
(16)
引用如下一阶低通滤波器:
(17)
式中:αn为虚拟控制信号,sn为滤波器的输出,λn为滤波时间常数。
滤波误差定义为
efn=sn-αn。
(18)
选择实际虚拟控制律α1,α2,α3分别为
(19)
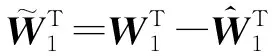
选择控制输入ui为
(20)
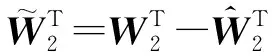
2.3 同步控制器的设计
对于多电机驱动系统,需要设计一个保证同步性能的同步控制器,定义两电机位置的平均位置误差、平均速度误差、误差函数为
(21)
同步控制器设计为
(22)
其自适应律为
(23)
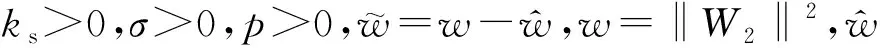
2.4 稳定性分析
定理1:由系统(6),控制器(20)组成的自适应神经网络闭环系统的误差变量z=(z1,z2,z3,z4)有界,且按指数收敛到原点的一个充分小的邻域内,只要神经网络的自适应律取
(24)
(25)
式中:ψ1,ψ2,Γ1,Γ2为正设计参数。
证明:取Lyapunov函数

(26)
对式(26)求导可得

(27)
根据杨氏不等式得
(28)
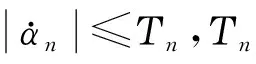
将式(28)和式(24)、式(25)代入式(27)可得

(29)
可以进一步写成
V≤-CV+π,
(30)
式中:
(31)
(32)
对式(30)两边求积分可得
(33)
因此,所有的系统状态都是有界的,双电机伺服系统的跟踪误差将收敛到原点的一个小邻域内。
根据式(26)和式(33)可得
(34)
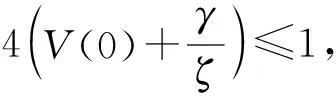
(35)
进一步说明:
(36)
由式(36)可以发现,在典型漏斗变量中引入非光滑函数,跟踪误差z1收敛在一个比预设的小得多的漏斗中。
定理2:考虑多驱动系统(5),当同步控制信号和自适应律选择为(22)和(23),同步误差是半全局最终一致有界的。
证明:取Lyapunov函数
(37)
对式(37)求导得
(38)
根据杨氏不等式得
(39)
将式(21),(22)和(39)代入式(38)可得
(40)
根据杨氏不等式得
(41)
将式(41)代入式(40)有
Vs≤-κVs+b,
(42)
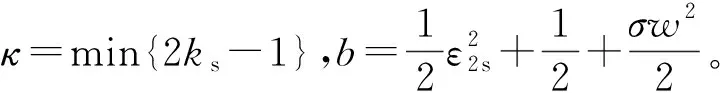
对式(42)两边求积分可得
(43)
根据李亚普诺夫稳定性理论,确定了同步误差是半全局最终一致有界的。
3 仿真结果及分析
在Matlab上进行仿真实验对所设计的控制算法进行验证,选择双电机驱动系统的参数为:Jm=0.185 kg·m2,bm=1.2 N·s/rad,Jl=0.028 kg·m2,bl=1.3 N·s/rad,k=56 N·m/rad,α=0.2 rad。
为了验证本文控制算法的有效性,将PI控制、动态面控制(dynamic surface control,DSC)与本文的非光滑漏斗控制(non-smooth funnel control,NSFC)控制方法进行仿真对比与分析。
1) 非光滑漏斗控制:漏斗边界函数设计如式(12),其参数为φ0=1,φ∞=0.1,a=0.9;跟踪控制器设计如式(19)和式(20),参数选择k1=50,k2=300,k3=350,k4=280;自适应率设计如式(24),(25),参数选择为ψ1=0.002,ψ2=0.035;同步控制器和其自适应律设计如式(40),(41), 参数选择为r=12,σ=0.01,ks=1。
2) PID控制器的参数:kp=150,ki=5,kd=0.1。
3) 动态面控制器的参数:k1=30,k2=400,k3=600,k4=650,λ1=0.001,λ2=0.001,λ3=0.000 1;
选择系统的初始状态为x1=0.2,x2=0,x31=0.3,x32=0.1,x41=0,x42=0。
选择期望信号为xd=0.5sin (t),负载跟踪效果和电机同步效果如图3—图7所示。
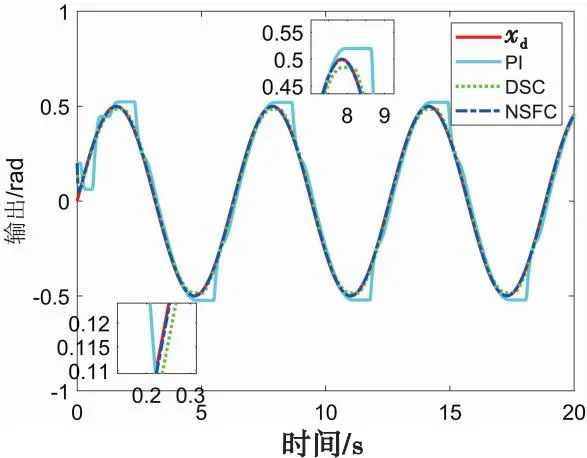
图3 三种方法的x1和xd的跟踪曲线Fig.3 Tracking curve of sum of three methods
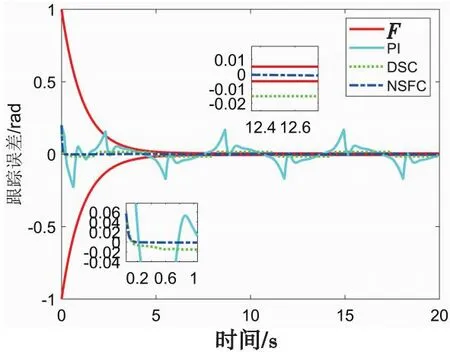
图4 跟踪误差曲线Fig.4 Tracking error curve
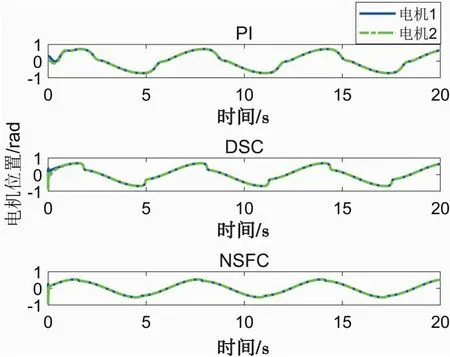
图5 双电机位置同步曲线Fig.5 Double motor position synchronization curve
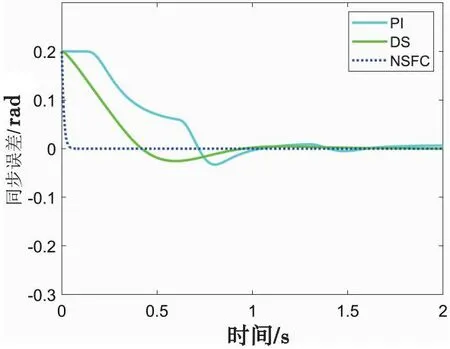
图6 同步误差曲线Fig.6 Synchronization error curve
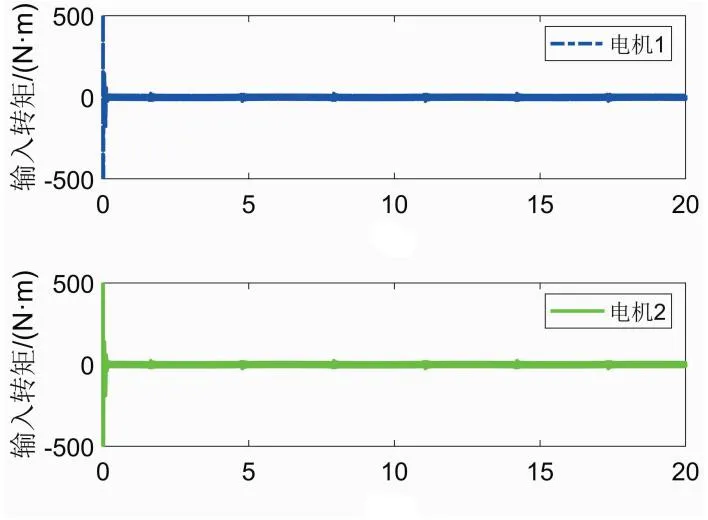
图7 控制输入曲线Fig.7 control input curve
从图3中可看出,相比于PI控制和动态面控制, 所提出的非光滑漏斗控制具有更好的跟踪性能;从图4中可以发现,非光滑漏斗控制的跟踪误差都被包含在漏斗边界函数内, 而PI控制和动态面控制的跟踪误差则超出了漏斗边界,这是因为没有采用漏斗函数进行误差转换;从图5中可看出,本文所提出的平均偏差耦合同步控制器具有更好的同步效果。
为了比较控制器的控制性能,基于3种控制策略性能指标详细对比如表1所示。

表1 仿真结果性能指标对比Tab.1 Comparison of simulation results and performance indicators
从表1中可以看出:
从表中数据可以看出,本文所提出控制器可以使得双电机伺服系统迅速高效地运行,达到较小的负载跟踪误差与电机同步误差。
为了进一步验证所提出的非光滑漏斗误差面具有更好的跟踪误差收敛,本文分别进行了漏斗控制(funnel control,FC) 和基于非光滑误差面的漏斗控制的仿真实验,其对比结果如图8和图9所示。
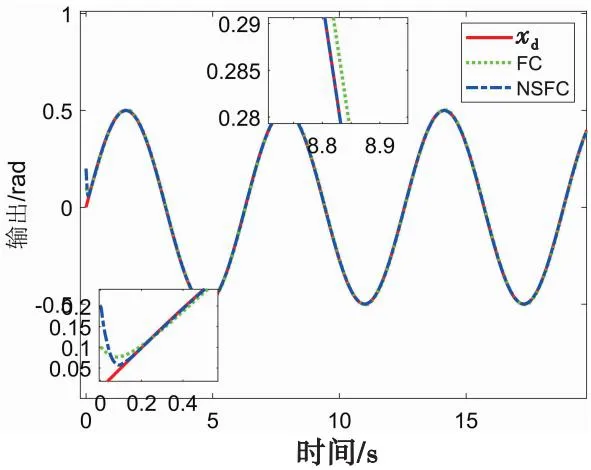
图8 负载位置跟踪曲线Fig.8 Load position tracking curve
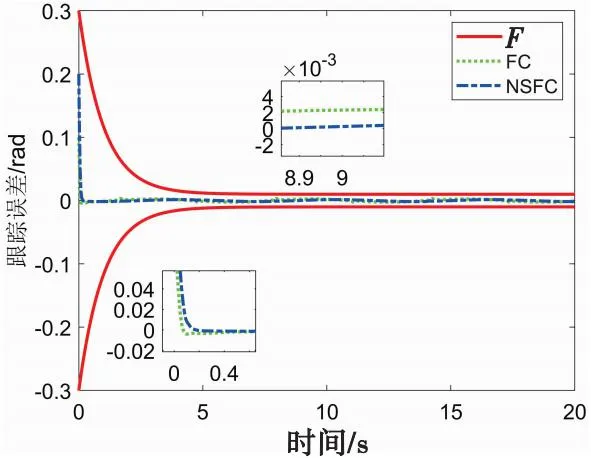
图9 跟踪误差曲线Fig.9 Tracking error curve
从图8和图9中可看出,与漏斗控制相比,非光滑漏斗控制在跟踪误差的暂态性能(超调量和调整时间)和稳态性能(稳态误差)方面都具有更好的控制性能。
4 结论
本文以具有未知非线性的双机电伺服系统为研究对象,设计了基于非光滑漏斗误差面的跟踪控制器,引入一阶滤波器对虚拟控制信号进行近似求导。该控制器能保证输出跟踪误差始终收敛于规定的漏斗边界函数内,同时设计的同步控制器实现了双电机的同步运行。采用Lyapunov方法证明了系统的跟踪误差和同步误差是一致最终有界的。仿真结果表明,本文所提出的控制方法能够提高系统的负载跟踪与电机同步性能。

