一组有趣的组合公式

☉山东建筑大学管理工程学院 田 心

设p是任意正整数，数列的通项公式ak=（-1）kkp，k=0，1，2，…，n.在求这个数列之和时，发现n和p有着密切的关系.当n＞p时比较好求，当n=p时感到困难，当n＜p时就更难求了.关键问题是如何处理kp的问题.为了解决这个问题，我们推导出三个公式.这三个公式的证明顺序是：先证明公式1，利用公式1证明公式2，最后利用公式1和公式2证明公式3.证明这三个公式都要用数学归纳法，在证明过程中都要用到二项式定理，由于证明方法类似，我们将公式1和公式2写出，只证明公式3.

一、三个组合公式

公式1：设p是任意正整数，当n＞p时

公式2：设p是任意正整数，当n=p时（-1）pp！.

公式3：设p是任意正整数（p-1）p！.

我们证明公式3.

证明：用数学归纳法证明.

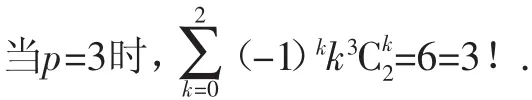
假设p=m-1，p=m时等式成立，再证当p=m+1时等式也成立.

事实上，由归纳假设，注意利用公式1和公式2及二项式定理得：

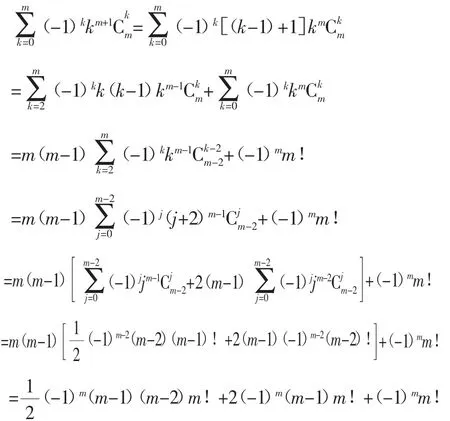
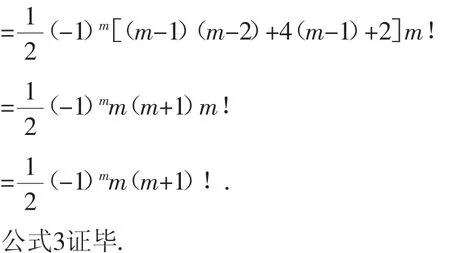
二、三个组合公式的推广及应用

显然，由公式2得到：

证明：由公式3和公式2得：

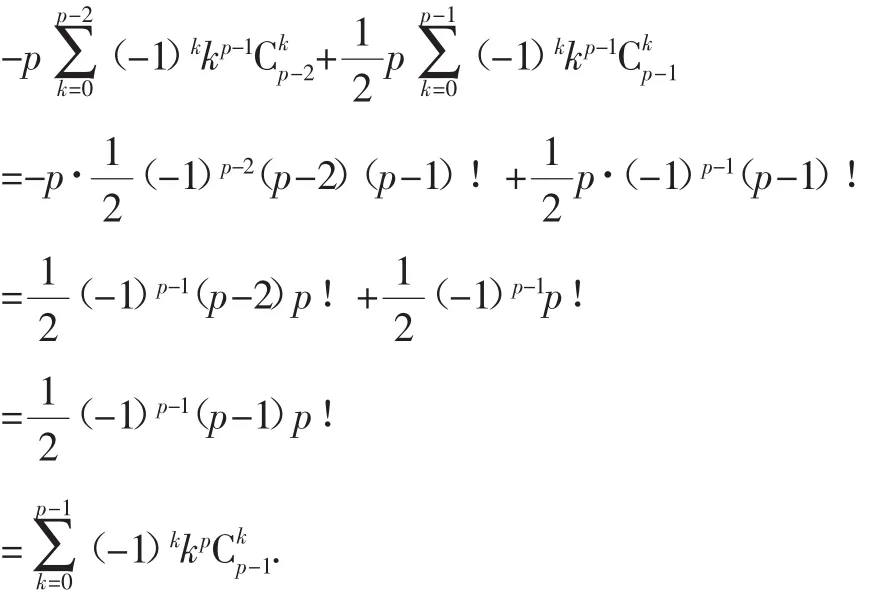
由公式1，利用二项式定理得：

公式6：对任意的正整数p和自然数m，当n＞p时，均

由公式1、公式2和二项式定理得：

公式7：对任意的正整数p和自然数m，均有（k+m）p=（-1）pp！.

公式6和公式7的证明方法和公式8的证明完全类似，我们就省略了.下面我们利用公式1、公式2、公式3和二项式定理证明公式8.

证明：由二项式定理和公式1、公式2、公式3得：

下面举三个例子来看一下这些公式的应用.

例1试求数列ak=（-1）（kk+1）100Ck10（1k=0，1，2，…，101） 的前102项之和与数列bk=（-1）k（k+16）100Ck102（k=0，1，2，…，102）的前103项之和.

解析：由公式6得：

例3试求数列ak=（-1）（kk+1）100（k=0，1，2，…，99） 的前100项之和与数列bk=（-1）k（k+16）100Ck99（k=0，1，2，…，99）的前100项之和.

解析：由公式8得：

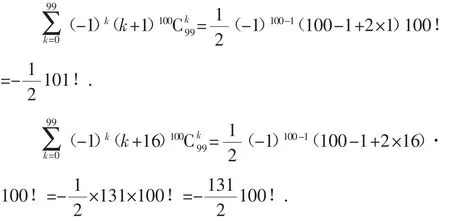
本文的工作还可以继续做下去.比如求，望有兴趣的读者努力.F