浅议知识的源头与上游的教学意义

☉青海省西宁市第二中学 赵小卫

源头之下有无限的可能，具有强大生命力的源头才能不停泛起思想的涟漪，推演出无尽的变化，更能有效激发出具有开拓性的创造力，事实上在知识与问题之间尤其不能只徘徊于知识的下游，或仅在知识的末端就耗尽我们的一切，正如墨子所言“原浊者，流不清”，为此关注数学知识及方法的上游和源头才能找到数学思想的根基，唤起人们最原始的求知欲和创造力.源头在于开创，知识的上游决定着知识体系的设计和应用方法的形成，倘若只局限于知识的下游最多也只能解决在相关知识体系下的个别问题，而难以找到全新的视角和开创性的举措.

从求知到求解如果没有“源文化和源思想”我们很多时候就只能无助的困在原地.从源头或者上游进行审视，必能清醒我们的头脑，引导推理的路径，合理我们的选择，提高求解时的效率.以下借助几个问题推本溯源，从相关知识的上游对这些问题做一个审视.

一、重温Ceva定理

为证三角形中的三线共点，人们可谓是用尽了办法，从不同的角度用不同的方法来予以诠释和证明，目前除了一些平面几何的方法，还有向量法以及用杠杆原理作为工具的物理方法等.抛开各种技巧如果按照从源头顺流而下的方式思考，这就需要先重温一下Ceva定理：

Ceva定理 设D、E、F分别为三角形ABC的边BC、CA、AB上的点，且=γ，则直线AD，BE，CF共点的充要条件是λμγ=1.

这是一个三角形中有关三线共点的定理，如果置Ceva定理在知识的上游，那么自Ceva定理顺流而下，向下审视我们就会看到三角形的内心、外心、重心、垂心、旁心，还有葛耳刚纳点等一些貌似互不相干的问题，推本溯源其实都是Ceva定理下的几个特殊情况，如图1.相反如果孤立起来看将永远看不到三角形这些特征的统一性.

图1

二、问题在课堂引发的冲突与思考

题1 如图2所示，二次函数y=ax2+bx+c（a≠0）的图像经过点（-1，2），且与x轴交点的横坐标分别为x1，x2，其中-2＜x1＜-1，0＜x2＜1，则函数关系式中a的取值范围是什么？

课堂实录：这一问题在学生的练习中出现了以下两种不同的算法和结果：

学生1：由图2可知，a+b+c＜0； ①

a-b+c=2； ②

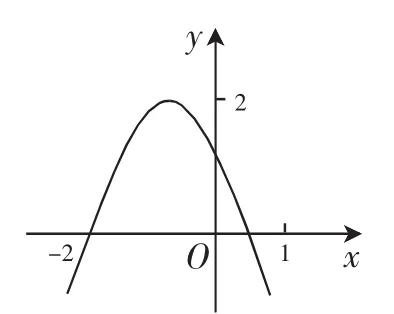
图2

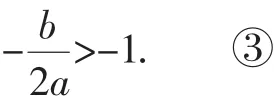
其中，从③得b＞2a，a＜.

由②得c=b-a+2. ④

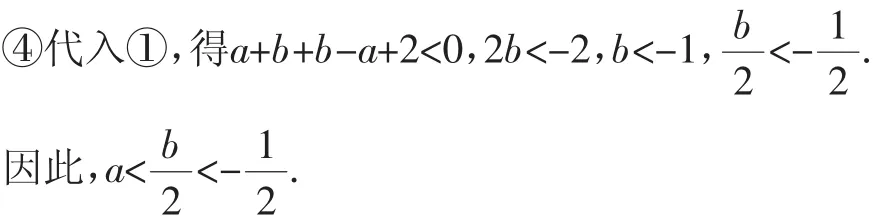
实录：当这一解法呈现出来的时候，几乎所有的人都认为这已经是确信无疑的了，一位平时很有主见而且数学成绩较优异的同学，在默默思考后又给出了如下的另外一种解法：

学生2：由题意知，a-b+c=2； ①

a+b+c＜0； ②

4a-2b+c＜0. ③

由①得b=a+c-2. ④

将④代入②，得a+a+c-2+c＜0，2a+2c＜2，a+c＜1， ⑤

将④代入③，得4a-2（a+c-2）+c＜0，4a-2a-2c+4+c＜0，2a-c＜-4. ⑥

⑤＋⑥，得3a＜-3.

因此a＜-1.

实录：这位同学无疑给平静的湖面投下了一枚不小的石子，顿时疑惑和不解自此开始回荡在学生中间……

回顾一下，两个结论相比很明显 {a∈R|a＜-1}⊂

，说明其中的一个要么冗余，要么漏解，

这让大家如何取舍呢？面对突如其来的情况，大家做出的第一反应是重新检查两位同学的解题过程，可并没有找到非常明显的破绽，那就只好利用特例来进行检验，在检验中大家慢慢开始对方法1逐渐产生了怀疑，细究起来方法2应该比方法1的精确度更好一些，方法1的偏差主要是由“二次放大”造成的.如果对于这一点课前毫无意识，恐怕一堂课会留下无以弥补的质疑和迷茫.

三、对二次函数取最值的多重理解

（1）二次函数y=a（x-x1）（x-x2）表示和x轴有两个交点并且交点坐标分别是（x1，0）和（x2，0）的这样一条抛物线，我们还可以将其变形成y=-a（x-x1）（x2-x），当x1＜x＜x2时，由基本不等式mn≤ （）2所讲“和定积最大”可得，

当x-x1=x2-x，即x=时，如果a＜0，则y取最大值；如果a＞0，则y取最小值.

（2）以上从几何角度来看，当x1＜x＜x2时，x-x1和x2-x可以作为一个矩形的两条边，按照“边数及周长给定的多边形，以正多边形面积最大”这一定理，当x-x1=x2-x，即x=时，矩形的长和宽两边相等，矩形成为正方形时，面积（x-x1）（x2-x）取最大值，此时，如果a＜0，则y取最大值；如果a＞0，则y取最小值.

当然，即便抛物线与x轴没有公共点，我们依然可以通过坐标系的平移变换，用同样的方法对二次函数y=ax2+bx+c（a≠0）取得最值的条件和最值的大小予以讨论.

（3）令f（x）=ax2+bx+c（a≠0），由f′（x）=0，得x=-判别导数两侧的符号，列表如下：

a的符号 -∞，-b 2a（ ）-b 2a -b 2a，+∞（ ）f′（x）-0+a＞0f（x）↘取极小值4ac-b2 4a↗f′（x）+0-a＜0f（x）↗取极大值4ac-b2 4a↘

以上站在源自不同方向知识的上游，从不同的角度对同一问题进行相互印证，这既可以体现出数学思想方法的科学性，又能反映出数学知识的内在关系，如果没有来自知识上游的文化审视，就不能形成从不同视角可以聚焦在一起的知识体系.

四、可叩问反函数以寻求答案的一个问题

我们知道函数y=（fx）的图像和它的反函数y=f-（1x）的图像关于直线y=x对称.而反比例函数y=的图像本身就关于直线y=x对称，这说明反比例函数y=其反函数上的点仍就在y=的图像上.并且相互对称两点的横纵坐标顺序相反.

题2（2015年成都卷）已知：一次函数y=-x+4的图像与反比例y=（k为常数，且k≠0）的图像交于A（1，a），B两点.

（1）求反比例函数的表达式及点B的坐标；

（2）略

分析：由题意，a=-1+4=3，所以A（1，3），k=1×3=3.

所以所求反比例函数解析式为y=.

又双曲线y=关于直线y=x对称，直线y=-x+4垂直于直线y=x，所以点A和点B关于直线y=x对称，从而由互为反函数的图像关系可知A、B两点的横纵坐标次序相反，因此所求B点坐标为（3，1）.

五、来自定比分点的观点

题3 如图3，在平面直角坐标系xOy中，抛物线y=ax2-2ax-3a（a＜0）与x轴交于A、B两点（点A在点B的左侧），经过点A的直线

l：y=kx+b与y轴负半轴交于点C，与抛物线的另一个交点为D，且CD=4AC.

（1）直接写出点A的坐标，并求直线l的函数表达式（其中k、b用含a的式子表示）；

（2）、（3）略.

图3

分析：设P1、P2是直线l上两点，点P是l上不同于P1、P2的任意一点，则存在一个实数λ，使=λ，λ叫做P分有向线段所成的比.进一步，如果有P（x，y）、111P2（x2，y2）、P（x，y），那么

根据题意，A（-1，0），C（0，b）按定比分点坐标关系式易得D点的横坐标x可满足=0（其中λ=4），解得x=4，从而D（4，5a）.然后再通过待定系数法得直线l的解析式为y=ax+a.经类比，过点D向x轴引一条垂线，再根据平行线分线段成比例定理就可以用平面几何的方法计算出D点的横坐标了.

六、小结

对于问题，它只是一个问题的终结，还是一系列问题的开始；对于方法，它能否是一个可以得到广泛应用的方法，还是一个完全被禁锢仅此而已的做法.我们对问题的把握是否存在曲解数学的情况，还是根本就没能抓住数学的灵魂，问题若不能产生出足够的思想和智慧就会失去真正的数学价值.

寻求文化自信就必须突出对思想与知识源头的思索，哪些内容和方法属于同根同源，有助于把分散的知识面收缩成知识点.看到不同内容的“血缘”关系，源头既是知识的根又是孕育思想的魂，正如唐朝的重臣魏征所言：臣闻求木之长者，必固其根本；欲流之远者，必浚其泉源；思国之安者，必积其德又.源不深而望流之远，根不固而求木之长，德不厚而思国之安，臣虽下愚，知其不可.F