近邻概率距离在旋转机械故障集分类中的应用方法
李霁蒲, 赵荣珍(兰州理工大学 机电工程学院,兰州 730050)
旋转机械故障诊断本质上是故障的模式辨识的过程。该项技术的当前发展中,随着数据获取和数据存储技术的长足发展,导致描述故障状态的特征维度不断增加,同时也增加了大量的冗余信息,这为后续的模式识别带来了极大的难度,为此,关于高维数据的降维成为了一项重要任务。对此,在计算机科学研究中,关于降维问题已取得一系列的研究进展,典型的如主成分分析方法(Principal Component Analysis, PCA)[1]、线性Fisher判别(Linear Fisher Discriminant,LFD)[2]、局部保持投影(Locality Preserving Projection,LPP)[3]、局部线性嵌入(Locally Linear Embedding,LLE)[4]、拉普拉斯特征映射(Laplacian Eigenmap, LE)[5]、等距映射法(Isometric Mapping,ISOMAP)[6]、随机近邻嵌入(Stochastic Neighbor Embedding,SNE)[7]等。其中,PCA是一种寻找最小均方意义下原始数据的最优低维表示的线性投影方法。LFD为通过数据间的类别信息,使数据间类内散度最小、类间散度最大。LPP为非线性方法拉普拉斯特征映射LE的线性近似,它既解决了PCA等传统线性方法难以保持数据非线性流行的缺点,还能够解决非线性难以获得新样本投影的缺点[8]。已在图像识别领域取得了一定的研究进展。
在机器学习中,度量学习(Metric Learning)已成为了非常重要的基础性命题。距离度量函数可评价不同样本之间的相似性,因此,距离函数显著地影响着大部分机器学习算法的性能。其中,欧式距离是众多机器学习中应用最为广泛的距离函数。欧式距离表示数据点间的直线距离,假定数据点的特征同等重要且互不相关。但是在一些实际情况下,如文献[9]中所述,欧式距离不能很好揭示样本之间的相似程度。SNE算法将高维数据间的欧式距离转化为概率表达形式,故受SNE算法的启发,本文提出近邻概率距离(Nearby Probability Distance)这一新的度量函数。
LPP作为局部保持的流形学习算法,局部邻域与权重的构建通常是基于欧式距离。K近邻(KNN)分类器作为一种简单、高精度的智能分类器,它在选择近邻点时也是基于欧式距离。但是,欧式距离有时并不能反映真实的数据空间结构,同类数据的距离甚至大过异类数据的距离。针对这一问题,本文把新提出的近邻概率距离应用到LPP与KNN分类器中,提出基于近邻概率距离的LPP(Nearby Probability Distance Locality Preserving Projection,NPDLPP)和基于近邻概率距离的KNN(Nearby Probability Distance K-Nearest Neighbor,NPDKNN)分类器,通过实验证明了它们的有效性,拟为典型多通道的转子试验台上的故障诊断发展提供一些参考依据。
1 局部保持投影算法
LPP算法的基本思想[10]是:在保持数据局部结构特征不变的条件下,对于高维空间数据集中相距较近的两个点,寻找一个投影矩阵,使得高维空间相距较近的两个点在低维空间上的投影坐标也较近。
设定高维数据集为n个d维向量X={x1,x2,…,xn},低维嵌入空间的敏感特征集为n个r维向量Y={y1,y2,…,yn},(r< LPP通常用两种方法构建相邻无向图[11]:①ε近邻方式:若两点间的距离小于常数ε时,将两点相连。② K近邻方式:若一点在另一点最近的k个点中,则两点相连。 由于常数ε的选择通常需要大量实验才能取得最佳效果,且当数据分布不均匀时ε近邻方式并不适用,故绝大多数的研究采用K近邻方式。本文也只与K近邻方式进行比较。 从上可知yi=ATxi,其中投影矩阵A可通过最小化式(1)所示的目标函数得到,即 (1) 式中:Sij为权值矩阵S的一个元素。 (2) 式中:σ为热核宽度,σ>0。 利用式(3)计算投影矩阵A arg min(ATXLXTA) (3) 定义Lagrange函数为 g(a,λ)=aTXLXTa+λ(1-aTXDXTa) (4) ATXDXTA=I (5) 从而LPP算法变为一个求解特征值问题,即 XLXTA=λXDXTA (6) 那么上式的前r个最小非零特征值对应的特征向量就构成投影矩阵A=[a1,a2,a3,…,ar]。 由数学知识可知,一个定义在向量空间X函数D:X×X→R0,若D对于任意xi,xj,xk均满足下列性质,那么D称为一个度量函数(metric): 1) (xi,xj)+D(xj,xk)>D(xi,xk) (三角不等式) 2)D(xi,xj)≥0 (非负性) 3)D(xi,xj)=D(xj,xi) (对称性) 4)D(xi,xj)=0⟺xi=xj(可区分性) 严格的说,如果一个度量函数满足前三个性质却不满足第四个,则称该度量函数为一个伪度量。 SNE算法的提出,为高维数据数据降维提供了新的思路,它与传统的数据降维方法不同,将高维数据间的欧式距离转化为概率表达形式,是一种基于数据间相似度的降维方法。在SNE中,数据xi选择xj作为近邻的概率为Pij (7) 式中:Pij为xi选取xj作为近邻的概率。参数λ为相应高斯函数的方差参数,它的确定与最终确定的近邻数量有关系。Pij=0且数据间的相似度概率和为1。考虑到以xi为中心点的高斯分布,若xj越靠近xi,则Pij越大。反之,则Pij极小。 在高维空间中,欧式距离并不能真实地度量数据间的分布情况,同类故障样本点间的欧式距离可能比非同类数据点间的欧式距离更大,导致近邻选择不准确。基于此,在引入近邻选择概率的基础上,本研究提出一种新的度量距离,即近邻概率距离(Nearby Probability Distance,NPD),定义如下 (8) 由节1可知,LPP算法采用K近邻方式构建相邻无向图。而K近邻方式在选择k个近邻点时采用的是欧式距离度量方式。但是欧式距离有时并不能反映真实的数据分布状态,因此把近邻概率距离引入LPP当中。基于新的距离度量,寻找近邻点。NPDLPP算法具体步骤如下: 步骤1采用式(8)为距离度量构建相邻无向图,确定k个近邻。 步骤2构建权值矩阵。在相邻无向图中,作为近邻的点与点用边相连,权值的大小用来表示两点的相近程度。如果能够在定义权值时也考虑两点作为近邻的概率问题,将会使相近的两点权值更大,因此重新定义权值矩阵为 (9) 式中:α为用户设定的参数。 步骤3计算投影矩阵。根据式(9)代替Sij求解式(3),得到的r个最小非零特征值对应的特征向量就构成投影矩阵A=[a1,a2,a3,…,ar]。 传统KNN分类器其分类原理是:通过计算测试样本与各个训练样本之间的欧式距离,然后根据距离测量选择距离最近的k个样本,即为测试样本的k个近邻点。在k个近邻点中,哪一种类型拥有的点多,测试样本就属于这一类型。由此可见,传统KNN分类器赋予近邻样本特征相同的贡献,距离度量函数很大程度上影响着分类的效果。 随着维数的升高,点与点之间的欧式距离将变得越来越不明显,点到最近邻点及其最远邻点的距离几乎是相等的,非同类点的欧式距离可能比同类点的欧式距离更为接近,这将导致在选择近邻点时存在误差。近邻概率距离在选择近邻时,如果两点成为近邻的概率越大,则两点的距离将会被描述的更为贴近;反之,则两点的距离将会被描述的更远。这更利于近邻点的选择,因此将近邻概率距离引入KNN分类器中,提出基于近邻概率距离的KNN分类器(Nearby Probability Distance K-Nearest Neighbor,NPDKNN)。 NPDKNN分类器的基本思想是:计算未知类别测试样本与已知类别训练样本之间的概率距离,然后根据概率距离的大小选择k个近邻样本点,k个近邻样本点中数量最多的类别即为测试样本类别。设样本数为c,分别为L1,L2,L3,…,Ls类,s是类别数,k1,k2,k3,…,ks分别是k个近邻中属于L1,L2,L3,…,Ls类的样本个数。寻找k个近邻点使用的距离度量为式(8),定义判别函数为 gj(xi)=max{ki|i=1,2,3,…,s} (10) 决定规则为,如果gj(xi)=ki,则决策x属于Lj类(1≤j≤s)。 本文方法在一个典型转子实验台上实施的故障诊断的流程,如图1所示。该方法主要分为以下几个步骤。 图1 NPDLPP与NPDKNN相结合的故障分类方法流程图Fig.1 The flow char of the fault classification method of NPDLPP combined with NPDKNN 步骤1对采集信号使用文献[12]中的中值滤波与小波消噪算法集成的混合滤波方法进行消噪处理,对消噪后的振动信号集进行时域、频域的特征提取,得到原始高维数据特征集P。 步骤2将原始数据集P利用提出的NPDLPP进行降维得到低维敏感特征集Y。 步骤3将得到的低维敏感特征集Y输入到基NPDKNN分类器进行辨识,得到测试样本的故障类型。 输入:数据集X={x1,x2,…,xn},邻域数值k,热核参数σ; 输出:投影矩阵A。 本研究工作的实验对象为参考文献[13]图2所示的双跨度转子试验台。设备安装共有13个电涡流传感器。其中,12个传感器布置在6个截面处的相互垂直方位,采集不同方位的振动信号,第13个传感器布置在电机端,用于采集转速信号。在该设备上进行升降速实验,分别模拟转子不对中、质量不平衡、轴承松动、动静碰磨及正常转动5种状态实验。设置采样频率为5 000 Hz,转速为3 200 r/min,采集各种状态类型数据样本80组,其中50组作为训练样本,30 组作为测试样本。针对样本集每一个通道(共12个通道)构造时域频域特征集,共16×12=192个特征。确定的特征参数,如表1所示。各个参数的计算公式参考文献[14]。 表1 确定的特征参数情况Tab.1 Determine the characteristic parameters 本文需要设定的参数有:维数约简的目标维数d、NPDLPP中近邻参数k1、NPDLPP中权值矩阵参数α及NPDKNN中近邻参数k2。 其中,维数约简的目标维数d用极大似然估计方法计算为5维。不同的k1与α组合得到的降维效果在NPDKNN(固定参数k2=8)的识别率不同,设置k1的范围为6~20,间隔为1,α的范围为0.1~1,间隔为0.1,对所有的k1和α进行计算,结果如图2所示。 图2 整体识别率随k1与α的变化Fig.2 The overall recognition rate change with k1 and α 从图2可知,当k1=8时,整体识别率明显具有优势,当k1=8,α=0.5时,整体识别率达到最大值96%。采用固定单一分量α=0.5和k1=8的方法,见图3进一步说明最大值参数选择情况。 (a)当α=0.5时整体识别率随k1变化曲线 (b)当k1=8时整体识别率变化曲线图3 k1,α参数选择曲线图Fig.3 k1,α parameter selection curve 当确定k1和α的取值后,把降维后的低维敏感特征集输入到NPDKNN中,并设置k2的范围为6~20,其整体识别率随k2变化如图4所示。 图4 整体识别率随k2变化曲线图Fig.4 The overall recognition rate change with k2 通过上述分析可以看出,当参数k1=8,α=0.5,k2=8时,NPDLPP与NPDKNN整体识别率能达较为理想的效果,因此本文在试验分析中采用这些取值。 为更好的说明NPDLPP降维后数据的分布情况,本文采用文献[15]中的评价指标Je来定量描述降维后的类间散度及类内散度。Je越大,则说明类内离散度越小,类间离散度越大,降维效果越好。Je计算公式如下 (11) (12) (13) 为了使实验更具有说服力,本文分别利用PCA、ISOMAP、LLE、LPP等方法进行降维,并对比各个算法的降维效果。前三个主元的低维嵌入效果如图5所示(其中,“+”、“○”、“*”“◆”“□”分别代表转子不对中、质量不平衡、轴承松动、动静碰磨及正常各个状态),表2从数据角度反映各算法的降维效果。 从图5、表2中可知:图5(a)的降维效果最差,这是由于全局保持的线性降维方法并不能很好的显示低维流形特征。图5(b)作为非线性全局保持降维方法比5(a)降维效果好。图5(c)、图5(d)、图5(e)作为局部保持的降维算法能较好的反映低维嵌入流形特征。其中图5(e)的降维效果最好,明显使类内聚集在一起,类间分离开来。用评价指标Je评价图5中各个算法的降维效果,如表3所示。 从表3可知,PCA降维后的效果最差,类间距离并没有很好的分开,类内之间也没有很好的聚集。NPDLPP相对于其他算法具有明显的优势,评价指标Je达到了9.048 6,远远大于其他算法,因此NPDLPP具有一定优势。 为了证明本文提出的NPDKNN分类器的稳定性,本文选用了KNN分类器做比较。两类分类器分别在原始高维数据集添加随机噪声a=0.0、0.2、0.4、0.6的情况下(本文采用文献[16]中所述的方法),把经过NPDLPP降维后的低维敏感特征集输入到KNN与NPDKNN中,如表4所示。 (a) PCA (b) ISOMAP (c) LLE (d) LPP (e) NPDLPP图5 测试样本基于不同算法的降维效果Fig.5 Test sample based on different dimension reduction method results 表2 降维算法及其NPDKNN辨识准确率Tab.2 Classification identification method andthe NPDKNN recognition accuracy 表3 各个算法降维后的类间类内评价指标Tab.3 Each dimension reduction algorithm using theevaluation index in between the classes 从表4可知:①NPDKNN分类器的识别率大于KNN分类器,这是由于两个选择近邻点的方式不同,NPDKNN分类器选择近邻点的方式能更准确度量近邻点;②随着噪声干扰系数的增加,KNN分类与NPDKNN分类器识别率下降较多,但是NPDKNN分类器的识别率比KNN分类器普遍要高些,因此可以看出NPDKNN分类器拥有较为理想的抗干扰能力。 表4 KNN与NPDKNN受不同干扰程度噪声的影响Tab.4 The influence of KNN and NPDKNN under theinterference noise of different degree 针对高维空间特征集中各个故障类型的特征值存在一定“混淆”,从而导致故障类型难以辨别的问题展开研究,提出一种考虑了两点之间成为近邻的概率距离,即近邻概率距离(NPD),并把它应用于局部保持投影算法(LPP)和K-近邻(KNN)分类器中。在多域、多通道的典型转子试验台进行实验:首先将振动信号转化为多域、多通道的高维特征集;然后利用NPDLPP对高维特征集进行降维,得到低维敏感特征集;最后将低维敏感特征集输入到NPDKNN分类器中进行辨别。实验证明:NPDLPP对比LPP使类内距离更加靠近,聚类效果有了极大的提升,同时类间距离也进一步拉开,更有利于故障类型的判别;NPDKNN分类器能更精确、稳定的实现类型判别。因此,本文提出的NPDLPP与NPDKNN故障诊断方法具有较好的分类效果和较高的故障识别率,为转子故障诊断提供了一种新的解决思路。 参 考 文 献 [1] TURK M,PENTLAND A. Eigenfaces for recognition[J]. Journal of Cognitive Neuroscience,1991,3(1):71-86. [2] BELHUMEUR P N,HESPANHA J P,KRIEGMAN D J. Eigenfaces vs. Fisherfaces: recognition using class specific linear projection[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence,1997,19(7):711-720. [3] HE X,PARTHA N.Locality preserving projections[C]//Proceedings of the 17thAnnual Conference on Neural Information Processing Systems.Vancouver,2003:153-160. [4] SAM T R,LAWRENCE K S. Nonlinear dimensionality reduction by locally linear embedding[J].Science,2000,290(5500):2323-2326. [5] BELKIN M,NIYOGI P. Laplacian eigenmaps for dimensionality reduction and data representation[J].Neural Computation, 2003,15(6):1373-1396. [6] TENENBAUM J B,SILVA V, LANGFORD J C.A global geometric framework for nonlinear dimensionality reduction[J].Science,2000,290(5500):2319-2323. [7] HINTON G,ROWEIS S.Stochastic neighbor embedding[J].Advances in Neural Information Processing Systems,2003,15(3):833-840. [8] 王雪冬,赵荣珍,邓林锋.基于KSLPP与RWKNN的旋转机械故障诊断[J].振动与冲击,2016,35(8):219-223. WANG Xuedong,ZHAO Rongzhen,DENG Linfeng.Rotating machinery fault diagnosis based on KSLPP and RWKNN[J].Journal of Vibration and Shock,2016,35(8):219-223. [9] 王微.融合全局和局部信息的度量学习方法研究[D].北京:中国科学技术大学,2014. [10] 杨望灿,张培林,张云强.基于邻域自适应局部保持投影的轴承故障诊断模型[J].振动与冲击,2014,33(1):39-44. YANG Wangcan,ZHANG Peilin,ZHANG Yunqiang.Bearing fault diagnosis model based on neighborhood adaptive locality preserving projections[J].Journal of Vibration and Shock, 2014,33(1):39-44. [11] 杨庆,陈桂明,何庆飞, 等.局部切空间排列算法用于轴承早期故障诊断[J].诊断、测试与诊断,2012,32(5):831-835. YANG Qing,CHEN Guiming,HE Qingfei,et al.Vibration suppression of pipe system with tuned mass damper[J].Journal of Vibration, Measurement & Diagnosis,2012,32(5):831-835. [12] 赵荣珍,李超,张优云.中值与小波消噪集成的转子振动信号滤波方法研究[J].振动与冲击,2005,24(4):74-77. ZHAO Rongzhen,LI Chao,ZHANG Youyun.Filter design synthesizing median filtering and wavelet algorithm to de-nose vibration signal polluted by violent pulse noises[J].Journal of Vibration and Shock, 2005,24(4):74-77. [13] 王雪冬,赵荣珍,邓林锋.基于PCA-KLFDA的小样本故障数据集降维方法[J].华中科技大学学报(自然科学版),2015,43(12):12-16. WANG Xuedong,ZHAO Rongzhen,DENG Linfeng.Small sample size fault feature data recognition based on the PCA-KLFDA[J].Journal of Huazhong University of Science and Technology(Natural Science Edition),2015,43(12):12-16. [14] 马婧华.基于流形学习的旋转机械早期故障融合诊断方法研究[D].重庆:重庆大学,2015. [15] 吴剑.基于特征选择的无监督入侵检测方法[J].计算机工程与应用,2011,47(26):79-82. WU Jian.Unsupervised intrusion detection based on feature selection[J]. Computer Engineerng and Applications, 2011,47(26):79-82. [16] CHEN F, TANG B, CHEN R. A novel fault diagnosis model for gearbox based on wavelet support vector machine with immune genetic algorithm[J]. Measurement, 2013, 46(1): 220-232.
2 提出一种新型的度量函数近邻概率距离

3 近邻概率距离在故障诊断上的应用
3.1 基于近邻概率距离的局部保持投影算法
3.2 基于近邻概率距离的KNN分类器
4 故障诊断上的应用方法设计

5 实验结果与讨论
5.1 实验数据

5.2 参数设定




5.3 评估方法

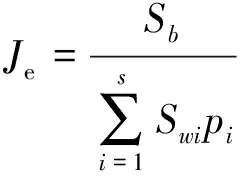

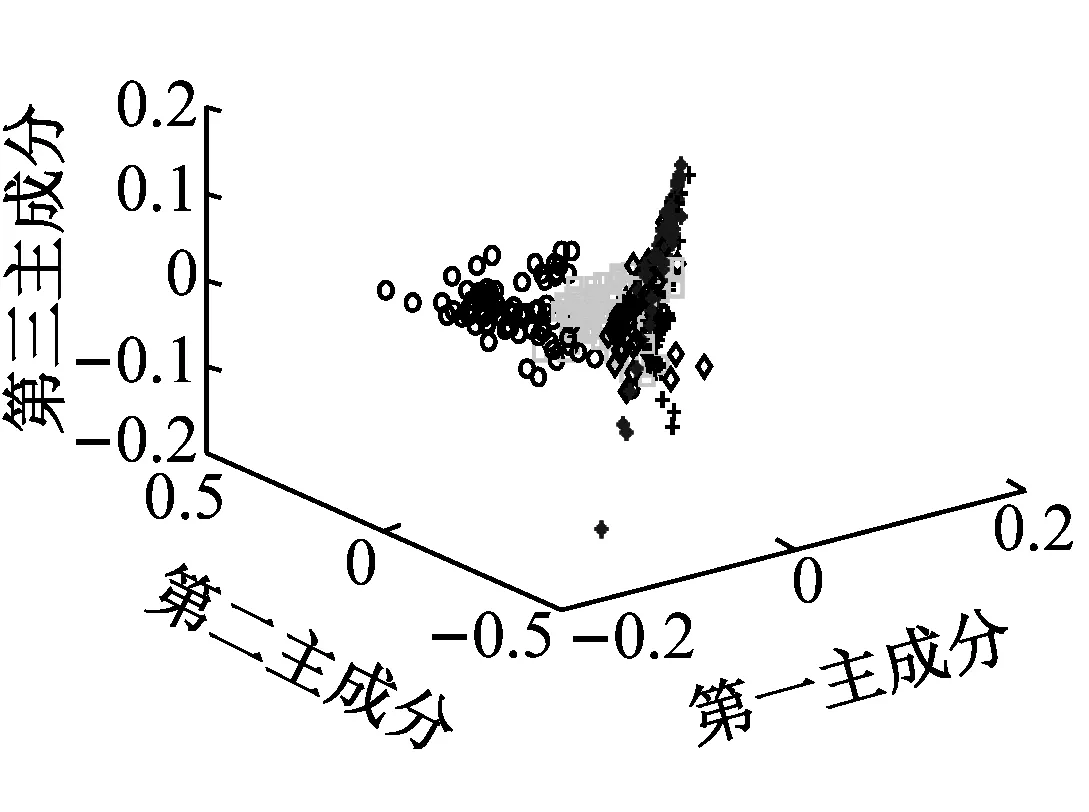
5.4 实验分析







6 结 论

