上覆非饱和层的饱和地基稳态响应分析
胡安峰, 李怡君, 贾玉帅(1.浙江大学 浙江大学滨海和城市岩土工程研究中心,杭州 10058;2.浙江大学 软弱土与环境土工教育部重点实验室,杭州 10058;.广州市建筑质量安全监测中心,广州 510600)
地基在动荷载作用下的振动问题是一直是工程领域关注的重点。在20世纪初,Lamb[1]就对弹性半空间表面作用点源及线源脉冲荷载所产生的扰动问题进行了研究。而实际地基土体并非理想弹性介质,而是一种复杂的多相介质。1956年,Biot[2-3]研究了饱和多孔介质的波动传播机理,并提出了考虑固液耦合的饱和多孔弹性介质波动方程。迄今为止,大多数学者还是基于该理论对饱和土的动力问题进行研究。Paul[4]采用Laplace-Hankel变换得到了饱和弹性半空间的Lame问题解。Philippacopoulos[5]通过引入势函数将波动方程解耦,研究了饱和半空间在表面荷载作用下波动的传播与消散问题。王立忠等[6]在略去流体相对于土骨架的惯性力,并假定水是不可压缩的基础上,给出了饱和弹性半空间在低频谐和集中力下的积分形式解。陈龙珠等[7]通过积分变换技术求得了线源和点源两种情况下的Lame问题积分形式解。
在上述文献中,研究者多把地基土体当做均匀介质,而天然地基土体在地下水位上下的性质存在较大差异,基于此,一些学者采用弹性层和饱和半空间分层模型[8-10]来研究其动力响应,即将地下水位以下土体近似地视为饱和半空间,地下水位以上的土体考虑为理想弹性层。不可否认,此模型具有较强的工程背景,但实际上地下水位以上的土体并非理想弹性介质,而是具有一定含水率的三相非饱和介质,故将地基简化为上覆非饱和层的饱和半空间模型更接近实际[11]。目前,关于非饱和介质动力理论的研究才刚刚起步。Brutsaert[12]利用等效流体模型将饱和土的Biot波动方程扩展到非饱和土。徐长节等[13]基于Vardoulakis等[14]提出的非饱和土的动力控制方程,对非饱和土中波的传播特性进行了分析。徐明江[15]在已有研究的基础上,重新推导了非饱和土的实用波动方程,并研究了非饱和半空间在任意分布的表面谐振荷载作用下的动力响应问题。
本文基于饱和土及非饱和土的动力控制方程,通过引入位移函数并利用双重Fourier变换,结合边界条件及连续条件给出了竖向简谐荷载作用下上覆非饱和层的饱和地基位移和应力积分形式解。通过将本文退化解与已有文献的结果进行对比,验证了本文解答的可靠性。最后结合数值算例,分析了上覆非饱和土层的饱和度、厚度以及地表透气透水条件等因素对地表竖向位移幅值与孔压变化的影响。
1 饱和土体动力控制方程求解
根据Biot饱和弹性多孔介质理论,在忽略惯性耦合项[16]的条件下,考虑稳态振动,则直角坐标系下饱和土的动力控制方程可表示为
(1a)
(1b)
(1c)

(2a)

(2b)

(2c)

(3)
式中:ui、wi分别为土骨架位移和孔隙水相对于土骨架产生的位移;p为孔隙水压力;i=x,y,z;(·)、(··)分别表示对时间t的一阶、二阶导数;λs=α2M+λ,λ和μs为饱和土骨架的Lame常数,α和M为考虑两相材料压缩性的Biot常数;ρ=nρf+(1-n)ρs,n为土的孔隙率,ρs和ρf分别为土骨架和孔隙水的质量密度;参数m=ρf/n;b为一个表示土渗透性的参数,b=ηd/k,其中ηd为流体动力黏滞系数,k为渗透系数。

(4)
式中:Φ,Ψ为任意函数,式(1)、式(2)和式(3)经整理后可得
(5a)

(5b)
(5c)

(5d)

根据Cauchy-Reimann条件,由式(5a)﹑ (5b)可得

(6a)

(6b)
定义算子
(7a)

(7b)

(7c)
(7d)
将上面定义的算子代入式(5c)﹑式(5d)和式(6a)、式(6b)得
(8a)

(8b)

(8c)

(8d)
由式(8b)和式(8c)可得

(9)
引入位移函数F(x,y,z),并令
(10a)

(10b)

(10c)
则式(8b)﹑式(8c)自动满足,将式(10)代入式(8a)得

(11)
定义双重Fourier变换及相应的逆变换为

(12a)
(12b)
对式(7)和式(11)进行双重Fourier变换,两式经整理后可得
(13)
式中:c1=μs(λs+2μs);
c2=[a6+(a5+a7)(λs+2μs)+(λs+μs)2(ξ2+η2)+a1a4μs];
c3=[a6(a5+a7)+a5a7(λs+2μs)-
a1a4(λs+2μs)(ξ2+η2)+a7(λs+μs)2(ξ2+η2)+
2a1a4(λs+μs)(ξ2+η2)+a1a4a5];
c4=a5a6a7-a1a4a6(ξ2+η2);a5=-(λs+2μs)(ξ2+η2)+a2;
a6=-μs(ξ2+η2)+a2;a7=-(ξ2+η2)-a3
与式(13)相应的特征方程是
c1λ6+c2λ4+c3λ2+c4=0
(14)
解上述特征方程可得到6个特征根:±λ1,±λ2,±λ3(Re[λj]≥0,j=1,2,3),故式(13)的解可表示为
(15)
对式(8d)进行双重Fourier变换可得
(16)

求解式(16)可得
(17)
对式(10)进行双重Fourier变换并将式(15)代入,整理后可得
(18a)

(18b)

(18c)
式中:
结合式(16)﹑式(18a)可得

(19a)

(19b)
由饱和土的本构方程可得

(20a)
(20b)

(20c)
对式(20)进行双重Fourier变换后, 将式(18)﹑式(19)代入可得
(21a)

(21b)

(21c)
式中:
b1j=-λs(ξ2+η2)Φj+(λs+2μs)λjUj-αPj,
b24=-iμsξλ0,b2j=-iμsη(λjΦj+Uj),
b34=iλ0μsη,b3j=-iξμs(λjΦj+Uj)
式(18b)﹑式(18c)、式(19a)、式(19b)及式(21a)~(21c)即为直角坐标系下饱和土半空间稳态动力响应在变换域内的一般解,式中Cj、Dj(j=1~4)为待定系数。
2 非饱和土动力控制方程求解
基于连续介质力学理论的守恒定律及Bishop等[17]非饱和土有效应力公式,通过联立非饱和土本构关系,运动方程,及连续性方程,可得到非饱和土动力控制方程表达式


(22a)

(22b)

(22c)

(22d)

(22e)

A24=-A25=-Sr(1-Sr),

采用与求解饱和土的动力响应类似的方法,得到直角坐标系下非饱和土半空间稳态动力响应在变换域内的一般解为

(23a)

(23b)

(23c)

(23d)

(23e)

(23f)

(23g)

(23h)
式(23a)~式(23h)中Aj,Bj(j=1~5)为待定系数,其余各参数的表达式见附录A。
3 边界条件及连续条件
设上覆非饱和土层的厚度为h,竖向简谐荷载F0作用在地表区域Ω内,如图1所示。荷载幅值为1 kN,频率ω=1 Hz。假定上覆非饱和层与饱和半空间孔隙率相同,且交界面处不透气不透水,则地表的边界条件及交界面处的连续条件可表示为

图1 上覆非饱和层饱和半空间计算模型简图Fig.1 Model of the saturated half-space with an unsaturated superstratum
(24a)

(24b)

(24c)

(24d)

(24e)

(24f)

(24g)

(24h)

(24i)
pl(x,y,h)+pg(x,y,h)-p(x,y,h)=0
(25a)
(25b)
(25c)
对于透气透水非饱和土层顶面,有
pl(x,y,0)=0
(26a)
pg(x,y,0)=0
(26b)
对于不透气不透水非饱和土层顶面,有
(26c)

(26d)
由于波的辐射特性,饱和半空间动力响应解中的正指数项将被舍弃,即C1=C2=C3=C4=0。根据以上分析,边界和连续条件个数等于未知数的个数,故可以求出未知系数Ai、Bi和Dj(i=1~5,j=1~4)。
对式(24)~式(26)中的边界条件及连续条件进行Fourier变换,将变换域内各动力响应分量的表达式代入,得到如下的方程
Kν=f
(27)
式中:
ν=(A1A2A3A4A5B1B2B3
B4B5D1D2D3D4)Τ
式中:Bij(i=1,2,3;j=1,2,3)的表达式见附录B。

由式(27)可得:ν=[K]-1f
(28)
式中:[K]-1为矩阵K的逆矩阵。
当向量ν确定后,将待定系数Ai、Bi和Dj代入各响应分量表达式,即可得到变换域内的稳态响应的积分形式解答。
4 算例分析
采用快速傅里叶变换(FFT)法对变换域内的位移﹑应力和孔压响应表达式进行数值Fourier逆变换。根据Cai等[18]的建议,选取和-16 m-1≤η≤16 m-1为积分区间,积分点为2 048×2 048,可满足精确性要求。
4.1 数值计算结果验证
当Sr=1时,非饱和介质的动力控制方程可以退化为饱和多孔介质的动力控制方程,分层地基退化为均质饱和地基。陈龙珠通过Fourier变换与Hankel变换得到了饱和地基Lame问题的积分形式解。图2给出了本文的退化解与陈龙珠解的对比。其中饱和土的物理参数取值为
λs=1.29×107N/m2,μs=1.94×107N/m2,n=0.6,ρf=1 000 kg/m3,ρs=2 700 kg/m3,M=2.1×109N/m2,α=1。
从图2可知,本文结果与陈龙珠的解吻合得较好,验证了本文求解方法的可靠性。

图2 本文解与陈龙珠解的对比Fig.2 Comparison with the results of Chen Longzhu


图3 本文解与杨峻解的对比Fig.3 Comparison with the results of Yang Jun
4.2 数值计算算例分析
非饱和土是一种由土骨架、孔隙水和孔隙气体三种介质组成的混合物,其中土骨架的物理参数取值如下:λu=1.29×107N/m2,μu=1.94×107N/m2,ρu=2 700 kg/m3,Ku=3.6×1010N/m2,n=0.6。两种孔隙介质的参数取值,如表1所示。为了研究方便,假设其它物理参数取值不受饱和度变化的影响。

表1 非饱和土孔隙介质参数Tab.1 Parameters of pore water and gas
图4给出了地表竖向位移响应在水平方向的分布图。从图4可知,上覆非饱和层饱和度越大,地表竖向位移幅值越大。同时,随着距荷载作用点距离的增加,荷载引起的振动波会发生衰减,距离越远衰减越大。此外,对比图4(a)和图4(b)可以发现,相同饱和度下地表透气透水时的竖向位移要比不透气不透水时的位移大。这是因为地表处于透气透水条件时,靠近地表附近的非饱和土层的孔隙水压力更容易消散,造成作用在土骨架上的有效应力增加,最终导致地表的竖向位移也相应变大。

(a)地表透气、透水

(b)地表不透气、不透水图4 非饱和土饱和度对竖向位移的影响Fig.4 Influence of the saturation on the vertical displacement
在实际工程中,由于受降雨、干旱等多种因素的影响,地下水位的高度会发生变化,相应地,上覆非饱和土层的厚度会随之变化。图5给出了地表透气透水条件下地表位移响应随非饱和层厚度变化的曲线图。从图5可知,随着非饱和层厚度的不断增大,地表竖向位移快速地减小,且饱和度越大,位移响应受厚度变化的影响越明显;当非饱和层厚度达到一定数值时,地表的竖向位移响应趋于稳定。因此,非饱和层厚度在一定的变化范围内对地表竖向位移影响明显,而这一范围与非饱和土饱和度以及荷载的大小等多种因素有关。

图5 上覆非饱和层厚度对地表竖向位移的影响Fig.5 Influence of the thickness of unsaturated soils on vertical displacement
图6为非饱和土层的孔隙水压力沿深度的分布图。对比图6(a)和图6(b)可以发现,当地表透气透水时,沿深度方向孔隙水压力由零快速增加到峰值然后逐渐减小,此时孔隙水压力的峰值发生在离地表较近的位置;当地表不透气不透水时,沿深度方向孔隙水压力由峰值逐渐得减小,此时孔隙水压力在地表达到最大。此外,从两图中还可以看出相同饱和度下地表透气透水时的孔隙水压力峰值小于不透气不透水时的孔隙水压力峰值。
5 结 论
本文采用解析的方法研究了上覆非饱和层的饱和半空间在谐振荷载作用下的稳态响应问题。通过引入位移函数并利用积分变换法,得到了上覆非饱和土的饱和半空间的动力响应问题的一般解。最后通过数值算例分析,得到以下结论:
(1)上覆非饱和土层的饱和度对分层地基的动力响应有显著的影响,饱和度越大,地表位移幅值也越大;此外,相同饱和度下地表透气透水时的竖向位移要比不透气不透水时的位移大。

(a)地表透气、透水

(b)地表不透气、不透水图6 地表透气透水情况对非饱和层孔隙流体压力的影响
Fig.6 Influence of the drainage-exhaust situation of foundation surface to the pore water pressure in unsaturated soils
(2)地下水位变化会引起上覆非饱和层厚度的变化,当非饱和层厚度较小时,随着厚度的不断增大,地表竖向位移快速地减小;当非饱和层厚度达到一定数值时,随着厚度的增大地表竖向位移变化趋于稳定。
(3)当地表透气透水时,孔压响应沿深度方向由零快速增加到峰值然后逐渐减小;当地表不透气不透水时,沿深度方向孔压由峰值逐渐减小。相同饱和度下地表透气透水时的孔隙水压力峰值小于不透气不透水时的孔隙水压力峰值。
参 考 文 献
[1] LAMB H. On the propagation of tremors over the surface of an elastic solid[J]. Philosophical Transactions of the Royal Society of London, 1904, 203:1-42.
[2] BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. higher frequency range[J]. Journal of the Acoustical Society of America, 2005, 28(2):179-191.
[3] BIOT M A. Mechanics of deformation and acoustic propagation in porous media[J]. Journal of Applied Physics, 1962, 33(4): 1482-1498.
[4] PAUL S. On the disturbance produced in a semi-infinite poroelastic medium by a surface load[J]. Pure & Applied Geophysics, 1976, 114(4):615-627.
[5] PHILIPPACOPOULOS A J. Lamb’s problem for fluid-saturated, porous media[J]. Bulletin of the Seismological Society of America, 1988, 78(2):908-923.
[6] 王立忠, 陈云敏, 吴世明,等. 饱和弹性半空间在低频谐和集中力下的积分形式解[J]. 水利学报, 1996(2):84-88.
WANG Lizhong, CHEN Yunmin, WU Shiming, et al. A solution to saturated elastic half-space under harmonic force of low frequency[J]. Journal of Hydraulic Engineering, 1996(2):84-88.
[7] 陈龙珠,陈胜立,梁发云. 饱和地基竖向振动的衰减特性[J]. 上海交通大学学报,2002,36(3):376-381.
CHEN Longzhu, CHEN Shengli, LIANG Fayun. Vibration attenuation of saturated strata by vertical surface loads[J]. Journal of Shanghai Jiaotong University, 2002,36(3):376-381.
[8] 杨峻, 吴世明. 弹性层和饱和半空间体系稳定动力响应[J]. 土木工程学报, 1997(3):39-48.
YANG Jun, WU Shiming. Steady state response of elastic soil layer and saturated layered half-space[J].China Civil Engineering Journal, 1997(3):39-48.
[9] 孙宏磊, 蔡袁强, 陈成振. 列车荷载作用下路轨系统及饱和弹性半空间上覆盖土层的动力响应[J]. 岩土工程学报, 2009, 31(6):922-928.
SUN Honglei, CAI Yuanqiang, CHEN Chengzhen. Dynamic response of railways on layered half-space subjected to moving train load[J].Chinese Journal of Geotechnical Engineering, 2009, 31(6):922-928.
[10] GRUNDMANN H, LIEB M, TROMMER E. The response of a layered half-space to traffic loads moving along its surface[J]. Archive of Applied Mechanics, 1999, 69(1):55-67.
[11] 刘洪波,刘洁,闻敏杰.深埋圆形隧洞非饱和土-衬砌结构系统的动力特性[J].振动与冲击,2016,35 (13):36-41.
LIU Hongbo,LIU Jie,WEN Minjie.Dynamic characteristics of unsaturated soil and lining system with a deeply embedded circular tunnel[J].Journal of Vibration and Shock,2016,35 (13):36-41.
[12] BRUTSAERT W. The propagation of elastic waves in unconsolidated unsaturated granular mediums[J]. Journal of Geophysical Research, 1964, 69(2): 243-257.
[13] 徐长节, 史焱永. 非饱和土中波的传播特性[J]. 岩土力学, 2004, 25(3):354-358.
XU Changjie, SHI Yanyong. Characteristics of wave propagation in unsaturated soils.[J]. Rock and Soil Mechanics, 2004, 25(3):354-358.
[14] VARDOULAKIS I, BESKOS D E. Dynamic behavior of nearly saturated porous media[J].Mechanics of Materials, 1986, 5(1): 87-108.
[15] 徐明江. 非饱和土地基与基础的动力响应研究[D]. 广州:华南理工大学,2009.
[16] 刘志军, 夏唐代, 黄睿,等. Biot理论与修正的Biot理论比较及讨论[J]. 振动与冲击, 2015,34(4):148-152.
LIU Zhijun, XIA Tangdai, HUANG Rui, et al. Comparison and discussion for Biot theory and modified Biot one[J].Journal of Vibration and Shock, 2015,34(4):148-152.
[17] BISHOP A W, ALPAN I, BLIGHT G E, et al. Fractors controlling the strength of partly saturated cohesive soils[C]//Research Conf on Shear Strength of Cohesive Soils. London, 1960.
[18] CAI Y, SUN H, XU C. Steady state responses of poroelastic half-space soil medium to a moving rectangular load[J]. International Journal of Solids and Structures, 2007,44(22): 7183-7196.
附录A

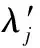
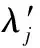

c45=μu(η2-ξ2)

c55=-λuξη+ξη(λu+2μu),

c65=λuξη-ξη(λu+2μu)(j=1,2,3,4);
d12=a32(iωbl-ω2ρl),d13=iωbl+a33(iωbl-ω2ρl),
d21=a41(iωbg-ω2ρg),d23=iωbg+a43(iωbg-ω2ρg),
d6=-μu(ξ2+η2)+d3,d7=-(ξ2+η2)-d11,
d8=-(ξ2+η2)-d22,d11=a31(iωbl-ω2ρl),
附录B

