基于应变振型的振动时效激振频率的确定方法与实验研究

顾邦平， 胡 雄， 杨振生， 赖金涛， 潘 龙(.上海海事大学 物流工程学院,上海 2006；2.绍兴文理学院 机械与电气工程学院,浙江 绍兴 2000；.浙江大学 浙江省先进制造技术重点实验室,杭州 0027)

消除构件加工制造过程中的残余应力是机械制造工业领域中的一项重要研究课题。振动时效技术因为具有设备简单、处理时间短、处理效果好等特点而成为备受关注的残余应力消除技术。国内外专家学者已经对振动时效工艺和理论开展了深入的研究[1-5]，并取得了丰富的理论成果和应用实例。通过国内外专家学者的研究发现，影响振动时效效果的关键工艺参数主要包括：激振频率、激振振幅和激振时间。目前对于激振频率的选择主要采用扫频法，即对构件进行扫频振动，寻找构件振动幅值较大的共振频率，然后在其共振频率或者亚共振频率下进行振动时效处理。然而通过扫频法确定振动时效的激振频率时，通常并不考虑材料的残余应力分布状态以及振型的分布规律，极大地限制了振动时效消除和均化残余应力的效果。

针对传统扫频法确定振动时效激振频率存在的不足，沈华龙等[6]在研究振动时效工艺时，采用有限元软件对构件进行数值模态分析，获取构件各阶位移振型和模态频率，然后根据振型的分布规律指导振动时效的现场试验，取得了不错的效果。然而构件的位移振型相对于应变振型对构件的局部变化并不敏感，并不能直接去研究构件某些关键部位的应变分布[7-9]，并且构件的高阶应变振型对构件的局部变化相对于低阶应变振型更加敏感。此外，国内外专家学者也对激振频率大于1 kHz的高频振动时效[10-11]和超声振动时效[12-13]开展了相关的研究。因此获取构件的应变振型能够更准确的反映振动能量在构件表面的分布规律，这对于指导振动时效的现场试验是有益的。

本文采用ANSYS有限元软件，对构件进行数值模态分析，通过分析应变振型和残余应力的分布规律，确定了基于应变振型的振动时效激振频率的确定方法和步骤，并通过实验验证该方法的提出对振动时效效果改善的有效性。

1 数值模态分析

1.1 应变振型控制方程的推导

文中将以位移振型为基础，推导应变振型与位移振型的关系，建立应变振型的控制方程，为后续的数值模态分析奠定基础。一个典型的有限单元是由节点j，k，m和相应的连接直线来定义的，则该单元内任意一点的位移ui可以表示为[14]

ui=Niai

(1)

式中：Ni是基于节点位置事先给定的函数，称为形状函数矩阵;ai表示第i个单元所有节点位移组成的节点位移向量。

当已知单元内任意位置的位移，则相应的可以确定出单元内任意位置的应变εi，其表达式为

εi=Siui

(2)

式中：Si为微分算子矩阵。若系统被划分为n个单元，则共有n个式(2)这样的方程，可以表示为

(3)

可以简写为

ε=Su

(4)

式中：ε为n个单元的应变向量;u为n个单元的节点位移向量。式(4)建立的应变与位移的关系是在单元坐标系中建立的，考虑到各单元在连接节点上位移是连续变化的，则单元节点位移向量可以通过式(5)的坐标变换转换到总体坐标系中

u=Tug

(5)

式中：T为坐标变换矩阵;ug为在总体坐标系中的节点位移向量。将式(5)代入式(4)中，可以得到总体坐标系中的应变方程为

(6)

采用有限元模型，在总体坐标系中，系统的无阻尼运动方程为

(7)

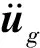
(Kg-ω2M)Umax=Fmax

(8)

采用模态叠加法，节点位移的响应可以表示为

Umax=φYφTFmax

(9)

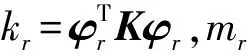
将式(9)代入到式(6)中，可以得到

(10)

令ψ=STφ，对位移振型进行微分运算可以得到应变振型，而矩阵S为微分算子，因此ψ称为应变模态振型矩阵，ψr为第r阶应变模态振型，与第r阶位移模态振型φr相对应。从能量的角度，第r阶应变模态振型反应的是构件第r阶固有能量分布状态，与固有频率和位移模态振型一样也是反映构件固有特性的一个参数。

1.2 模型建立及材料设置

物理模型：数值模态分析的试件为后续实验中采用的45#钢板状构件，长230 mm，宽210 mm、厚6 mm，如图1所示。为了研究构件局部结构的变化对其位移振型和应变振型的影响，对两种结构的板状构件进行数值模态分析，其中板状构件1#的中心无通孔，称为无孔构件，另外一板状构件2#的中心有φ6 mm的通孔，称为有孔构件。由于数值模态分析的构件三维几何模型相对简单，此处选择直接在ANSYS经典GUI界面中建立构件的三维几何模型。

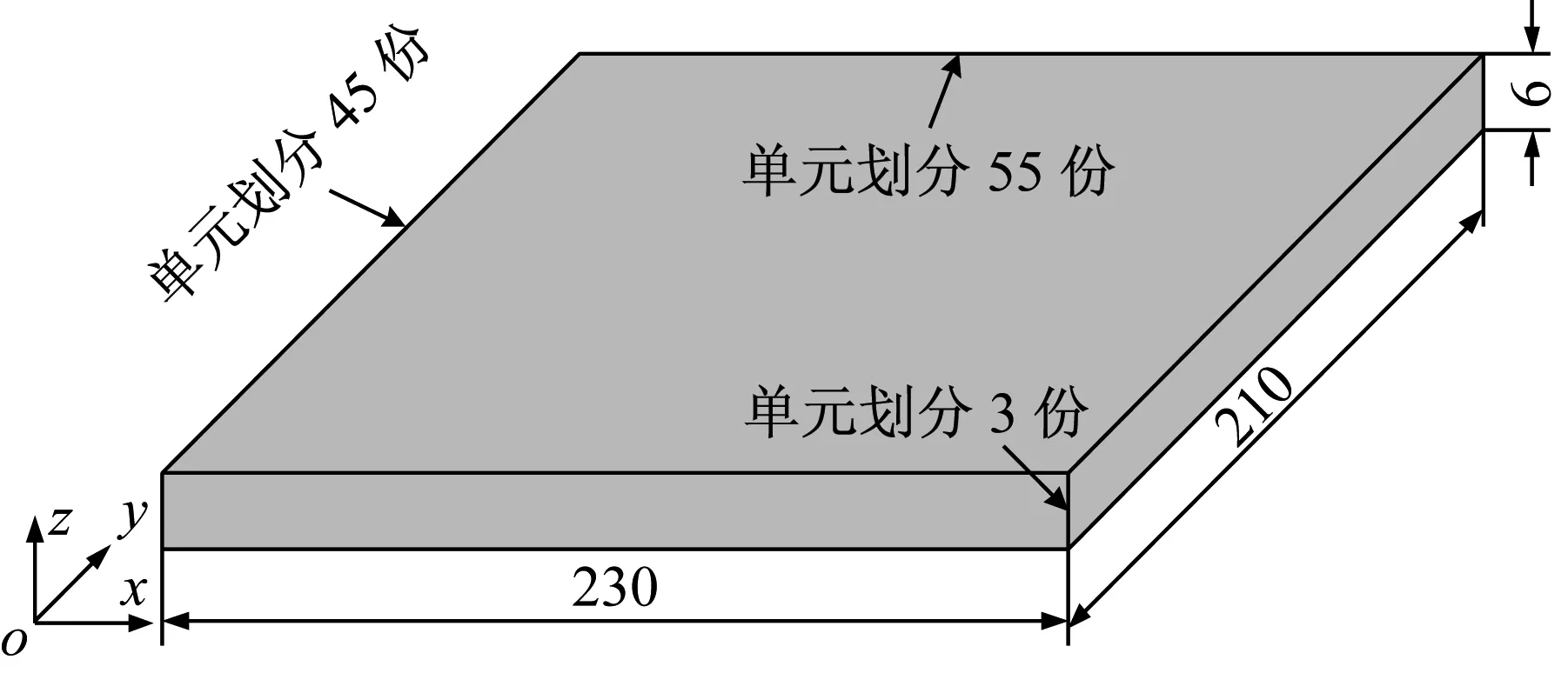
图1 数值分析构件示意图(mm)

Fig.1 Schematic of the workpiece used in the numerical analysis(mm)

材料设置：数值模态分析时需要用到45#钢的密度ρ、弹性模量E、泊松比ν，具体数值分别为ρ=7 850 kg/m3、E=200 GPa、ν=0.28。

有限元模型：采用20节点的SOLID95单元对构件划分网格，建立其三维有限元模型。为了提高求解的精度，在试件的长度、宽度以及厚度三个方向设置单元划分的数目分别为55、45以及3，如图1所示。然后采用扫掠(Volume Sweep)的方式对构件划分网格，可以得到规则的网格，也可以提高求解的精度。另外，SOLID95单元具有中间节点，这将使得求解的结果更为精确。

1.3 求解方法

采用ANSYS模态分析模块中的Block Lanczos方法(分块兰索斯法)求解构件的位移模态振型和应变模态振型。Block Lanczos法特征值求解器是ANSYS模态分析模块中的默认求解器，采用的是Lanczos算法。这种算法不仅可以保证求解的精确性，更能提高求解的速度。

1.4 数值结果及分析

采用1.3小节的求解方法求解1.1小节建立的位移模态和应变模态的控制方程可以获得构件的位移模态和应变模态的数值结果。无孔构件低阶模态振型(模态频率为572 Hz)如图2所示，其中图2(a)为其位移振型，图2(b)为其应变振型；有孔构件低阶模态振型(模态频率为571 Hz)如图3所示，其中图3(a)为其位移振型，图3(b)为其应变振型。

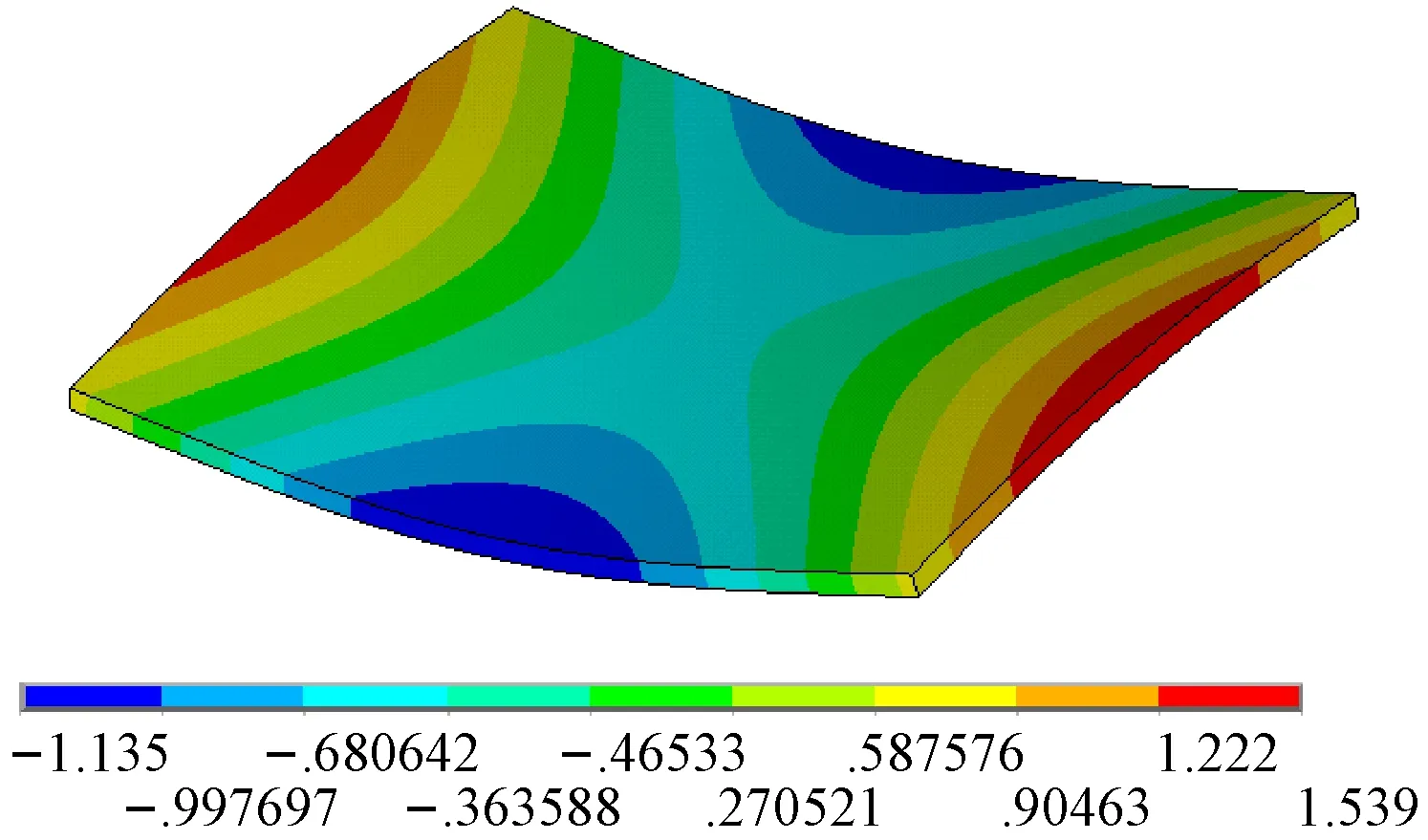
(a) 位移振型

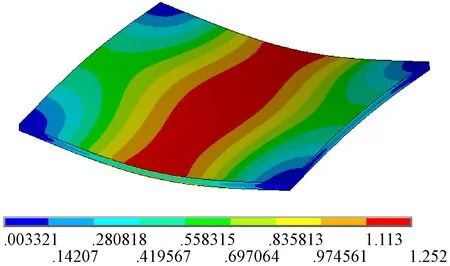
(b) 应变振型图2 无孔构件低阶模态振型(572 Hz)

Fig.2 Low order modal mode of the workpiece without the hole (572 Hz)

无孔构件高阶模态振型(模态频率为3 231 Hz)如图4所示，其中图4(a)为其位移振型，图4(b)为其应变振型；有孔构件高阶模态振型(模态频率为3 229 Hz)如图5所示，其中图5(a)为其位移振型，图5(b)为其应变振型。

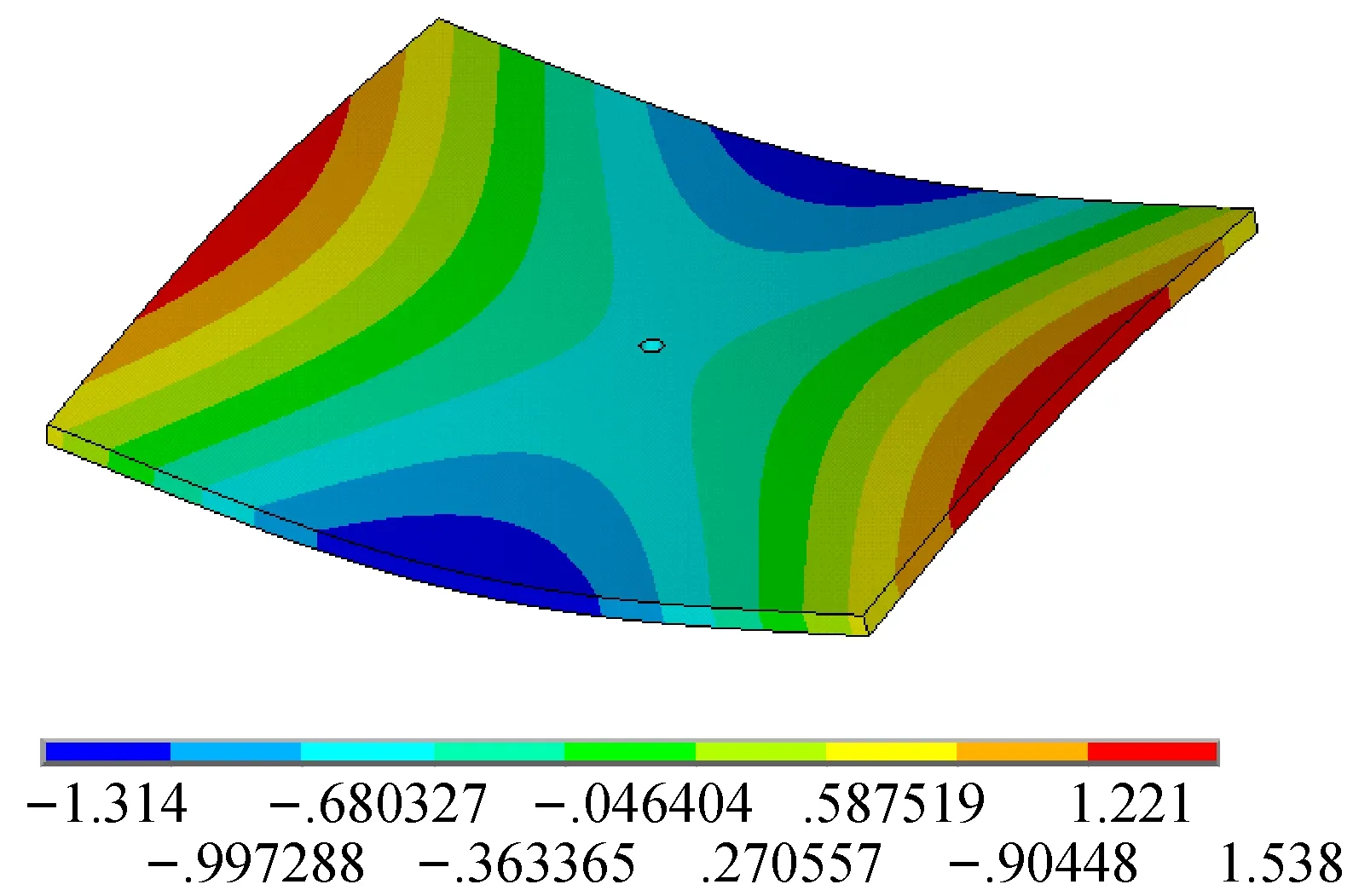
(a) 位移振型

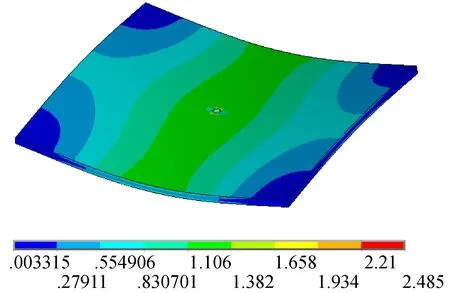
(b) 应变振型图3 有孔构件低阶模态振型(571 Hz)

Fig.3 Low order modal mode of the workpiece with the hole (571 Hz)

(a) 位移振型

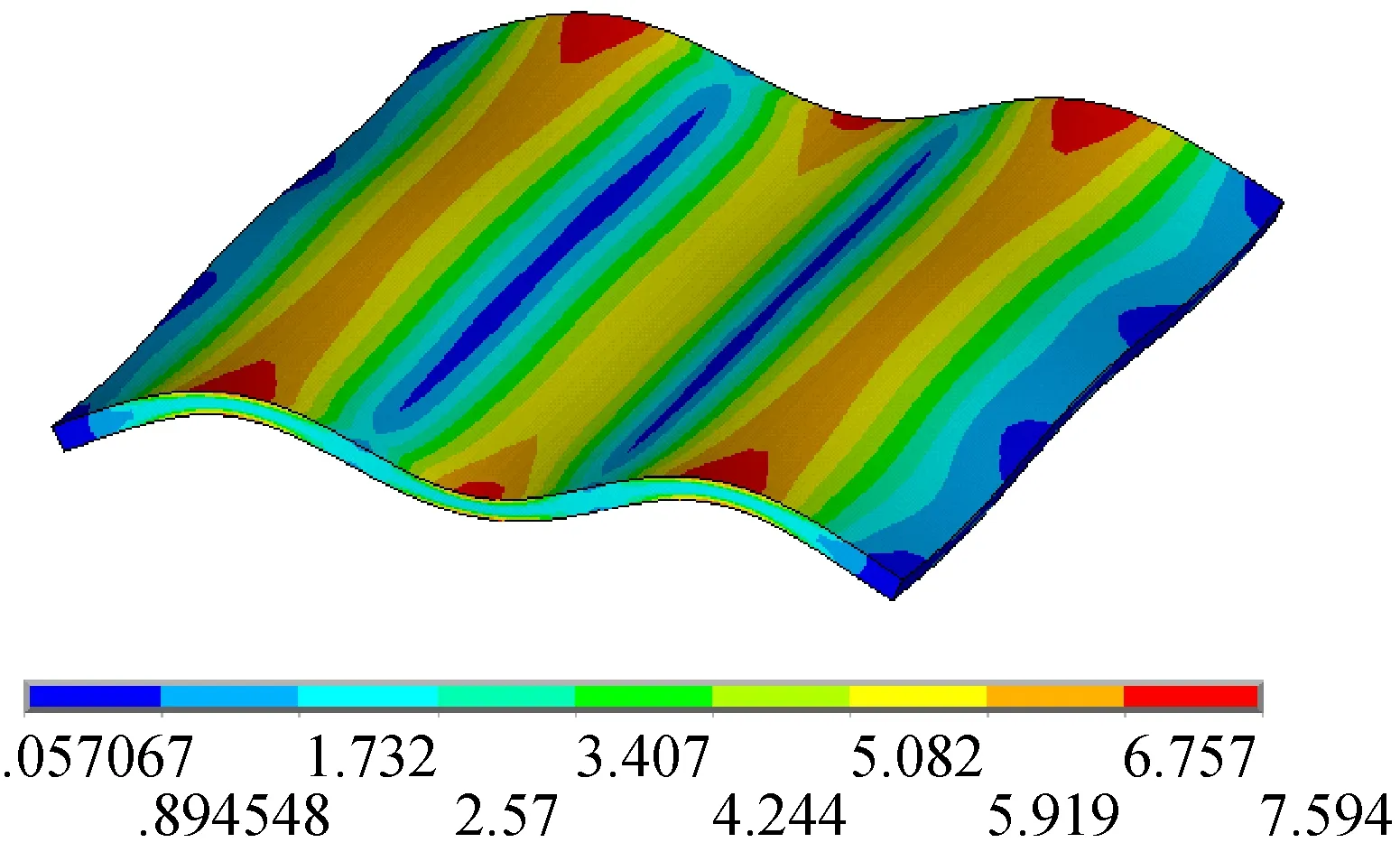
(b) 应变振型图4 无孔构件高阶模态振型(3 231 Hz)Fig.4 High order modal mode of the workpiece without the hole(3 231 Hz)

(a) 位移振型

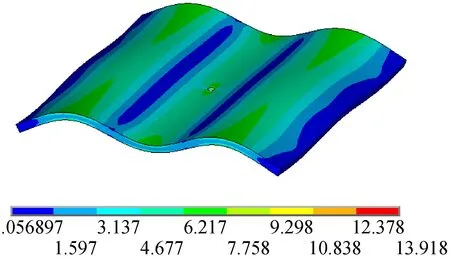
(b) 应变振型图5 有孔构件高阶模态振型(3 229 Hz)Fig.5 High order modal mode of the workpiece with the hole(3 229 Hz)

对比无孔构件和有孔构件的位移振型和应变振型，可以发现构件局部结构的变化在其低阶和高阶应变振型上都能够得以体现，而低阶和高阶位移振型对于构件局部结构的变化都不敏感，同时从构件的应变振型上可以直观地看出构件各部分分布的动应变的大小，有利于直观地评估构件各部分残余应力的释放效果，这说明了为什么从应变振型的角度探讨振动时效激振频率的确定方法。

扫频法是目前常用的确定振动时效激振频率的方法，即对构件进行扫频振动，寻找构件的共振频率，然后在共振频率下对构件进行振动时效处理。然而这种方法确定的激振频率并未考虑到构件表面的残余应力分布状态和共振频率所对应的应变振型，这极大地降低了振动时效的效果。从图3(b)和图5(b)的应变振型分布规律可知，高阶应变振型具有较多的应变峰值，更有利于消除残余应力分布状态复杂的构件的残余应力。假如构件表面的峰值残余应力主要分布在图3(b)所示的应变峰值附近，此时选取图3(b)应变振型所对应的模态频率进行振动时效处理能够获得较为理想的振动时效效果。若构件表面的峰值残余应力分布在图5(b)所示的两个应变峰值附近，此时选取图5(b)应变振型所对应的模态频率进行振动时效处理能够获得较为理想的振动时效效果。从上面的分析，我们不难发现对于振动时效的激振频率的确定，不仅要考虑构件表面的残余应力分布状态，而且需要考虑构件的应变振型，两者缺一不可。因此，为了提高振动时效效果，对于激振频率f的选择应以构件表面的残余应力分布为依据，共振应变函数ψr为准则。

在此基础上本文提出了基于应变振型的振动时效激振频率的确定方法，其步骤主要包括：①获取构件表面的残余应力分布状态；②建立构件的有限元模型，对构件进行数值模态分析；③获取构件的各阶应变振型和模态频率；④在步骤①和③的基础上，初步确定振动时效的激振频率；⑤以数值模态分析确定的激振频率为基础，在其一定范围内对构件进行扫频振动，获取振动幅值较大的频率作为振动时效的激振频率。通过本文提出的方法确定的激振频率是以构件表面的残余应力分布为依据，共振应变函数ψr为准则的，有利于获得较为理想的振动时效效果。

2 实验研究

2.1 实验材料

碳素结构钢被广泛应用于工程结构中，这种材料在实际应用中由于存在较大的残余应力而经常产生损伤破坏，特别是在有些场合不允许采用热时效对其进行去应力处理，因此有必要尝试采用振动时效对碳素结构钢的残余应力进行消除研究。实验中选用45#优质碳素结构钢来制备实验试样。

2.2 试样制备

实验试样(即1.2小节数值模态分析的试件)的尺寸为230 mm×210 mm×6 mm，如图1所示。为了使得试样的表面产生较大的拉伸残余应力，实验中采用激光表面处理工艺来产生残余应力。这种工艺是通过激光与试样相互作用区域快速的升温来改变试样的微观组织形态，试样的表面产生热损伤而产生初始拉伸残余应力。激光表面处理工艺在SLC-2030D龙门式CO2多功能激光加工机上展开，激光器的型号为Rofin SLAB DC030。原理图如图6所示。

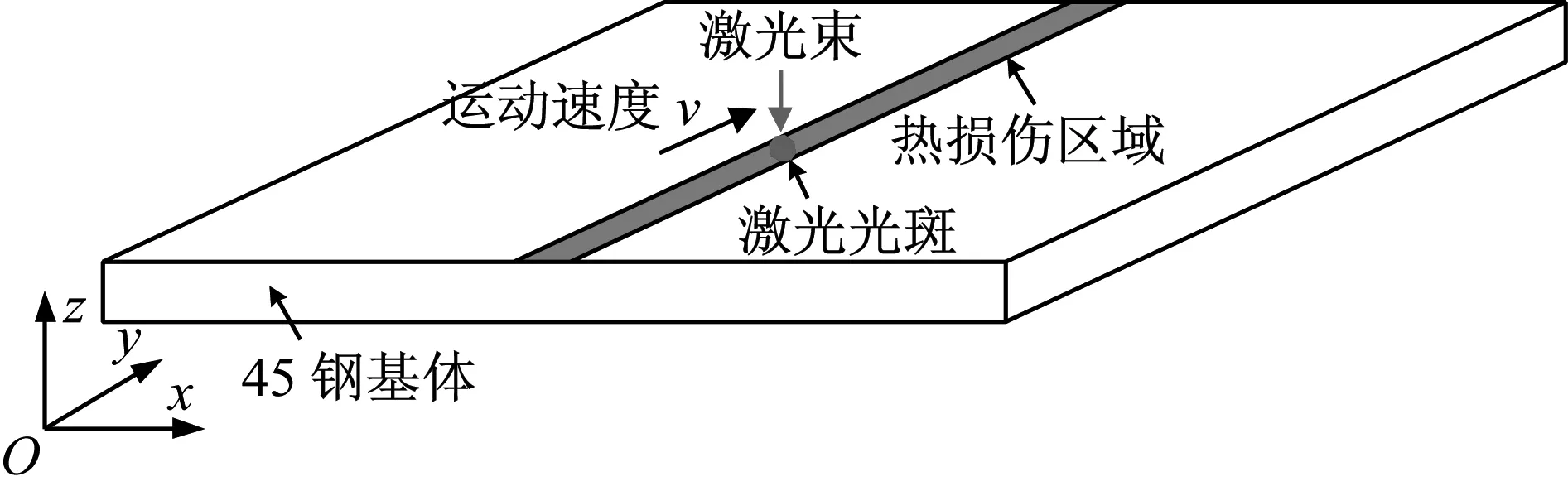
图6 激光表面处理工艺的原理图Fig.6 Schematic of the laser surface processing

2.3 小孔法评估残余应力

试样残余应力测点以及应变花粘贴方向如图7所示。实验中对试样的两个区域进行激光表面处理，每个激光热损伤区域的中心距离试样的边缘均为55 mm。实验中选取14个测点用于评价振动前后试样的残余应力，其中测点1#～7#被分为一组，用于测试振动前试样的残余应力，测点1′#～7′#被分为另一组，用于测试振动后试样的残余应力。每一组测点对称的分布在垂直于垂直中心线的直线上，距离垂直中心线的距离分别为0、40 mm、60 mm、80 mm，每组测点距离试样边缘的距离均为80 mm。以测点4为例，其应变花的粘贴方向如图7所示，其余测点处应变花的粘贴方向与测点4处应变花的粘贴方向一致。通过应变仪测试试样钻孔处的释放应变ε1、ε2、ε3，并将释放应变代入如下的方程就可以求解出试样钻孔处x轴向和y轴向的残余应力σx和σy

(11)

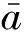
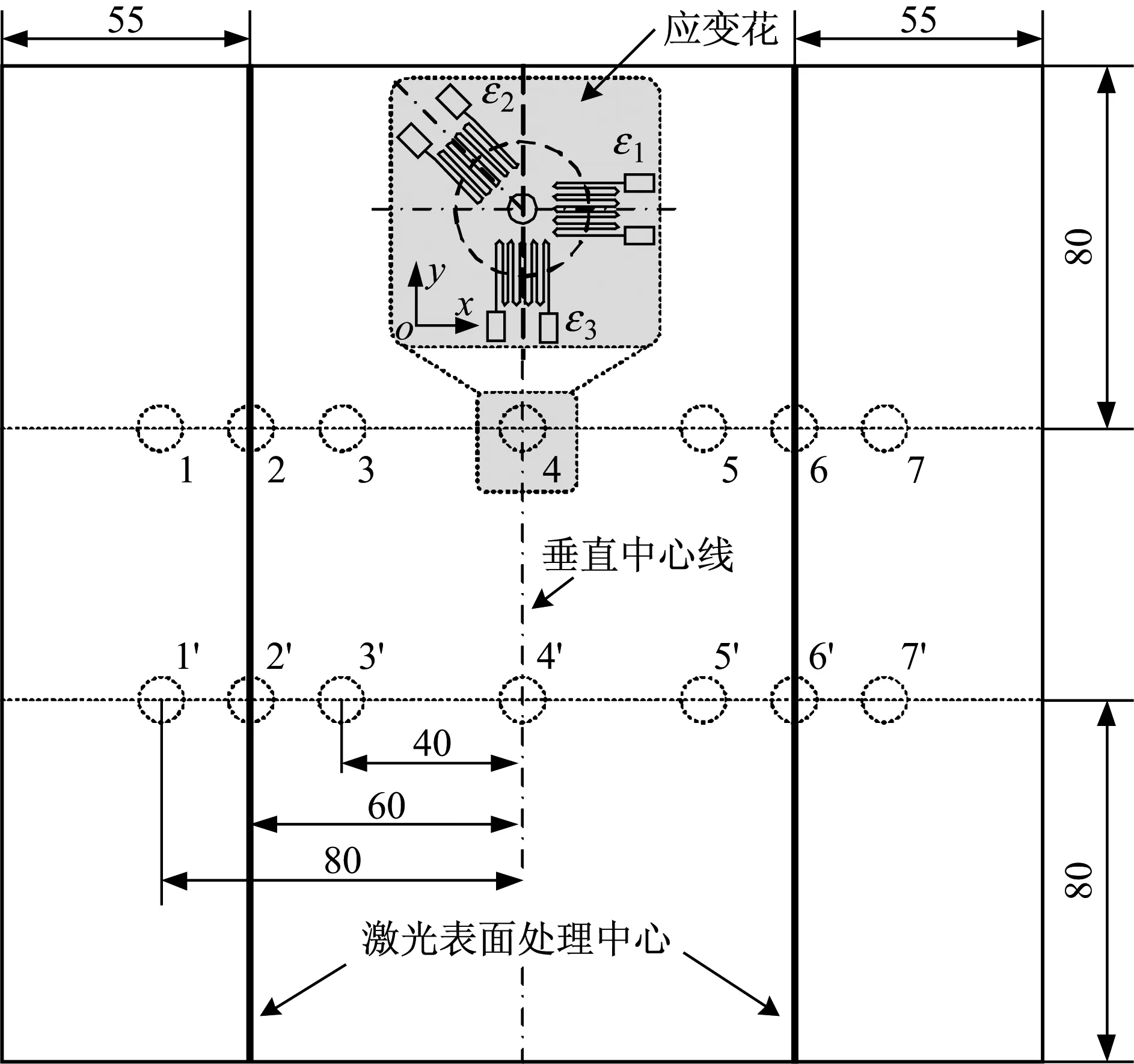
图7 残余应力测点示意图(mm)Fig.7 Schematic of the measured points for residual stress(mm)

2.4 振动时效过程

振动时效实验装置主要包括：电磁式激振器、高频振动能量放大装置、信号发生器、功率放大器、压电式加速度传感器、电荷放大器、示波器。首先，将试样通过安装孔装夹在高频振动能量放大装置上；然后，按照本文提出的方法对试样进行扫频振动，发现试样在频率717 Hz处有一个峰值较大的共振频率点，以及在频率3 311 Hz处有一个峰值较大的共振频率点；最后，对其中一件试样(称为1#试样)在频率717 Hz处进行振动时效处理，对另一件试样(称为2#试样)在频率3 311 Hz处进行振动时效处理。

2.5 实验结果及分析

图8为振动时效前后1#试样x轴向和y轴向的残余应力测试结果。图9为振动时效前后2#试样x轴向和y轴向的残余应力测试结果。

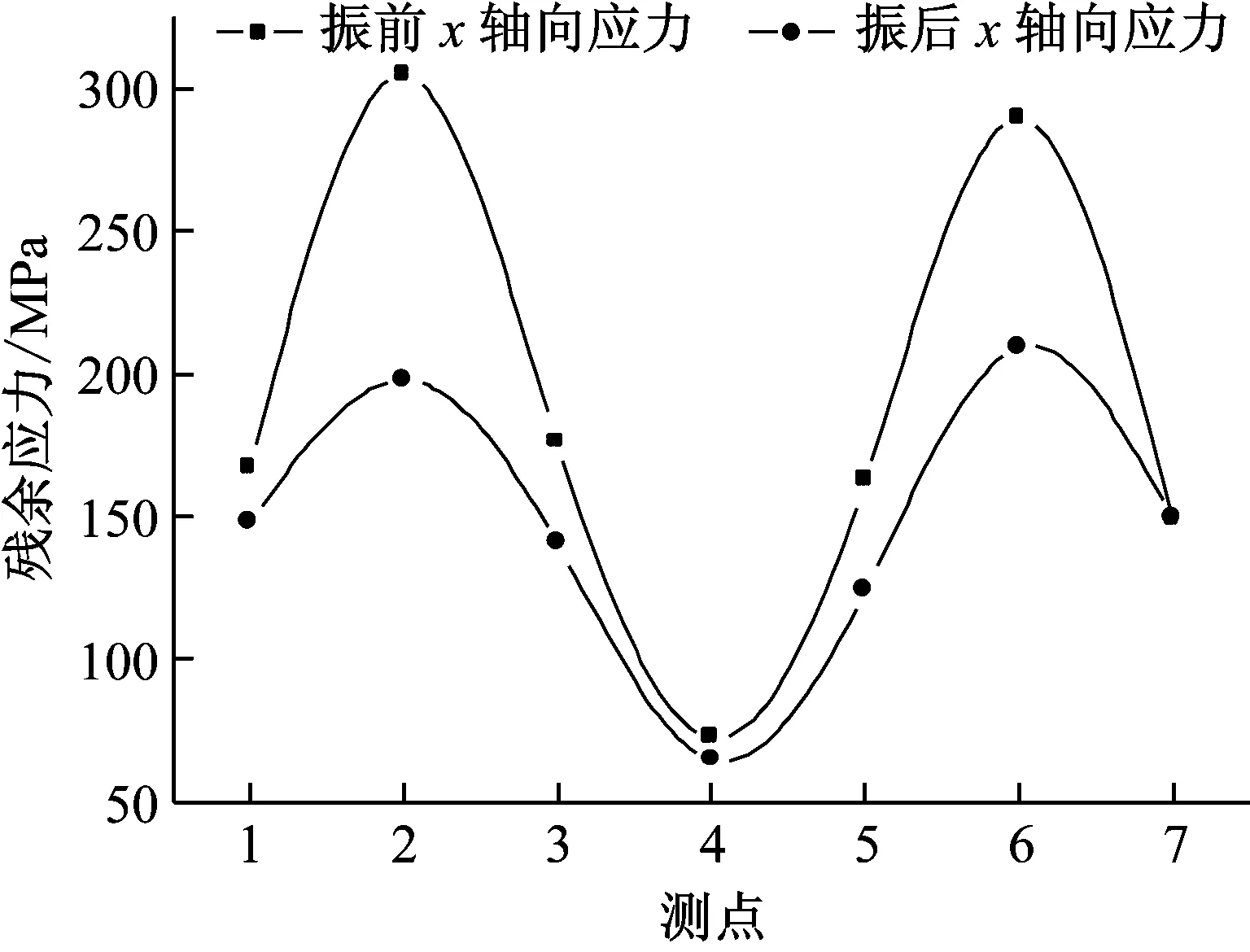
(a) x轴向残余应力

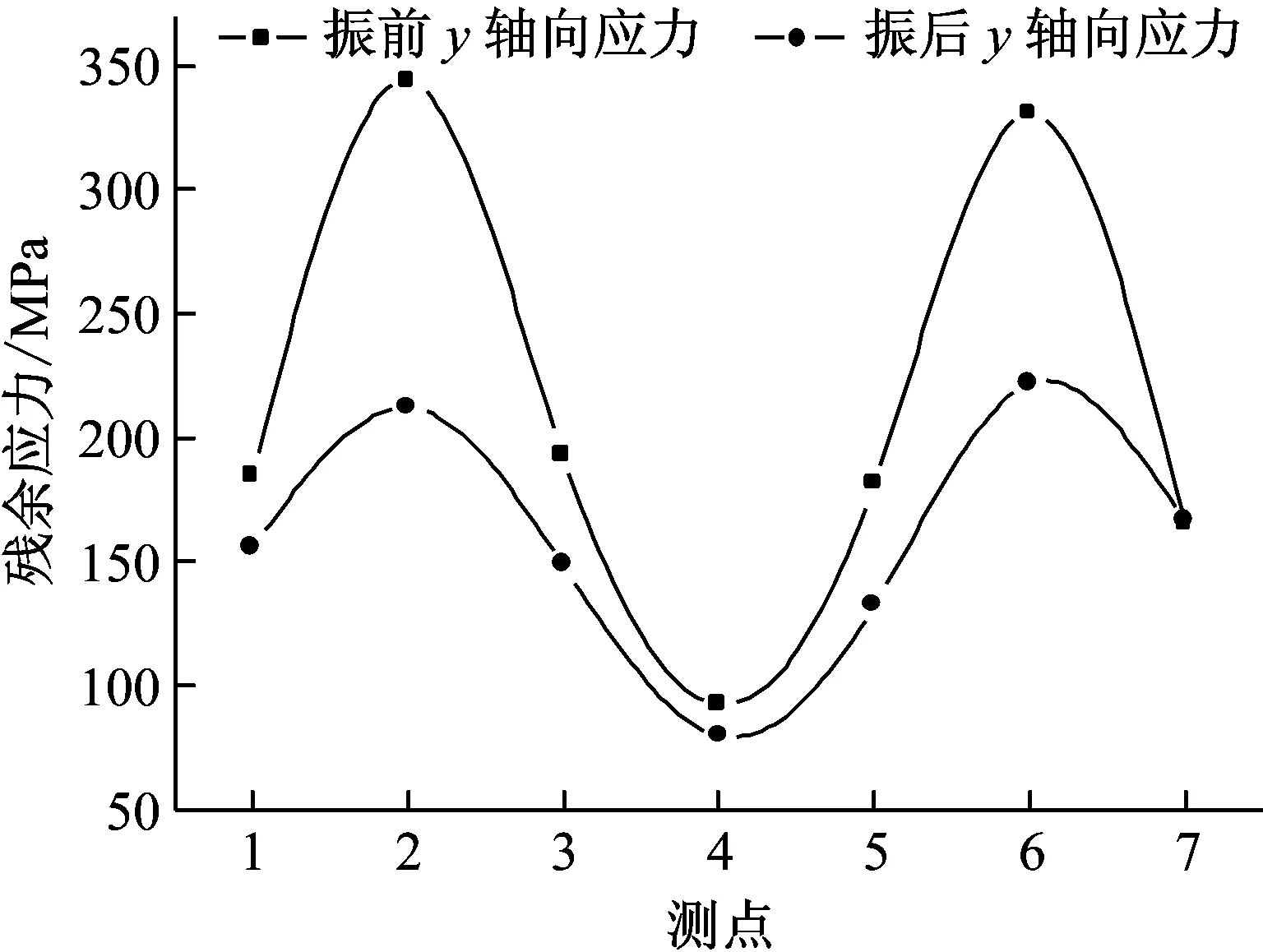
(b) y轴向残余应力图8 振动时效前后1#试样残余应力测试结果

Fig.8 Residual stress measuring results of 1# specimen before and after the vibratory stress relief

1#试样和2#试样振动前残余应力的测试结果表明，试样最大的残余应力出现在激光表面烧伤处理中心区域，随着远离激光表面烧伤中心区域距离的增加，残余应力则逐渐降低。1#试样和2#试样振动时效处理后残余应力峰值消除率均较大，而对于残余应力较小的地方(远离激光表面烧伤中心区域)，振动时效处理后残余应力的消除率相对较小。由图8可见，1#试样经过振动时效处理后其x轴向和y轴向峰值残余应力的释放量分别为106.8 MPa和131.8 MPa；由图9可见，2#试样经过振动时效处理后其x轴向和y轴向峰值残余应力的释放量分别为183.6 MPa和226.1 MPa，表明根据残余应力分布状态和应变振型分布规律，合理的选择振动时效的激振频率能够获得较为理想的振动时效消除残余应力效果。

由图8和图9可见，2#试样具有更好的振后残余应力均化分布效果，表明根据残余应力分布状态和应变振型分布规律，合理的选择振动时效的激振频率，可以获得较为理想的振动时效均化残余应力效果。何闻等学者在文献[3]中研究指出对试样在较高的频率下激振，试样上分布较多的应变峰值，并且动应变在试样上的分布更加均匀，提高了试样表面的残余应力均化效果；除此以外，通过1.4小节对试样应变振型的分析结果和2.5小节的残余应力测试结果可知，2#试样的残余应力峰值分布在其应变振型峰值的附近，所以2#试样具有更好的残余应力均化效果。综上所述，对于构件进行振动时效处理时，需要根据构件表面的残余应力分布状态和应变振型分布规律，合理选取振动时效的激振频率，能够获得较为理想的振动时效消除和均化残余应力效果。

(a) x轴向残余应力

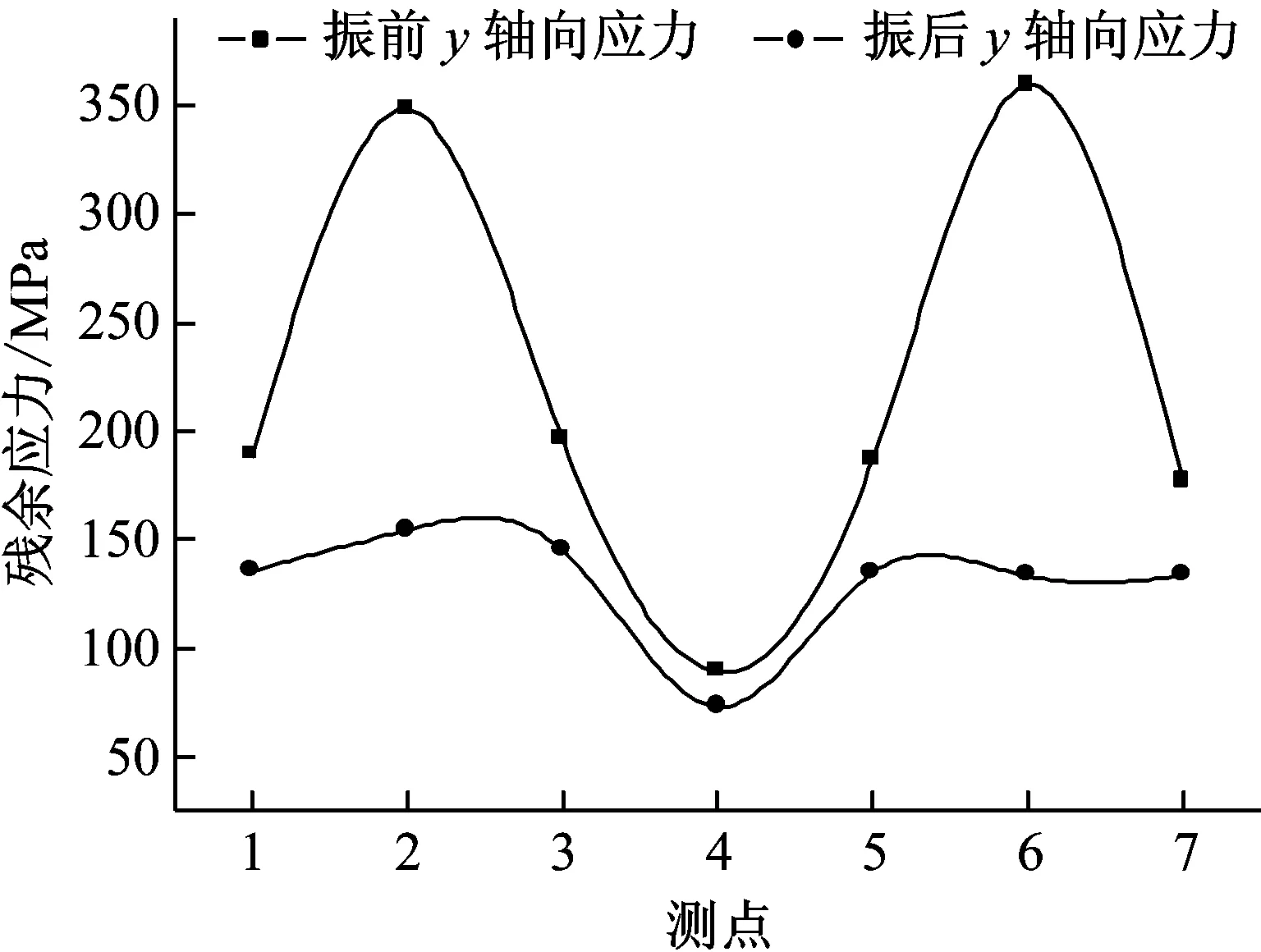
(b) y轴向残余应力图9 振动时效前后2#试样残余应力测试结果

Fig.9 Residual stress measuring results of 2# specimen before and after the vibratory stress relief

3 结 论

(1)通过分析应变振型和残余应力的分布规律，得到了基于应变振型的振动时效激振频率的确定准则，即为了提高振动时效的效果，对于激振频率f的选择应以构件表面的残余应力分布为依据，共振应变函数ψr为准则。

(2)基于应变振型的振动时效激振频率的确定方法，其步骤主要包括：①获取构件表面的残余应力分布状态；②建立构件的有限元模型，对构件进行数值模态分析；③获取构件的各阶应变振型和模态频率；④在步骤①和③的基础上，初步确定振动时效的激振频率；⑤以数值模态分析确定的激振频率为基础，在其一定范围内对构件进行扫频振动，获取振动幅值较大的频率作为振动时效的激振频率。

(3)1#试样经过振动时效处理后其x轴向和y轴向峰值残余应力的释放量分别为106.8 MPa和131.8 MPa；2#试样经过振动时效处理后其x轴向和y轴向峰值残余应力的释放量分别为183.6 MPa和226.1 MPa，表明根据残余应力分布状态和应变振型分布规律，合理的选择振动时效的激振频率能够获得较为理想的振动时效效果。

参 考 文 献

[1] WALKER C A, WADDELL A J, JOHNSTON D J. Vibratory stress relief-an investigation of the underlying process[J]. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 1995, 209:51-58.

[2] KWOFIE S. Plasticity model for simulation, description and evaluation of vibratory stress relief[J]. Materials Science and Engineering A, 2009, 516:154-161.

[3] 蒋刚, 何闻, 郑建毅. 高频振动时效的机理与实验研究[J]. 浙江大学学报(工学版), 2009, 43(7):1269-1272.

JIANG Gang, HE Wen, ZHENG Jiangyi. Mechanism and experimental research on high frequency vibratory stress relief[J]. Journal of Zhejiang University (Engineering Science), 2009, 43(7):1269-1272.

[4] 刘晓丹, 陶兴华, 韩振强. 振动时效工艺在消除膨胀波纹管残余应力中的应用[J]. 振动与冲击, 2015, 34(4):171-174.

LIU Xiaodan, TAO Xinghua, HAN Zhenqiang. Application of vibratory stress relief in relaxation of residual stress for expandable corrugated liners[J]. Journal of Vibration and Shock, 2015, 34(4):171-174.

[5] 韩衍昭, 刘爱敏. 振动时效工艺参数选取的探讨[J]. 热加工工艺, 2012, 41(16):189-191.

HAN Yanzhao, LIU Aimin. Discussion on selection of technology parameters for vibration stress relief[J]. Hot Working Technology, 2012, 41(16):189-191.

[6] 沈华龙, 吴运新, 郭俊康. 高强度铝合金厚板振动时效工艺的研究[J]. 振动与冲击, 2009, 28(8):191-194.

SHEN Hualong, WU Yunxin, GUO Junkang. VSR technology used in high intensity aluminum alloy thick plates[J]. Journal of Vibration and Shock, 2009, 28(8):191-194.

[7] 李德葆, 陆秋海. 实验模态分析及其应用[M]. 北京: 科学出版社, 2001.

[8] YAM L H, LEUNG T P, LI D B, et al. Theoretical and experimental study of modal strain analysis[J]. Journal of Sound and Vibration, 1996, 191(2):251-260.

[9] 徐丽, 易伟建. 应变模态在框架结构节点损伤诊断中的应用研究[J]. 振动、测试与诊断, 2006, 26(2):102-107.

XU Li, YI Weijian. Damage detection of frame structure joints using strain modal method[J]. Journal of Vibration Measurement & Diagnosis, 2006, 26(2):102-107.

[10] HE W, REN Y, CHEN C, et al. Analysis on technology of high-frequency vibratory stress relief[C]∥Proceedings of 2005 ASME Power Conference. Chicago, IL, 2005.

[11] HE Wen, GU Bangping, ZHENG Jianyi, et al. Research on high-frequency vibratory stress relief of small Cr12MoV quenched specimens[J]. Applied Mechanics and Materials, 2012, 157/158:1157-1161.

[12] SHALVANDI M, HOJJAT Y, ABDULLAH A, et al. Influence of ultrasonic stress relief on stainless steel 316 specimens: a comparison with thermal stress relief[J]. Materials and Design, 2013, 46:713-723.

[13] 王壬炎, 王时英. 超声振动时效的机理及实验研究[J]. 中国农机化学报, 2015, 36(2):59-62.

WANG Renyan, WANG Shiying. Mechanism analysis and experimental research of the ultrasonic vibration aging[J]. Journal of Chinese Agricultural Mechanization, 2015, 36(2):59-62.

[14] ZIENKIEWICZ O C, TAYLOR R L. 有限元方法基本原理(第1卷)[M]. 曾攀,等,译. 北京: 清华大学出版社, 2008.

[15] American Society for Testing and Materials. ASTM E 837-08 Standard test method for determining residual stresses by the hole-drilling strain-gage method[S]. Pennsylvania: ASTM International, 2008.