嵌入式传感器的齿轮裂纹故障诊断

宁少慧， 韩振南， 武学峰， 王志坚(.太原科技大学 机械工程学院,太原 0004；.太原理工大学 机械工程学院,太原 0004；.中北大学 机械与动力工程学院,太原 0005)

在齿轮传动系统的故障诊断中，常用的诊断方法是分析齿轮箱体上的振动信号来判断传动系统是否正常工作。为了从箱体振动信号中提取故障特征，很多学者研究了多种信号处理方法[1-5]。但安装在轴承座表面或箱体靠近轴承的传感器所采集振动信号有明显的不足：当齿轮发生点蚀，裂纹等早期故障时，齿轮啮合点到传感器的振动传输路径周期性变化，信号在传递过程中会造成能量损失，导致信号被削弱，信噪比低，齿轮早期的微弱的故障信号很难提取到。因此，嵌入式诊断成为一种新的故障诊断方法。

嵌入式诊断技术是由美军提出的一种新思想[6]，它是在装备内部嵌入智能微传感器。陈仲生等[7]使用振动传递符号有向图和粒子群优化，研究了齿轮箱嵌入式传感器优化配置模型；Smith等[8-9]把传感器安装在行星齿轮箱内的保持架上，成功诊断出了轴承的内圈故障。对于嵌入式故障诊断系统，传感器可以嵌入到轴承、齿轮和齿轮轴等零件中，故障信号会随着传递路径的增加和经过零件数目的增多而衰减。对于一级圆柱齿轮减速器的传动系统，当传感器安装在箱体上时，啮合点与传感器之间的传递路径：故障信号通过齿轮体-齿轮轴-轴承-箱体-传感器。本文提出把传感器安装在离故障源较近的齿轮体上的传递路径是：故障信号通过齿轮体-传感器，这样振动信号的传递路径大大缩短，有效降低传递过程的衰减和各种干扰，提高振动信号的信噪比。有限元分析软件ANSYS/LS-DYNA适用于齿轮传动系统动力学仿真分析[10-11]。本文通过LS-DYNA建立了齿轮传动系统动力学模型，仿真分析了系统的不同零件上的振动加速度信号，说明了振动信号在传递过程中的衰减以及频率成分的损失，又分析了齿轮传动系统实验数据，验证了该方法的有效性。

1 ANSYS/LS-DYNA显示动力学

有限元动力学分析一般采用显式算法，因为求解动力学方程时采用差分格式,既不需要直接求解切线刚度，也不需要进行平衡迭代，所以计算速度快，因此，采用显式动力学方法对齿轮传动系统进行动力学分析。在动力学有限元分析中,系统的求解方程式为[12]

(1)

LS-DYNA采用显式中心差分法来解这个运动方程，在已知t1…tn-1时间步解的情况下，求解tn时间步的解，运动方程为

(2)

(3)

但是对于显式中心差分法积分，满足收敛的临界时间必须满足下式

Δt≤Δtcr=2/ωmax

(4)

式中：Δtcr为临界时间步长，ωmax为有限元网格的最大自然角频率，由系统中最小单元的特征值方程|Kn-ω2Mn|=0得到。为保证收敛，LS-DYNA采用变步长积分法，每一时刻的积分步长由当前构型中的最小单元决定。

2 齿轮传动系统动力学仿真分析

2.1 有限元模型的建立

齿轮传动系统的参数：主动轮齿数是30，从动轮齿数为45，模数是4 mm，压力角为20°，中心距是150 mm。为了得到精确的齿轮动态响应,接触处网格划分更密些。在LS-DYNA显示动力学分析中，采用单元类型有SOLID164三维实体单元和SHELL163壳单元，SOLID164不具有旋转方向的自由度，用于实体网格的划分。SHELL163用来划分齿轮内孔，模拟齿轮系统的旋转。建立的齿轮系统的有限元模型如图1所示。

图1 齿轮传动系统有限元模型Fig.1 Finite element model of gear transmission system

2.2 仿真分析中裂纹的处理

在有限元动力学分析中，如何合理模拟齿轮齿根处的裂纹至关重要。在划分网格之前首先应该在沿着齿宽方向的齿根处切除掉一个扁小的三棱柱，缺口部分代表裂纹，去掉一部分材料仅使轮齿具有裂纹的外观，关键是要使裂纹处具有真实裂纹的特性，这就要求对裂纹前缘处的网格进行单元奇异化处理，反映裂纹处的特性。

本文使用标准六节点三角形单元，如图2所示，这种网格单元可以使应力分布具有奇异特性[13]。把裂纹前缘的单元全部进行奇异化处理，使之具有裂纹应力特性，更加接近真实结果。仿真时把从动轮设为故障齿轮，在从动轮的齿根处切割出裂纹，长度为2 mm，贯穿全齿，如图3。

图2 裂纹尖端点周围的单元Fig.2 Element around the crack tip

图3 齿轮裂纹有限元模型Fig.3 Finite element model of gear crack

2.3 传动系统的边界条件设置

根据系统的实际工作条件,其动力学分析的边界条件如下：

(1)接触设置。利用关键字CONTACT设置两齿轮间为面面接触,定义其静摩擦因数为0.23，动摩擦因数为0.16[14]。

(2)在主动轮的内圈以曲线的形式加载转速，模拟系统输入端转速。在从动轮的内圈加阻碍转动的阻力矩，模拟系统输出端所承受的负载。从动轮加载400 Nm扭矩，主动轮加载126 rad/s的转速(1 200 r/min)，为了解决突变载荷造成的系统振荡问题，计算中转速和负载力矩分别在0.02 s内由零逐渐增加至最大值。加载曲线如图4所示。

(3)在轴承外圈节点上施加全约束,模拟轴承座对轴承的约束。

(4)求解参数的设置。本文中求解终止时间设置为0.3 s。

(a)转速(b)负载力矩

图4 齿轮系统载荷边界条件

Fig.4 Load boundary conditions of gear transmission systems

2.4 仿真结果

图5和图6分别是齿轮传动系统无故障和裂纹故障的振动信号时域图。分别从齿轮传动系统中齿轮体，齿轮轴和轴承上提取相应的加速度振动信号，可以看出，随着振动路径的加长，振动信号在传递过程出现振幅衰减和频率成分的损失。无故障信号的时域波形图存在周期性的波动，而裂纹信号存在较大的脉冲，并且脉冲的频率f=1/Δt=13 Hz恰为裂纹齿轮所在轴的转频。从图6中还可以发现，脉冲频率只出现在齿轮体和齿轮轴的振动信号中，而在轴承上的信号中并没出现。这说明在齿轮传动系统中出现的早期故障从箱体上的振动信号中很难被发现，而安装在齿轮体上的传感器的振动信号则能明显的反映出齿轮是否出现故障。

(a) 轮体

(b) 齿轮轴

(c) 轴承图5 健康齿轮系统时域振动信号Fig.5 Time-domain signalsof healthy gear system

(a) 轮体

(b) 齿轮轴

(c) 轴承图6 故障齿轮系统时域振动信号Fig.6 Time-domain signalsgearsystem with the 2 mm crack

3 齿轮传动系统实验装置

3.1 齿轮传动实验系统

单级齿轮传动实验系统如图7所示，由电机驱动整个传动系统的运转，通过扭力杆加载，从扭矩测量仪观察转速和力矩的大小。传感器上的振动信号通过信号采集系统采集并通过MATLAB进行分析。

传统的实验方法是在齿轮箱体上安装加速度传感器(图8(a))，本文在从动轮体上接近裂纹的位置对称地安装了两个加速度传感器(图8(b))，这样就大大地缩短了振动信号的传递路径。传感器选用型号：箱体上使用四个单向压电式加速度传感器(IEPE)，型号是CA-YD-186；在从动轮上加工了两个孔，用来固定YD77SA 三向加速度计。

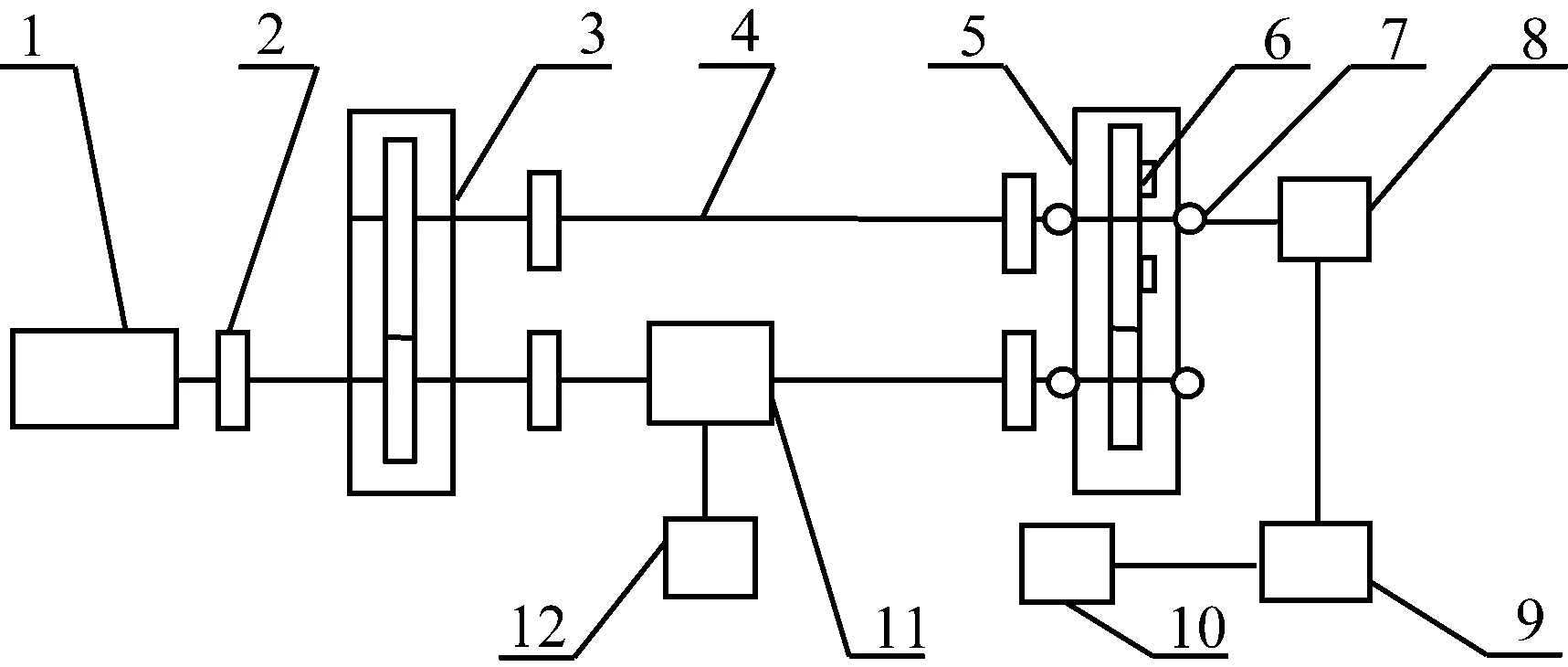
1-电机；2-联轴器；3-陪试齿轮箱；4-扭力杆；5-实验齿轮箱；6-传感器；7-加速度传感器；8-集流环；9-信号采集系统；10-计算机；11-扭矩转速传感器；12-扭矩测量仪

图7 齿轮传动实验台原理图
Fig.7 Schematic of the gearbox setup

(a)箱体上(b)轮体上

图8 传感器的安装

Fig.8 The locations of sensors

齿轮体上传感器信号通过安装在轴端的的集流环传递给信号采集系统。在从动轮的齿根处，人工加工长度为2 mm的裂纹，并且裂纹贯穿轮齿(图9)，实验的齿轮参数与仿真一致，实验时转速取大约为300 r/min，600 r/min、900 r/min及1 200 r/min，所加的扭矩分别为100 Nm、200 Nm、300 Nm及400 Nm。本文取的是当负载为400 Nm，转速为1 206 r/min时的振动信号进行分析。根据齿轮系统的参数和采样定理,采样频率为8 kHz，此时主动轮的转频为20 Hz，从动轮的转频为13.33 Hz，轮齿的啮合频率为600 Hz。通过齿轮传动系统试验来验证新的测试方法的有效性，由于试验的局限性，本文只对裂纹故障状态在不同转速和力矩情况下进行了验证。

图9 齿根裂纹Fig.9 Gear tooth root crack

3.2 实验结果分析

由于噪声的干扰，对实验信号进行了降噪处理[15]，图10和图11是实测信号的时域图，与仿真结果基本一致，箱体上的振动信号没有反映出齿轮的裂纹故障特征，齿轮体上的振动信号反映了齿轮裂纹的故障特征，并且脉冲的频率f=1/Δt=13.33 Hz为裂纹齿轮所在轴的转频。

(a) 箱体信号

(b) 轮体信号图10 健康齿轮传动系统振动信号时域图Fig.10 The time-domain signalsof healthy gear system

(a) 箱体信号

(b) 轮体信号图11 故障齿轮传动系统振动信号时域图Fig.11 The time-domain signalsof fault gear system

裂纹是齿轮箱多种故障中比较难识别的故障[16]，当齿轮出现裂纹时，振动信号的调幅效应和调频效应同时存在，因此频谱上的调制边频带不再对称。为了进一步分析故障特征，对时域信号进行循环自相关分析。根据解调原理，调幅调频效应同时存在会导致信号的循环域低频段出现调制源的一倍频或二倍频及以上成分，高频段出现以啮合频率为中心频率，以故障齿轮所在轴的转频为调频的边频带[17]。频域分析结果如图12和图13。可以看出，无论是健康齿轮还是故障齿轮，频率成分都有啮合频率的二倍频及其边频带。低频处有两个主要频率成分：13.33 Hz和20 Hz，它们主要是由于传动系统的装配误差，啮合刚度的变化等造成的。高频处是以啮合频率的二倍频为中心，以13 Hz和20 Hz为调频的边频带。对比箱体传感器上的信号，如图12的(a)与(b)，可以发现，无论在高频段还是低频段，出现的频率成分的大小和幅值几乎一样，无法诊断出哪个齿轮出现故障。对比来自齿轮体传感器上的振动信号，如图13(a)与(b)所示，可以看出，13(b)中低频段不仅出现了冲击频率13.2 Hz的一倍频、二倍频及三倍频，而且与图13(a)相比，13.2 Hz振幅也增大许多，在高频段，出现了以啮合频率的二倍频为中心，以调频及其倍频(f2，2f2，3f2)为间隔的边频带，而f2是故障齿轮所在轴的转频。根据解调原理，这些频率成分都是由齿根裂纹故障引起。因此从齿轮体上的振动信号中能诊断出从动轮为故障齿轮。

(a) 健康齿轮系统

(b) 2 mm裂纹故障齿轮系统图12 箱体上传感器的振动信号Fig.12 The frequency-domain signalson gearbox

(a) 健康齿轮系统

(b) 2 mm裂纹故障齿轮系统图13 嵌入式传感器的振动信号Fig.13 The frequency-domain signalson gear body

4 结 论

目前，齿轮箱的振动信号都是通过安装在齿轮箱体上的传感器得到，由于齿轮故障引起的振动信号通过齿轮体、齿轮轴、轴承及轴承座等复杂的传递路径后，幅值会衰减，有的频率成分会丢失。本文提出的嵌入式传感器测试方法，缩短了振动信号的传递路径，降低信号在传递过程中的衰减，提高了信号的信噪比通过对齿根2 mm裂纹的齿轮传动系统进行显式动力学分析和实验验证，得出了一致的结论：嵌入式传感器上的振动信号能有效地诊断出了齿轮传动系统的早期裂纹故障，而箱体上的传感器的振动信号则无法诊断出裂纹故障。这为齿轮传动系统早期的故障提供了一种新的测试方法。

参 考 文 献

[1] 王洪明，郝旺身，韩捷，等.基于LMD和样本熵的齿轮故障特征提取方法研究[J].郑州大学学报(工学版),2015,36(3):44-48.

WANG Hongming,HAO Wangshen,HAN Jie, et al. Research on gear fault feature extraction based on LMD and sample entropy[J].Journal of Zhengzhou University(Engineering Science),2015,36(3):44-48.

[2] 侯高雁,吕勇,肖涵，等.基于LMD 的多尺度形态学在齿轮故障诊断中的应用[J].振动与冲击,2014,33(19):69-73.

HOU Gaoyan, LÜ Yong, XIAO Han,et al.Application of multi-scale morphology based on LMD in gear fault diagnosis[J].Journal of Vibration and Shock,2014,33(19):69-73.

[3] 王志坚，韩振南，刘邱祖，等.基于MED-EEMD的滚动轴承微弱故障特征提取[J].农业工程学报,2014,30(23):70-78.

WANG Zhijian, HAN Zhennan, LIU Qiuzu, et al. Weak fault diagnosis for rolling element bearing based on MED-EEMD[J].Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(23): 70-78.

[4] CHEN Xihui, CHENG Gang, SHAN Xianlei. Research of weak fault feature information extraction of planetary gear based on ensemble empirical mode decomposition and adaptive stochastic resonance[J]. Measurement,2015,73(8):55-67.

[5] JIANG Hongkai, LI Chengliang, LI Huaxing. An improved EEMD with multi-wavelet packet for rotating machinery multi-fault diagnosis[J]. Mechanical Systems and Signal Processing,2013,36(2):225-239.

[6] LEAH M K,RUSSEL R. Embedded diagnostics and prognostics synchronizationfor army transformation[C]//Proceedings of IEEE Aerospace Conference.[S.l.]:IEEE,2004.

[7] 陈仲生,杨拥民,李聪,等,基于振动传递符号有向图的齿轮箱嵌入式传感器优化配置模型与算法[J].航空动力学报,2009,24(10)：384-2490.

CHEN Zhongsheng, YANG Yongmin, LI Cong, et al. Model and algorithm of optimal embedded sensors placement for gearboxes based on signed directed graph of vibration propagation[J].Journal of Aerospace Power, 2009, 24(10):2384-2490.

[8] SMITH W, DESHPANDE L, RANDALL R, et al. Gear bearing diagnostics in a planetary gearbox: a study using internal and external vibration signals[J]. International Journal of Condition Monitoring,2013,3(2):36-41.

[9] FAN Zhiqi, LI Huaizhong.A hybrid approach for fault diagnosis of planetary bearings using an internal vibration sensor[J].Measurement,2015,64(8):71-80.

[10] 张刚，何永慧，张义民.滚动轴承的多体接触动力学仿真[J].振动、测试与诊断,2013,33(增刊1)：28-33.

ZHANG Gang, HE Yonghui, ZHANG Yimin. Multi-body contact dynamics simulation of rolling bearing[J].Journal of Vibration, Measurement & Diagnosis, 2013,33(Sup1)：28-33.

[11] 陈小安，缪莹，杨为，等.基于有限单元法的多间隙耦合齿轮传动系统非线性动态特性分析[J].振动与冲击,2010,29(2):46-52.

CHEN Xiao’an, MIAO Ying, YANG Wei, et al. Nonlinear dynamic characteristics analysis of a geartransmissionsystem with multiple clearances based on finite elementmethod[J]. Journal of Vibration and Shock, 2010,29(2):46-52.

[12] 赵海鸥.LS-DYNA动力分析指南[M].北京:兵器工业出版社,2003.

[13] 李尧臣, 王自强. 在裂纹尖端引入位移协调奇异单元的有限单元法[J].力学季刊, 1983(3):82-102.

LI Yaochen, WANG Ziqiang. The finite element method by using the singular element with concordant displacement at the crack tip[J]. Chinese Quarterly of Mechanics, 1983(3):82-102.

[14] 李晓贞, 朱如鹏, 李政民卿,等. 齿面摩擦对面齿轮传动系统振动特性的影响分析[J]. 振动工程学报, 2014, 27(4):583-588.

LI Xiaozhen, ZHU Rupeng, LI Zhengminqing, et al. Influences of frictional coefficient on vibration characteristic of face-gear transmission system[J]. Journal of Vibration Engineering, 2014, 27(4):583-588.

[15] NING Shaohui, HAN Zhennan, WANG Zhijian. Application of sample entropy based LMD-TFPF de-noising algorithm for the gear transmission system[J]. Entropy,2016,18(11):414.

[16] 丁康,李巍华.齿轮及齿轮箱故障诊断实用技术[M].北京:机械工业出版社,2005：63-65.

[17] 李力, 廖湘辉. 应用循环自相关函数诊断齿轮故障[J]. 三峡大学学报(自然科学版), 2003, 25(2):129-133.

LI Li, LIAO Xianghui. Applying cyclic autocorrelation function to diagnose gear faults[J]. Journal of China Three Gorges University(Natural Sciences), 2003, 25(2):129-133.