基于频响函数法的固定结合部参数辨识研究

田丰庆， 朱坚民， 李孝茹， 李 尧(上海理工大学 机械工程学院，上海 200093)

机械结构中存在着大量的固定连接，如栓接、铆接、焊接、粘接等，固定结合部的存在增加了整体结构的阻尼，减小了整体结构的刚度，使整体结构的动态特性变差。因此准确地辨识结合部参数对确定整体结构的动态特性具有重要意义。

固定结合部等效参数的辨识方法主要有模态分析法与频响函数法[1]。模态分析法的基本思想是将机械结构的动力学方程变换到模态坐标空间，并截去部分高阶模态后确定结合部的数学模型[2]。该方法的特点是需要准确确定整体结构的模态参数，对于整体结构模态相对密集的对象难以应用。频响函数法的基本思想是根据机械结构中子结构之间的连接关系，耦合各子结构的频响函数确定整体结构的频响函数，再对结合部参数进行辨识。频响函数法原理简单、实验方便、应用广泛。

针对上述问题，本文以螺栓连接的两个金属梁的栓接结合部为例进行研究，采用频响函数法建立其动力学模型，提出对结合部中各参数项单独灵敏度分析、单独辨识的方法。通过仿真与实验算例验证该方法的正确性。

1 基本原理

1.1 频响函数法辨识固定结合部参数的基本原理

机械结构通常可以拆分为子结构与连接子结构的结合部，如图1所示，整体结构W拆分为子结构A、B和结合部J。其中e1、e2表示结合部部分，a、b表示结合部以外部分。根据子结构A、子结构B以及整体结构W频响函数的定义，可得位移与外力的关系式，如式(1)～(3)所示。式中X表示结构的位移矢量，F表示结构的力矢量，H表示频响函数。下标A、B表示对应的子结构，W表示整体结构。下标a、b、e1、e2表示频响函数对应的激励点、响应点，如Hae1表示在e1点激励 a点响应的频响函数。上标有*代表此项参数为整体结构的参数，上标无*代表此项参数为子结构的参数。

图1 子结构与整体结构关系示意图Fig.1 Relationship between substructure and assembly structure

(1)

(2)

(3)

假设结合部不受外力，则结合部之间的力为作用力与反作用力，如式(4)所示。由于结合部的频响函数HJ与等效阻抗ZJ互逆，可得式(5)。忽略结合部的质量，结合部的动力学公式可以表示为式(6)

Fe1=-Fe2

(4)

(5)

Xe2-Xe1=HJFe1

(6)

联合式(1)～(6)，可得整体结构的原点、跨点频响函数如式(7)～(10)所示

(7)

(8)

(9)

(10)

由式(7)～(10)可以推导出相应的4个结合部参数的辨识公式，如式(11)～式(14)。这4个辨识公式分为两组，式(11)与式(14)为第一组，式(12)与式(13)为第二组。第一组的两个公式都采用整体结构的原点频响函数作参数，只是对应整体结构的原点不同。因此将第一组的两个公式等效为一个辨识公式如式(11)。第二组与第一组情况相似，不同的是第二组公式采用了整体结构的跨点频响函数，可将第二组公式等效为式(12)所示的辨识公式

(11)

(12)

(13)

(14)

根据上述公式辨识结合部参数需要先求取公式中的频响函数。以式(11)中的频响函数He1a为例说明，如果a、e1两节点都只有一个自由度，则He1a意义明确，代表一个频响函数。如果a、e1两节点都有两个自由度，如欧拉梁模型，则He1a代表4个频响函数组成的频响函数矩阵。分别为平移振动的频响函数(平动频响函数)、扭转振动的频响函数(转动频响函数)、平移与扭转振动耦合的频响函数(耦合频响函数)。

对子结构而言，根据有限元理论建立子结构的有限元模型，可以计算其所有频响函数(包括平动、转动及耦合频响函数)。对整体结构而言，由于结合部参数未知，无法构建整体结构的有限元模型，需用实验方法得到所有频响函数。其中平动频响函数可以通过实验测得，但转动与耦合频响函数需专门的测量设备[17]。本文采用有限差分法[18]通过两点分别激励，并测量其响应的平动频响函数后再计算出其中一点的所有频响函数。

1.2 有限差分法计算转动频响函数

以梁结构为模型说明转动频响函数的求法，计算如图2中B点激励B点响应的所有频响函数。在B点附近设置A点，分别激励A点、B点，并且在A点、B点测试响应信号，可得平动频响函数HAA_tt、HAB_tt、HBA_tt、HBB_tt，组成矩阵如式(15)，其中字母tt表示平动频响函数。

设A、B两点之间的距离为s，确定前向差分公式如式(16)所示。由式(17)可以计算出B点激励B点响应的所有频响函数。字母rr表示转动频响函数，字母tr、rt表示耦合频响函数。

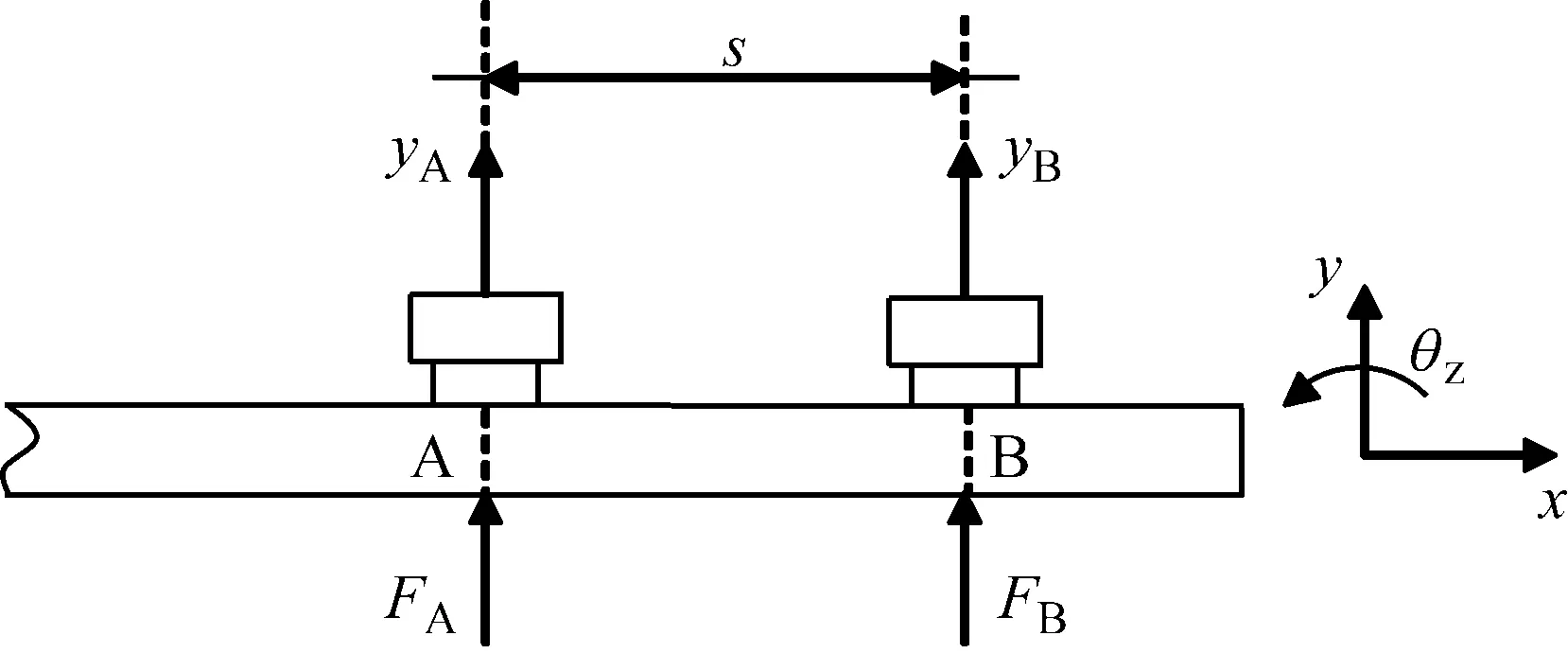
图2 有限差分法求B点频响函数Fig.2 Finite difference method for FRFs of point B

(15)

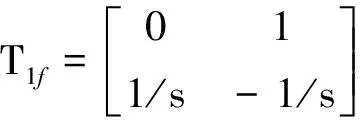
(16)

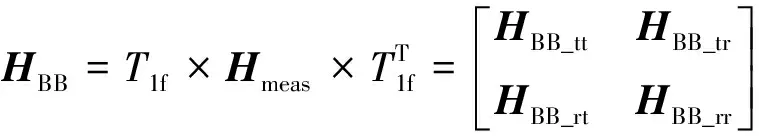
(17)

1.3 结合部参数单独辨识原理

由辨识公式(11)、(12)可知，如果辨识公式中子结构和整体结构的频响函数可以确定，则结合部的参数可以通过两个辨识公式中任意一个计算得到。从理论上讲，对应于每个频率都可计算出一组结合部参数，并且计算结果应该相等。但事实并非如此，计算的结果不相同甚至部分结果相差较大。如何找出相对误差较小的结合部参数所对应的辨识频段是准确辨识结合部参数的关键。

本文方法的主要思路是：通过仅改变结合部参数中某一项参数的大小得到几组新参数，如以2倍、1倍与0.5倍参数为例的三组参数。用该三组参数模拟结合部对整体结构进行模态分析，对比三组参数分析得出的固有频率值，得到该参数由0.5倍变至2倍时引起的每一阶固有频率的相对变化量，用相对误差表示，相对误差越大，表示该参数对此阶固有频率值的影响越大，则该参数在此阶固有频率处的灵敏度越高。根据李玲等的研究，在灵敏度高的频段可以准确地辨识出结合部参数。本文采用上述方法确定某一结合部参数的灵敏模态，并在该模态处辨识参数，并依此方法辨识出所有的结合部参数。

2 仿真算例研究

2.1 集中质量模型

集中质量法在机械结构结合部参数建模中应用广泛，在集中质量模型中结合部多数采用线性弹簧阻尼单元模拟。本文首先以集中质量模型为例进行研究，构建集中质量模型如图3所示，整体结构W拆分为子结构A、子结构B及结合部J。结合部采用一组弹簧阻尼单元模拟，用ZJ表示结合部等效阻抗，kJ和cJ分别表示结合部的刚度和阻尼，建立其等效模型,如式(18)所示。

Model 1ZJ=kJ+iwcJ

(18)

图3 集中质量模型Fig.3 Lumped mass model

集中质量模型中的参数如表1所示。利用有限元理论可计算子结构A、B的频响函数。

构建整体结构的有限元模型，可求得整体结构前4阶的固有频率分别为228 Hz、449 Hz、781 Hz、853 Hz。

根据1.3节的分析，用3组kJ的不同倍数的结合部参数kJ+iwcJ、2×kJ+iwcJ及0.5×kJ+iwcJ分别模拟结合部并进行模态分析，将计算出的3条频响函数曲线绘制在图5中，同时将对应的整体结构固有频率值列于表2。对每一阶模态，用0.5kJ与2kJ作为结合部参数对应的固有频率的差值除以kJ作为结合部参数对应的固有频率值，得此kJ由0.5倍～2倍的变化量下所引起的这一阶固有频率值的变化率，用相对误差表示，见表2。

表1 集中质量模型参数表Tab.1 Parameters of the lumped mass model

图4 频响函数的理论值与噪声值Fig.4 Theoretical and noisy value of

表2 kJ灵敏度分析表Tab.2 Sensitivity analysis of kJ

图5 对kJ灵敏度分析Fig.5 Sensitivity analysis of kJ

由表2和图5可知，刚度kJ在整体结构前4阶模态处的灵敏度不相同。在第1阶、第3阶模态处，不同倍数的kJ对应的固有频率值变化较小，在这两阶模态处不灵敏。在第2阶、第4阶模态处，从图5看出固有频率值有较大变化，由相对误差的数值分析可知，kJ的大小变化在第2阶模态引起的误差最大，达到10.2%，因此刚度kJ在整体结构的第2阶模态处灵敏度最高。则本算例中刚度kJ在第2阶固有频率(449 Hz)处辨识。

图6为根据式(11)辨识的kJ值，由图6可知在每个频率处所计算出的结合部参数值并不相等，有些与理论值之间还有较大的误差，但在参数kJ最灵敏的模态频率(449 Hz)附近，计算值与理论值比较接近。图7表示的是结合部阻尼参数cJ的辨识情况，其辨识方法与刚度参数的辨识方法相同。

采用式(12)辨识参数的方法与式(11)的辨识方法相同，两者的辨识结果列于表3。

图6 式(11)的计算出的kJ值Fig.6 The values of kJ calculated by formula (11)

图7 式(11)计算出的cJ值Fig.7 The values of cJ calculated by formula (11)

由表3可知，式(11)和式(12)的辨识结果差异较小,式(11)的辨识精度略高。这主要是由于辨识公式(11)中采用整体结构的原点频响函数作为参数，辨识公式(12)中采用整体结构的跨点频响函数作为参数。对比这两种频响函数，原点频响函数的精度比跨点频响函数略高，这与文献[14]的结论一致。

表3 集中质量模型结合部参数辨识结果Tabl.3 Parameter identification result of thejoint in lumped mass model

当结合部等效为单自由度弹簧阻尼单元时，式(11)和式(12)的辨识结果差异较小，具体应用时可根据实际情况中容易获得的频响函数选择合适的辨识公式。

2.2 欧拉梁模型

如图8所示的两个子结构是两端自由的欧拉梁，e1与e2固定连接组成整体结构。结合部采用2节点4自由度的刚度矩阵模拟,建立结合部的等效模型如式(19)所示。式中ZJ表示结合部等效阻抗，ktt表示平动刚度，krr表示转动刚度，ktr和krt示耦合刚度，c表示对应的阻尼，w表示角频率。则辨识公式(11)、(12)中的频响函数为平动、转动、耦合频响函数组成的矩阵。

(19)

图8 欧拉梁模型Fig.8 Euler-Bernoulli beam model

梁的弹性模量为1.97×1011Pa，密度为7 865 kg/m3，根据有限元理论可计算出子结构A、B的所有频响函数。

基于表4中的结合部参数，建立整体结构的有限元模型，其中耦合参数ktr和krt相等，ctr和crt相等。可得整体结构在0～1 000 Hz以内有四阶固有频率，分别为87 Hz、249 Hz、466 Hz、794 Hz。采用前述灵敏度分析方法，对结合部参数ktt、krt(ktr)和krr分别进行灵敏度分析，分析结果如图9～11所示。

由图9可知，平动刚度ktt在整体结构第1、2、3阶模态处不灵敏，在第4阶模态处最灵敏；由图11可知，转动刚度krr在整体结构第1、2、4阶模态处不灵敏，在第3阶模态处最灵敏；由图10可知耦合刚度ktr在所考虑的频段都不灵敏。

图9 对ktt的灵敏度分析Fig.9 Sensitivity analysis of ktt

图10 对ktr的灵敏度分析Fig.10 Sensitivity analysis of ktr

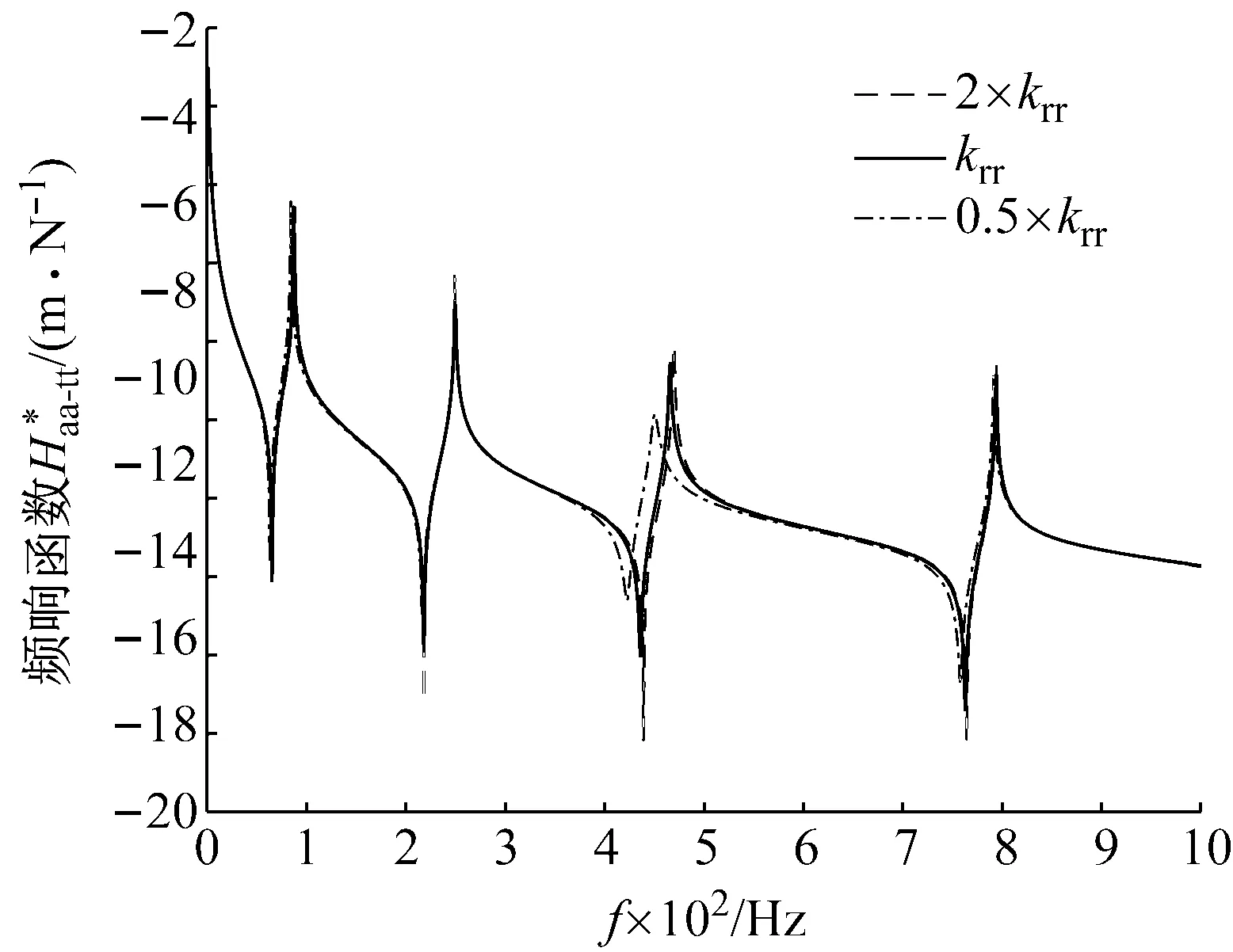
图11 对krr的灵敏度分析Fig.11 Sensitivity analysis of krr

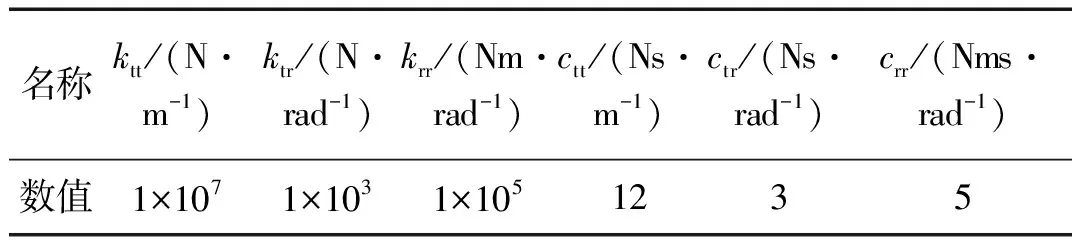
表4 结合部参数表Tab.4 Parameters of the joint

图12 式(11)计算出的ktt值Fig.12 ktt calculated by formula (11)

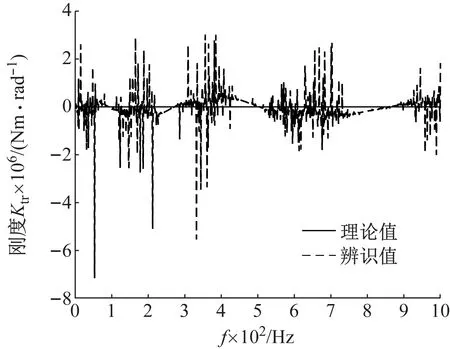
图13 式(11)计算出的ktr值Fig.13 ktr calculated by formula (11)

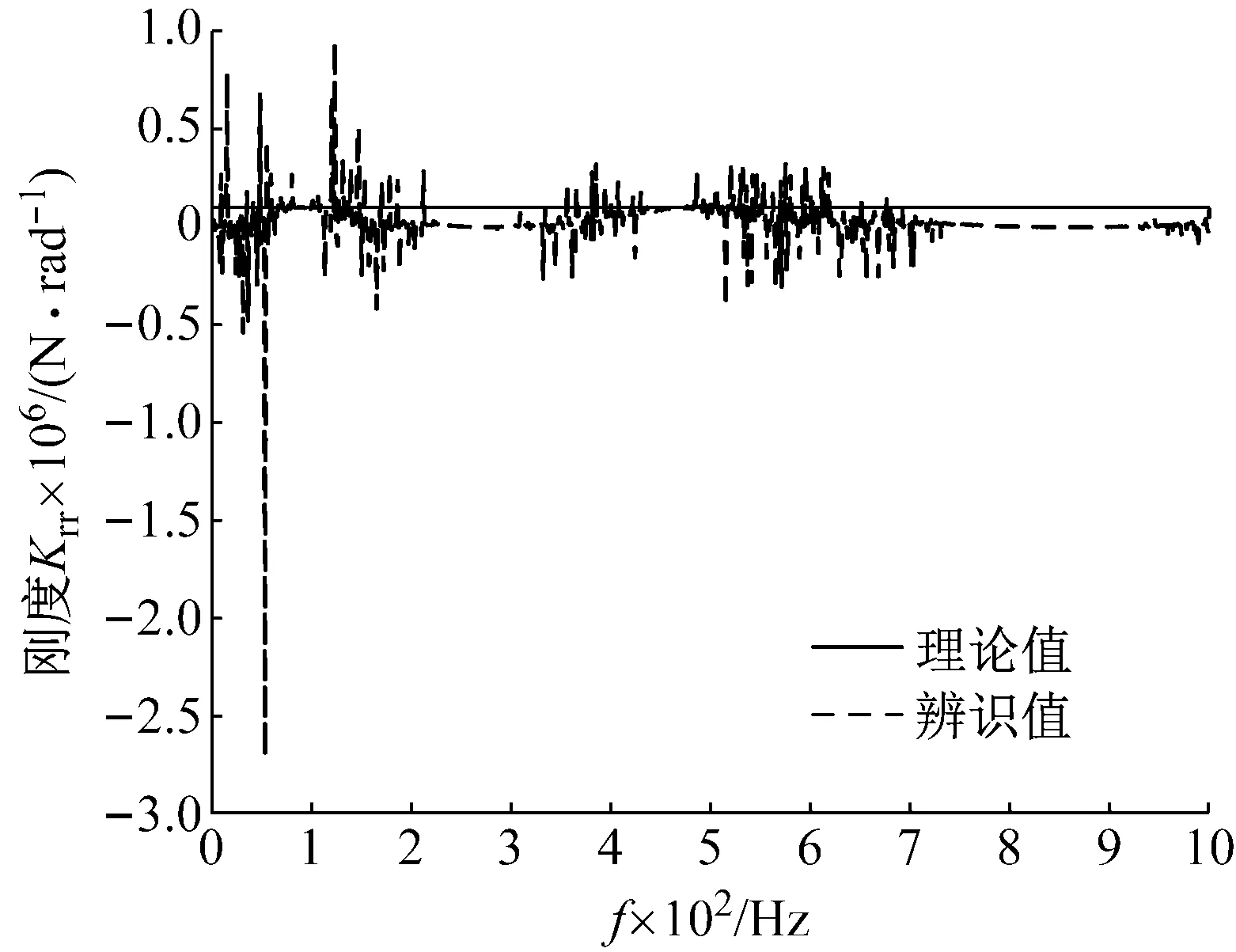
图14 式(11)计算出的krr值Fig.14 krr calculated by formula (11)

由表5可知，与集中质量模型的算例结果类似，采用式(11)辨识结果的误差比式(12)的误差小。

耦合参数在整体结构的所考虑的频段都不灵敏，即耦合参数的大小变化对整体结构的动态特性影响较小，具体辨识过程中很难准确辨识。表5中耦合参数的误差较大也印证了这一点。对于此类情况，可忽略结合部的耦合参数，直接构建结合部等效模型如式(20)所示

表5 辨识公式的结果Tab.5 Parameter identification result

(20)

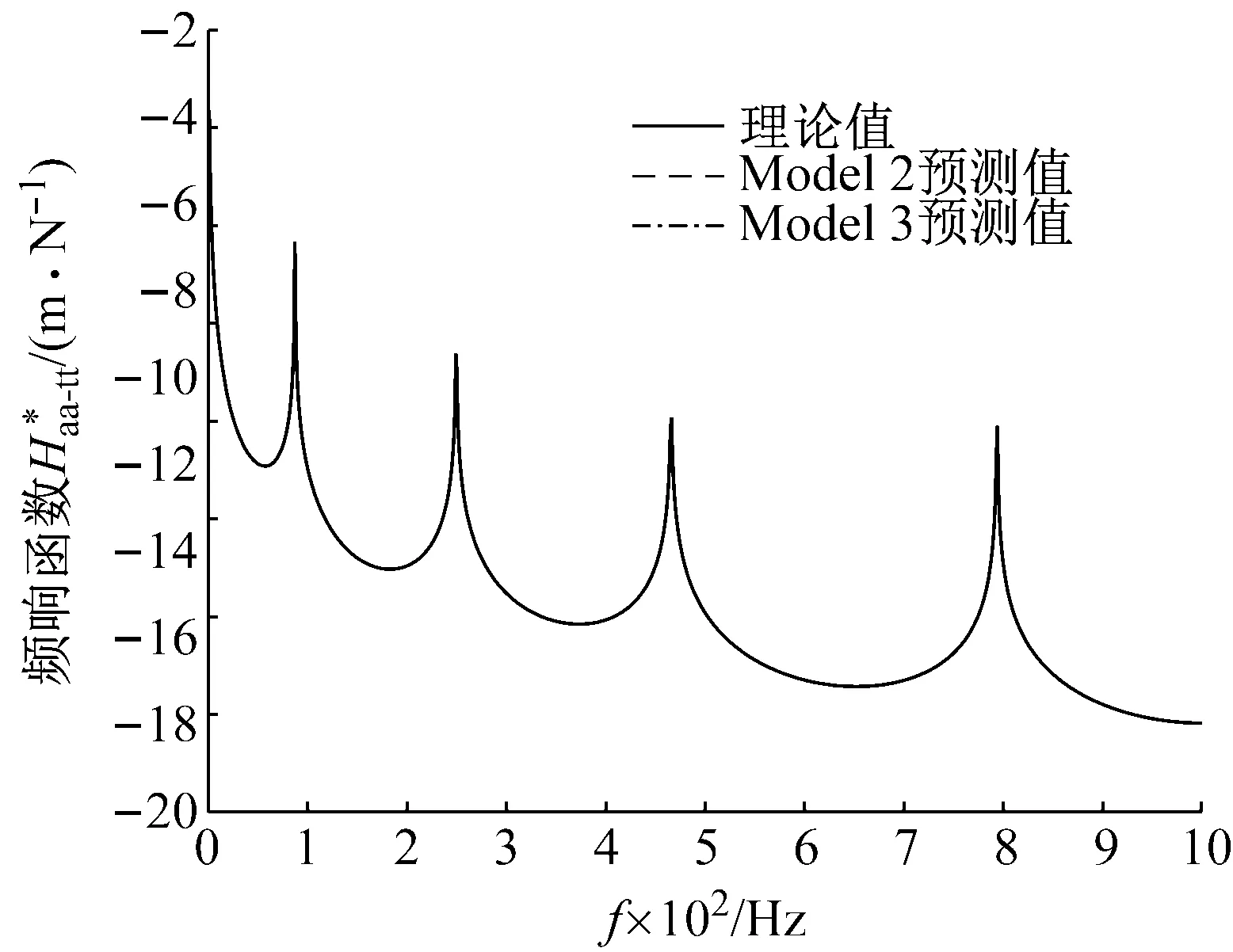
图15 整体结构频响函数的预测值与理论值对比图Fig.15 Comparison between the predicted values and the theoretical values of assembly structure FRFs

3 实验算例研究

图17为实验时测试点分布的具体位置及子结构单元划分图。两个子结构的材料为Q235，通过e1、e2点连接。子结构A的长度为400 mm，子结构B的长度300 mm，梁结构的截面宽为30 mm、高为10 mm，a、b、e1、e2为具体的激励点与响应点。

采用Model 3模拟整体结构的结合部，选取辨识式(11)辨识结合部参数。

图16 实验原理Fig.16 Experimental principle

图17 实验测试点分布图Fig.17 Testing location distribution

3.1 计算子结构频响函数

实验材料的密度为7 803 kg/m3，弹性模量为1.95×1011Pa。建立子结构A和子结构B的有限元模型，子结构A划分为15个单元，子结构B划分为14个单元，计算出辨识公式(11)中子结构A与子结构B的所有频响函数。

3.2 计算整体结构a点的频响函数

在a点附近设置c点，a点距离子结构A的端部为30 mm，a、c两点之间的距离为s=30 mm。

分别激励a点、c点，读取a点、c点的响应，得相应的平动频响函数曲线，如图18所示。由式(17)计算得整体结构a点激励a点响应的所有频响函数，表示在图19中。同时可得在0～1 000 Hz以内整体结构有4阶固有频率，分别为92 Hz、300 Hz、564 Hz、900 Hz。

图18 实验测试a点、c点的频响函数Fig.18 Experimental FRFs result of location a and c

图19 整体结构a点的频响函数Fig.19 FRFs result of point a to assembly structure

3.3 灵敏度分析

电化学问题离不开电子的行为，说它是电化学理论的灵魂并不过分，电子的行为表现为定向和定量两个方面。定向方面列表如下：而定量方面可对原电池及电解池的相关问题进行全面的计算。

表6 遗传算法寻优结果Tab.6 Optimization result of GA

3.4 结合部参数的辨识

图20 对ktt灵敏度分析Fig.20 Sensitivity analysis of ktt

图21 对krr灵敏度分析Fig.21 Sensitivity analysis of krr

表7 ktt灵敏度分析表Tab.7 Sensitivity analysis of ktt

图22 整体结构的频响函数Fig.22 FRFs of assembly structure

表10 遗传算法与本文方法的辨识结果对比Tab.10 Identification result comparison betweenGA and the proposed method

4 结 论

(1)提出一种对结合部参数辨识的新方法。先通过遗传算法寻优确定结合部参数的初值，再对结合部各项参数进行单独灵敏度分析，计算该参数在每一阶模态处的灵敏度，在最灵敏的模态处单独辨识该项参数，最后依此方法辨识所有的结合部参数。

(2)仿真和实验算例的研究结果表明，基于本文方法辨识的结合部参数所预测的整体结构频响函数与实验测试的频响函数具有较高的一致性，从两者的固有频率的对比结果看，最大的相对误差出现在第1阶，为1.09%，参数辨识精度较高。

参 考 文 献

[1] 蔡力钢,王锋,李玲，等.栓接结合部动态特性研究进展[J].机械工程学报,2013,49(9):158-168.

CAI Ligang, WANG Feng, LI Ling, et al. Review on dynamic properties of bolted joints[J]. Journal of Mechanical Engineering, 2013, 49(9):158-168.

[2] 李金峰,王立平.改进的受力状态映射法在结合部动力学参数辨识中应用[J].振动与冲击,2016,35(6):488-496.

LI Jinfeng,WANG Liping. Application of an improved force-state mapping method in dynamic parameter identification of joints[J]. Journal of Vibration and Shock, 2016, 35(6):488-496.

[3] OKUBO N, MIYAZAKI M. Development of uncoupling technique and its application[C]//Proceedings of International Modal Analysis Conference. Orlando, FL，1984.

[4] TSAI J S, CHOU Y F. The identification of dynamic characteristics of a single bolt joint[J]. Journal of Sound and Vibration, 1988, 125:487-502.

[5] WANG J H, LIOU C M. Experimental substructure synthesis with special consideration of joint effect[J]. International Journal of Analytical and Experimental Modal Analysis, 1989, 5(1):1-12.

[6] HWANG H Y. Identification techniques of structure connection parameters using frequency response functions[J]. Journal of Sound and Vibration, 1998, 212(3):469-479.

[9] REN Y, BEARDS C. F. Identification of joint properties of a structure using FRF data[J]. Journal of Sound and Vibration, 1995, 186(4):567-587.

[10] YANG T, FAN S H, LIN C S. Joint stiffness identification using FRF measurements[J]. Computers & Structures, 2003, 81: 2549-2556.

[11] MEHRPOUYA M, SANATI M, PARK S S. Identification of joint dynamics in 3D structures through the inverse receptance coupling method[J]. International Journal of Mechanical Sciences, 2016, 105: 135-145.

[12] 李玲,蔡安江,蔡力钢，等.栓接结合部动态特性辨识方法[J].机械工程学报,2013,49(7):168-175.

LI Ling, CAI Anjiang, CAI Ligang, et al. Identification method for dynamic properties of bolted joints[J]. Journal of Mechanical Engineering, 2013, 49(7):168-175.

[13] 李玲,蔡力钢,郭铁能，等.机械结合部动态刚度辨识与实验研究[J].振动工程学报,2012,25(5):488-496.

LI Ling, CAI Ligang, GUO Tieneng, et al. Identification and experimental research on dynamic stiffness of mechanical joints[J]. Journal of Vibration Engineering, 2012, 25(5):488-496.

[14] 郭铁能,李玲,蔡力钢，等.基于频响函数辨识机械结合部动态参数的研究[J].振动与冲击,2011,30(5):69-72．

GUO Tieneng, LI Ling, CAI Ligang, et a1. Identifying mechanical joint dynamic parameters based on measured frequency response functions[J]. Journal of Vibration and Shock, 201l, 30(5):69-72．

[15] 李玲,蔡安江,蔡力钢，等.栓接结合部动态特性参数辨识新方法[J].振动与冲击,2014,33(14):15-32.

LI Ling, CAI Anjiang, CAI Ligang, et al. New method to identify dynamic characteristics of bolted joints[J]. Journal of Vibration and Shock, 2014, 33(14):15-32.

[16] 董冠华,殷勤,殷国富，等.机床结合部动力学建模与辨识方法的研究[J].机械工程学报,2016,52(5):162-168.

DONG Guanhua, YIN Qin, YIN Guofu, et al. Research on dynamics modeling and identification of machine tool joints[J]. Journal of Mechanical Engineering, 2016, 52(5): 162-168.

[17] KLERK D, RIXEN D, VOORMEEREN S, et al. Solving the RDOF problem in experimental dynamic substructuring[C]//Proceedings of the 26th international Modal Analysis Conference. Orlando, FL, 2008.

[18] DUARTE M L M,EWINS D J. Rotational degrees of freedom for structural coupling analysis via finite difference technique with residual compensation[J]. Mechanical Systems and Signal Processing, 2000, 14(2):205-227.