与荷载同步变化的时间步自动调整方法

李 彬, 唐小微(大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

随着科技的不断进步，计算机硬件的高速发展非常有效地提高了计算效率，但是不论硬件如何提高，通过对计算方法的改进与对新计算方法的开发来提高计算效率，依然是一件非常重要和有意义的事情。

提高计算效率的方法有很多种，众多学者在这方面的努力一直没有停止过。例如，王林等[1]研究基于改进MP的稀疏表示快速算法，该算法能准确提取滚动轴承故障特征且提高了计算效率；为减少谐波合成法中功率谱矩阵分解的计算量, 祝志文等[2]提出了谱解矩阵双轴插值算法和递归插值算法，两种方法均使风场模拟计算效率大幅度提高；张斌等[3]提出一种将有限元法和非线性接触理论相结合的交叉迭代数值改进算法，极大地提高了动力学方程数值计算效率。张弛等[4]提出一种改进的混合免疫算法，提高了种群多样性和收敛性,减少了时间复杂度,提高了计算效率。

在众多方法中，时间自适应分析方法受到越来越多的关注。它将误差控制在某一允许范围内，同时尽可能地减少计算时间，这样就在保证计算精度的同时节省了计算时间，最终提高了计算效率。在时间自适应研究领域方面，许多国内外学者做出了努力。在岩土工程固结分析中，Sloan等[5]应用了时间自适应算法。Zienkiewicz等[6]提出了一种简单的时间自适应方法，并成功应用到动力分析中。Zeng等[7-8]对Zienkiewicz提出的方法进行了改进。Tang等[9]通过控制全局误差，将时间自适应方法应用到地下水流动分析中。Kavetski等[10]采用了启发式和误差评估的方法进行了时间自适应。Kuo等[11]结合时间元素具有大时间步幅及动量平衡具对不连续载重的平滑化的优点，提出了一套加权式动量时间元素的逐步时间积分方法。王开加等[12]在海上浮基风电平台绕流数值模拟分析中，采用了时间自适应技术。毛卫男等[13]提出了一种适应时间的方法，并应用于土壤冻结的水热耦合模型中。Tang等[14-15]开发了一套完整的时间自适应方法，并在地震液化模拟中进行了应用。Naveed等[16]将高阶变分离散时间的自适应时间控制应用到了对流-扩散反应方程中。Vahid等[17]应用时间适应方法，在裂纹扩展的相场公式中进行了大规模的并行处理。Marc等[18]对非线性和时间相关的误差估计和自适应问题作了一个简单的概括，并指出了目前的时间自适应方法为后验式方法。

在结构动力时程分析中，本文针对由时间步长引起的误差，建立了相对误差与时间步长之间的关系式。并将设定的目标误差限代入此关系式中，反算出时间步长。这样，得到的每一步时间步长所对应的相对误差与给定目标误差限相等，由此保证了计算精度。同时，极大的节省计算时间，有效的提高了计算效率。

1 自适应原理与自适应时间步长确定方法

1.1 原理

时间步长固定的时间离散动力分析方法中，一般来说，时间步长越小，所产生的误差越小，计算精度越高。固定的时间步长在计算过程中产生的误差有大有小，而一个算法所能达到的计算精度是由计算结果最差情况，也就是产生的最大误差所决定的。当取某一固定时间步长进行计算时，每一时间步所产生的误差不一定相同，误差中较小部分对应的固定时间步长无疑占用了较多的时间资源，浪费了时间。本文研究的方法出发点就是通过增加误差中较小部分对应的时间步长，使得增加后的时间步长所产生的误差刚好达到所有固定步长产生误差中的最大误差，这样，就能在保证计算精度的同时，大大的节省计算时间。

在计算过程中，先设定某一相对误差限，这个相对误差限就对应于所有固定步长产生误差中的那个最大误差。理论上，由该相对误差限计算得到的每一个时间步长所对应的相对误差是一致的(与设定的相对误差限相等)，这也使得计算精度得到了保证。如果时间步长再增加一点点，所对应的相对误差都会超过相对误差限。所以，计算得到的每一个时间步长已经达到最大。理论上，该方法在保证计算精度的同时，最大化地节省了计算时间，提高了计算效率。

1.2 自适应时间步长的确定

结构动力数值分析方法中，动力控制微分方程通常具有如下形式

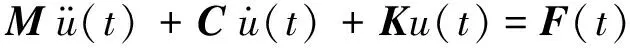
(1)

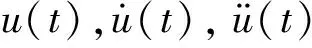
由Newmark-β法，上述动力微分方程tn+1时刻位移近似解ui+1(t)可以表达为

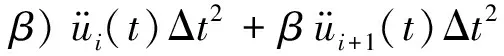
(2)

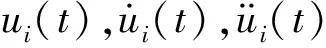
(3)

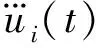
将式(3)代入(2)得

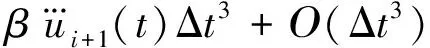
(4)

Ο(Δt3)=

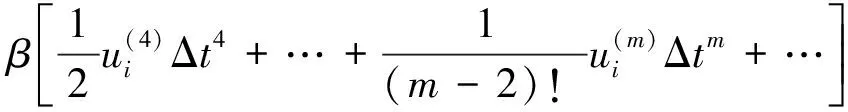
(5)

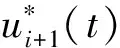
(6)

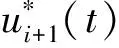
(7)

计算相对误差时需要精确解，然而精确解通常是难以获得的，这里采用泰勒级数的展开法获得ti+1时刻位移的解来替代精确解进行误差评估，其表达式为

(8)

(9)

将式(4)、(5)、(8)和(9)代入式(7)中，整理后得

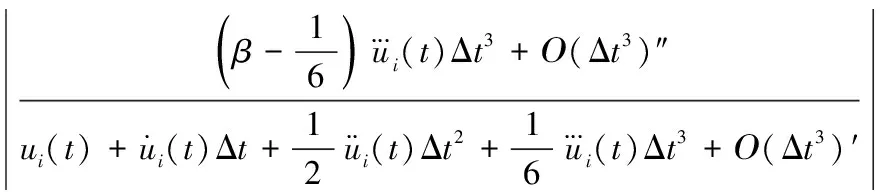
(10)

(11)

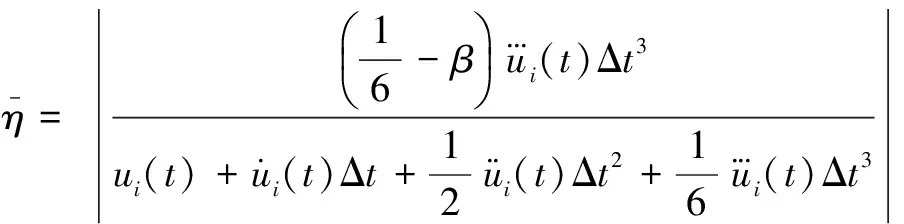
(12)

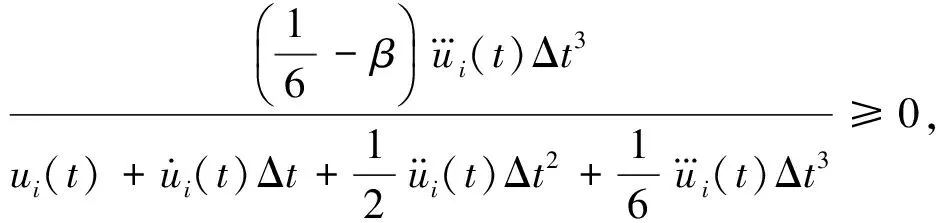
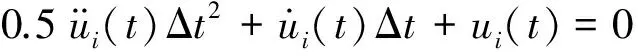
(13)

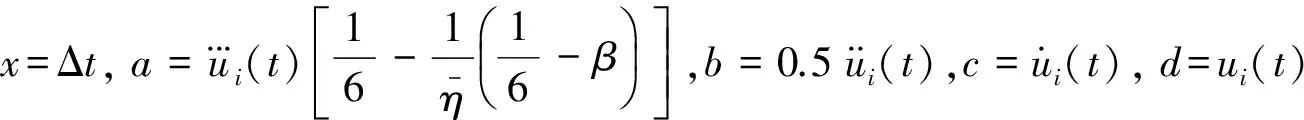
ax3+bx2+cx+d=0

(14)

根据盛金公式

A=b2-3ac,B=bc-9ad,C=c2-3bd,

Δ=B2-4AC

(15)

当A=B=0,式 (13) 的解为

(16)

当Δ=B2-4AC>0,式(13)的解为

(17)

Δt2,3=x2,3=

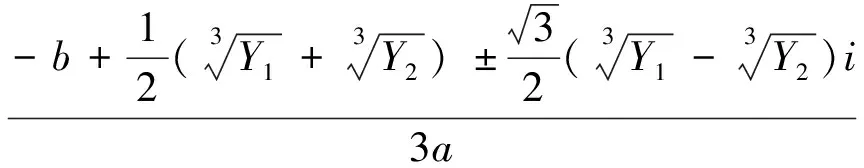
(18)

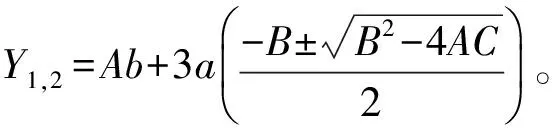
当Δ=B2-4AC=0,式(13)的解为

(19)

(20)

当Δ=B2-4AC<0,式(13)的解为

(21)

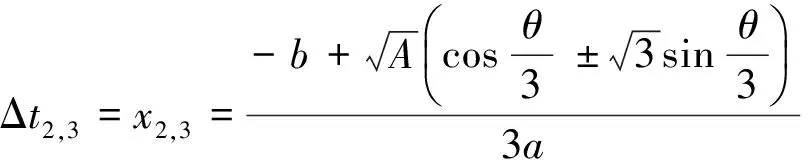
(22)

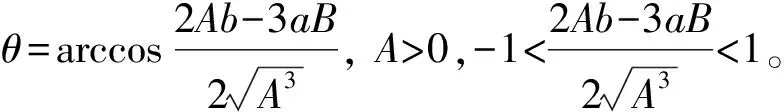
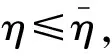
2 有效性验证

为了验证本文方法在提高计算效率方面的有效性，应选取具有解析解的算例进行验证。这里选取Bernoulli-Euler梁作为算例：一个等截面均质的简支梁，初始位移与初始速度均为0，有一个集中力荷载从梁最左端向右端匀速运动，其数值模型如图1所示。

图1 移动荷载下简支梁及节点分布Fig.1 Simply supported beam under moving load and node distribution

移动荷载下Bernoulli-Euler梁运动微分方程[20]

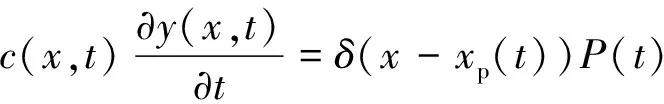
(23)

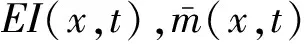
(24)

将梁平均分为20个计算单元，节点分布如图1所示，各节点的初始位移和初始速度均为0，有一个集中力荷载由梁最左端向右端匀速运动。计算参数均假设为无量纲参数(其中L，l分别为梁长和单元长)

EI=100,c=0,L=10,l=0.5,

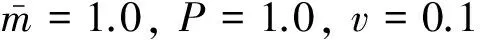
(25)

2.1 计算精度的对比

本文选取梁的11号节点为考察对象，采用固定时间步长为0.08、0.02的Newmark-β法，在固定荷载从3号节点匀速移动到19号节点的时间段内，给出11号节点挠度随时间变化的图形，并与解析解进行了对比，结果见图2。

由固定时间步长为0.08、0.02时的近似解和解析解，按照式(7)计算了11号节点挠度相对误差随时间变化的结果，见图3。

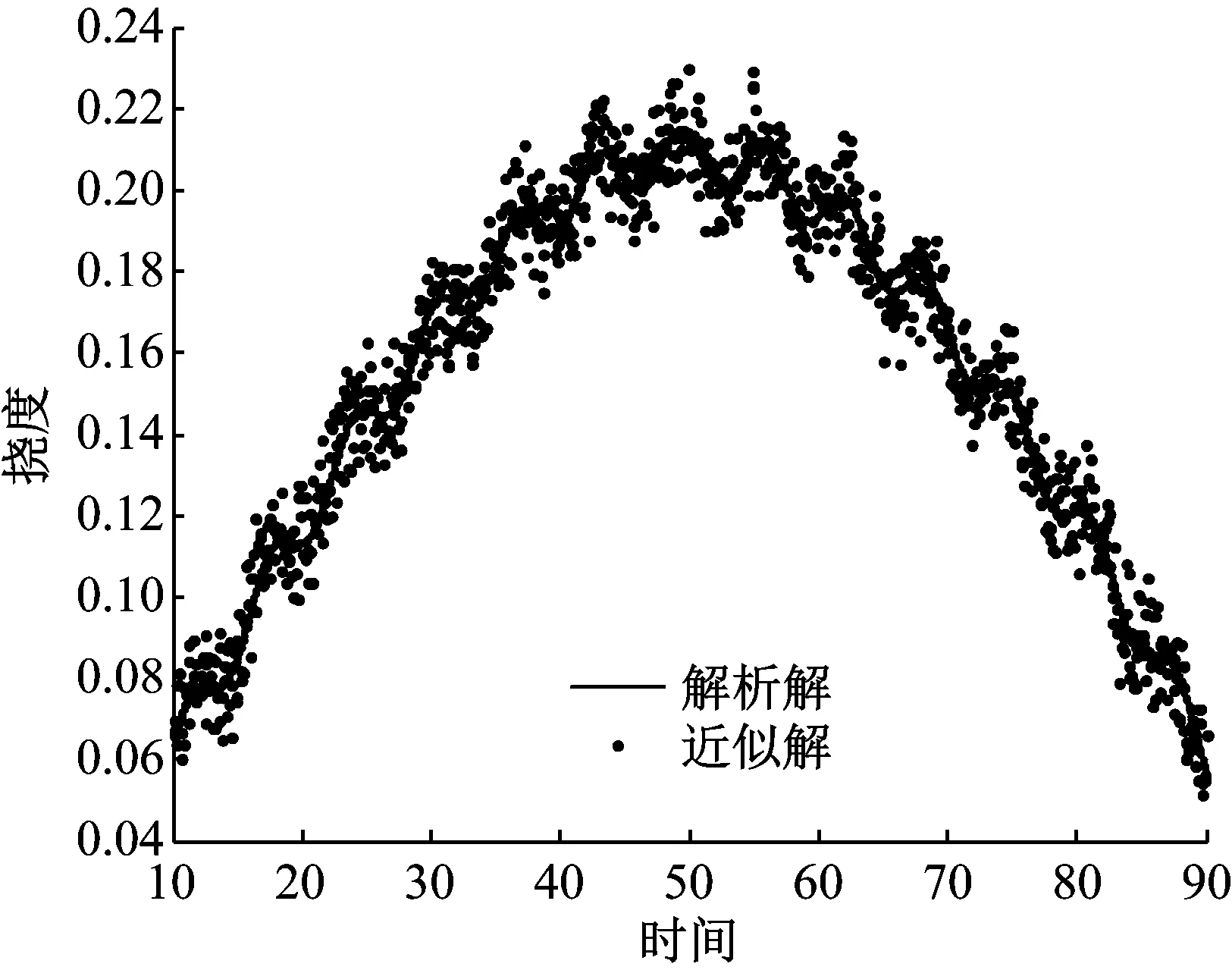
(a) 时间步为0.08

(b) 时间步为0.02图2 11号节点挠度Fig.2 The node 11 deflection

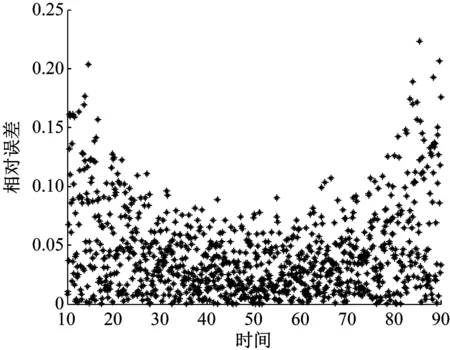
(a) 时间步为0.08

(b) 时间步为0.02图3 Newmark-β法的相对误差Fig.3 Relative error of Newmark-β method

从图2、图3中可以看出，取固定时间步长为0.08时挠度的近似解和解析解相差较大，相对误差最大为0.225。当时间步长取为0.02时，近似解与解析解已经非常接近，相对误差最大仅为0.005 5。这里，选择固定步长为0.02的Newmark-β法的计算结果，与本文方法的计算结果进行对比。从图3(b)中可以看出，步长为0.02时相对误差在0～0.005 5的范围内变动，当相对误差取得最大时所对应的计算精度就是Newmark-β法在固定步长为0.02时所达到的计算精度。

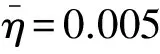
从图4中可以看出相对误差都集中在0.005附近变动，这是由于在式(12)的推导过程中，省略了Ο(Δt3)′、Ο(Δt3)″所致；最大的相对误差为0.005 3，与固定步长为0.02时Newmark-β法的最大相对误差0.005 5基本保持一致。将图3与图4比较可以看出，时间步预判方法可以把相对误差控制在很小的范围内变化，而Newmark-β法无法实现这一点。

图4 时间步自动调整后的相对误差Fig.4 Relative error after time step automatic adjustment

2.2 计算时间的对比

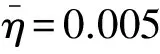
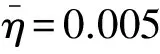
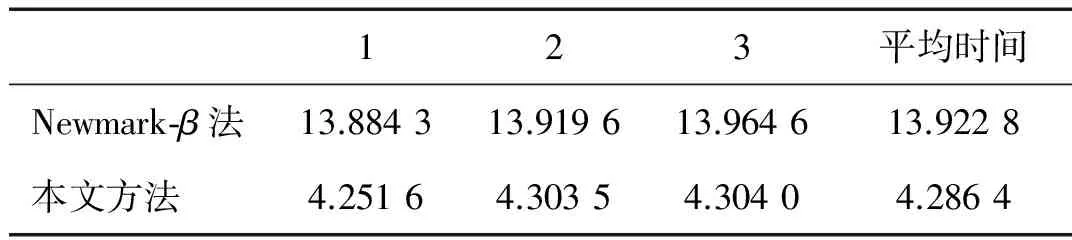
表1 计算时间对比Tab.1 Comparison of computation time s

从上面的分析可以得到：与传统的时间离散方法Newmark-β法相比，本文采用的方法在保证计算精度的同时，节省了69.21%的计算时间，显著的提高了计算效率，并且可以把相对误差控制在很小的范围内变化，具有明显的优越性。

3 荷载与自适应时间步长的关系

文中方法是取Newmark-β法的解做为近似解推导得来的，而Newmark-β方法的推导是基于对加速度的一种假设，加速度是外荷载引起的(内力不计)，那么就有必要对荷载与时间步长的关系进行探讨。

Bernoulli-Euler梁算例在这个问题上，得出的结果过于复杂，很难直接看出荷载与时间步长的变化关系。为了更好的研究这个问题，本文构造了一个受力体的简单模型：物体A，质量为m，在光滑水平面上由静止开始运动，水平方向上仅受P的作用，如图5所示。

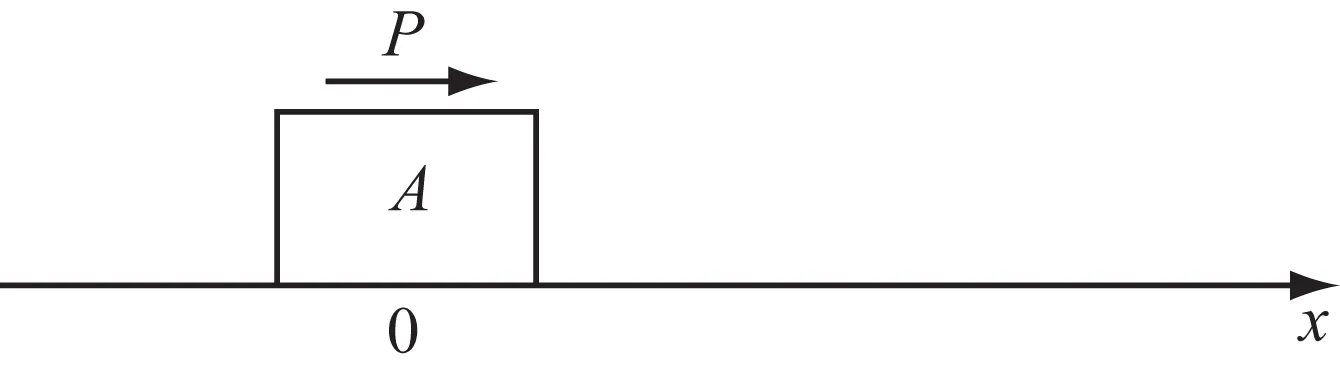
图5 简单模型Fig.5 A simple model

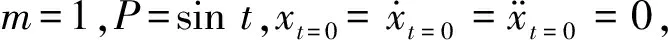
x=t-sint

(26)

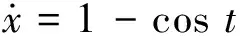
(27)

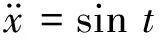
(28)

(29)

图6 时间步长随时间的变化Fig.6 Time step change over time

从图6、图7中分析可以看出，自适应时间步长的变化与荷载的变化密切相关：荷载变化越快，对应的时间步长越小；荷载变化越慢，对应的时间步长越大。在荷载为0的时刻，变化最快，对应的时间步长取得局部最小；在荷载取得最大值的时候，变化最慢，对应的时间步长取得局部最大。所以本文方法，可以反映自适应时间步长变化与荷载变化的关系，做到步长的调整与荷载变化同步，能够反映荷载变化快慢的真实历程。

在传统时间离散方法中，时间步长是固定的，选择不合适的时候会导致计算结果发散或者计算突然终止，当缩小时间步长到一定程度后，才能得到满意的计算结果。产生这个问题的主要原因就在于此：在某一时间步内，荷载变化剧烈，再以原固定步长进行计算会产生较大的误差，这个较大的误差可能会导致后续计算结果的发散，如果误差过大还可能导致计算的突然终止。而在本文方法中，每一步时间步长均是由给定的局部误差限控制得到的，无论荷载如何变化，时间步长都可以自动调整以满足局部误差限的限制，计算不会中断，计算结果始终能满足计算精度的要求。

4 结 论

本文建立了时间步长与相对误差之间的关系，可依此关系计算满足目标误差限的时间步长，作为结构动力时程分析中当前计算步的时间步长，实现了时间步的自动调整，丰富了时间自适应理论研究；与传统的时间离散方法Newmark-β法相比，本文采用的时间自适应方法可以在保证计算精度的同时节省计算时间，显著的提高了计算效率，并能很好的控制相对误差，使其在很小的范围内变动。

通过研究本文方法的自适应时间步长与荷载之间的关系，得出以下结论(内力不计)：荷载变化越快，对应的时间步长越小；荷载变化越慢，对应的时间步长越大。从而证实了该方法可以很好的反映自适应时间步长变化与荷载变化的关系，做到步长的调整与荷载变化同步。

在传统时间离散方法中，时间步长是固定的，选择不合适的时候会导致计算结果发散或者计算突然终止，当缩小时间步长到一定程度后，才能得到满意的计算结果。这主要是因为：在某一时间步内，荷载变化剧烈，再以原固定步长进行计算会产生较大的误差，这个较大的误差会导致后续计算结果的发散，如果误差过大还可能导致计算的突然终止。而在本文方法中，每一步时间步长均是由给定的局部误差限控制得到的，无论荷载如何变化，时间步长都可以自动调整以满足局部误差限的限制，计算不会中断，计算结果始终能满足计算精度的要求，并且计算时间还能大大的节省，这些都说明该方法在数值计算中具有重要意义。

参 考 文 献

[1] 王林, 蔡改改, 高冠琪. 基于改进MP的稀疏表示快速算法及其滚动轴承故障特征提取应用[J]. 振动与冲击, 2017, 36(3): 176-182.

WANG Lin, CAI Gaigai, GAO Guanqi. Fast sparse representation algorithm based on improved MP and its applications in fault feature extraction of rolling bearings[J]. Journal of Vibration and Shock, 2017, 36(3): 176-182.

[2] 祝志文, 黄炎. 大跨度桥梁脉动风场模拟的插值算法[J]. 振动与冲击, 2017, 36(7): 156-163.

ZHU Zhiwen, HUANG Yan. Interpolation algorithm for fluctuating wind field simulation of long-span bridges[J]. Journal of Vibration and Shock, 2017, 36(7): 156-163.

[3] 张斌, 雷晓燕, 罗雁云. 基于Newmark格式的车辆-轨道耦合迭代过程的改进算法[J]. 中南大学学报(自然科学版), 2016, 47(1): 298-306.

ZHANG Bin, LEI Xiaoyan, LUO Yanyun. Improved algorithm of iterative process for vehicle-track coupled system based on Newmark formulation[J]. Journal of Central South University (Science and Technology), 2016, 47(1): 298-306.

[4] 张弛, 贾丽媛, 王加阳. 改进的混合免疫算法在约束函数优化中的应用[J]. 中南大学学报(自然科学版), 2016, 47(6): 1940-1946.

ZHANG Chi, JIA Liyuan, WANG Jiayang. An improved hybrid immune algorithm for multimodal optimization[J]. Journal of Central South University (Science and Technology), 2016, 47(6): 1940-1946.

[5] SLOAN S W, ABBO A J. Biot consolidation analysis with automatic time stepping and error control, Part 2: applications[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1999, 23(6): 493-529.

[6] ZIENKIEWICZ O C, XIEY M. A simple error estimator and adaptive time stepping procedure for dynamic analysis[J]. Earthquake Engineering & Structural Dynamics, 1991, 20(9): 871-887.

[7] ZENG L F, WIBERG N E, LI X D. A posteriori local error estimation and adaptive time-stepping for newmark integration in dynamic analysis[J]. Earthquake Engineering & Structural Dynamics, 1992, 21(7): 555-571.

[8] WIBERG N E, LI X D. A post-processing technique and an a posteriori error estimate for the newmark method in dynamic analysis[J]. Earthquake Engineering & Structural Dynamics, 1993, 22(6): 465-489.

[9] TANG G, ALSHAWABKEH A N, MAYES M A. Automatic time stepping with global error control for groundwater flow models[J]. Journal of Hydrologic Engineering, 2008, 13(9): 803-810.

[10] KAVETSKI D, BINNING P, SLOAN S W. Adaptive backward Euler time stepping with truncation error control for numerical modelling of unsaturated fluid flow[J]. International Journal for Numerical Methods in Engineering, 2002, 53(6): 1301-1322.

[11] KUO S R, YAU J D, YANG Y B.A robust time-integration algorithm for solving nonlinear dynamic problems with large rotations and displacements[J]. International Journal of Structural Stability and Dynamics, 2012, 12(6):1250051-(1-24).

[12] 王开加, 程建生, 段金辉. 基于时间步长自适应技术的海上浮基风电平台绕流数值模拟分析[J]. 船舶与海洋工程, 2013(2): 52-57.

WANG Kaijia, CHENG Jiansheng, DUAN Jinhui. Numerical simulation analysis of offshore floating wind power generation platform based on time step adaptive method[J]. Naval Architecture and Ocean Engineering, 2013(2): 52-57.

[13] 毛卫南, 刘建坤. 自适应时间步长法在土体冻结水热耦合模型中的应用[J]. 防灾减灾工程学报, 2014, 34(4): 510-516.

MAO Weinan, LIU Jiankun. Application of adaptive time step method to water-heat coupling model of soil freezing[J]. Journal of Disaster Prevention and Mitigation Engineering, 2014, 34(4): 510-516.

[14] TANG X W, ZHANG X W, UZUOKA R. Novel adaptive time stepping method and its application to soil seismic liquefaction analysis[J]. Soil Dynamics and Earthquake Engineering, 2015, 71(4): 100-113.

[15] ZHANG X W, TANG X W, UZUOKA R. Numerical simulation of 3D liquefaction disasters using an automatic time stepping method[J]. Natural Hazards, 2015, 77(2): 1275-1287.

[16] NAVEED A, VOLKER J. Adaptive time step control for higher order variational time discretizations applied to convection-diffusion-reaction equations[J]. Comput Methods Appl Mech Engrg, 2015, 285: 83-101.

[17] VAHID Z R, SHEN Y X. Massive parallelization of the phase field formulation for crack propagation with time adaptivity[J]. Comput Methods Appl Mech Engrg, 2016, 312: 224-253.

[18] MARC L, SERGE P, KRISTOFFER G Z. Preface to the special issue on error estimation and adaptivity for nonlinear and time-dependent problems[J]. Comput Methods Appl Mech Engrg, 2015, 288: 1.

[19] BROWN M J M B. The discretization error of Newmark’s methods for numerical intergration in structural dynamics. Earthquake Engineering & Structural Dynamics, 1985, 13: 43-61.

[20] LIN Y H, TRETHEWEY M W. Finite element analysis of elastic beams subjected to moving dynamic loads[J]. Journal of Sound and Vibration, 1990, 136(2): 323-342.

[21] FRYBA L. Vibration of solids and structures under moving loads[M]. London: Thomas Telford, 1999.