复合载荷作用下火箭输送管动力特性试验与数值研究

韩文龙， 张明明， 卫 国， 胡彦平， 王 帅(北京强度环境研究所 环境可靠性中心，北京 100076)

大推力新型运载火箭动力系统多采用无毒无污染的液氢液氧或液氧煤油发动机，低温推进剂的使用给火箭增压输送系统的设计与实施带来巨大的挑战和技术难题。输送管作为增压输送系统关键组成部分，担负着推进剂输送的核心任务，且管路在箭上实际工作过程中受到内压、低温、振动、冲击、复杂边界等综合工况的影响[1-3]。因此研究输送管在综合工况下的结构动力特性，保障输送管在工作过程中的可靠性尤为重要。

近年来综合工况下管路动力特性研究主要集中在充液管路的流固耦合研究[4-8]、增压管路的气固耦合研究[9-11]以及不同温度环境对管路动力特性的影响[12-15]。以上研究主要侧重于结构简单、内径较小的管路，方法上也偏重于数值模拟和仿真计算。对于大推力新型运载火箭输送管，由于管路内径大，且同时受到低温、高压、振动等综合应力作用，因此无论试验还是仿真计算方面的相关研究都很少，特别是试验方面由于其难度大，复杂性强、危险系数高、试验成本高，国内鲜有成功案例。本文根据输送管路在箭上的实际安装及工作状态，设计了一整套综合试验系统，攻克了各类技术难关开展了相关试验，并依据试验分析结果建立并修正了管路有限元模型，结合试验对管路在箭上所经受的复合环境应力进行了仿真和试验研究。

1 理论基础

本项目研究对象为两端通过法兰盘封闭空间管路，内部充压的氮气和液氮作为管路的内部载荷，因此不考虑气体和液体的流速影响。

振动试验中，空间管路系统一端固定在振动台上，其他端都与钢梁或铸块固定。因此，可将空间管路系统简化为一端固支，一端施加外部给定运动激励的动力学模型其动力学方程为

(1)

考虑管路内部充气压，空间管路呈现预紧力状态，表现为刚度提升，此时的动力学方程为

([Kp]+[ΔK]){x}={f}

(2)

管路内部充满一定压力的液体时，液体作为附加质量明显改变空间管路系统的结构的动特性，造成管路结构质量、阻尼发生变化，此时系统的动力学方程为

([Kp]+[ΔK]){x}={f}

(3)

当管路结构承受温度载荷时(液氮80 K温区)，结构的刚度也会发生变化，从而影响结构的动力学特性。温度载荷对结构刚度的影响体现在两个方面：① 材料的弹性模量随温度变化而变化；② 结构中的存在温度梯度会产生热应力，从而改变结构的刚度，此时系统的动力学方程为

([Kp]+[ΔK]+[ΔK′]){x}={f}

(4)

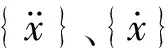
2 试验研究

2.1 试验系统设计及搭建

由于输送管在箭上的实际安装状态为一端与发动机端口相连接，一端与储箱相连接。为能更加真实的模拟箭上安装状态、边界条件，以及发动机工作时输送管所处的真实工况环境，试验时管路与发动机连接端为激励端，与储箱系统连接端为固支端。试验中，低温加载使用液氮加注，压力加载使用高压氮气瓶充压，同时利用压力平衡器保证试验过程中管路系统内部压力始终处于动态平衡状态。加压过程中由于管路内径大，管路内部所受内压载荷会随着压力的变大而不断加大，且管路中间波纹软管会随着内压的增加刚度逐渐变大，此时管路极易发生侧翻失稳，因此试验中设计了承力和防失稳系统。具体试验系统，如图1～图3所示。

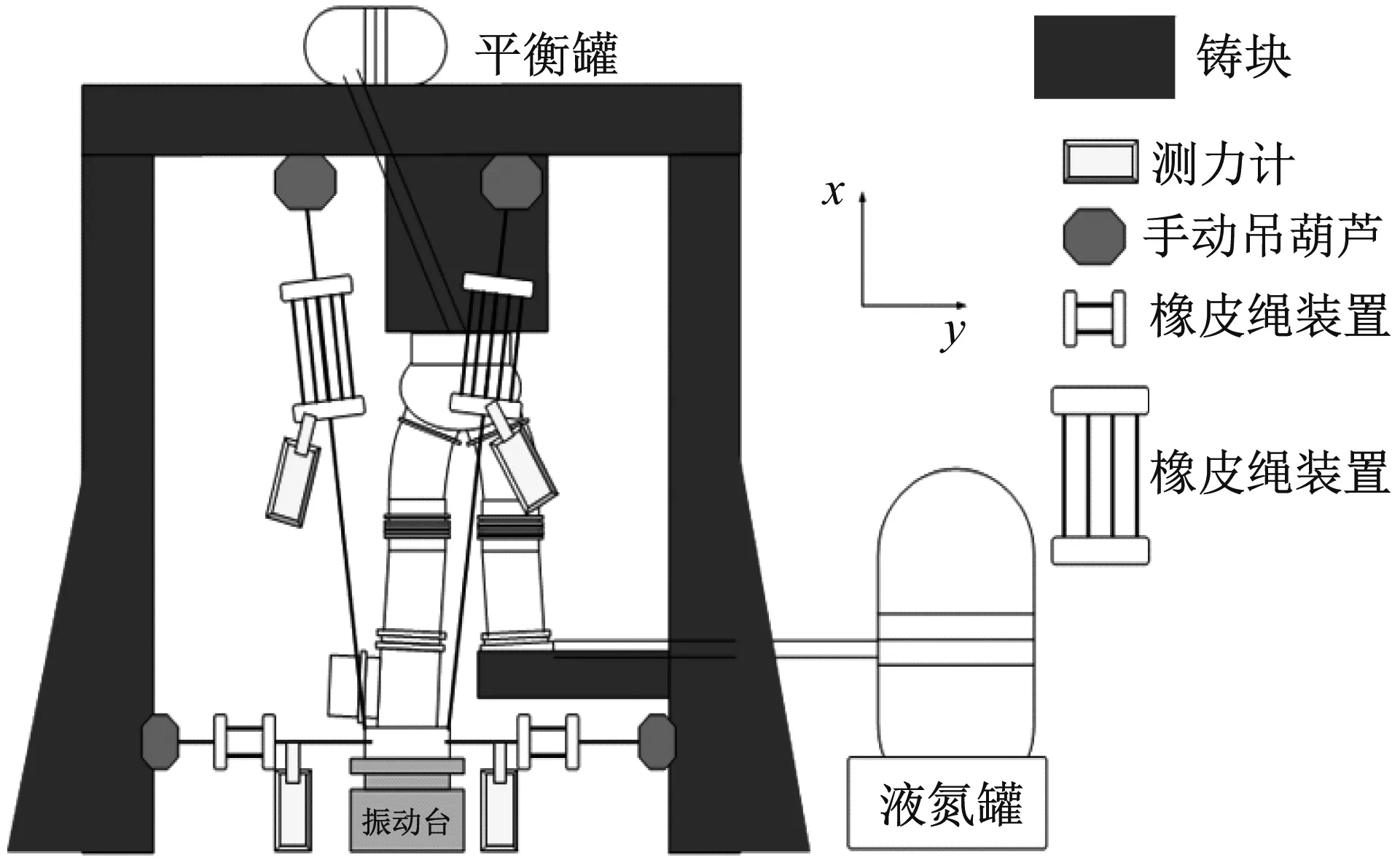
图1 试验系统示意图Fig.1 Schematic diagram of the test system

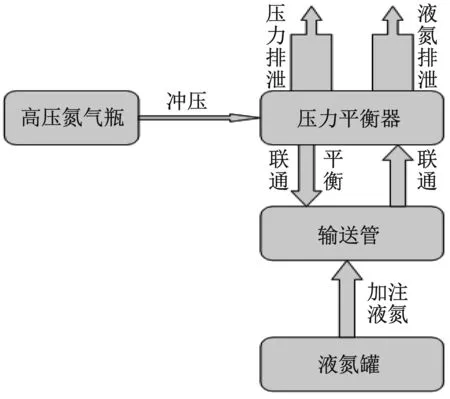
图2 试验装置简要操作流程Fig.2 Brief description of the test device

具体试验时，由于输送管和压力平衡器可看成一套连通器，因此试验操作时首先使用高压氮气瓶经压力平衡器对输送管进行氮气置换，以保证管内介质单一；其次使用液氮加注系统对输送管进行低温液氮加注，直至压力平衡器自动排液阀打开，表明液氮加注已满，同时通过温度传感器观察温度。

图3 管路试验状态Fig.3 Pipeline test status

2.2 两种状态下应变变化趋势

应变在常温状态和低温状态下随压力变化趋势如图4所示。

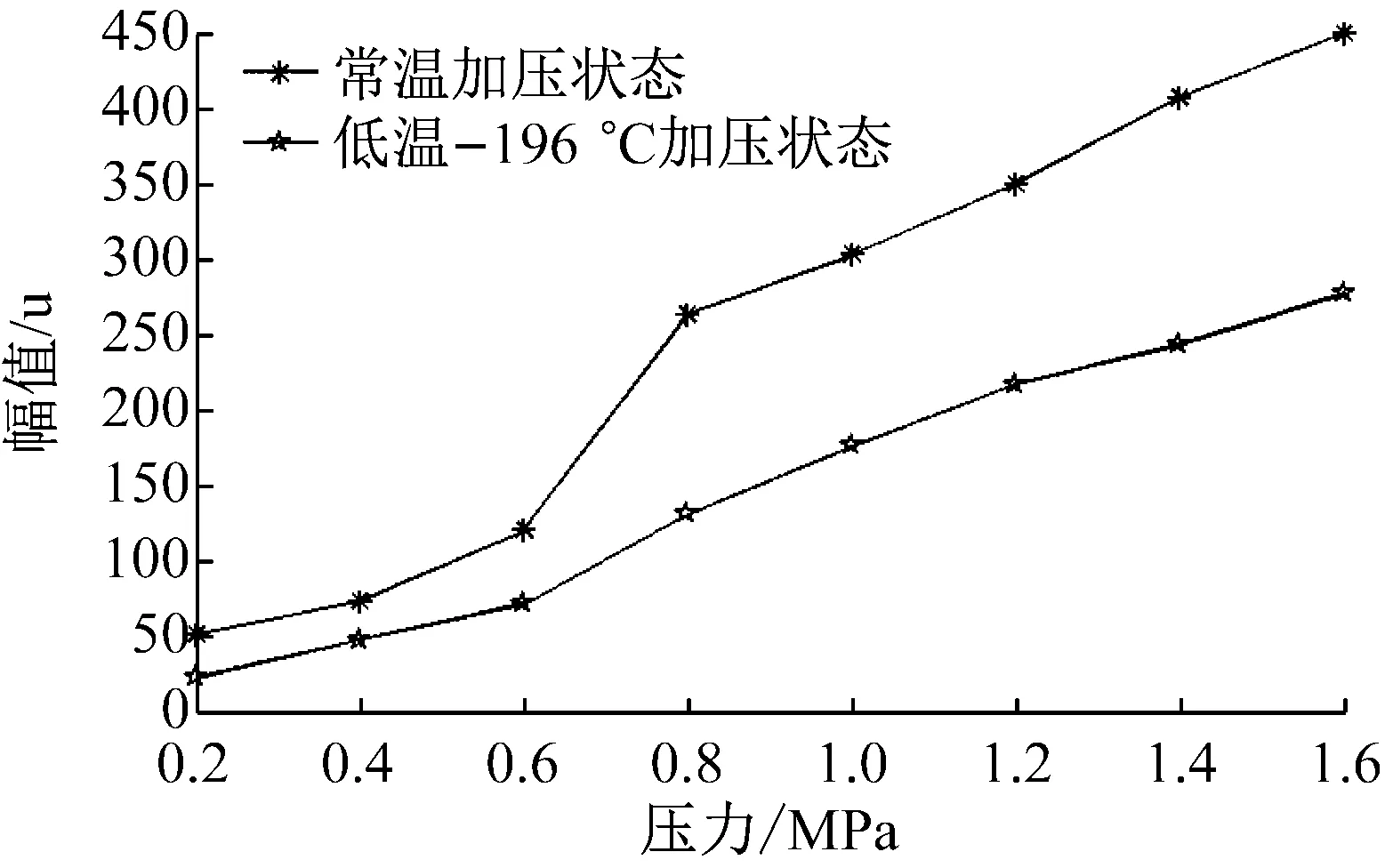
图4 不同工况下应变随压力变化趋势Fig.4 Change trend of strain with pressure under different working conditions

图4为波纹管上端5#点附近的应变变化趋势图，分析其他应变测点也可得到相似变化趋势，比较上图两条曲线可以看出应变在常温状态和低温状态下随压力的逐步增加而逐渐变大，但常温状态下比低温状态下在同压力下的应变相对值大，且受压力变化的影响更大。分析原因，常温状态下管路内部充压，管路刚度变大，空间管路呈现预紧力状态，因此应变逐渐随压力的变大而变大；低温状态下管路性能更加优异，相比常温管路在低温状态下其强度、塑性、韧性都大幅度提高，因此低温状态下管路受压力的影响没有常温下大。

2.3 不同工况下管路固有频率研究

对管路做研究性小量级随机振动试验，带宽为(20～1 000 Hz)。常温常压状态、常温加压状态(1.0 MPa)、液氮低温加压状态(1.1 MPa/-196 ℃ )下管路波纹管上端测点与台面传递函数曲线，如图5所示。固有频率，如表1所示。

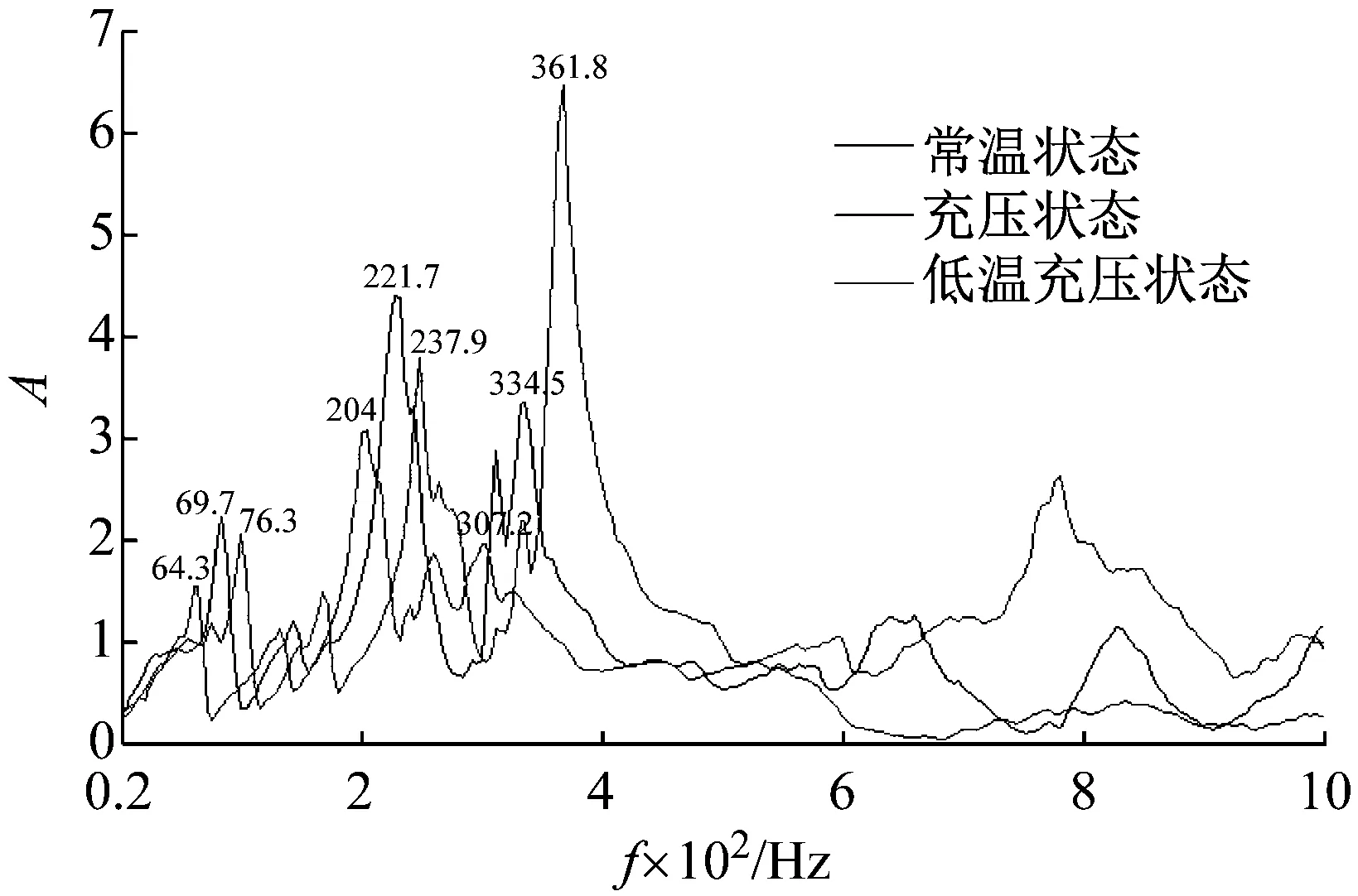
图5 不同工况下传递函数曲线Fig.5 Transfer function curves under different operating

图5和表1为波纹管上端加速度曲线和固有频率值，分析其他加速度测点也可得到相似变化趋势，因此说明这种变化趋势对此类管具有路普适特性。由图5和表1可知，相对于常温常压下管路固有频率，低温常压状态下管路固有频率出现显著前移，常温充压状态下管路固有频率出现显著后移。由此可以判断，常温充压使得管路刚度变大，质量变化可忽略，因此固有频率变大。低温充压状态下管路受压力影响刚度变大，受温度影响结构的刚度也会发生变化，从而影响结构的动力学特性，温度载荷对结构刚度的影响体现在两个方面：①材料的弹性模量随温度变化而变化；②结构中存在的温度梯度会产生热应力，从而改变结构的刚度；同时低温状态下管路充满液氮，管路的整体质量显著变大，最终使得刚度、质量的比值相对变小，因此低温充压状态下固有频率变小。

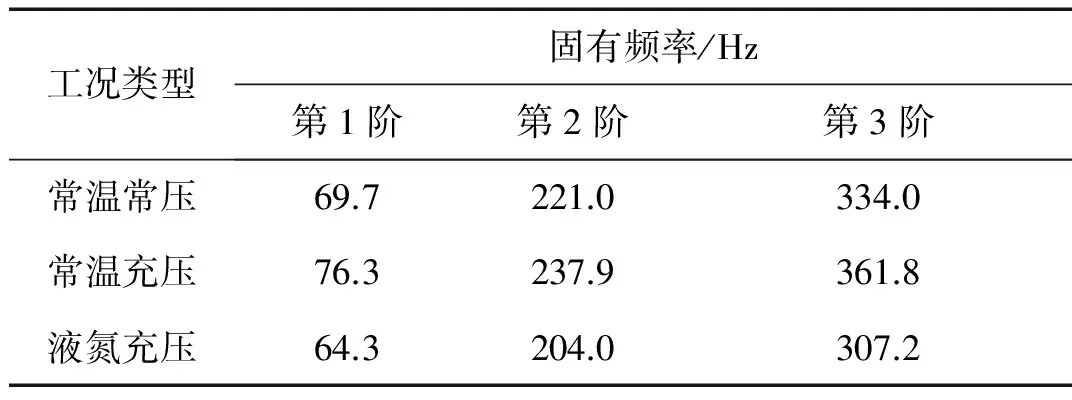
表1 各工况下固有频率值Tab.1 Natural frequencies under differentoperating conditions

3 有限元建模及仿真

3.1 输送管有限元模型

依据管路几何模型及试验状态建立管路结构有限元模型，并参考试验结果对有限元模型进行修正，首先利用常温常压状态下小量级随机振动所得到的前十阶模态，对管路各位置厚度进行灵敏度分析，其结果如图 6所示。再根据不同状态下管路的结构固有特性差异，对管路有限元模型进行了差异化修正。修正后的模型，如图7所示。其中A端面和C端面固支，B端面为振动台激励输入端。计算时有限元模型采用4边形壳单元(CQUAD4)建立，材料参数属性如表2所示；管路在液氮充压状态下，温度、内压等均以预应力的形式考虑，通过预应力修正结构刚度，最后将修正后的刚度矩阵施加于有限元模型，对于管路内的液氮以分布式附加质量效应加载于模型上。试验测点2#、4#、6#在1#、3#、5#的对称面，且各测点分别对应相同位置的有限元节点编号。

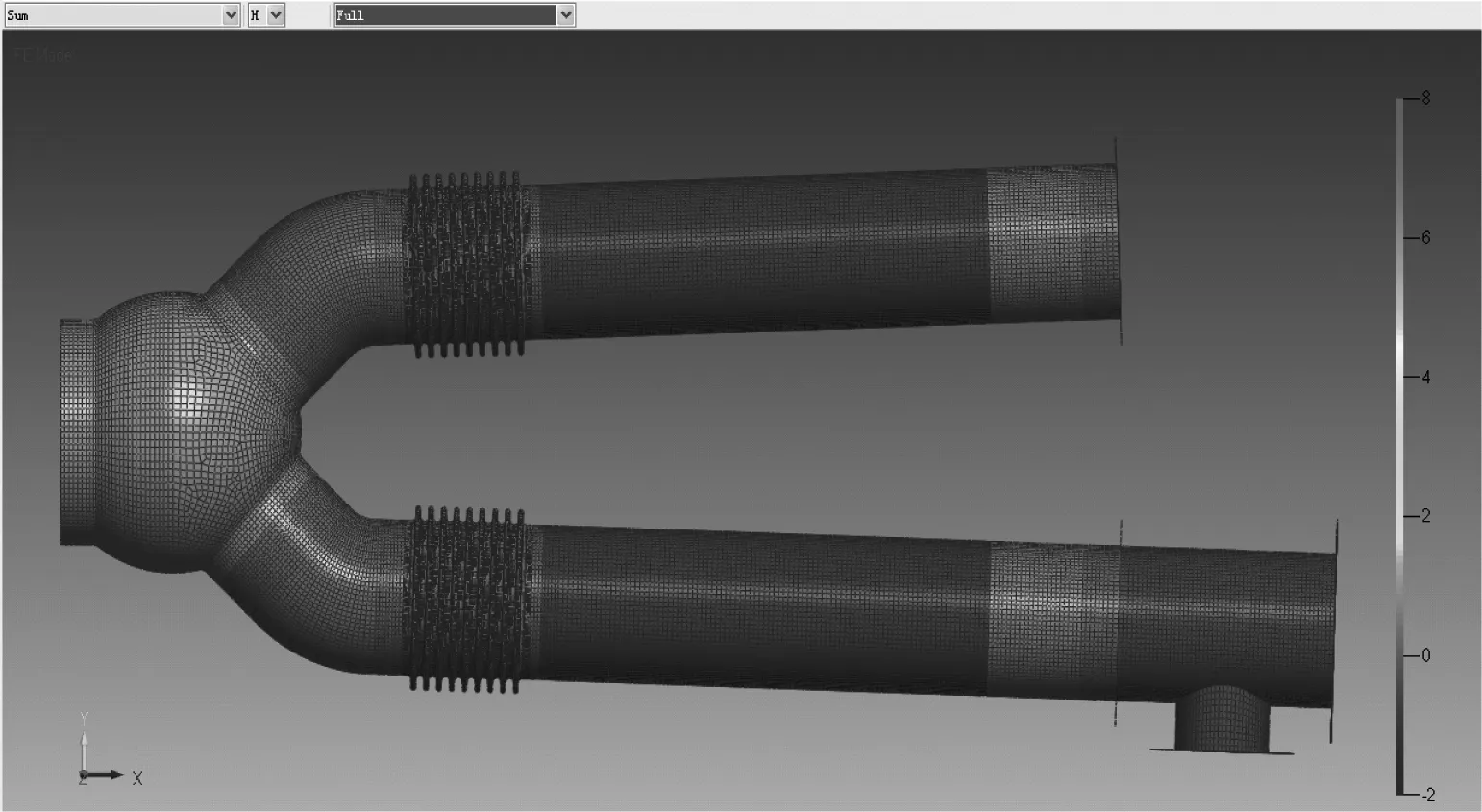
图6 管路前十阶模态对厚度的灵敏度Fig.6 Sensitivity of the ten-step mode to thickness of the pipe

表2 材料参数属性Tab.2 Material parameter attributes

图7 输送管有限元模型Fig.7 Finite element model of the pipe

3.2 仿真与试验结果分析

利用前节修正得到的有限元模型，计算了在温度-196 ℃、内压为1.1 MPa复合预载荷作用下，20～2 000 Hz频带内随机振动条件下各测点加速度功率谱密度分布，并与试验结果进行了比对。图8和图9分别为1#、2#、3#、4#测点的计算及试验结果。图10为管路各测点总均方根值变化趋势的计算与试验结果比对图。

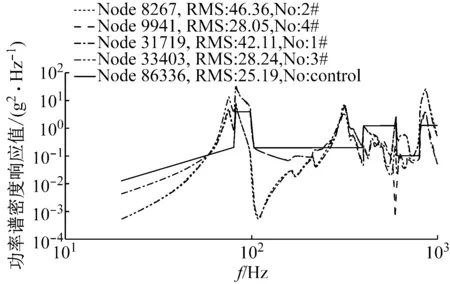
图8 加速度测点频响函数仿真结果Fig.8 Simulation results of frequency response function of acceleration point

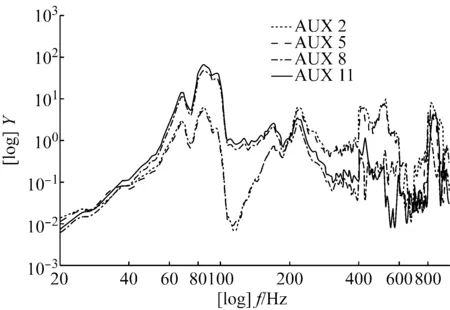
图9 加速度测点频响函数试验结果Fig.9 Test results of frequency response function of acceleration point

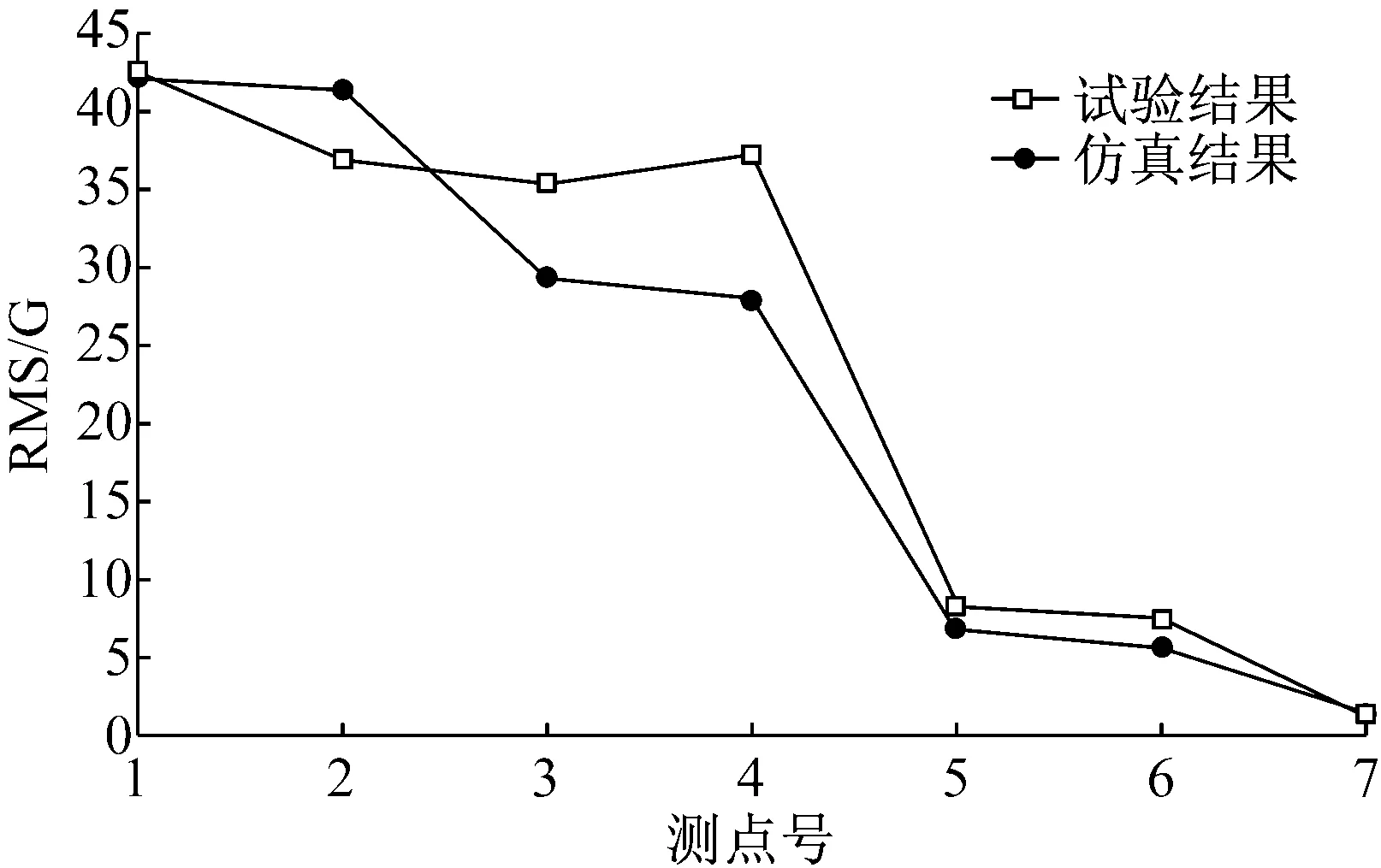
图10 加速度测点总均方根值变化曲线Fig.10 Curve of total root mean square change of acceleration point

由图7～图9可知，试验结果与数值计算结果吻合较好，波纹管下方(1#～4#测点区域其中，图9中AUX2～AUX11为试验时1#～4#点的测量通道)在此方向上的加速度响应曲线传递趋势基本一致，响应量级相近，最大实测响应与计算响应均为42g左右，与输入量级25g相比放大约为4.5 dB。经波纹管位移补偿后，三通及其分支根部(5#～7#)加速度响应量级有一定的衰减，试验测量最大值约为7g(-11 dB)，仿真结果为6g(-12 dB)。由图9整体来看加速度响应沿管路由振动端向固支端呈现逐级递减趋势，且经波纹管后响应呈显著衰减趋势。

4 结 论

(1)设计并搭建了复合振动试验系统，解决了试验中低温加载、压力平衡、管路极限位移补偿、管路变形失稳防防护等一系列技术难题；实现了地面试验对大内径液氧输送管箭上工作状态尽可能真实模拟。

(2)分析了常温和低温状态管路应变随压力的变化趋势，研究了管路在常温常压、常温充压、低温充压三种状态下固有频率，得出f(常温充压)>f(常温常压)>f(低温充压)。

(3)依据试验结果建立并修正了管路有限元模型，结合试验分析了管路在复合随机振动条件下各部位加速度响应，验证了有限元模型的正确性，得到了管路不同位置的加速度变化趋势，为后续研究奠定了基础。

参 考 文 献

[1] 王其政.结构耦合动力学[M].北京:宇航出版社, 1997.

[2] 王心清.液体弹道导弹与运载火箭系列[M].北京：宇航出版社，1994.

[3] Department of Defense． Environment engineering consideration and laboratory tests: MIL-STD-810G[S]．Dayton, OH: Aeronautical Systems Center，2008: 20-34．

[4] 邱明星，陈志英，王建军.充液管路固有频率试验与计算分析[J].推进技术，2013，24(11):37-42.

QIU Mingxing，CHEN Zhiying, WANG Jianjun. Experiment and numerical analysis of natural frequency for liquid-filled pipe[J]. Journal of Propulsion Technology，2013，24(11):37-42.

[5] 卢丽金，黄超广，沈祖辉. 飞机液压/燃油管路系统振动故障模式、机理及排除方法[J]. 振动工程学报，2008，21(9)：78-81.

LU Lijin，HUANG Chaoguang，SHEN Zuhui. Aircraft hydraulic/fuel piping system failure modes of vibration mechanism and trouble shooting[J]. Journal of Vibration Engineering，2008，21(9)：78-81.

[6] 张立翔，黄文虎，TIJSSELING A S. 管路流固耦合振动研究进展[J]. 水动力学研究与进展，2000，15(3)：366-379.

ZHANG Lixiang，HUANG Wenhu，TIJSSELING A S. Progress of conveying fluid pipe in fluid-structure interaction[J]. Journal of Hydrodynamics，2000，15(3)：366-379.

[7] MIRRAMEZANI M，MIRDAMADI H R，GHAYOUR M. Innovative coupled fluid-structure interaction model for carbon nano-tubes conveying fluid by considering the size effects of nano-flow and nano-structure[J].Computational Materials Science， 2013，77：161-171.

[8] KARAGIOZIS K N，PAIDOUSSIS M P，AMABILI M. Effect of geometry on the stability of cylindrical clamped shells subjected to internal fluid flow[J]. Computers and Structures，2007，85：645-659.

[9] 李林凌, 黄其柏, 连小珉, 等. 排气管气固耦合系统振动特性[J].汽车工程, 2006, 28(12): 1078-1085.

LI Linling, HUANG Qibai, LIAN Xiaomin, et al. Vibration characteristics of gas structure coupling system of exhaust pipeline[J]. Automotive Engineering, 2006, 28(12): 1078-1085.

[10] 郭长虹，丁旭，曹源，等.页岩气井下开采管路气固耦合振动特性分析[J].液压与气动, 2016, 7(10): 50-55.

GUO Changhong, DING Xu, CAO Yuan, et al. Gas-solid coupling vibration characteristics analysis of underground mining shale gas pipeline[J]. Chinese Hydraulics & Pneumatics, 2016, 7(10): 50-55.

[11] 赵杰，李峰，刘录． 超高压管线系统气固耦合振动特性的仿真研究[J]．北京石油化工学院学报， 2013(2): 26-29．

ZHAO Jie，LI Feng，LIU Lu． Simulation of ultra-high pressure pipeline system vibration characteristics of gas solid coupling[J].Journal of Beijing Institute of Petro-Chemical Technology，2013(2): 26-29．

[12] 程谋森, 刘昆, 张育林. 低温推进剂供应管路预冷充填瞬变流计算[J].推进技术, 2000, 21(5): 38-41.

CHENG Mousen, LIU Kun, ZHANG Yulin. Numerical analysis of precooling and priming transients in cryogenic propellant feed systems[J]. Journal of Propulsion Technology, 2000, 21(5): 38-41.

[13] 任德鹏，丁鹏飞，夏新林.低温液体充填管路的数值计算[J].工程热物理学报, 2004, 25(1): 118-120.

REN Depeng, DING Pengfei, XIA Xinlin. Numerical simulation of filing process of cryogenic liquid in a pipeline.[J]. Journal of Engineering Thermos-Physics, 2004, 25(1): 118-120.

[14] LANKFORD D W, SIMMONS M A, HEIKKINEN B D. A detailed numerical simulation of a liquid propellant rocket engine ground test experiment[R]. AIAA 92-3604.

[15] SCHLEY C A, GOLOVITCHEV V, HAGEMANN G. Comparison of high pressure H2/O2 rocket model engine reference simulation[R]. AIAA 95-2429.