制造的斜齿轮齿向修形曲线的优化分析
崔雪莹,操 兵,刘鹏祥
(1.中国航发哈尔滨东安发动机有限公司,黑龙江 哈尔滨 150066;2.重庆大学机械传动国家重点实验室,重庆 400044)
0 引言
齿轮齿向修形是沿齿线方对齿面进行微量修整,使齿面形状与理论形状产生一定量的偏差。齿向修形能够减少由于受载后齿形、齿向畸变和制造、安装误差所造成的齿顶啮合冲击以及偏载等情况,能够降低传动系统的噪音,延长齿轮的服役时间。
目前,海内外专家学者对渐开线齿轮的齿向修形进行了大量的研究。在齿向修形的设计方面:通过研究载荷沿接触线的分布规律,提出了齿轮齿向修形优化设计方法[1]。在考虑齿轮轮体的弯曲扭转变形、齿面弹性变形及齿面误差的基础上,提出了齿向修形量的计算方法[2]。基于齿轮副所有接触载区域载荷之和等于总载荷的假设,提出计算鼓形修整理论修整量的计算方法。在修形齿轮的加工方面:采用附加径向运动对拓扑修形斜齿轮进行成形磨齿,提出了一种减小成形磨齿误差的砂轮廓形优化方法;在分析了齿向修形与接触线间的关系、砂轮安装参数与接触线间的关系的基础上,提出了一种提高优化成形磨齿接触线的方法,进一步提高了成形磨齿的精度。
综上所述,在齿向修形的修形曲线的设计,修形量的确定以及修形齿轮的加工等方面均有相关的研究。但目前所有齿向修形的设计均只考虑了修形对传动性能的影响,并未考虑给常用齿轮加工方式带来的困难。蜗杆砂轮磨削作为中小模数齿轮的主要的加工方式,其在加工齿向修形的斜齿轮时存在原理性误差,产生齿面扭曲,严重制约了齿轮精度的进一步提升。还未发现从蜗杆砂轮磨削修形齿轮工艺角度研究齿轮修形存在的问题。
在分析了齿面扭曲产生机理以及建立鼓形修形量与齿面扭曲量对应的关系模型后,本文提出一种齿向鼓形修形曲线的优化方法。并以蜗杆砂轮磨削某齿向修形斜齿轮为例,计算了齿向鼓形修形曲线优化前后齿面扭曲量,分析了齿面接触应力以及齿向载荷的分布情况。
1 鼓形修形曲线方程及蜗杆砂轮磨削路径设计
在常用的齿向修形方法中,鼓形修形由于设计简单、加工方便而且控制修形质量容易,所以应用范围最广。齿向鼓形修整的目的是避免啮合齿轮副在两端发生点接触;同时使载荷在齿宽方向上分布均匀。
1.1 齿向修形曲线方程
齿向鼓形修形是设计一条齿向曲线使齿轮在两端齿厚变小,中间鼓起,如图1所示。以齿轮分度圆柱截齿廓所得曲线为研究对象,当没有齿向修形时,所得曲线是一条螺旋线,图2为鼓形修形曲线示意图。

图1 齿向鼓形修形示意图

图2 鼓形修形曲线
令鼓形修形曲线的鼓点在齿宽中部,此处修形量为0;齿轮两端的修行量为g,则鼓形修形曲线的方程为:

式中:ρ为抛物线系数,g是齿轮参数与最大修形量的函数;z为自变量,其取值范围为
1.2 蜗杆砂轮磨削修形齿轮路径设计
蜗杆砂轮磨削齿向修形斜齿轮是通过改变砂轮磨削轨迹实现的。蜗杆砂轮沿齿轮径向的附加运动(X轴运动)和沿齿轮切向的附加运动(Y轴的运动)均可以改变包络出的齿轮廓形的位置。以齿轮节圆上的齿向修形量为准,讨论齿向修形量与蜗杆砂轮沿X、Y轴附加运动量间的关系。
(1)X轴附加移动量
图3是X轴附加运动示意图。图中Pa是修形前齿轮端面廓形。

图3 X轴附加运动
当齿轮在该端面的齿向修形量为G(z),蜗杆砂轮在该位置的X轴的附加移动量Δx与G(z)间的关系为:

式中:β为齿轮的螺旋角,α为齿轮端面压力角。
蜗杆砂轮沿X轴的附加移动将使齿轮左右齿廓相对于齿槽对称面的偏移量相同。所以,X轴的附加移动对齿轮左右齿廓产生相同的修形量。
(2)Y轴附加移动量
图4是蜗杆砂轮沿Y附加运动与所加工的齿廓间的关系。

图4 Y轴附加运动
Y轴附加移动量Δy与修形量间的关系为:

当蜗杆砂轮沿齿轮切向有附加移动时,将使蜗杆砂轮偏向于齿轮的一个齿面而远离另一个齿面。所以,将对齿轮左右两齿廓产生相反的修形量。
蜗杆砂轮磨齿机是五轴联动数控机床,在加工齿轮过程中,C轴和Y轴具有确定的运动关系。因此,可以将Y轴的附加移动转换成C轴的附加移动。其间的转换关系为:
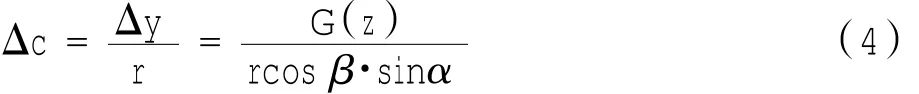
蜗杆砂轮磨削齿向修形齿轮时,通过X轴和Y轴(或C轴)的组合运动,可以实现左右齿面任意的齿向修形。
2 齿面扭曲产生机理及鼓形修形曲线优化方法
2.1 齿面扭曲产生机理
齿面扭曲现象是指齿轮的端面齿廓沿齿宽方向逐渐发生扭转的现象,反映了齿轮各个端面存在不均匀的切除量[a][3]。图5是齿面扭曲的示意图。
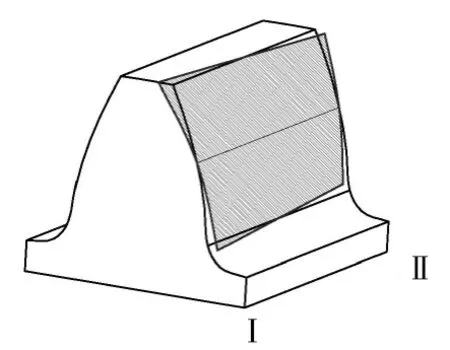
图5 齿面扭曲示意图
蜗杆砂轮磨削渐开线斜齿轮可以看成是一对交错轴斜齿轮的啮合过程[4]。在磨削过程中,蜗杆砂轮与被磨齿轮为点接触,接触点的位置在齿轮齿面上连续变化形成接触迹[5]。将空间的接触迹表示在齿轮基圆柱切平面内,如图6所示。该图中,接触迹将被展成直线,并与齿轮端面的基圆夹角为基圆螺旋角。当齿轮存在齿向修形时,其修形曲线是叠加在齿轮分度圆的螺旋线上,使分度圆上的接触点在不同端面上存在高度差,以达到齿向修形的目的。
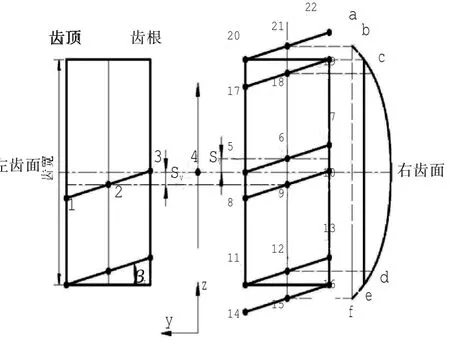
图6 左右齿面展开图
由于接触迹与齿轮端面存在夹角βb,同一条接触迹与齿顶的接触点和齿根的接触点存在高度差2Sv,则同一个齿轮端截面廓形是由不同接触迹共同形成的。
以右齿面为例,齿顶的修形曲线将为ad,齿根的修形曲线将为cf.齿根和齿顶的实际修形曲线将偏离设计的修形曲线。在齿轮上端面,从齿顶到齿根,端面廓形上点的修形量逐渐减小;在齿轮下端面,从齿顶到齿根,端面廓形上各点的修形量逐渐增大。从齿轮上端面到下端面,齿顶到齿根的修形量变化相反,从而造成了齿面扭曲。
2.2 齿面扭曲量的计算
目前,齿面扭曲量的计算并没有统一的公式。由于齿面扭曲最终反映在齿形误差,且齿形误差随着齿向修形曲线连续变化,一般齿轮上下端面处齿形误差的绝对值最大(根据齿面扭曲机理可以判断,上下端面处的齿形误差一个为正值,另一个是负值)。所以,本文以上下端面齿形误差的差值来评定扭曲量。
首先建立齿向鼓形修形曲线各端截面处的齿形误差模型,如图7所示,La为齿顶修形曲线,L为分度圆处修形曲线,Lb为齿根处的修形曲线。

图7 齿形误差模型
图7 中,分度圆处的修形曲线的表达式为:

则齿顶和齿根的修形曲线的表达式分别为:
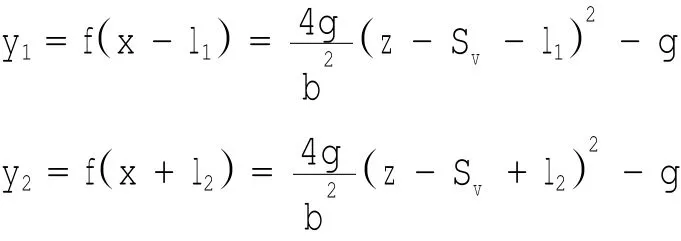
则可以得到任意端面处的齿形误差为:
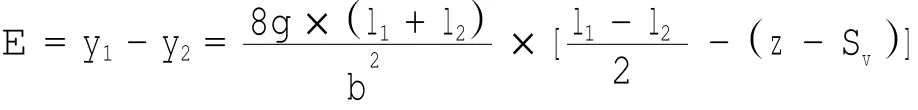
根据本文对齿面扭曲量的定义,齿面扭曲量可
2.3 齿面鼓形修形曲线的优化
由上一节齿面扭曲量的计算公式可以知道,齿面扭曲量与最大修形量g成正比。从齿轮传动考虑,鼓形只需作用在齿宽中部即可使载荷均匀分布在齿宽中部,并不需要全齿宽鼓形。由此,采用二次曲线组合的方式对齿向修形曲线的两端进行优化。图8为齿向修形曲线优化的示意图。
将优化后的齿向修形曲线按齿宽分成三段。优化后的齿向修形曲线的方程为:
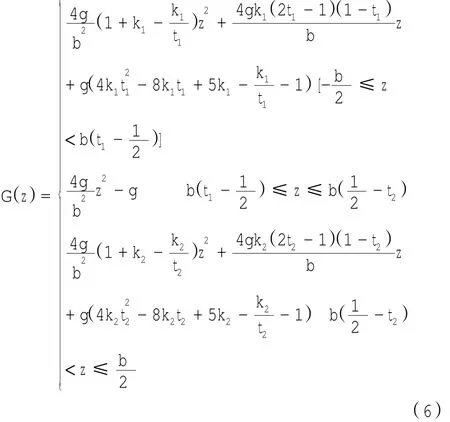
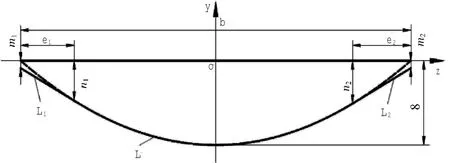
图8 齿向修形曲线优化
式中:t1=e1/b,0 < t1< 0.5;k1=m1/n1,0 < k1< 1;t2=e2/b,0 < t2< 0.5;k2=m2/n2,0 < k2< 1.
由上式可知,通过调整 t1、t2、k1、k2就可以实现不同齿面扭曲修形的设计,控制齿面扭曲在合理范围内。
当t1=t2、k1=k2时,齿面扭曲量为:
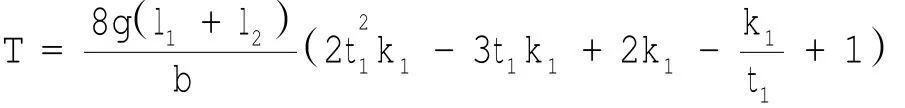
3 计算实例及结果分析
表1是齿轮参数。令该齿轮的齿向鼓形修形的的鼓点在齿宽中点,鼓形修形抛物线系数ρ=0.001 13 mm,最大修形量g=0.02 mm.齿向修形曲线优化参数:t1=t2=0.1,k1=k2=0.09.
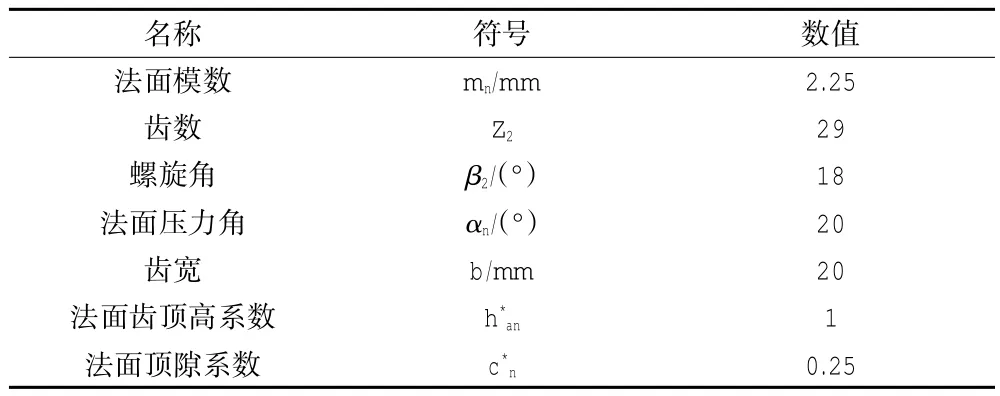
表1 齿轮参数
3.1 齿面扭曲量的计算
根据前面推导的齿面扭曲量的计算公式,计算鼓形修形曲线优化前后齿面的扭曲量。计算结果如下:

从齿向修形曲线优化前后的扭曲量的计算结果可以发现:相较于原本的修形曲线,经过二次曲线组合优化后的修形曲线的扭曲量降低了72%,齿面扭曲量降低效果十分明显。
3.2 齿面接触应力及齿向载荷分布分析
前面已经说明齿向修形的出发点,在此不再赘述。根据齿向修形的目的,分析齿向修形曲线优化前后齿面接触应力以及载荷分布是有必要的。
基于有限元分析法,对平行轴斜齿轮实体副进行网格划分,建立啮合齿面间的接触副,并对齿轮副施加相应约束,得到有限元模型如图9所示。在分析时,认为在任意时刻,齿轮副的啮合运动为准静态过程。
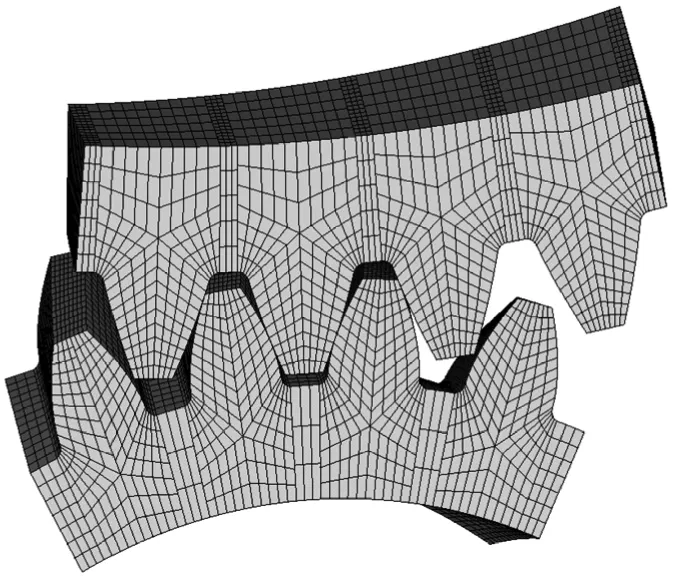
图9 齿轮啮合有限元模型
齿向修行前后齿面的最大接触应力和最大等效应力结果如表2.

表2 齿面应力计算结果
由表2可知,齿向修形后,齿轮副的最大等效应力及最大接触应力均减小。齿向修形曲线优化前后,最大等效应力及最大接触应力几乎没有变化,说明齿向修形曲线的优化对齿面最大等效应力及最大接触应力没有影响。
在齿轮副啮合过程中,提取最长接触线。在该接触线上均匀取点,绘制接触应力曲线,如图10、图11所示。

图10 齿面接触线
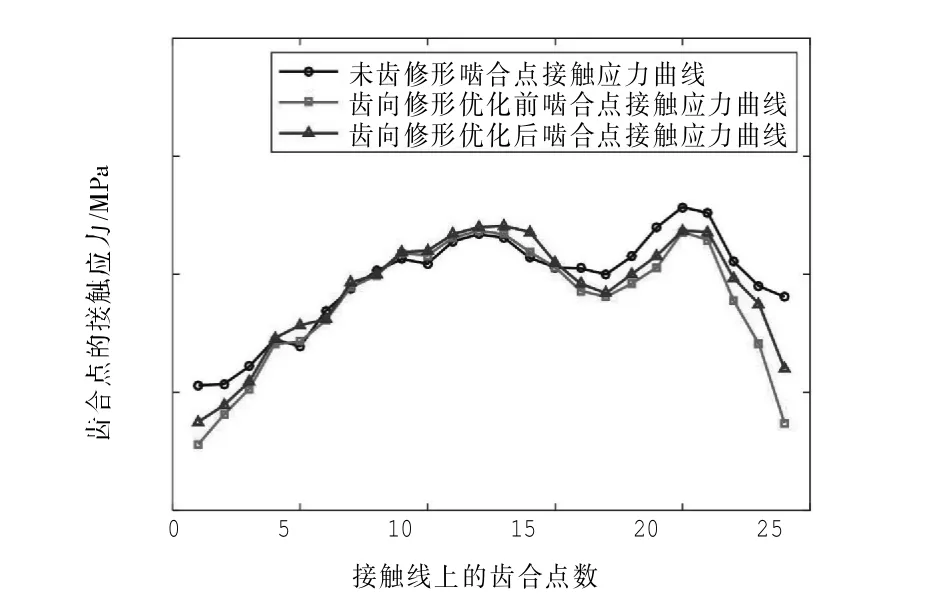
图11 接触线应力曲线
由图10、图11可知,齿向修形齿轮靠近齿轮端面的接触点处的应力较未修形的齿轮小。齿向修形曲线优化后,两端面附近的应力值相对未优化的齿向修形齿轮有所增长,但增加值不大。对载荷的分布影响不大,载荷仍集中分布于齿宽中部。
4 结论
本文计算了齿向修形曲线优化前后齿面扭曲量,分析了齿向修行曲线优化前后齿面接触应力以及齿向载荷的分布,可以得出如下结论:采用二次曲线组合的方法对齿向鼓形修形曲线优化的方法能够将齿面扭曲量控制在理想范围内,并且对齿面接触应力以及齿向载荷的分布没有影响,证明了该方法是可行的。
[1]朱孝录,刘鹄然.齿轮在弯扭偏载下的齿向修形[J].机械,1993(4):15-18
[2]俞 明.斜齿轮的鼓形修整[J].中国纺织大学学报,1990(02):72-78.
[3]马虎森.斜齿轮修形与摩擦激励耦合动力学建模及噪声分析[D].重庆:重庆大学,2015.
[4]F.L.李特文.齿轮几何学与应用理论[M].上海:上海科学技术出版社,2008.
[5]李高敬,孙大琦.蜗杆砂轮磨齿的啮合特征[J].精密制造与自动化,1981(3):18-36.

