不含5-圈和6-圈的平面图的(2,1)-全标号

吕萧,孙磊

(山东师范大学数学与统计学院,山东 济南 250014)

1 引言

频道分配问题是指将电波频率分配给各个传输站,为避免信号干扰,如果两个站点距离非常近,则分配给它们的频率至少要相差2,若两个站点距离较近,但不是非常近,则分配给它们的频率只要不同即可.受此问题启发,Griggs和 Yeh[1]引入了L(2,1)-标号,它的自然推广是L(p,1)-标号[2].Whittesey[3]等人研究了图G的剖分图的L(2,1)-标号.图G的剖分图s1(G)是在图G的每条边上插入一个点得到的图.图s1(G)的L(p,1)-标号对应原图G的一个(p,1)-全标号.图G的k-(p,1)-全标号是对图G的顶点和边的一个标号分配,即存在映射f:V(G)∪E(G)→{0,1,···,k},使得

(1)G中任意相邻两点u,v,有|f(u)−f(v)|≥1;

(2)G中任意相邻两边e,e′,有|f(e)−f(e′)|≥1;

(3)G中任意相关联的点u和边e,有|f(u)−f(e)|≥p.

称这样的一个分配为图G的(p,1)-全标号.(p,1)-全标号的跨度为任意两个标号的最大差值.图G的所有(p,1)-全标号的最小跨度称为(p,1)-全标号数,记作λTp(G).本文中未说明的定义和符号与文献[4]中一致.另外,本文不考虑标号和颜色的区别.

由此可见,图的(p,1)-全标号是加强了条件的全染色问题,即还要求任意一点与其关联边的标号至少相差p.不难看出,图G的(1,1)-全标号恰是图G的全染色,故λT1(G)=χ′′(G)−1,其中χ′′(G) 是全色数.

文献 [5]研究了λTp(G)的上界,证明了λTp(G)≤2∆(G)+p−1.但对最大度较大的图,这个上界并不是紧的.于是,他们给出了猜想:

猜想 1.1[5]λTp(G)≤min{∆(G)+2p−1,2∆(G)+p−1}.

当p=1时,这个猜想即全染色猜想.

文献[5]利用图的最大割证明了

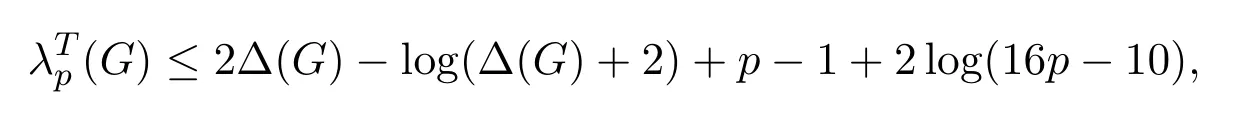
并改进了(2,1)-全标号的某些结果:

若 ∆(G)≥5是奇数,则λT2(G)≤2∆(G)−1;

若 ∆(G)≥2,则λT2(G)≤2∆(G);

若 ∆=2,则λT2(G)=4;

若 ∆(G)≤3,则λT2(G)≤6.

对于平面图,当最大度较小时文献[6]证明了:

若 ∆≤3，围长g≥18,则λT2(G)≤5;

若∆≤4，围长g≥12,则λT2(G)≤7.本文讨论了最大度为6、7、8的图,如果不含5-圈和 6-圈,λT2(G)=2∆−p.

2 主要结果及其证明

定理 2.1若G为连通平面图,∆(G)=p+5,且G不包含5-圈和6-圈,则

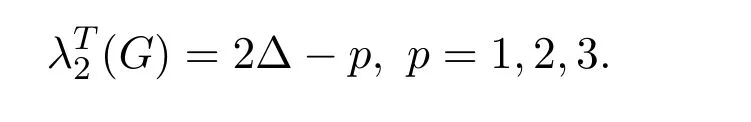
假设G=(V,E)为点数加边数最小的反例,即∆(G)=p+5,且G不包含5-圈和6-圈,而λT2(G)>2∆−p.且G的每一个真子图都能用2∆−p+1种颜色得到(2,1)-全标号.因为G不包含5-圈和6-圈,所以我们有下列观察:

(O1)v是一个4+-点,如果v关联着一个3-面,那么v至少关联2个7+-面;

(O2)每一个k-点(k≥4)至多关联(k-2)个3-面;

(O3)如果一个4-面f与一个4-面相邻,那么f与f′交于一条长为2的路,路上点的度数为∆,2,∆.也就是说如果δ(f)≥3,那么与f相邻的面都是7+面.

G有以下结构性质:

(a)对每条边e=uv∈E,min{d(u),d(v)}≤⌊∆/2⌋,有d(u)+d(v)≥∆+2;

(b)G不含偶圈v1v2v3···v2tv1,使得d(v1)=d(v3)=···=d(v2t−1)=2;

(c)如果最大度点v关联两个2-点v1、v2,那么v1和v2都不关联3-面;

(d)G不包含下图中的构型,分别为图1中的(1)、(2)、(3)、(4).其中黑色点除在下图中的邻点外无其他邻点,在图(1)和(2)中d(v)=∆−1,在图(3)和(4)中d(v)=∆−1.

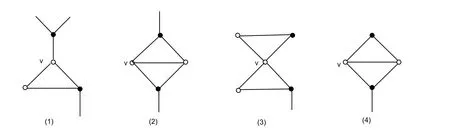
图1 G的构型图

证明(a)假设有一条边uv∈E,使得d(u)≤∆/2,d(u)+d(v)≤∆+1,由G的极小性,G−e可用p+11种颜色得到一个(2,1)-全标号.现擦去点u的颜色.记此时的G的部分(2,1)-全标号为Φ.现在染点u和边uv.对点u,至少有

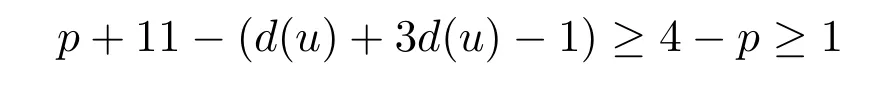
种选择,则可将u染好.对边uv,至少有

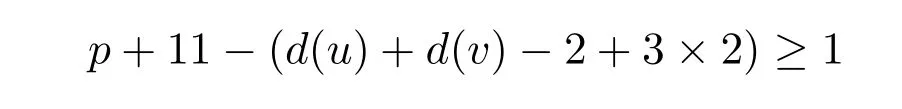
种选择,因此可以将Φ拓展到G上,得到矛盾.

(b)假设G有偶圈

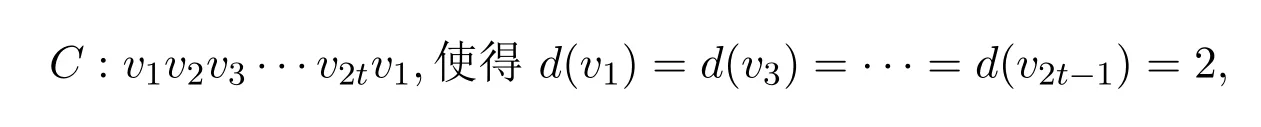
由G的极小性,可用p+11种颜色得到G{v1,v3,···,v2t−1}的一个 (2,1)-全标号,为了染好C上的每条边,对每条边,至少有

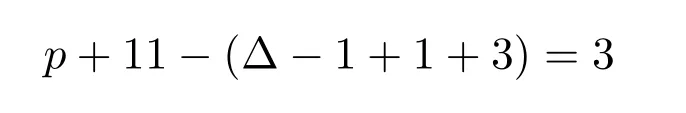
种颜色可选择,现在染好C上的边.对C上的每个2-点,至少有

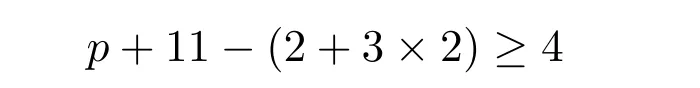
种颜色选择,从而将G−C的(2,1)-全标号拓展到G上,得到矛盾.

(c)设d(v)=6,d(v1)=d(v2)=2,v1关联一个3-面,现由G的极小性,可用p+11种颜色得到G-u1v1的一个(2,1)-全标号.现擦去v1和v2的颜色.将此时的G的部分(2,1)-全标号记作Φ.考虑边u1v1,由u1v1的邻边和关联的点,至少有

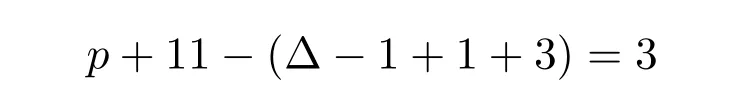
种颜色选择.把边u1v1染好.对于点v1、v2各自至少有

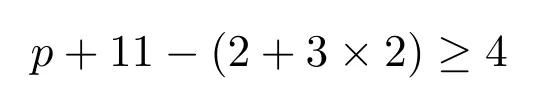
种颜色可供选择.从而将Φ拓展到G上,得到G的p+11种颜色的(2,1)-全标号,得到矛盾.

(d)情形 1设d(v)=∆−1,d(u)=d(w)=3.由G的极小性,可用p+11种颜色得到H=G{uv,wv}的一个(2,1)-全标号,擦去点u和w的颜色.记此时的G的部分(2,1)-全标号为Φ.记AΦ(x)为x的可用颜色集,x∈V(G)∪E(G).下文中都用此记号来记可用颜色集.现在先来染点w和边vw.对点w,至少有p+11−(3+2×3)≥3种颜色可供选择.对边wv,至少有

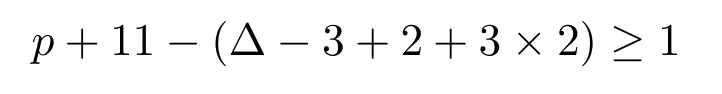
种颜色选择.现在将点w和边wv染好.

下面讨论点u和边uv.对点u至少有

种颜色可供选择,对边uv至少有

种颜色可供选择.选择α∈AΦ(u)来染点u.如果

那么可以选择γ∈AΦ(uv){α−1,α,α+1}染好边uv;否则

那么可以选择AΦ(u)中除α之外的两种颜色之一β去染u.因为

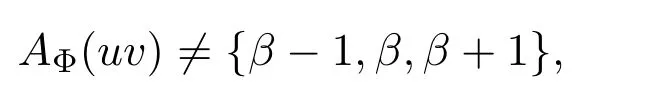
可选择γ′∈AΦ(uv){β−1,β,β+1}来染边uv.从而将Φ拓展到了G上,得到p+11种颜色的G的(2,1)-全标号,矛盾.

情形 2设d(v)=∆−1,d(u)=d(w)=3.由G的极小性,可用p+11种颜色得到H=G{uv,wv}的一个(2,1)-全标号,擦去点u和w的颜色.记此时的G的部分(2,1)-全标号为Φ.现在先来染点w和边vw.对点w,至少有

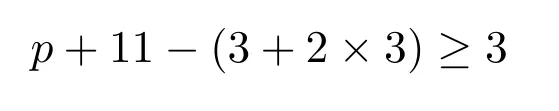
种颜色可供选择.对边wv,至少有

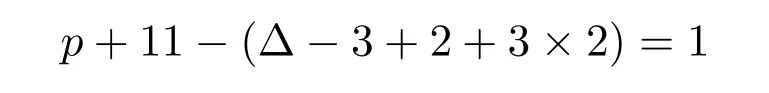
种颜色可供选择.现在将点w和边wv染好.

下面讨论点u和边uv.对点u至少有

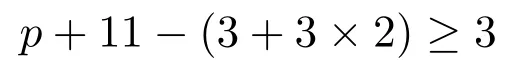
种颜色可供选择,对边uv至少有

种颜色可供选择.选择α∈AΦ(u)来染点u.如果

那么可以选择γ∈AΦ(uv){α−1,α,α+1}染好边uv;否则

那么可以选择且β∈AΦ(u)去染u.因为

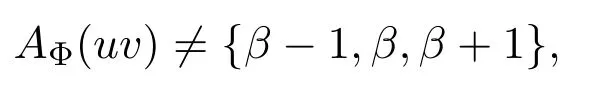
故可选择γ′∈AΦ(uv){β−1,β,β+1}来染边uv.从而得到Φ在G上的拓展,即p+11种颜色的G的(2,1)-全标号,得到矛盾.

情形3设d(v)=∆,d(u)=3d(w)=2.由G的极小性,可用p+11种颜色得到H=G−uv的一个(2,1)-全标号,擦去点u和w的颜色.用Φ记此时的G的部分(2,1)-全标号.现在先来染点w.对点w,至少有

种颜色可供选择,将点w染好.现在讨论点u和边uv,对点u,至少有

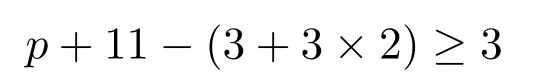
种颜色可供选择,对边uv至少有

种颜色可供选择.选择α∈AΦ(uv)来染边uv.如果

那么可以选择γ∈AΦ(u){α−1,α,α+1}染好u;否则

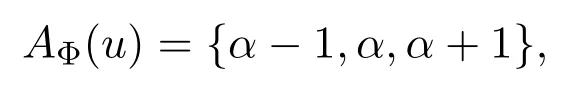
那么可以选择β∈AΦ(uv){α}去染uv.又因为

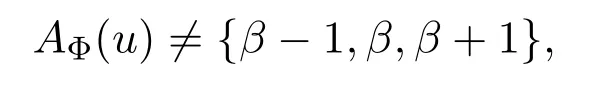
可选择γ′∈AΦ(u){β−1,β,β+1}来染点u.从而得到 Φ在G上的拓展,即p+11种颜色的G的(2,1)-全标号,矛盾.

情形4设d(v)=∆,d(u)=3d(w)=2.由G的极小性,可用p+11种颜色得到H=G−uv的一个(2,1)-全标号,擦去点u和w的颜色.用Φ记此时的G的部分(2,1)-全标号.现在先来染点w.对点w,至少有

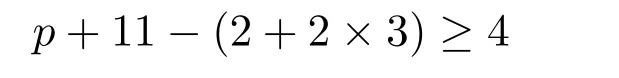
种颜色可供选择,将点w染好.现在讨论点u和边uv,对点u,至少有

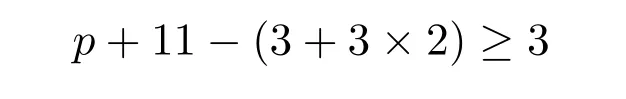
种颜色选择.对边uv至少有

种颜色可供选择.选择α∈AΦ(uv)来染边uv.如果

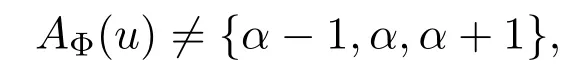
那么可以选择γ∈AΦ(u){α−1,α,α+1}染好u;否则

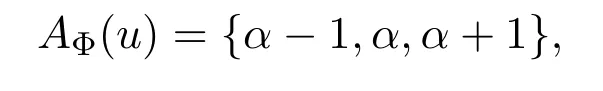
那么可以选择β∈AΦ(uv){α}去染uv.又因为

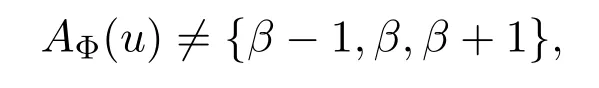
故可选择γ′∈AΦ(u){β−1,β,β+1}来染点u.从而得到 Φ在G上的拓展,即p+11种颜色的G的(2,1)-全标号,矛盾.

G是平面图,由欧拉公式|V(G)|−|E(G)|+|F(G)|=2,有

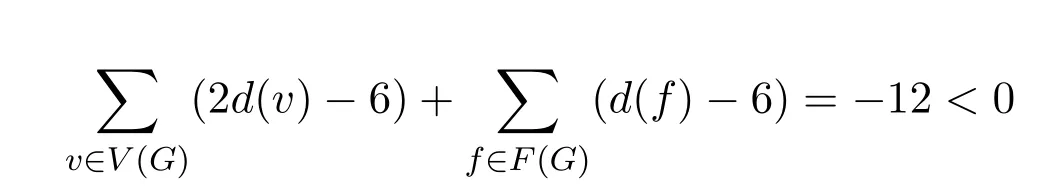
定义原始权值,∀x∈V(G),w(x)=2d(x)−6.∀x∈F(G),w(x)=d(x)−6.由上式知权值总和为−12.下面根据权值转移规则,则给每个x∈V∪F分配新权值w′(x).权值规则不会影响总和.所以

下面来证∀x∈V∪F,w′(x)≥0得到矛盾.权值转移规则如下:

(R1)每个2-点从它的每个邻点接收1.

(R2)每个4+-点给每个关联的4-面1.

(R3)每个4-点给每个关联的3-面1.

(R4)每个5+-点给每个关联的3-面如果δ(f)≤3;否则,给 1.

现在验证∀x∈V∪F,w′(x)≥0:

设f为G中任意一个面.

如果d(f)≥7,显然w′(f)=w(f)≥0.

如果d(f)=4,显然w(f)=−2.由结构性质(a),f至少关联2个4+-点,

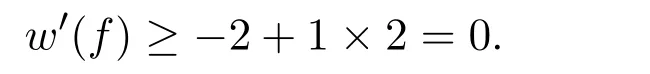
如果d(f)=3,显然w(f)=−3.由结构性质(a),f关联3个4+-点或至少关联2个5+-点,

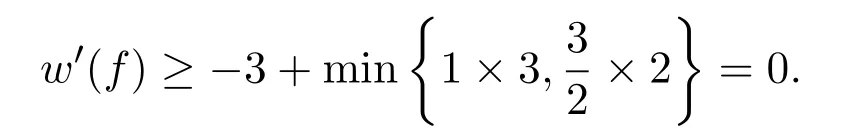
设v为G中任意一个顶点.

如果d(v)=2,w′(v)=w(v)+1×2=0.

如果d(v)=3,w′(v)=w(v)=0.

如果d(v)=4,w(v)=2,由结构性质(a),v的邻居都是4+-点,由观察(O1)和(O3),v至多关联 2个 7−-面,w′(v)≥2−2×1=0.

如果d(v)=∆−1=p+4(p=1,2,3),初始权值w(v)=2p+2,而且由结构性质(a),v的邻居都是3+-点(a).若v关联一个3-面f,由观察(O1),那么v至少关联两个7+-面.如果δ(f)=3,那么由结构性质(d),n3(v)=1,即至多有一个3-面从v处接收

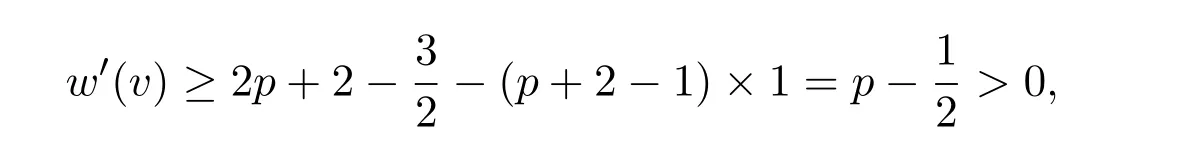
否则v给关联的面p+2,w′(v)=2p+2−(p+2)=p>0;若v关联的都是 4+-面,因为G不含5-和6-圈,所以v至多关联p+1个4-面,

如果

初始权值w(v)=2p,由结构性质(a),v的邻居都是4+-点,因为G不含5-圈和6-圈，v至多关联p+1个 7−-面,w′(v)≥2p−(p+1)=p−1>0.

如果

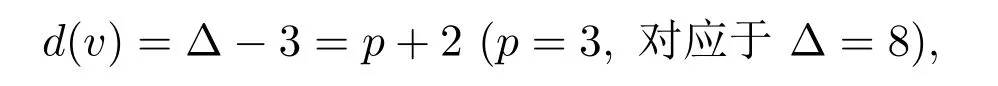
初始权值w(v)=2p−2,由结构性质 (a),v的邻居都是 5+-点,v至多关联p个 7−-面,w′(v)≥2p−2−p=p−2>0.

如果

若v关联的邻居都是3+-点,由观察(O1),v至多关联(∆−2)=p+3个从v点接收的3-面,否则考虑与v关联的2-点的个数n2(v).

如果n2(v)=1,由观察 (O1)和(O3),v至多关联 (∆−2)=p+3个4−-面,由性质 (d)其中至多有(p+1)个从v点接收的3-面,

如果n2(v)=2,由观察(O3)和结构性质(b)(c),p=1(∆=6)时,v会关联2个3-面,至多p个4-面或1个3-面,至多(p+1)个4-面或不关联3-面,至多(p+3)个4-面,此时

p=2(∆=7)时,v会关联3个 3-面,至多(p−1)个4-面或2个 3-面,至多p个4-面或1个 3-面,至多(p+1)个4-面或不关联 3-面,至多(p+3)个4-面,

p=3(∆=8)时,v会至多关联4个3-面,不关联4-面或关联3个3-面,至多(p−1)个4-面或2个3-面,至多p个4-面或1个3-面,至多(p+1)个4-面或不关联3-面,至多(p+3)个 4-面,

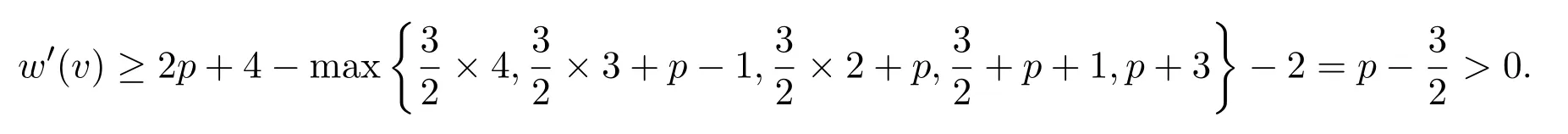
如果n2(v)=3,由观察 (O3)和结构性质(b)(c),p=1(∆=6)时,v会关联 2个 3-面,至多p−1个4-面或1个 3-面,至多p个4-面或不关联3-面,至多(p+2)个 4-面,

p=2(∆=7)时,情况与p=1(∆=6)时相同,此时

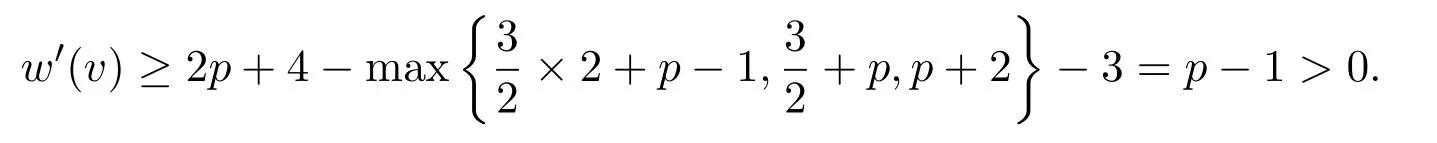
p=3(∆=8)时,v会关联3个 3-面,至多 (p−2)个 4-面或 2个 3-面,至多p−1个4-面或 1个3-面,至多p个4-面或不关联3-面,至多(p+2)个4-面;

如果n2(v)=4,由观察(O3)和结构性质(b)(c),p=1(∆=6)时,v会关联1个3-面,至多p−1个4-面或不关联3-面,至多(p+1)个 4-面;

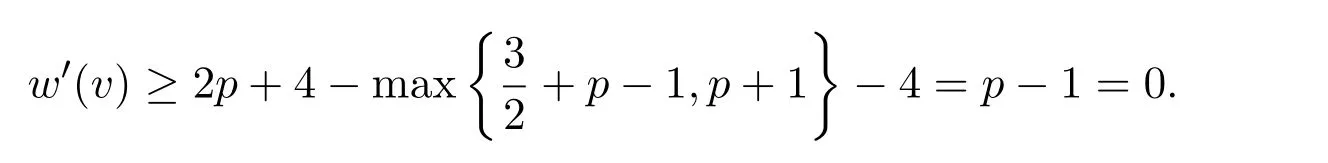
p=2(∆=7)时情况与p=1(∆=6)时相同,此时

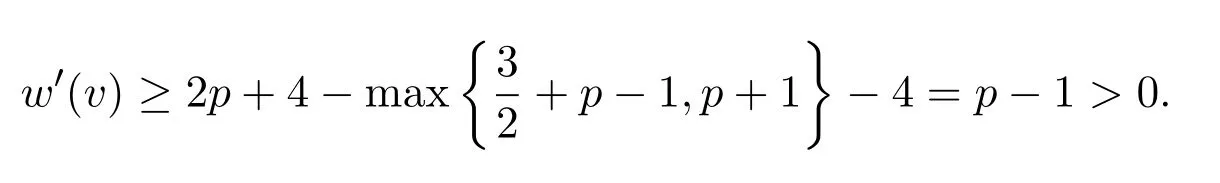
p=3(∆=8)时,v会关联 2个3-面,至多p−2个4-面或 1个3-面,至多p−1个4-面或不关联 3-面,至多(p+1)个4-面,从而

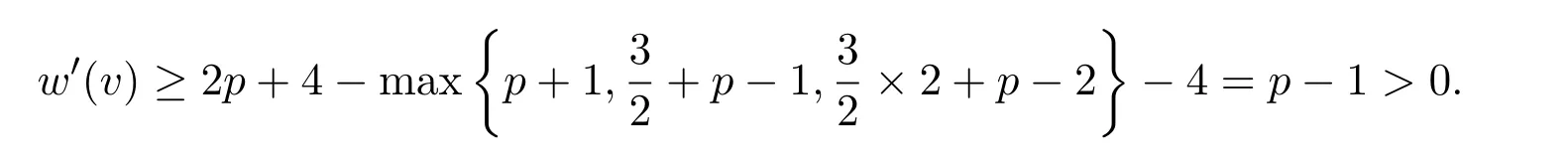
如果n2(v)=5,由观察(O3)和结构性质(b)(c),p=1(∆=6)时,v不关联3-面,至多p个 4-面;此时

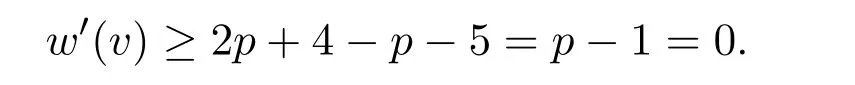
p=2(∆=7)时,v会关联1个3-面,至多p−2个4-面或不关联3-面,至多p个4-面,此时

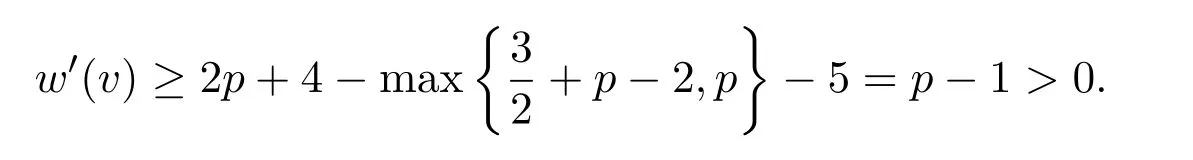
p=3(∆=8)时,v会关联 2个3-面,至多p−3个4-面或 1个3-面,至多p−2个4-面或不关联 3-面,至多p个4-面.此时

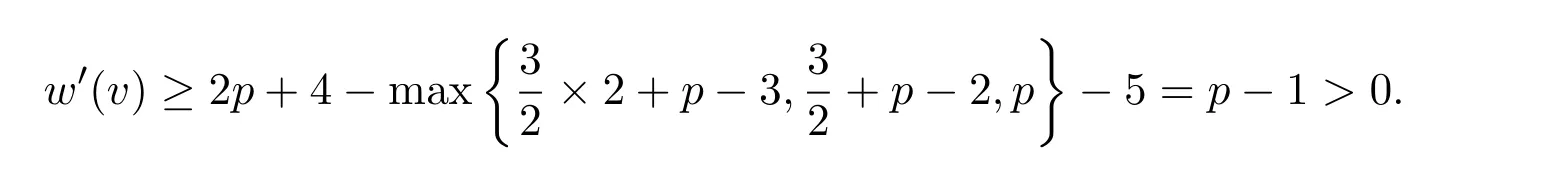
如果n2(v)=6,由观察(O3)和结构性质(b)(c),p=1(∆=6)时,v既不关联3-面也不关联4-面,此时

p=2(∆=7)时,v不关联 3-面,至多 (p−1)个 4-面,此时

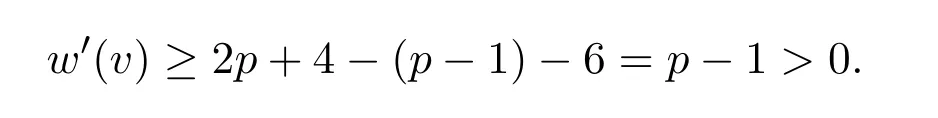
p=3(∆=8)时,v会关联1个 3-面,至多(p−3)个4-面或不关联3-面,至多 (p−1)个4-面,此时

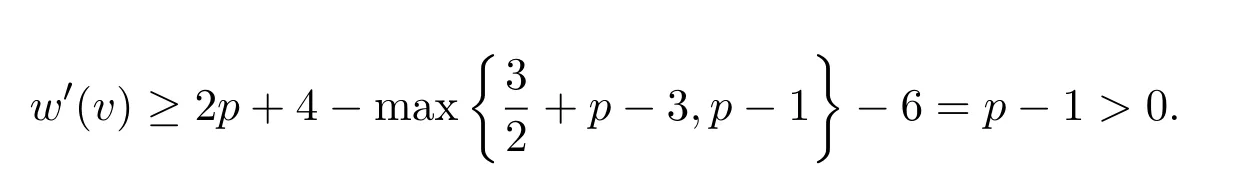
特别地,∆=7、8时,情况如下:

如果n2(v)=7,由观察(O3)和结构性质(b)(c),p=2(∆=7)时,v既不关联3-面也不关联4-面,此时

p=3(∆=8)时,v不关联3-面,至多(p−2)个4-面.此时

如果n2(v)=8,p=3即∆=8时,v既不关联3-面也不关联4-面.此时

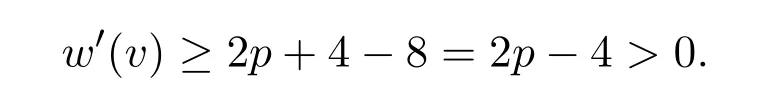
于是移值后,在任何一种情况下,对每个元素x∈V(G)∪F(G),有w′(x)≥0,所有点数值和这与矛盾,从而完成定理1的证明.

[1]Griggs J R,Yeh R K.Labeling graphs with a condition at distance two[J].SIAM J.Discrete Math.,1992,5:586-595.

[2]Chang G J,Ke W T,Kuo D,et al.On L(d,1)-labeling of graphs[J].Discrete Math.,2000,220:57-66.

[3]Whittlesey M A,Georges J R,Mauro D W.On theλ-number ofQnand related graphs[J].SIAM J.Discrete Math.,1995,8:449-506.

[4]Yu Y,Zhang X,Wang G,et al.(2,1)-Total labeling of planar graphs with large maximum degree[J].Computer Science,2011,26(1):53-59.

[5]Havet F,Yu M L.(p,1)-Total labeling of graphs[J].Discrete Mathematics,2008,308(4):496-513.

[6]Sun Lei,Li Haiying.(2,1)-Total labeling of planar graphs with large girth and low degree[J].Ars Combinatoria,2011,100:65-72.