近拟常曲率黎曼流形中的伪脐子流形

刘金梦,宋卫东

(安徽师范大学数学与统计学院,安徽 芜湖 241003)

1 引言

近拟常曲率黎曼流形是Gazi[1]等人在拟常曲率流形概念的基础上提出来的,其黎曼曲率张量R满足:

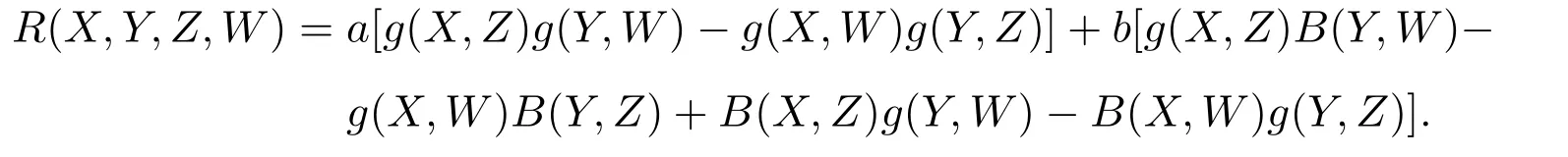
其中a,b为流形上的光滑函数,g为Nn+p的黎曼度量,B为2-阶非零对称共变张量场.

显然,当b=0时,近拟常曲率黎曼流形即为实空间形式.

关于近拟常曲率黎曼流形,近年来已有不少研究结果[2-4]．本文用活动标架法对伪脐子流形进行研究,证明了:

定理 1.1设Mn是近拟常曲率空间Nn+p中紧致无边伪脐子流形,则有如下积分不等式:

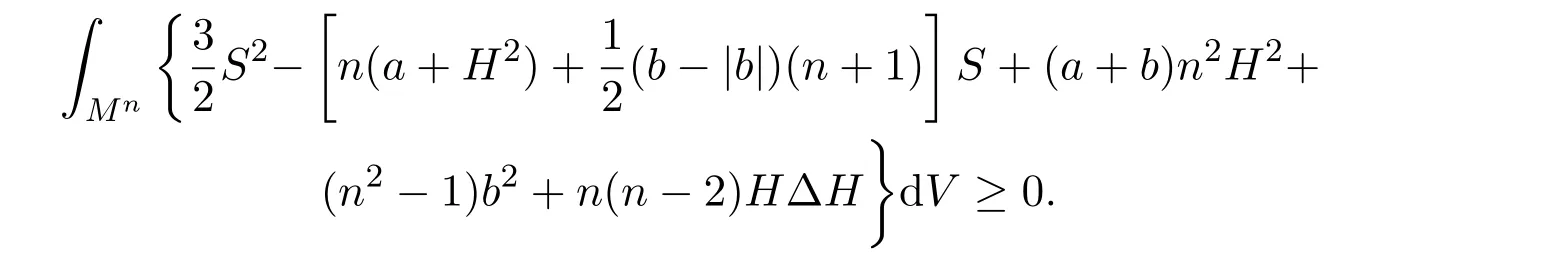
其中,S为Mn的第二基本形式模长平方;H为Mn的平均曲率.

推论 1.1设Mn是近拟常曲率空间Nn+p中具有平行平均曲率伪脐子流形,则下列积分不等式成立:

其中,S为Mn的第二基本形式模长平方;H为Mn的平均曲率.

推论 1.2设Mn是近拟常曲率空间Nn+p中紧致无边全实极小子流形,若第二基本形式模长平方S满足则Mn为全实全测地子流形.

2 预备知识

约定各类指标的取值范围

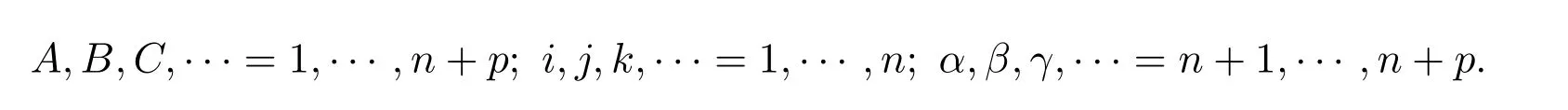
设Mn是n+p维完备的黎曼流形Nn+p中n维子流形．在Nn+p上选取局部规范正交标架场

使得限制于Mn,{e1,···,en+p}与Mn相切．在此标架场下,以Nn+p表示黎曼流形,若其曲率张量取为如下形式:

则称Nn+p为近拟常曲率空间.其中,g为Nn+p的黎曼度量,a,b为Nn+p上的光滑函数,{fAB}为单位向量函数.

以{ωA}表示{eA}的对偶标架场,{ωAB}是Nn+p的联络形式,则Nn+p的结构方程为:

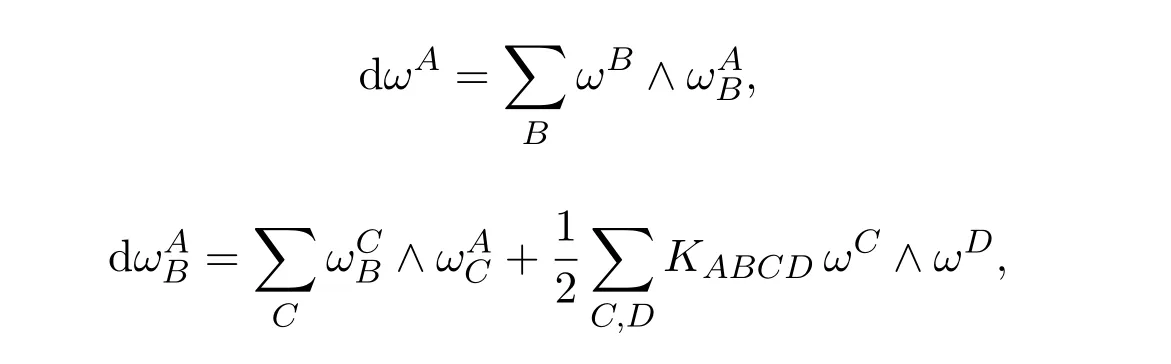
其中

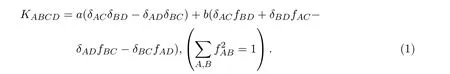
将{ωA},{ωAB}限制在Mn,有

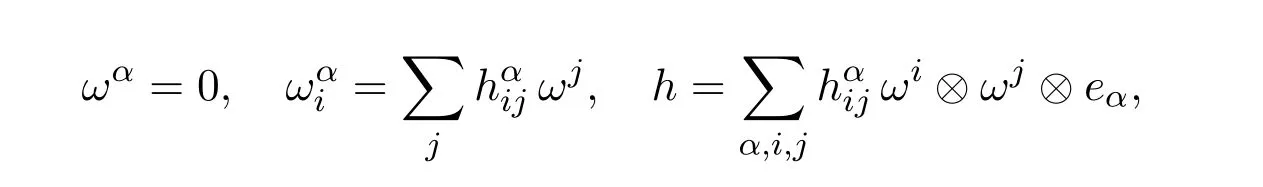
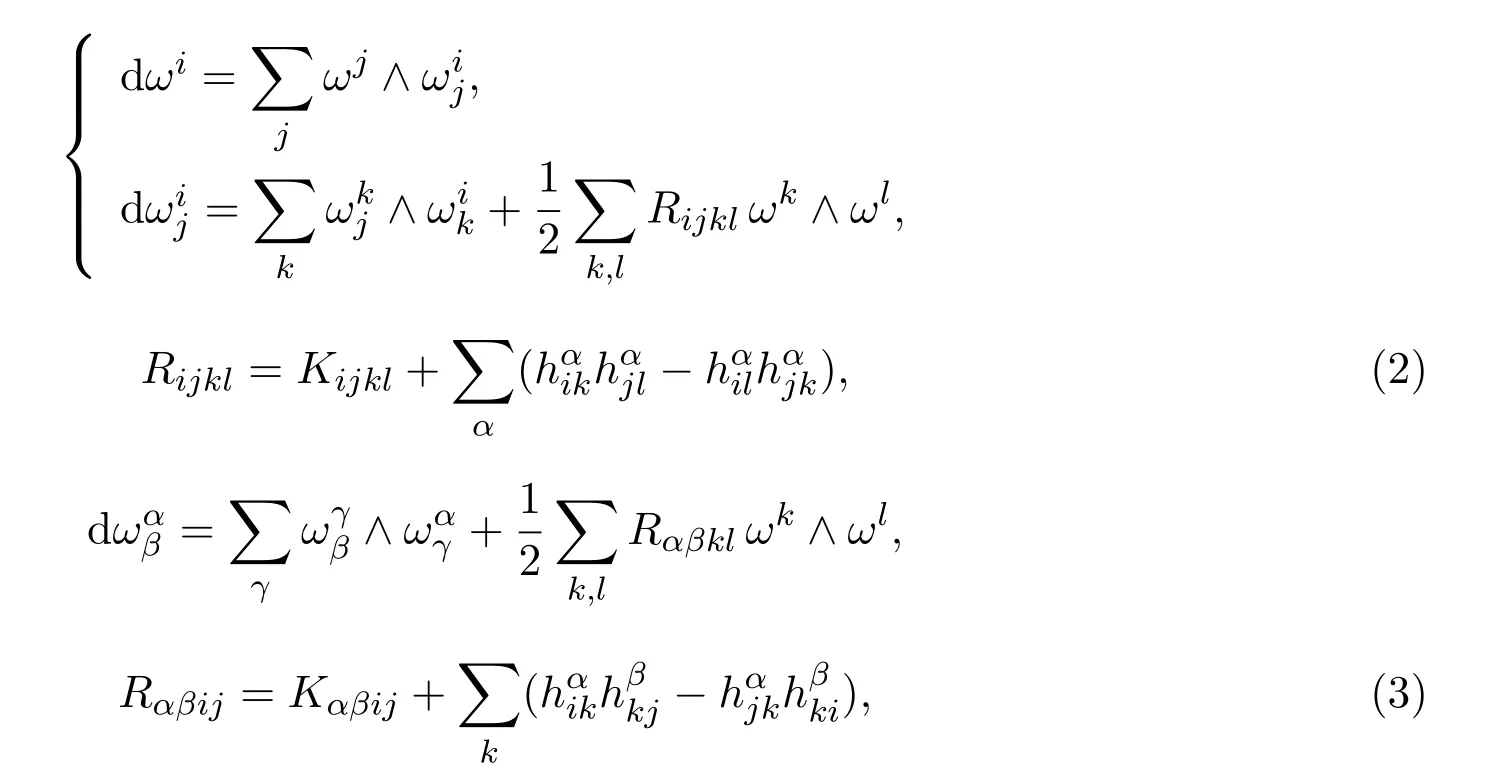
其中h,Rijkl,Rαβij分别为Mn的第二基本形式,Riemann曲率张量场和法曲率张量场R⊥关于{eA}的分量,设ζ为Mn的平均曲率向量场,即

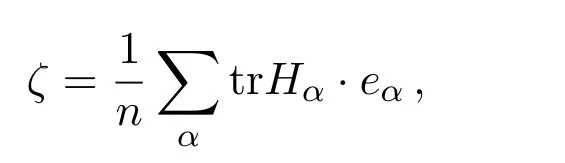
其中trHα为矩阵的迹,称H=|ζ|为Mn的平均曲率．记

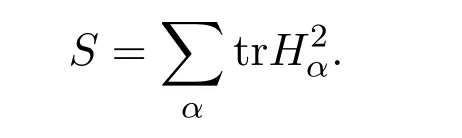
引理 2.1[6]设Mn是n+p维黎曼流形Nn+p中的任一子流形,则

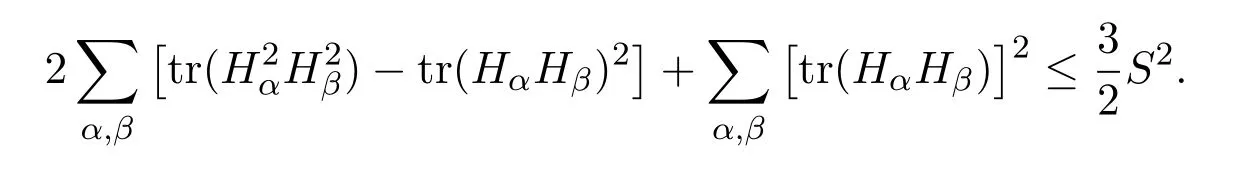
引理 2.2[7]设Mn是任意n+p维黎曼流形Nn+p中n维紧致伪脐子流形,则

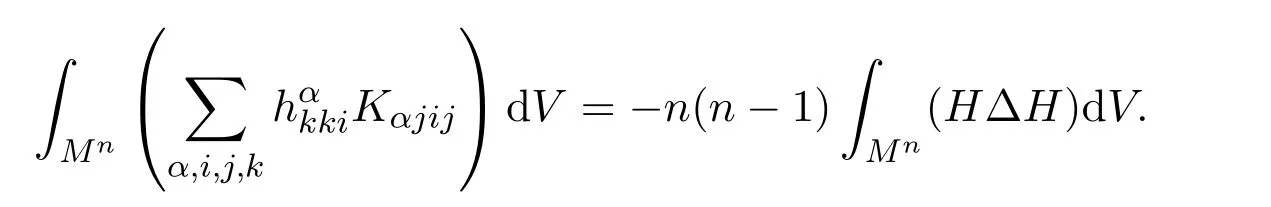
定义的共变微分为:

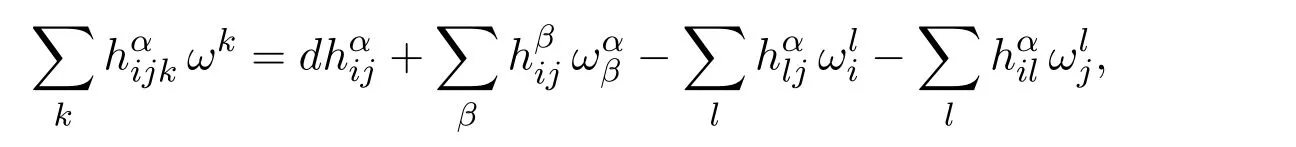
则[5]

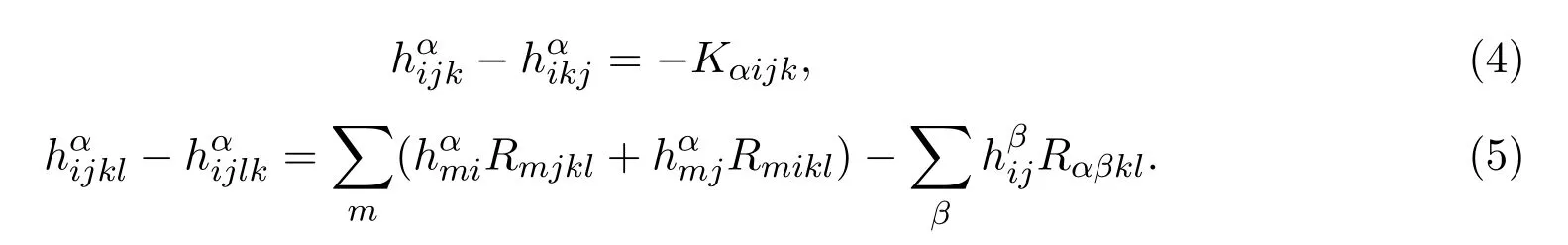
由 (1)式,易见,

由 (5)式,的Laplacian为

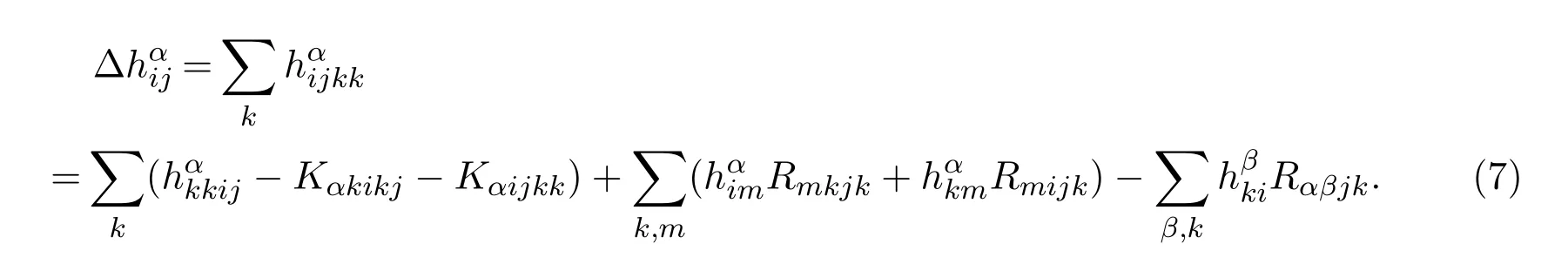
又由(1)-(3),(7)式,经计算后得到

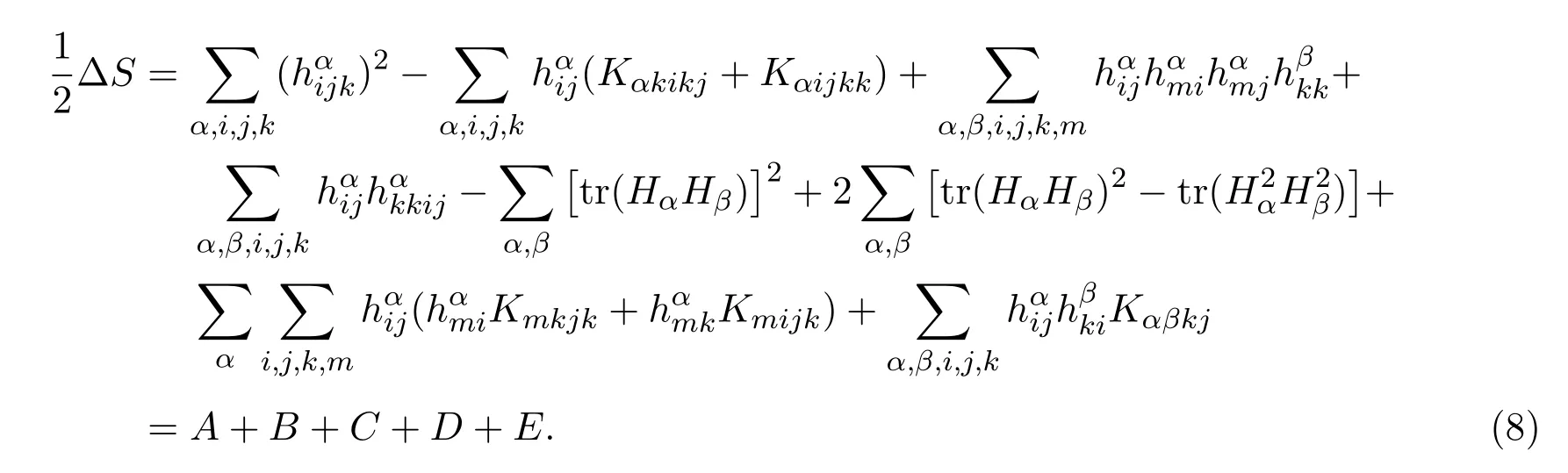
其中

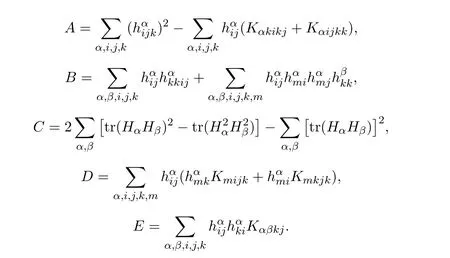
3 定理的证明

设Mn上有H>0,选取结合Mn是紧致伪脐的,有

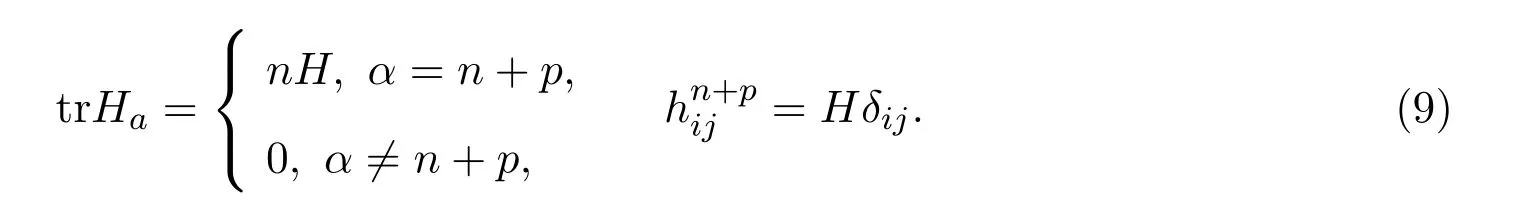
下面估计A,先定义[8]

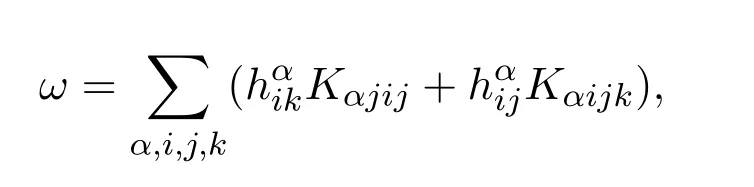
则ω的散度为:

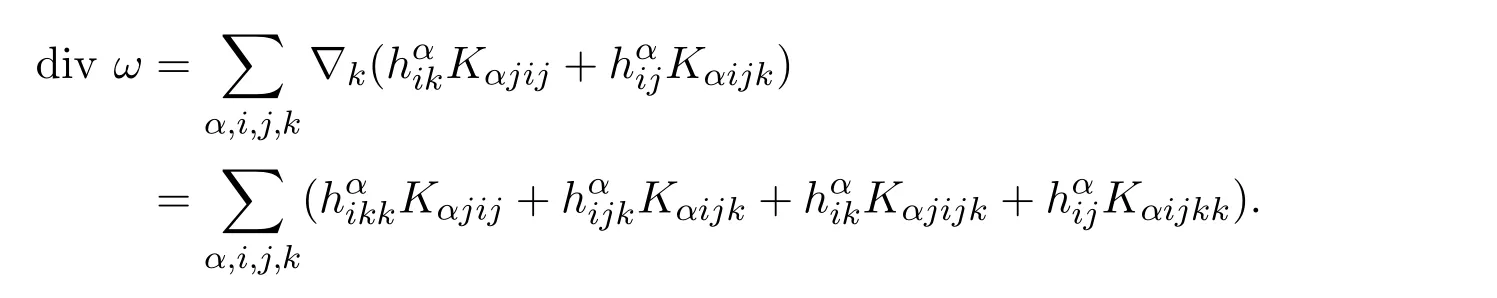
再由(1),(4)式,经简单计算有

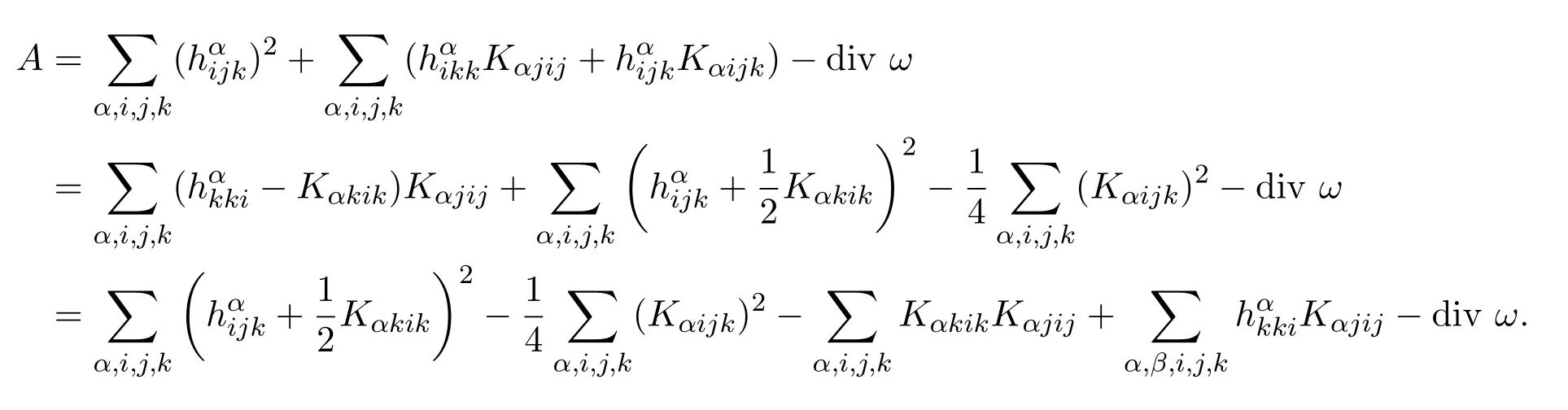
由于

利用(4)式,得到

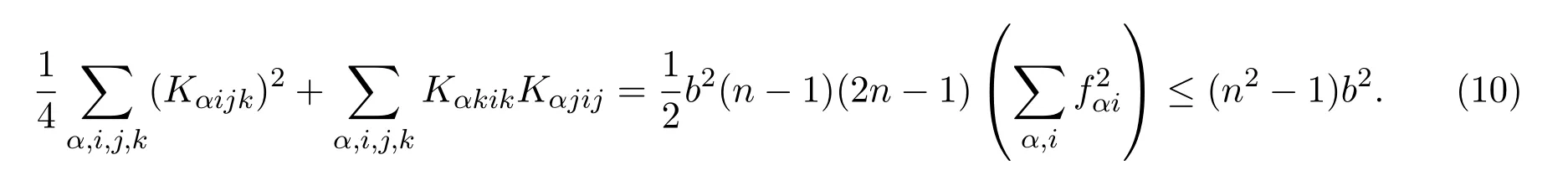
由 (10)式,引理2.2及Green散度定理,得

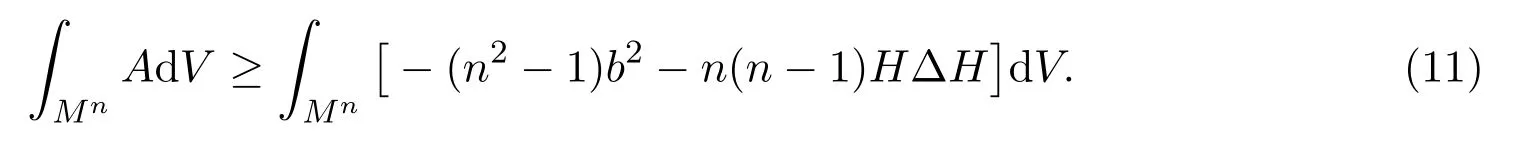
由 (9)式,得

由(13),(14)式,计算后得

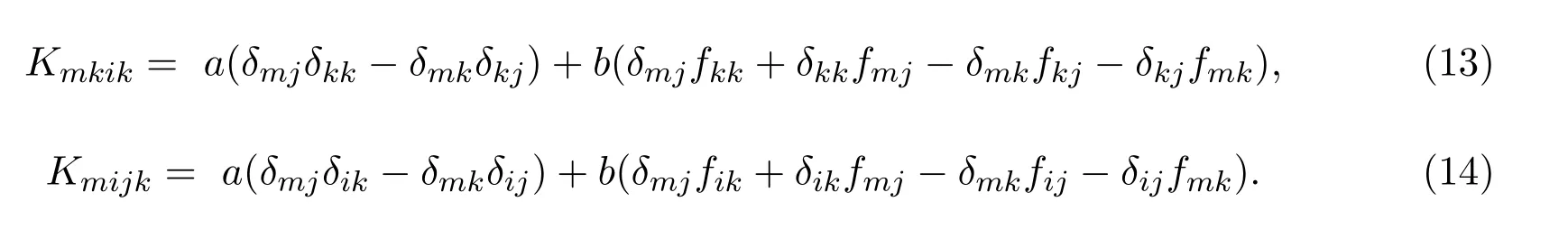
根据(9)式,有

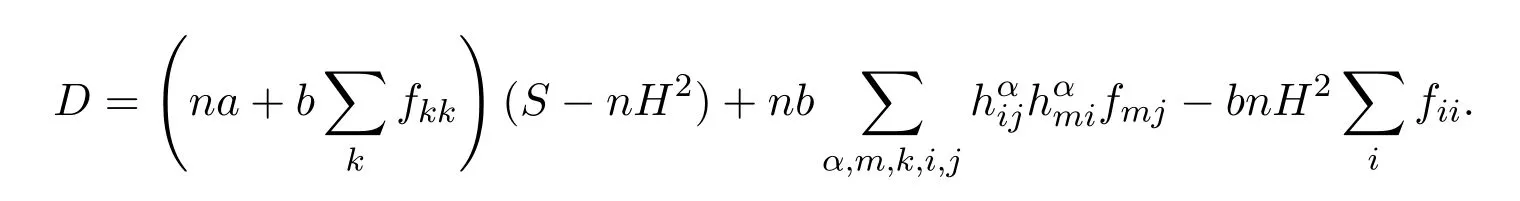
(I)当b≥0时,由则

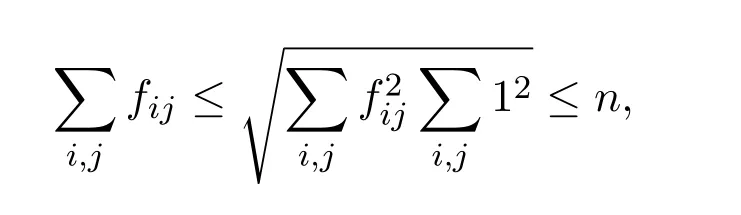
所以

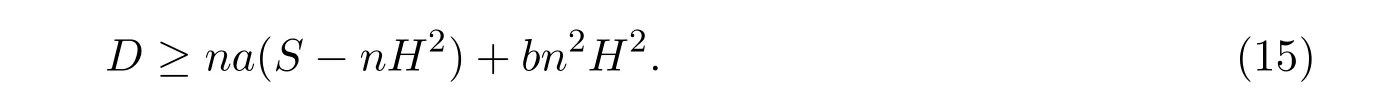
(II)当b<0时,由Schwartz不等式,得

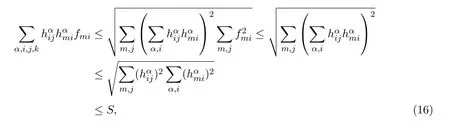
所以

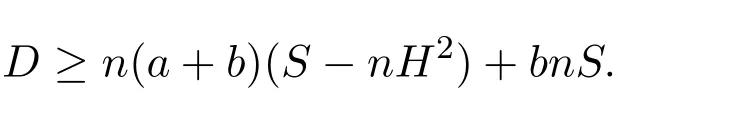
综合(15),(16)式

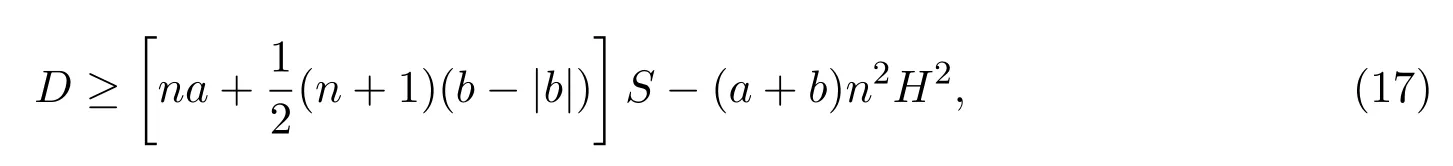
另外,由(6)式知

结合(11),(12),(16),(18)式及引理2.1,有

定理得证.

由于Mn具有平行平均曲率,即

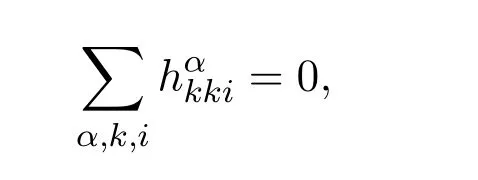
所以推论1.1可直接由定理1.1得到.

由于Mn是近拟常曲率空间Nn+p中紧致无边全实极小子流形,即

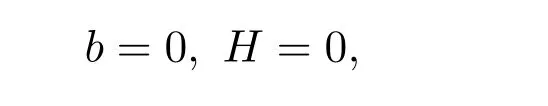
则定理1.1中的积分不等式可以化为

由此可直接得出推论1.2.

[1]Gazi A K,De U C.On the existence of nearly quasi-Einstein manifold[J].Novi.Sad.J.Math.,2009,39(2):111-117.

[2]Zhang Pan.Remarks on Chen′s inequalities for submanifolds of a riemannian manifold of nearly quasiconstant curvature[J].Vietnarm J.Math.,2015,43:557-569.

[3]Zhang Pan,Pan Xuling,Zhang Liang.Inequalities for submanifolds of a riemannian manifold of nearly quasiconstant curvature with a semi-symmetric non-metric connection[J].Uni´on Math.argentian,2015,56(2):1-19.

[4]苏曼,张量.近拟常曲率空间中双重卷积子流形的不等式[J].吉林大学学报(理学版),2016,54(5):952-959.

[5]Chern S S,Do Carmo M,Kobayashi S.Minimal Submanifolds of a Sphere with Second Fundamental Form of Constant Length[M].Berlin:Spring-Verlag,1978.

[6]Li Anmin,Li Jimin.An intrinsic rigidity theorem for minimal submanifolds in sphere[J].Arch.Math.,1992,58(6):582-594.

[7]宋卫东,朱岩.拟复射影空间中的全实伪脐子流形[J].吉林大学学报(理学版),2012,50(4):673-677.

[8]宋卫东,储昭昉.拟常曲率黎曼流形中的伪脐子流形[J].吉林大学学报(理学版),2004,42(3):361-365.