代数法：易想难算 几何法：多思少算

☉江苏省启东市折桂中学 赵春风

在数学问题解决过程中，我们时常会发现有的问题既可以从代数的角度进行解答，又可以从几何的角度进行解答，而两种方法中有时各有千秋，有时平分秋色.本文呈现两则案例，分别从代数和几何的角度给出解答，并进行简单的分析，同时对案例2进行简单改编，不当之处，敬请指正.

案例1（根据2016年烟台卷第25题第（3）问改编）如图1，点A的坐标为（2，6），点C的坐标为（4，3），过点A、C的直线分别与x轴的正半轴、y轴的正半轴交于点H、G，P是直线AC上的任意一点，设其横坐标为m，过点P向x轴和y轴分别作垂线，垂足分别为M和N，连接MN，求线段MN的最小值并给出此时m的值.

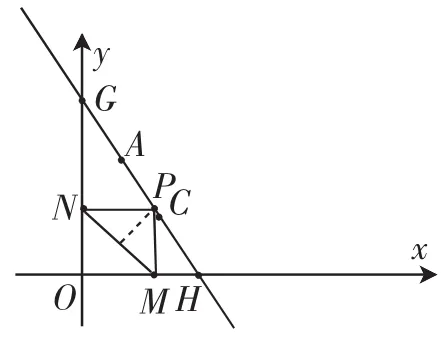
图1

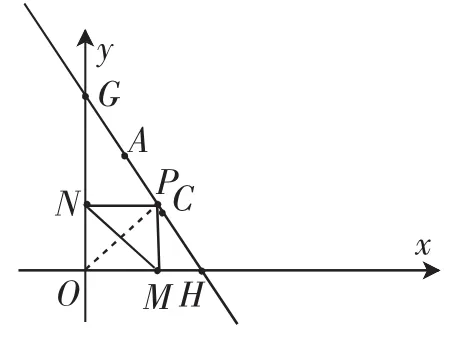
图2

方法1：（代数法）由待定系数法得过点A、C的直线的方程为于是可设点P的坐标为），进而可得点M的坐标为（m，0），点N的坐标为），所以，所以当时，MN2取到最小值，即MN的最小值为

方法2：（几何法）由待定系数法得过点A、C的直线的方程为所以OH=6，OG=9.

由题意得MN=OP，显然当OP⊥HG时（如图2），线段OP的长度最小，即此时所以

所以MN的最小值为，此时

方法1从代数的角度给出，可以看出思路非常自然，然而计算过程比较复杂，在考试过程中可能很难得到正确的答案.方法2从几何的角度给出解答，整个求解过程计算简单，利用了点与线之间，垂线段最短，以及“面积相等算两次”的基本方法，但是有一定的思维含量，特别是学生可能很难求出m的值，因为学生很难与相似三角形或锐角三角函数产生联系，如果从这个角度看的话就不如方法1了，方法1可以说是一箭双雕，在得到MN的最小值的同时也得到了m的值.

案例2如图3，△ABC是边长为4的等边三角形，D是边BC上的任意一点，连接AD，作线段AD的垂直平分线交边AC于点N，求线段CN的最大值.

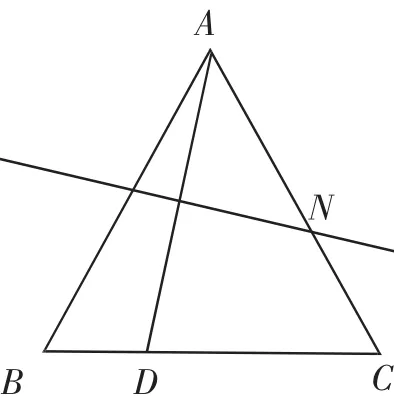
图3

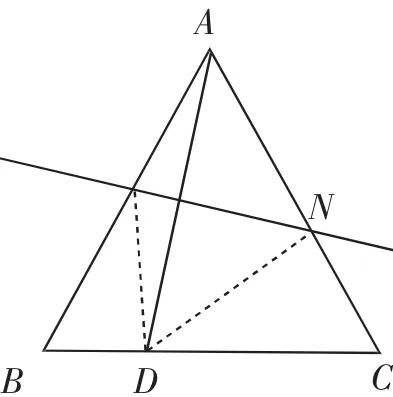
图4

方法1：（代数法）如图4，连接MD、ND，则△BMD∽△CDN.

设BD=x（0≤x≤4），CN=y，则△BMD的周长为4+x，△CDN的周长为8－x，根据相似三角形的性质（相似三角形的相似比等于周长比）得，解得

令 t=4+x， 则 4 ≤t≤8， 所 以，即当，也就是说当时，y取到最大值，所以线段CN的最大值为

方法2：（几何法）如图5，连接ND，过点N作NP⊥BC，垂足为P.

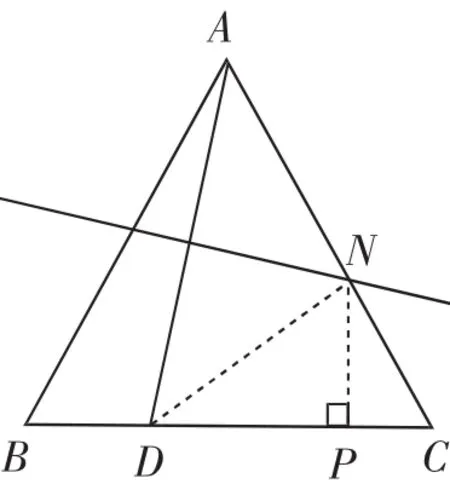
图5

于是当DN与NP重合（DN=NP）时，线段CN取到最大值

方法1中学生比较容易发现图形中的相似三角形（一线三等角），此时学生很容易陷入误区，仅仅考虑到“相似三角形的对应边成比例”，而忽略了“相似三角形的周长比等于相似比”这一重要的性质，导致学生不能得到正确的关系式.即使有的学生可以得到正确的关系式，也不可能求出最大值，这里用到了高中阶段的均值不等式，需要注意满足“一正、二定、三相等”，如果从这个角度考虑的话这应该不是命题人的本意.方法2从几何的角度出发，具有一定的技巧性，应用“直角三角形的斜边大于直角边”这一事实进行求解，也很难想到.说实话，这种方法对于学生而言应该是很难想到的，大多数的老师应该也在其中（笔者是在用几何画板演示过程中发现当DN与NP重合时，CN取到最大值，才有了上述的方法2）.

下面针对上述问题对案例2进行简单改编（题干不变）：

（1）如图4，连接MD、ND，证明△BMD∽△CDN；

（2）设BD=x，CN=y，请给出y与x的函数关系式并写出自变量x的取值范围；

（3）设（2）中得到的函数在自变量取值范围内的最大值为m，请直接写出点D从点B移动到点C的过程中，点N在边AC上移动路径的长度共为多少？（用含m的代数式进行表示）

参考答案：（1）（2）略.（3）2m－2.

上述试题的改编灵感来自于下述两题：

题1：（2017年东营卷第24题）如图6，在等腰三角形ABC中，∠BAC=120°，AB=AC=2，D是边BC上的一点（不与点B、C重合），在AC上取一点E，使∠ADE=30°.

（1）求证：△ABD∽△DCE；

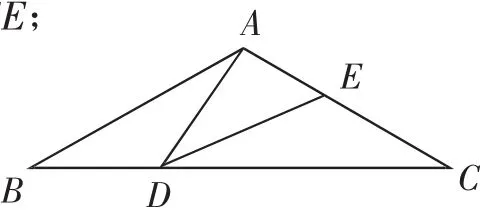
图6

（2）设 BD=x，AE=y，写出y与x的函数关系式，并写出自变量x的取值范围；

（3）略.

题2：（2017年嘉兴卷第16题）如图7，一副含30°和45°角的三角板ABC和DEF叠合在一起，边BC与EF重合，BC=EF=12cm，G为边BC（EF）的中点，边FD与AB相交于点H，此时线段BH的长是.现将三角板DEF绕点G按顺时针方向旋转，如图8，在∠CGF从0°到60°的变化过程中，点H相应移动的路径长共为（结果保留根号）

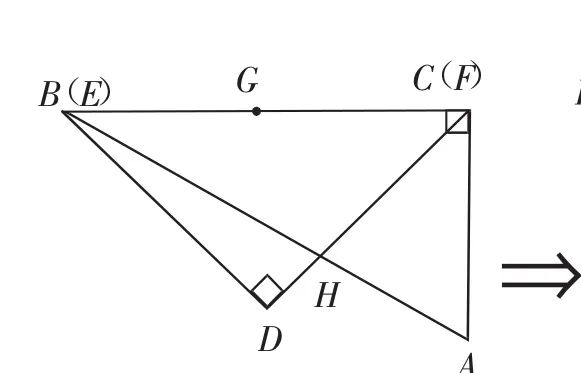
图7

图8

通过上面的介绍可以看出，代数法需要通过构造函数关系，进而将问题解决；几何法则需要用到垂线段最短（案例1），直角三角形中斜边大于直角边（案例2）.当然见的最多的可能是两点之间线段最短（将军饮马问题），以及圆上动点与圆外定点之间距离的最大值和最小值等问题.可以说两种方法各有千秋，甚至平分秋色；但是，笔者认为“代数法：易想难算，几何法：多思少算”.H