抛物线“牵手”几何图形为哪般

☉江苏省南京市竹山中学 黄秀旺

二次函数是初中数学的重点内容之一，每年全国各地的中考试卷中都会出现以二次函数为背景的解答题，其综合性较强，难度较高.其中，有些问题借助抛物线上一个点或两个点，讨论三角形或四边形的形状或图形之间的关系，此时可以“拿掉”抛物线，似有“假二次函数问题”之嫌；还有一类问题，将抛物线的“轴对称性”与几何图形（轴对称图形）的“轴对称性”相结合，其构思巧妙又不失自然与合理，将函数图像与几何图形因轴对称之缘而“牵手”，凸显抛物线的轴对称性，渗透数形结合、几何直观的数学思想方法.解决此类问题就是要将图像的对称性与图形的对称性结合起来，从对称性的角度进行推理，发现新结论.

一、好题赏析

例1如图1，已知抛物线y=ax2+bx+c经过A（1，0）、B（4，0）、C（0，3）三点.

（1）求抛物线的解析式.

（2）如图1，在抛物线的对称轴上是否存在点P，使得PA+PC最小？若存在，求出PA+PC的最小值；若不存在，请说明理由.

分析：（1）设抛物线的解析式为y=a（x－1）（x－4），把C（0，3）代入得a·（－1）·（－4）=3，解得，所以抛物线的解析式为，即

图1

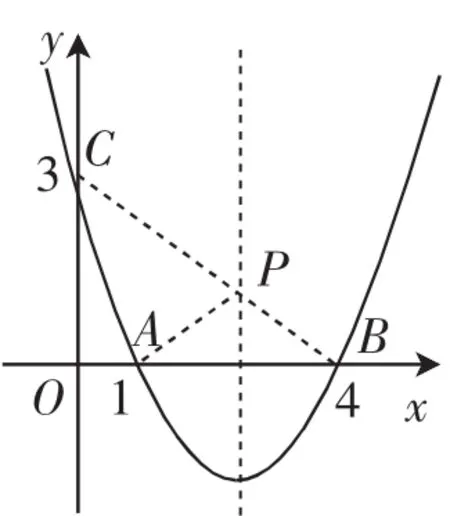
图2

解：（1）略.

（2）存在.因为A（1，0）、B（4，0），所以抛物线的对称轴为直线

连接BC交直线于点P，如图2，则PA=PB，PA+PC=PC+PB=BC，此时PC+PA最短，因为所以PA+PC的最小值为5.

拓展1：如图2，在抛物线的对称轴上是否存在点P，使得四边形PAOC的周长最小？若存在，求出四边形PAOC周长的最小值；若不存在，请说明理由.

拓展2：如图2，在抛物线的对称轴上是否存在点P，使得抛物线的对称轴平分∠CPB？若存在，求出点P的坐标；若不存在，请说明理由.

点评：例1中的第（2）小题是典型的“将军饮马”问题，通常我们需要作点A关于一条直线的对称点；拓展1求四边形PAOC周长的最小值，其本质仍是PA+PC取最小值；拓展2通过问题转化，需作点B关于直线的对称点（即点A），连接CA并延长，直线CA与直线的交点即为点P.从以上分析发现，问题解决需运用抛物线的对称性，由于点A与点B关于直线对称，所以无需作图就可得到点A（或点B）的对称点，以上拓展问题凸显了抛物线的对称性.

例2某水渠的横截面呈抛物线形，水面的宽为AB（单位：m）.现以AB所在直线为x轴，以抛物线的对称轴为y轴建立如图3所示的平面直角坐标系，设坐标原点为O.已知AB=8m.设抛物线的解析式为y=ax2－4.

（1）求a的值；

（2）C（－1，n）是抛物线上一点，点C关于原点O的对称点为点D，连接CB、BD、DC，求△BCD的面积.

分析：（1）因为AB=8，由抛物线的对称性可知OB=4，所以B（4，0），0=16a－4，所以（.2）把C点坐标代入解析式，求得n的值，再根据D、C关于原点对称求出点D坐标，然后根据求出面积即可.

图3

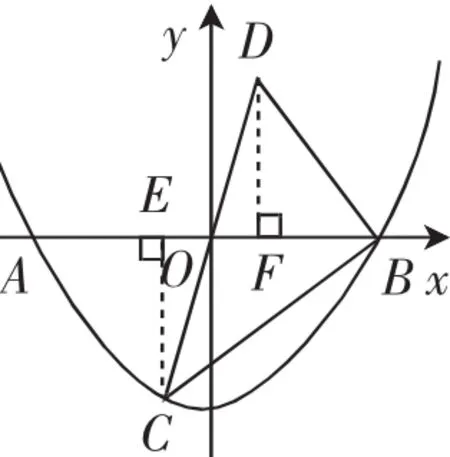
图4

解：（1）略.

（2）过点C作CE⊥AB于点E，过点D作DF⊥AB于点F，如图4所示.

由（1）知

令x=-1，得，所以

因为点C关于原点的对称点为点D，所以

所以

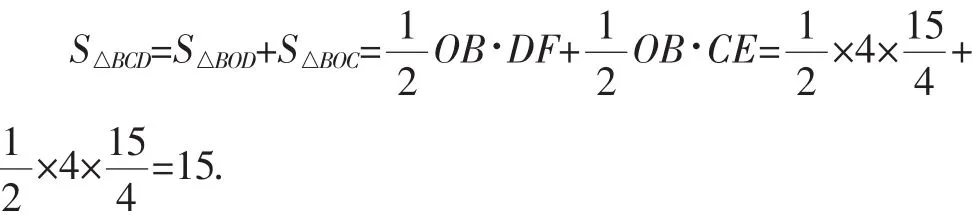
所以△BCD的面积为15m2.

拓展1：求四边形ACBD的面积.

拓展2：如果C是抛物线上一个动点，点C关于原点O的对称点为点D，连接AC、CB、BD、DA，那么是否存在四边形ACBD是矩形？若存在，求出点C的坐标；若不存在，请说明理由.

拓展3：对于抛物线y=ax2+c（a≠0），它与x轴交于点A、B，C是抛物线上一个动点，点C关于原点O的对称点为点D，连接AC、CB、BD、DA，是否存在四边形ACBD是正方形？请探究a与c之间的数量关系.

拓展4：对于抛物线y=ax2+bx+c（a≠0），它与x轴交于点A、B，C是抛物线上一个动点，点C关于点）的对称点为点D，连接AC、CB、BD、DA，是否存在四边形ACBD是正方形？请探究a、b、c之间满足的数量关系.

点评：“点C关于原点O的对称点为点D”为题目给出的条件，结合抛物线的对称性，点A与点B关于y轴所在直线对称，由此可以推测点A与点B关于原点O对称，从而可以判定四边形ACBD是平行四边形.接下来的拓展1、拓展2、拓展3进一步讨论四边形ACBD的面积，以及它是否可以为矩形、正方形，特别是探究正方形时，将充分关注抛物线的对称性与正方形的对称性，并且它们有一条对称轴是相同的.

例3如图5，直线y=－3x+3与x轴、y轴分别交于点A、B，抛物线y=a（x－2）2+k经过点A、B，并与x轴交于另一点C，其顶点为P.

（1）求a，k的值；

（2）在抛物线及其对称轴上分别取点M、N，使以A，C，M，N为顶点的四边形为正方形，求此正方形的边长.

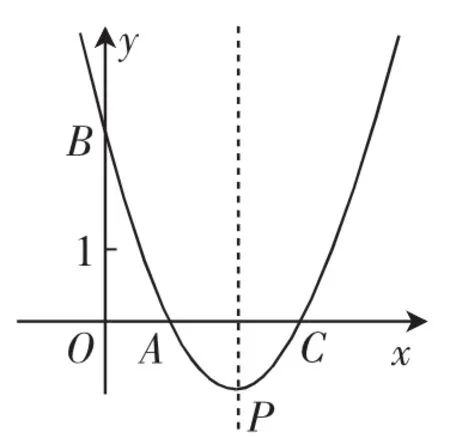
图5

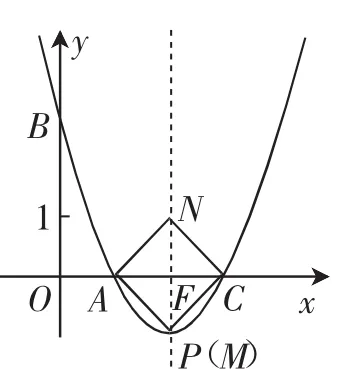
图6

分析：（1）因为直线y=－3x+3与x轴、y轴分别交于点A、B，所以A（1，0），B（0，3）.又抛物线y=a（x－2）2+k经过点A（1，0），B（0，3），所以解得即a，k的值分别为1，－1.（2）如图6，当点N在对称轴上时，由NC与AC不垂直，得出AC为正方形的对角线，根据抛物线的对称性及正方形的性质，得到M点与顶点P（2，－1）重合，N点为点P关于x轴的对称点，此时，MF=NF=AF=CF=1，且AC⊥MN，则四边形AMCN为正方形.在Rt△AFN中，根据勾股定理即可求出正方形的边长.

解：（1）略.

（2）当点N在对称轴上时，NC与AC不垂直.所以AC应为正方形的对角线.又对称轴x=2是AC的中垂线，所以M点与顶点P（2，－1）重合，N点为点P关于x轴的对称点，其坐标为（2，1）.此时MF=NF=AF=CF=1，且AC⊥MN，所以四边形AMCN为正方形.

在Rt△AFN中，即正方形的边长为

拓展1：是否存在⊙P，使得⊙P经过点A、C，且与y轴相切？若存在，请求出点P的坐标；若不存在，请说明理由.

点评：例3紧扣正方形的性质，从点A与点C之间的关系，以及AC的长，结合抛物线的对称性推出M点与N点之间的关系及其位置；拓展1将圆的对称性与抛物线的对称性结合起来，从“⊙P经过点A、C”结合圆的对称性可以判断圆心P在直线x=2上.

例4如图7，已知二次函数y=x2－2x－1的图像的顶点为A.二次函数y=ax2+bx的图像与x轴交于原点O及另一点C，它的顶点B在函数y=x2－2x－1的图像的对称轴上.

（1）求点A与点C的坐标；

（2）当四边形AOBC为菱形时，求函数y=ax2+bx的关系式.

分析：（1）因为y=x2－2x－1=（x－1）2－2，所以顶点A的坐标为（1，－2）.因为二次函数y=ax2+bx的图像与x轴交于原点O及另一点C，它的顶点B在函数y=x2－2x－1的图像的对称轴上，所以二次函数y=ax2+bx的对称轴为直线x=1，所以点C和点O关于直线x=1对称，所以点C的坐标为（2，0）.（2）因为四边形AOBC是菱形，根据菱形的性质，可以得出点O和点C关于直线AB对称，点B和点A关于直线OC对称，因此可求出点B的坐标.根据二次函数y=ax2+bx的图像经过点B（1，2），C（2，0），将B，C代入解析式得出a、b的值，进而得出其解析式.

解：（1）略.

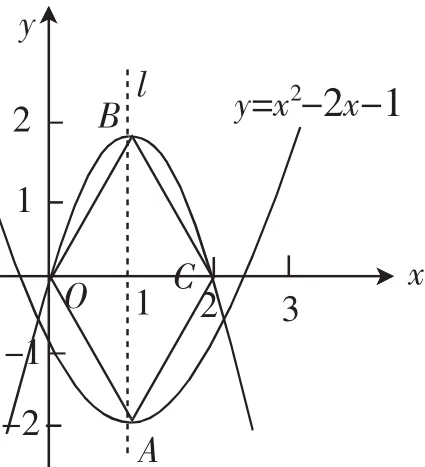
图7

（2）因为四边形AOBC是菱形，所以点B和点A关于直线OC对称，因此点B的坐标为（1，2）.

因为二次函数y=ax2+bx的图像经过点B（1，2），C（2，0），所以解得所以y=－2x2+4x.

拓展1：当四边形AOBC的面积为6时，求函数y=ax2+bx的关系式.

拓展2：当以点A、O、B、C为顶点构成的四边形的面积为6时，求函数y=ax2+bx的关系式.

拓展3：观察拓展1和拓展2所求得的函数关系式，并结合其图像的位置，请你再写一个与它们有共同特点的函数关系式.

点评：第（2）小题，从二次函数y=ax2+bx的图像性质可知，点O与点C关于直线AB对称，而当四边形AOBC是菱形时，点O与点C也是关于直线AB对称的，所以函数y=ax2+bx的对称轴就是菱形AOBC的一条对角线所在的直线，进而确定点B的位置；拓展1与拓展2都关注点O与点C关于直线AB对称，从而过点A、B的直线垂直OC，而四边形的面积可以改变，但是抛物线y=ax2+bx经过点O、C则是不变的，解题的关键是确定点B的坐标.

二、感悟与归纳

等腰三角形、菱形、正方形、等腰梯形、圆等都是轴对称图形，而抛物线也具有轴对称性，因此，有些试题可以将抛物线与几何图形结合起来，一方面，通过抛物线的对称性容易获得图像上一个点的对称点，为进一步探究几何图形的形状提供条件；另一方面，几何图形的对称性也可以确定相关线段的长度，进而确定图像上点的坐标，所以抛物线“牵手”几何图形为哪般呢，原因在于它们都具有轴对称性！ H