刮膜蒸发过程中软测量模型的ADHDP学习控制

李 慧 , 常化鹏, 董 博, 秦 伟

(1.长春工业大学 电气与电子工程学院， 吉林 长春 130012;2.长春工业大学 汽车工程研究院， 吉林 长春 130012;3.吉林大学 通信工程学院， 吉林 长春 130012)

0 引 言

随着人们对天然物质的青睐以及全球回归自然潮流的兴起，特别是中药现代化、国际化进程的迫近，分子蒸馏技术在高沸点、热敏性天然物质的分离方面得到了迅速发展[1]。但是分子蒸馏过程强耦合、非线性和大滞后的特点很难对其进行优化控制，1978年Brosillow.C B提出可以通过过程中容易直接测量的变量(控制变量)建立软测量数学模型推导出所需的主导变量(状态变量)[2]，并在化工过程中得到了广泛应用。刮膜式分子蒸馏作为一种应用最广的分子蒸馏方式，利用高速转动的刮板在蒸发面上形成并更新既均匀又薄的液膜，加强了蒸发效果，但也使蒸发过程变得更加复杂，虽然Cvengroš等[3-4]利用Navier-Stokes方程、Boltzmann方程和热量衡算关系式对气相中的重力下的液膜流动的传热传质过程进行了建模，Mckenna等[5]也通过将流体的物性参数以及设备的结构参数联系起来建立了液膜非稳态的数学模型，但是蒸发过程机理的复杂性以及随着工况以及环境的改变发生变化,预测性能也大大降低，普适性较差，软测量神经网络模型非线性拟合能力强，且不需要对象的先验知识，对处理复杂过程的建模问题具有独到的优势[2]，但是存在预测精度差、收敛速度慢、稳定性差等问题，基于此，Huang提出了序贯极限学习机[6-7](Onlin Sequential Extreme Learning Machine， OS-ELM)，其具有以下特点：用于实现学习算法的训练数据是顺序的，可以是一个基于时间的数据，也可以是固定长度的批量数据，还可以是变化长度的批量数据,任何时刻只对新来的数据进行学习,一旦对新的数据学习结束，就丢弃掉这些数据,不需要先验知识来确定这种算法需要多少训练样本。大大提高了软测量模型的可靠性和预测精度。

文中通过建立基于数据的OS-ELM软测量模型，并采用ADHDP对各影响蒸发效率的控制变量进行学习寻优，得到了最优的状态变量，实现了对刮膜式分子蒸馏系统的优化控制。

1 刮膜蒸发过程的软测量模型

1.1 刮膜蒸发过程

刮膜式分子蒸馏器的旋转轴和安装在旋转轴上的辊筒共同组成刮膜器，物料沿壁面从顶部进入，蒸发液膜在刮板的旋转作用下不断更新，当旋转轴转动时，辊筒在离心力的作用下紧贴在蒸发器表面，物料在辊筒与蒸发面共同的作用下在蒸发器表面形成一层液膜。头波与之前形成的液膜不断地进行混合更新，这种不断混合更新有利于液膜内浓度分布均匀，增加了传热和传质效果[8-9]。刮膜式分子蒸馏器的结构如图1所示。

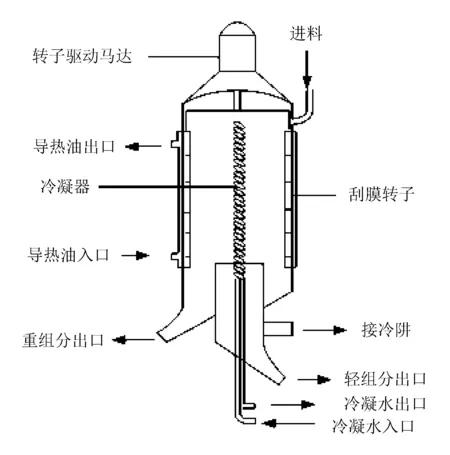
图1 刮膜式分子蒸馏器的内部结构

在蒸发工艺工程中，提纯物纯度是一个很重要的指标，在刮膜蒸发过程稳定的情况下，与状态变量纯度存在强耦合关系，并可以直接获得的控制变量主要有以下几个[8-12]：

1)进料速度。进料速度直接影响着液膜的更新及其薄厚,以及在蒸发面上停留的时间，合适的进料速率能使蒸发面积得到充分利用，有效提高蒸发速率。

2)刮膜电机转速。刮膜电机的转速决定了液膜更新速度的快慢以及液体的平均停留时间，进而影响到状态量纯度。

3)真空度。合理增大系统的真空度能够减少分子间的碰撞，降低轻分子因碰撞而发生的氧化可能性，保证了被提纯物的原有属性。

4)蒸发温度。如果蒸发温度过高，液膜就容易发生氧化、聚合等现象，而温度低的情况下会降低分子活跃度,影响蒸发速率与分离效率，还会影响产品的纯度。

1.2 OS-ELM软测量模型

OS-ELM原理：

一个标准的具有N个任意不同样本(xj,tj)的单隐层前馈网络，其中xj=[xj1,xj2,…,xjn]T∈Rn，tj=[tj1,tj2,…,tjm]T∈Rm，激活函数为g(·),假设具有L个隐层神经元，可记为：

(1)

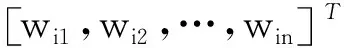
βi——隐层第i个神经元和输出层神经元之间的输出权值;

bi——隐层第i个神经元的阈值;

wi·xj——wi和xj的内积。

单隐层神经网络学习的目标是使输出的误差最小,可以表示为:

(2)

即存在wi、xj和bi使得：

(3)

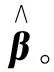
i=1,2,…,L

这等价于最小化损失函数

(4)

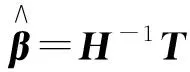
H-1=(HTH-1)HT

(5)

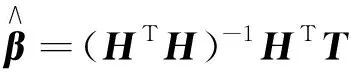
(6)

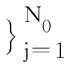
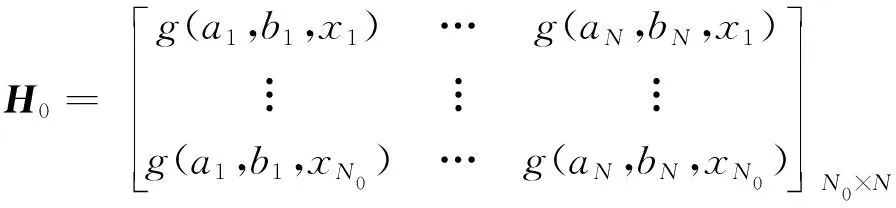
(7)

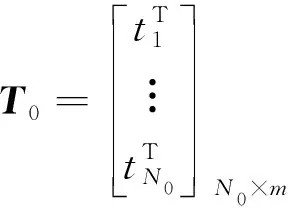
(8)

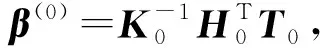
(9)

所以

其中

(11)

由此可知:

(12)

由此可以得到递推公式

(13)

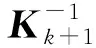
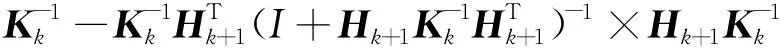
(14)

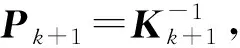
(15)

由上面的推导可知,OS-ELM在建立软测量模型时，输入的数据数量可以变化，在随着工况不断变化的同时，新的输入数据也会及时修正模型，并且在舍弃了旧的输入数据的情况下，提高了运行速度，软测量模型的准确性和可靠性得到显著提高[13]。

2 ADHDP原理

设刮膜蒸发过程的离散时间非线性动态系统

x(k+1)=f[x(k),u(k),k]

k=0,1,…

(16)

式中:x∈Rn——系统的状态向量；

x∈Rm——控制动作；

f——系统函数。

系统性能指标函数为：

(17)

式中:U——效用函数；

γ——折扣因子，0<γ≤1；

J——依赖于初始时间k和初始状态x(k)的性能指标函数。

ADHDP的目标是选出最优的控制序列u(i),i=k,k+1,…，使得式(17)定义的函数最小化。

ADHDP控制器结构包含3个典型网络。模型网络(Model Network)用来估计下一时刻的系统状态；评价网络(Critic Network)用来近似最优性能指标函数；执行网络(Action Network)为状态变量到控制变量之间的映射[14]。ADHDP学习控制器结构如图2所示。

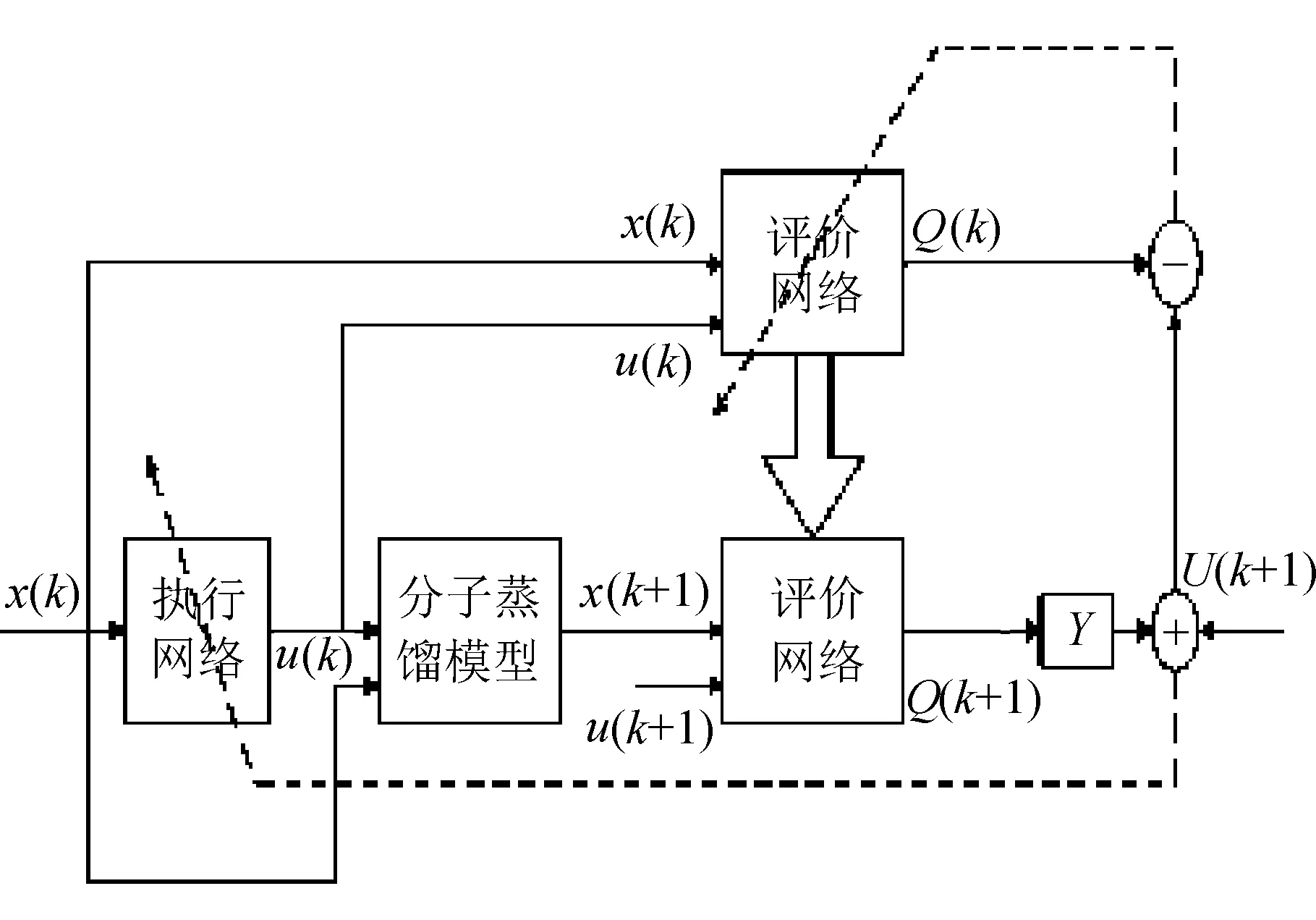
图2 ADHDP学习控制器结构

图2中Q函数是对性能指标函数的预估,可以写成如下表达式

Q(x(k))=U(x(k),u(x(k)))+Q(x(k+1))

(18)

式中：u(x(k))——反馈控制变量;

Q(x(k)),Q(x(k+1))——性能指标函数,评价网络的输出。

如果评价网络的权值设为Wc,可以令式的右式为：

D(x(k),Wc)=U(x(k),u(x(k)))+Q(x(k+1),Wc)

(19)

同时，式(19)的左式可以写为Q(x(k),Wc),因此可以通过调节评价神经网络权值最小化均方误差函数

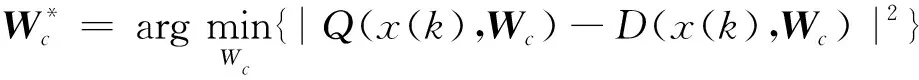
(20)

获得最优性能指标函数根据最优性原理，最优控制应满足一阶微分必要条件，所以有

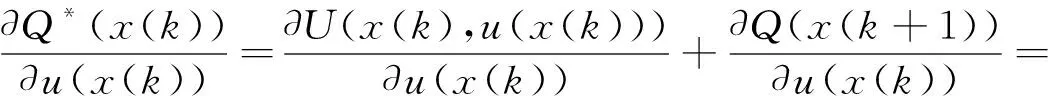
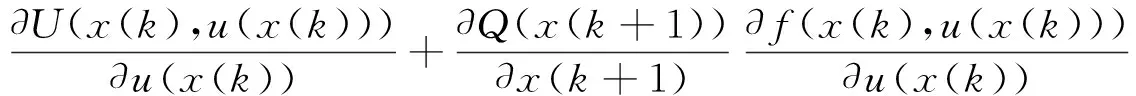
(21)

因此得到最优控制

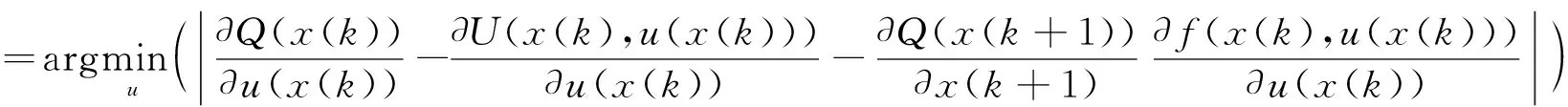
(22)

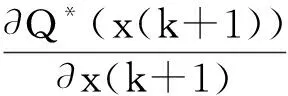
3 ADHDP训练评价网络和执行网络

ADHDP控制器包含由BP神经网络实现的执行网络和评价网络，以及刮膜蒸发过程的OS-ELM软测量模型。执行网络和评价网络的隐藏层采用双极性sigmoidal函数，输出层采用线性函数purelin，推导评价网络和执行网络的具体实现方法。

3.1 评价网络

评价网络输出为性能指标函数Q(k)，应满足式(18)，其训练最小化误差为：

(23)

ec(k)=Q(k)-U(k+1)-Q(k+1)

(24)

为了获得较快的收敛速度，将效用函数U(k)定义为二次型形式，定义如下:

U(k)=x(k)Ax(k)T+u(k)Bu(k)T

(25)

式中：A、B——分别为2维与4维的单位矩阵。

权值更新过程推导如下：

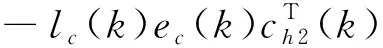
(26)

Wc2(k+1)=Wc2(k)+ΔWc2(k)

(27)

式中：lc——评价网络的学习率；

ch2(k)——隐含层的输出值。

(28)

式中：C(k)——评价网路的输入矩阵；

ch1(k)——隐含层的输入值。

Wc1(k+1)=Wc1(k)+ΔWc1(k)

(29)

3.2 执行网络

执行网络用于计算控制量，以使Q(k)最小为目标。

Ea(k)=Q(k)=γQ(k+1)+U(k+1)

(30)

权值更新过程推导如下：

⋮

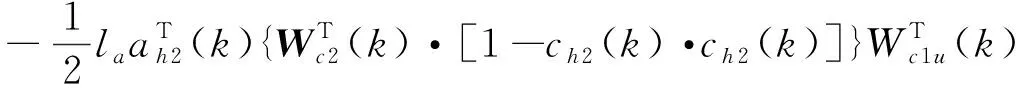
(31)

式中，Wa为执行网络权值，Wc1u=Wc1(1:m,:)，即Wc1的前m行，这里m=4，即与控制量对应的部分权值，la为执行网络的学习率。

Wa2(k+1)=Wa2(k)+ΔWa2(k)

(32)

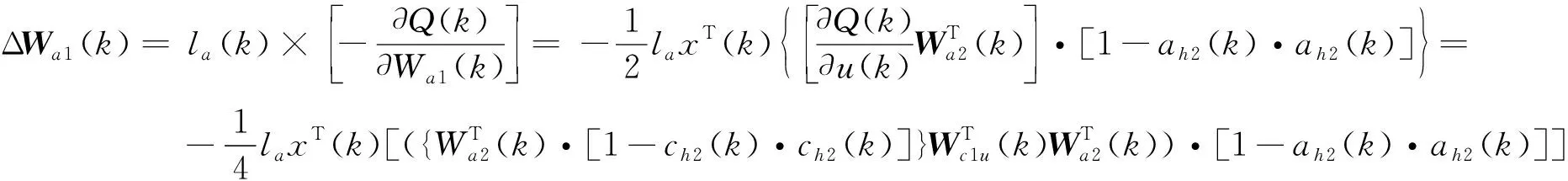
(33)

Wa1(k+1)=Wa1(k)+ΔWa1(k)

(34)

综上，ADHDP控制器的实现步骤如图3所示。

4 仿真实验

文中训练OS-ELM软测量模型的数据来源于刮膜式分子蒸馏装置针对东北地道药材五味子分离提纯过程的数据。刮膜式三级分子蒸馏装置由前级脱气、分子蒸馏1和分子蒸馏2三大部分组成，控制和监控各级工艺参数分别由PID仪表和计算机实现，第一、第二两级用于除去五味子原料油中水分和杂质且相关工艺参数固定，采集第三级的控制量、状态量的离线和在线数据。

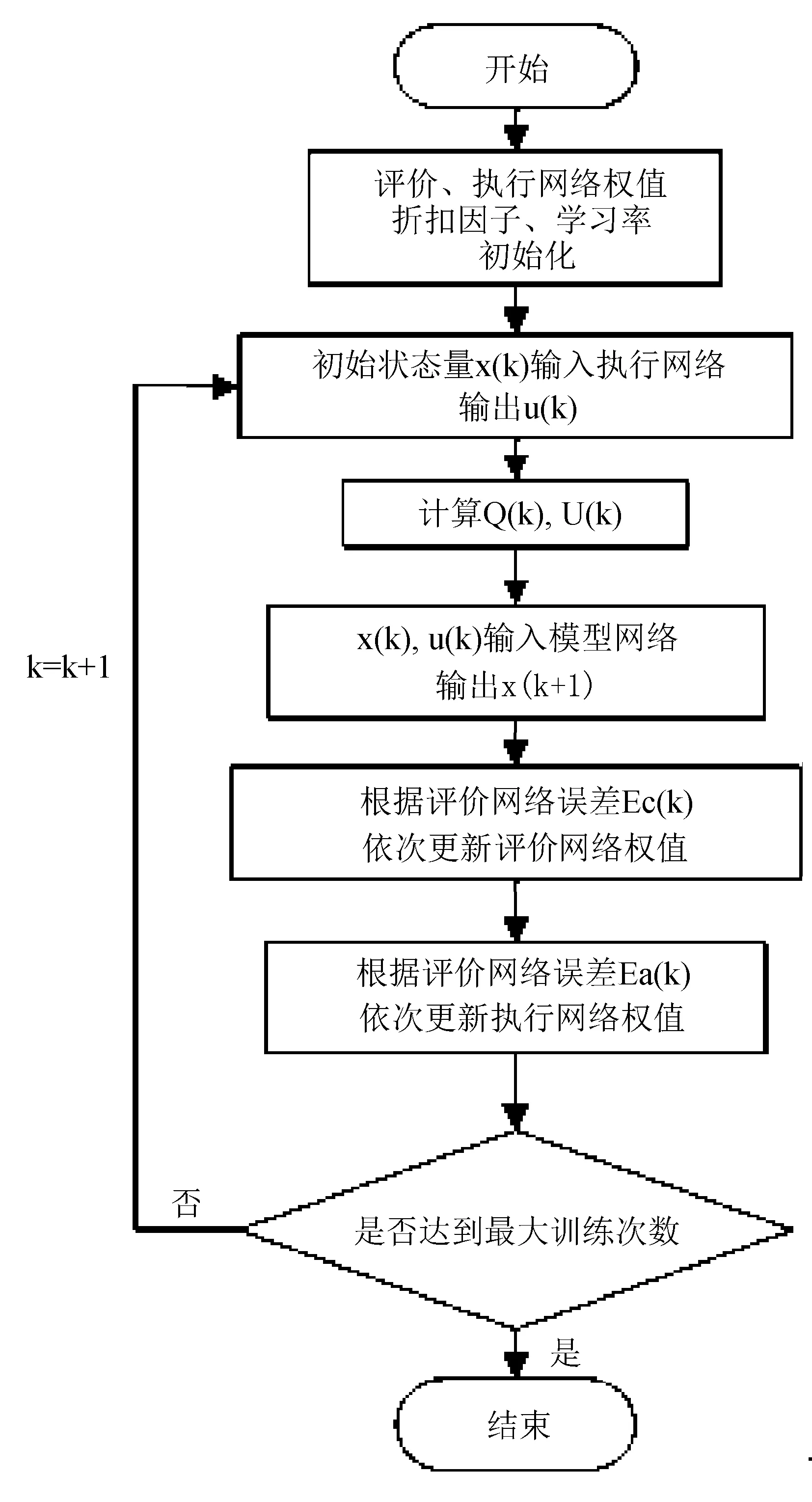
图3 ADHDP训练流程图

选择系统压力、温度、进料流量和刮膜电机转速作为控制变量，纯度作为状态变量，设定网络输入为6，输出为2，选取600组作为训练数据，150组数据用来进行预测，OS-ELM网络与BP网络的仿真结果对比如图4所示。

.

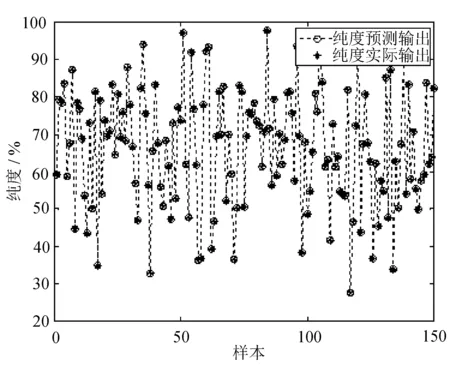
(a) OS-ELM纯度预测

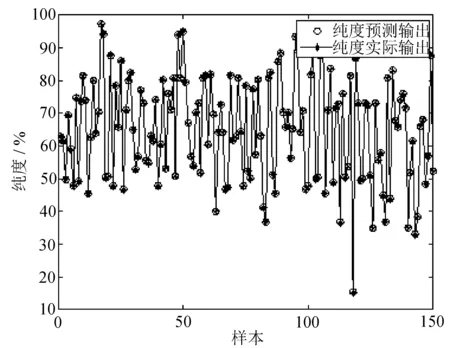
(b) BP纯度预测

具体性能参数对比见表1。

表1 OS-ELM与BP模型网络性能对比

从表1可以看出，OS-ELM软测量模型的误差和训练时间都远远小于BP软测量模型，并且随着数据的更新持续地对模型进行修正，证明了OS-ELM模型的优越性。

参数设置会在一定程度上影响算法的收敛速度。经过实验选取BP-ADHDP与OSELM-ADHDP的评价网络和执行网络的结构均为6-14-2和2-5-4，学习率为0.1，折扣因子为0.5，迭代步数为50，在刮膜蒸发过程中对系统压力、温度、进料流量、刮膜电机转速和纯度参数的寻优结果对比分别如图5～图9所示。

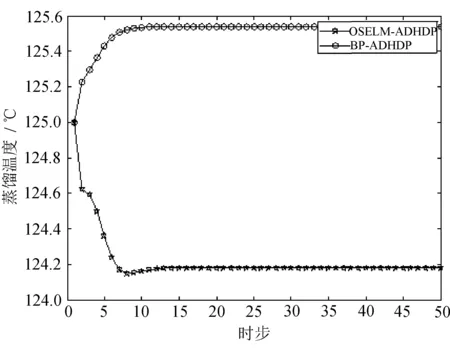
图5 控制量温度变化曲线图

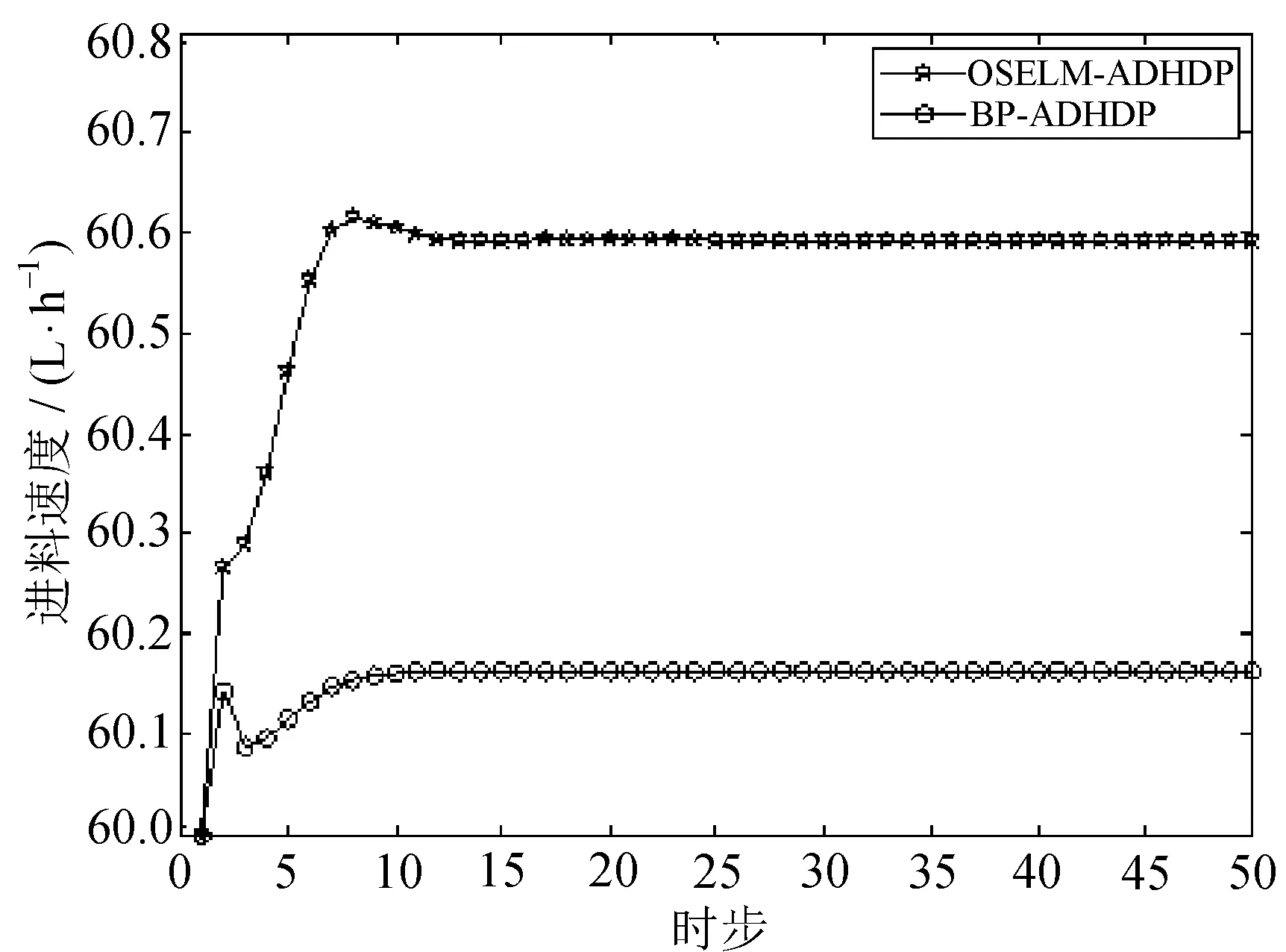
图6 控制量进料速度变化曲线图

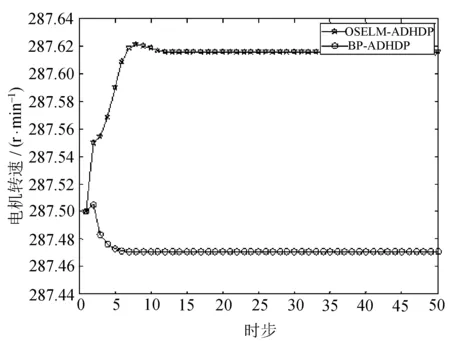
图7 控制量刮膜电机转速变化曲线

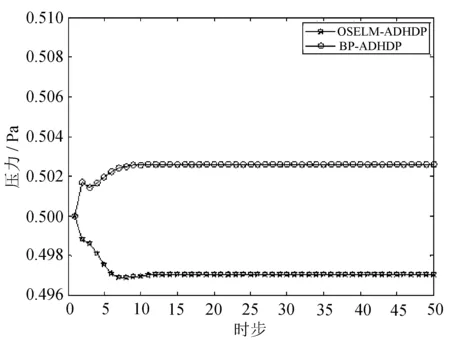
图8 控制量压力变化曲线图

由仿真结果可以看出,BP-ADHDP与OSELM-ADHDP大约都在13时步左右趋于稳定，但是,OSELM-ADHDP最优状态量纯度为95.58%，要远大于BP-ADHDP的89.93%，优化的状态量纯度得到了显著提高，并且OSELM-ADHDP模型网络更加准确可靠，能够实现更好的控制优化效果。

BP-ADHDP与OSELM-ADHDP最优控制量与状态量对比见表2。

5 结 语

分子蒸馏系统本身的多参数、强耦合、非线性决定其难以获得精确数学模型，在刮膜蒸发过程中的重要参数只能依赖于人工经验，以致难以实现稳定有效的控制，采用基于数据驱动的OS-ELM软测量模型，可以根据实际工况对模型进行调整，运用ADHDP对刮膜蒸发过程进行优化控制，仿真结果表明，系统训练时间短、超调量小，能够快速达到稳定状态，对提高刮膜蒸发过程的稳定性和高效性具有一定的指导意义。

表2 BP-ADHDP与OSELM-ADHDP最优控制量与状态量对比

参考文献：

[1] 连锦花,孙果宋,雷福厚.分子蒸馏技术及其应用[J].化工技术与开发,2010,39(7):32-38.

[2] 曹鹏飞,罗雄麟.化工过程软测量建模方法研究进展[J].化工学报,2013,64(3):788-800.

[3] Cvengroš J, Badin V, Pollák S. Residence time distribution in a wiped liquid film [J]. Chemical Engineering Journal and the Biochemistry Engineering Journal,1995(5):259-263.

[4] Cvengro J, Pollá K, Micov M. Film wiping in the molecular evaporator [J]. Chemical Engineering Journal,2001(1/2/3):9-14.

[5] Mckenna Timothy F. Design model of a wiped film evaporator applications to the devolatilisation of polymer melts [J]. Chemical Engineering Science,1995(3):453-467.

[6] Rong H J， Huang G B， Sundararajan N． Online sequential fuzzy extreme learning machine for function approximation and classification problems [J]. IEEE Transactions on Systems Man and Cybernetics Part B，2009，39(4)：1067-1072.

[7] Liang N Y, Huang G B, Paramasivan S, et al． A fast and accurate online sequential learning algorithm for feedforward netwroks[J]. IEEE Transactionson Neural Networks,2006,17(6)：1411-1423.

[8] 徐畅,许松林.刮膜式分子蒸馏停留时间分布的CFD模拟研究[J].安徽师范大学学报,2013,36(2):141-145.

[9] 王燕飞.刮膜式分子蒸馏过程流体流动的模拟与验证[D].天津：天津大学，2007.

[10] 王玲.刮膜式分子蒸馏器液膜停留时间分布及传热研究[D].天津：天津大学,2012.

[11] 李慧,王珂鑫.刮膜式分子蒸馏传质模型及其仿真[J].化工学报,2015，66(3):1026-1034.

[12] 李慧,李秀歌,王佳增.负压低温蒸馏装置的温度控制[J].长春工业大学学报：自然科学版,2014,35(5):516-523.

[13] 杨易旻.基于极限学习的系统辨识方法及应用研究[D].长沙：湖南大学,2013.

[14] 林小峰，宋绍剑，宋春宁.基于自适应动态规划的智能优化控制[M].北京：科学出版社,2013.

[15] 罗艳红.基于神经网络的非线性系统自适应优化控制研究[D].沈阳：东北大学,2008.