基于Monte-Carlo法的圆锥形黑体腔有效发射率的研究
沈久利, 邢婷婷, 吴 飞(燕山大学 电气工程学院, 河北 秦皇岛 066004)
1 引 言
研究黑体腔结构形状对其有效发射率的影响是目前相关专业研究的重要方向[1~6],有效发射率的计算方法有多次反射法、积分方程法、有限元分析法及Monte-Carlo法等。1989年,谢植研究了黑体腔的多次反射理论和积分方程理论,并证明了这两种理论在腔体壁面为漫发射体时和漫反射体时结论的一致性[7]。2012年,蔡璐璐根据黑体辐射换热理论,建立黑体腔传感器积分发射率和表面发射率的数学模型,并以圆柱形黑体腔传感器为研究对象对黑体腔积分发射率的影响进行了研究[8,9]。2013年,徐赛峰用Monte-Carlo法对开口式高温黑体空腔的结构进行了研究[10]。2015年,吴飞等人利用积分方程理论和有限元热分析法建立了圆筒形黑体腔的结构模型,分析了结构参数的改变对黑体腔性能的影响[11,12]。2017年,邢婷婷等人又建立了基于Monte-Carlo的圆柱体黑体腔模型,与有限元热分析的圆柱形黑体腔模型进行了对比分析[13]。
本文在分析了圆柱形黑体腔模型的基础上,应用Monte-Carlo法对圆锥型黑体空腔有效发射率进行分析,并与有限元分析法所得结果进行对比,讨论了腔体几何参数、材料发射率、接收器到腔口距离等因素对空腔有效发射率的影响。
2 圆锥形黑体腔传感器模型
圆锥形黑体空腔结构模型如图1所示。图中:R为黑体腔半径;L为腔体长度;R0为开孔半径;θ为圆锥角;R1为探测器半径;H为探测器距离腔口距离。腔体有效发射率是指圆形探测器共轴放置在距离腔口H处时测量到的空腔发射率。
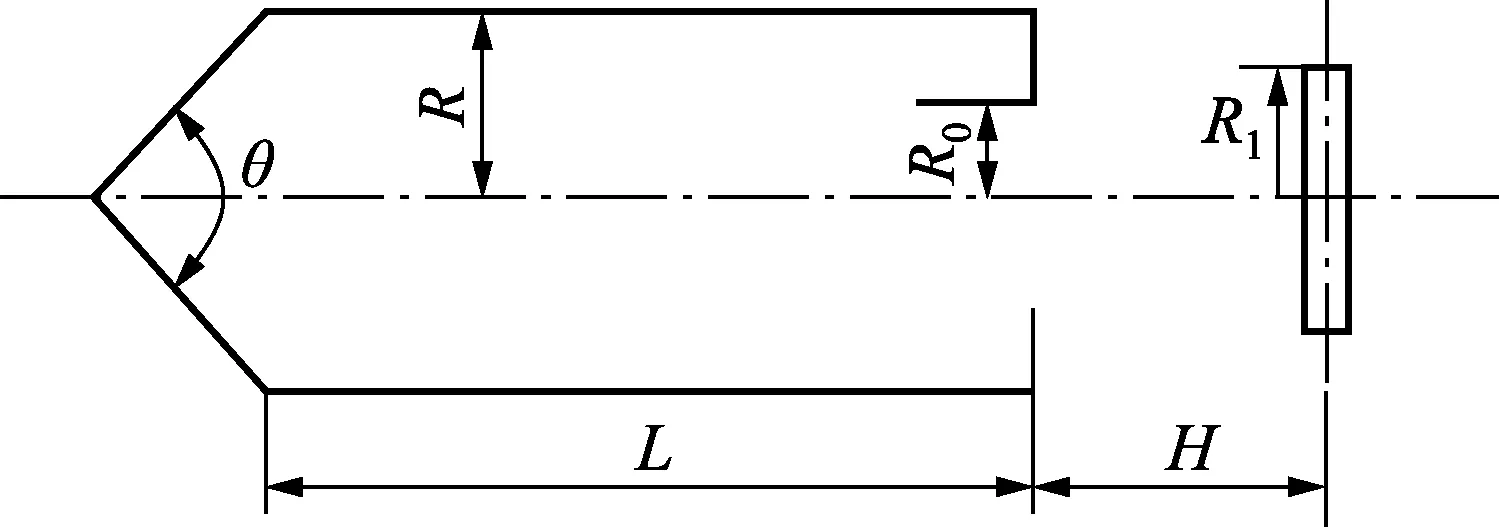
图1 圆锥形黑体空腔结构模型
3 Monte-Carlo法对黑体腔有效发射率的计算
基于Monte-Carlo方法计算黑体腔有效发射率采用逆向光线追迹算法。首先建立等温不透明的圆锥形黑体空腔,设定模拟光源发出的光线从腔外按一定方向入射至腔体内部,光束与腔壁产生反射,反射光能量衰减并继续反射,多次反射后直至光束射出腔口。通过计算反射出腔口光束的总能量与入射光束的总能量之比,即可确定空腔的有效反射率。
由基尔霍夫定律可知,当黑体腔处于热辐射平衡时,腔体的发射率在数值上等于吸收率,且有吸收率与反射率之和为1,如式(1)所示。
εe(λ,T)=∂e(λ,T)=1-ρe(λ,T)
(1)
式中:εe(λ,T)为等温空腔的有效发射率;∂e(λ,T)为有效吸收率;ρe(λ,T)为有效反射率;λ为波长;T为腔体温度。根据Monte-Carlo方法可得到:
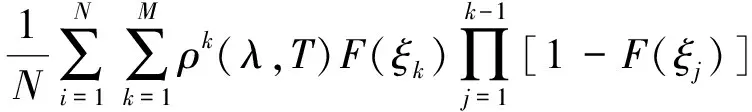
(2)
式中:N为光线总数目;M为反射总次数;ξ为反射点的位置;Wi为第i束光线的光束能量;ρk(λ,T)为光线第k次反射的反射系数;F(ξ)为反射点ξ对空腔口的角系数。由式(1)、(2)计算出黑体腔有效发射率。
假设圆锥形黑体腔半径R=1为单位长度,定义腔体长度和半径比为L/R(简称为长径比),开孔半径和半径比为R0/R(简称为孔径比)。当L/R=6,R0/R=0.5,圆锥角θ=90°,材料发射率为0.1时,光束经过黑体空腔出射后,辐射在探测器接收面上的辐照度分布情况如图2。出射光束的能量分布类似高斯曲线,接收面中心部分能量最高,由中心向四周衰减。通过改变空腔几何结构参数,可得不同的辐照度分析图,经计算得到腔体有效发射率。

图2 探测器接收面辐照度分布注:最小值:4.296×10-16;最大值:2.487 7×10-4;均值:2.161 9×10-5; 总光通量:0.007 711 3 W;光通量/发射光通量:0.043 779; 13 190条光线
4 圆锥形黑体腔传感器参数对比分析
影响腔体有效发射率的主要因素有:腔体几何参数、材料发射率以及探测器到腔口的距离。下面采用Monte-Carlo法进行计算,并与有限元分析法所得的结果进行对比,说明腔体的最佳参数选择。
4.1 腔体L/R的影响
假设黑体腔半径R=1为单位长度,圆锥角θ=90°,腔体R0/R=0.5。分析不同材料发射率下,腔体L/R对空腔发射率的影响如图3所示。图3(a)和图3(b)分别表示材料发射率取0.1和0.5时,分别由Monte-Carlo法和有限元分析法得到的腔体L/R对空腔有效发射率的影响。
由图3可知,两种方法得到的结果基本相同,即:空腔的有效发射率与腔体的L/R正相关。L/R越大,则有效发射率越大,但是当L/R达到6时,有效发射率增加量减小,趋于平稳。考虑腔体的成本,一般可选择L/R为6。
4.2 腔体R0/R的影响
假设黑体腔半径R=1为单位长度,圆锥角θ=90°,腔体L/R=6。不同材料发射率下,腔体R0/R对空腔发射率的影响如图4所示。图4(a)和图4(b)分别表示材料发射率取0.1和0.5时,分别由Monte-Carlo法和有限元分析法得到的腔体R0/R对空腔有效发射率的影响。
由图4可知,随着腔体R0/R增加,空腔有效发射率减小,尤其是在材料发射率较小时,空腔有效发射率减小的趋势更为明显。而在材料发射率较大时,空腔的有效发射率减小不明显。所以,考虑到R0/R与探测器的视场关系,一般选择R0/R为0.5。

图3 不同发射率空腔L/R与腔体有效发射率的影响关系
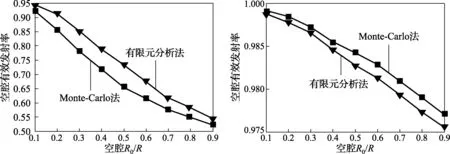
图4 不同发射率空腔R0/R与腔体有效发射率的影响关系
4.3 腔体圆锥角θ的影响
假设黑体腔半径R=1为单位长度,腔体L/R=6,腔体R0/R=0.5。分析不同材料发射率下,腔体圆锥角θ对空腔发射率的影响。如图5所示,图5(a)和图5(b)分别表示材料发射率取0.1和0.5时,由Monte-Carlo法和有限元分析法得到的腔体圆锥角θ对空腔有效发射率的影响。
由图5可知,随着θ的增加,空腔有效发射率增加,当θ=90°时,空腔有效发射率趋于平稳。而在材料发射率较大时,空腔的有效发射率增加不明显。所以,考虑到腔体的制作难度,一般选择θ=90°。
4.4 材料发射率的影响
假设黑体腔R=1为单位长度,θ=90°,腔体R0/R=0.5、L/R=6,分析不同材料发射率对空腔发射率的影响。图6为Monte-Carlo法和有限元分析法得到的材料发射率对空腔有效发射率的影响。
由图6可知,随着材料发射率的增加,空腔有效发射率也增加,当材料发射率达到0.5时,空腔有效发射率趋于平稳。所以,在选择材料时不必追求其本身具有过高的发射率,一般选择材料发射率为0.5~0.6。
4.5 探测器到腔口距离H的影响
假设黑体腔R=1 为单位长度,θ=90°,腔体R0/R=0.5,腔体L/R=6,材料发射率为0.1。

图5 不同发射率θ与腔体有效发射率的影响关系
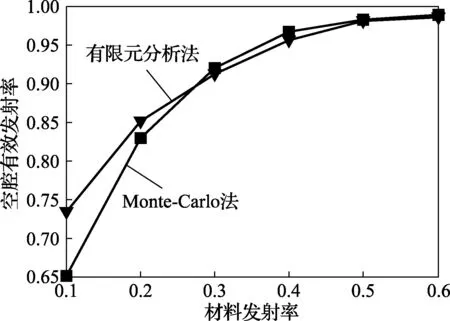
图6 材料发射率与腔体有效发射率的影响关系
分析探测器到腔口距离H对空腔有效发射率的影响。图7为Monte-Carlo法和有限元分析法得到的探测器到腔口距离H对空腔有效发射率的影响。由图7可知,随着H的增加,空腔有效发射率先快速增加,然后减小,趋于稳定。当H达到腔体半径15倍时,空腔有效发射率较大。所以,一般选择H为腔体半径的15倍。
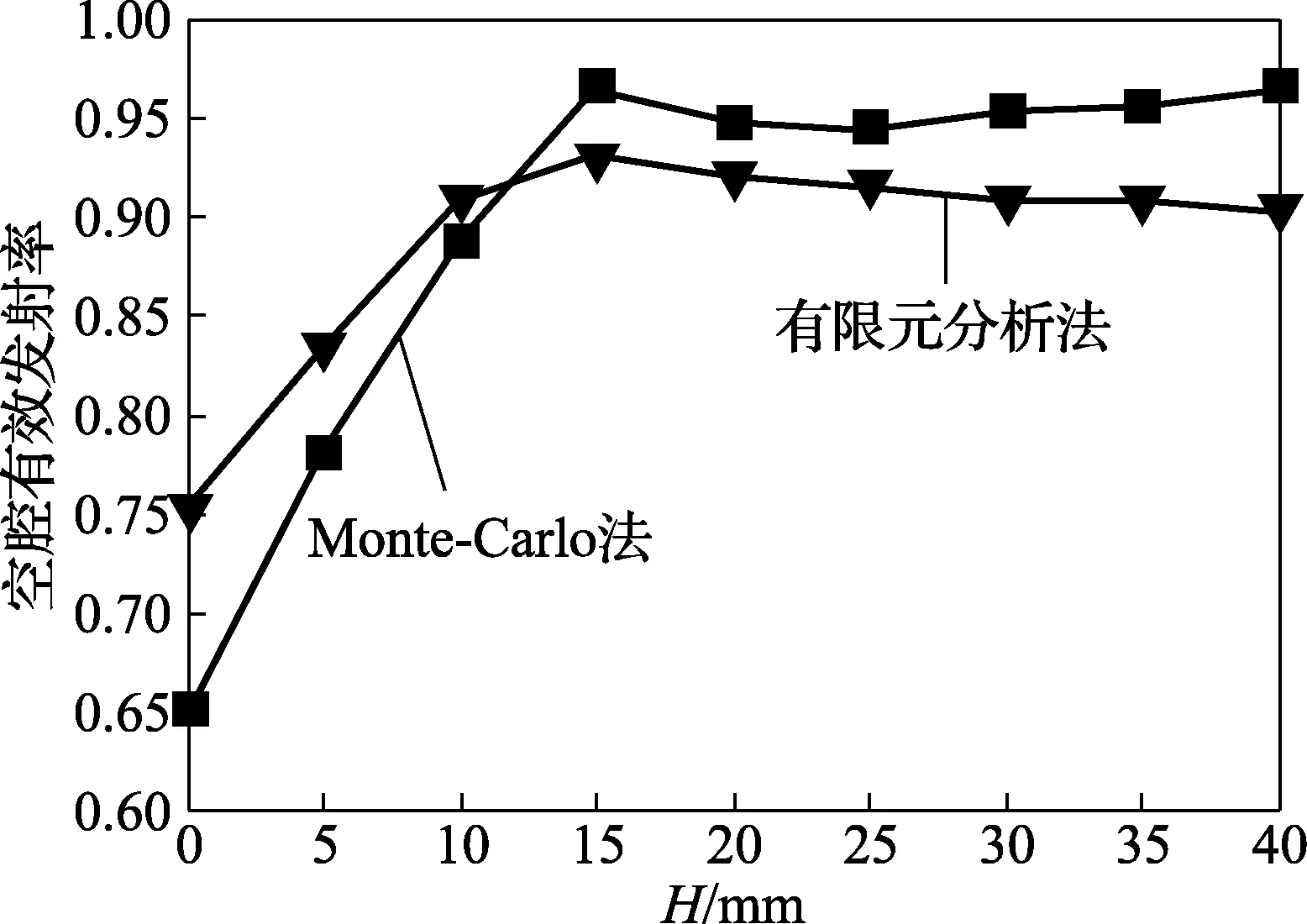
图7 探测器到腔口距离与腔体有效发射率的影响关系
5 结 论
通过对比Monte-Carlo法和有限元分析法得到的结果,圆锥形黑体腔有效发射率随腔体几何参数、材料发射率以及探测器到腔口的距离变化的趋势基本一致。在考虑实际应用的条件下,为了得到较高的圆锥形黑体腔有效发射率,应选择参数为:L/R=6,R0/R=0.5,θ=90°,材料发射率为0.5~0.6,H为腔体半径的15倍。
[参考文献]
[1] Fang Q Q, Fang W, Wang Y P,etal. New shape of blackbody cavity: conical generatrix with an inclined bottom[J].OpticalEngineering, 2012, 51(8):6401.
[2] 李文军,孙坚,邹超,等.黑体空腔辐射理论和设计[J].计量学报,2011,32(2):137-140.
[3] 郑龙江,常蕾,吴飞,等.高温黑体空腔发射率有限元分析[J].红外与激光工程,2011,40(9):1640-1645.
[4] 孙富韬.Monte-Carlo方法在黑体空腔有效发射率计算中的应用[J].宇航计测技术,2010,(2):26-29.
[5] 黄燊彦,郝小鹏,王景辉,等.铯、钠热管标准黑体辐射源研制及性能评价[J].计量学报,2014,35(2):120-124.
[6] 原遵东,郝小鹏,王景辉,等.黑体辐射源的多波长有效亮度温度校准和不同溯源方式特点分析[J]. 计量学报,2017,38(2):135-140.
[7] 谢植,高魁明.论黑体空腔多次反射理论和积分方程理论的统一性[J].计量学报,1989,10(2):101-104.
[8] 蔡璐璐.基于黑体腔特性的光纤高温测试技术及系统的研究[D].秦皇岛:燕山大学,2012.
[9] 蔡璐璐,田海霞,吴飞,等.高温黑体腔有效发射率的计算[J].计量学报,2016,37(6):602-605.
[10] 徐赛锋.高温黑体辐射源研究与设计[D].南京:南京理工大学,2013.
[11] 吴飞,董杰,田海霞,等.黑体腔高温传感器结构设计[J].红外与激光工程,2015.44(9):2609-2614.
[12] 吴飞,董杰,田海霞,等.基于有限元的黑体腔高温传感器动态特性分析[J].传感器与微系统,2015,34(8):35-38.
[13] 邢婷婷,沈久利,蔡璐璐.Monte-Carlo法的黑体腔高温传感器有效发射率研究[J].传感器与微系统,2017,36(6):7-9.

