基于三维点云聚类的坡度估计方法

李海波， 曹云峰， 丁 萌， 庄丽葵(南京航空航天大学， 江苏 南京 210016)

1 引 言

为了对火星进行更全面的科学考察，通常需要探测器着陆到火星表面。探测器在着陆过程中，应避免着陆到坡度较大的斜坡上，以免造成侧滑或倾翻[1]。因此探测器在着陆阶段，需要对候选着陆区域的坡度进行估计。火星表面存在较大的岩石[2],岩石会使岩石区域的测量数据相对周围区域测量数据产生较大的突兀值，影响坡度估计。目前,对坡度的估计方法主要有基于机器视觉的方法与基于激光雷达(light detection and ranging，LIDAR)的方法。机器视觉在计量领域有多种应用[3～5]，其设备具有体积小、重量轻的优点，但获得的数据受光照变化影响大;激光雷达可以应用到不同测量目标上[6,7]，其测量数据不受光照影响，是一种理想的坡度估计信息源;文献[8]提出了一种利用激光雷达测量数据进行坡度估计的方法，该方法采用最小二乘法拟合平面，拟合平面的倾角即为该区域的坡度;文献[9]也提出了一种基于激光雷达测量的高程数据进行坡度估计的方法，该方法采用最小平方中位数法求取局部地形的法向量，法向量与天体重力方向的夹角即认为是局部地形的坡度，但该方法需要预先设定一些先验参数;文献[10]针对激光雷达测量的数据利用最小二乘法拟合一个平面，求取该平面的法向量，定义法向量与当地重力加速度方向之间所夹的锐角即为局部地形坡度，也就是拟合平面与基准面之间的夹角;此外其他相关文献中关于坡度估计的方法大都基于上述方法，如文献[11]等。但这些方法对坡度进行估计均存在估计误差较大的问题，为此，本文研究了一种基于三维点云数据聚类与随机搜索最优拟合平面的坡度估计方法，可以显著降低估计误差，提高坡度估计精度。

2 坡度估计原理

2.1 测量数据点的稀疏表示

首先定义测量区域空间坐标系，其定义及数据点三维表示如图1所示。空间直角坐标系在三维激光扫描测量中起着关键作用[12]，以测量区域的左下角为原点，x轴与水平边重合指向正东；y轴与x轴垂直，指向正北；z轴与x轴和y轴垂直并按右手定则确定，见图1(a)。通过空间坐标系，激光雷达的测量数据可用三维坐标表示，即Di=[xi,yi,zi]，其中，D表示数据点；i为测量点数据序号;x、y、z分别表示测量点数据在三轴上的坐标，见图1(b)，图中模拟的数据点可用三维坐标表示。

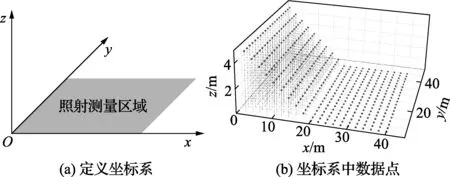
图1 坐标系定义及数据点三维表示

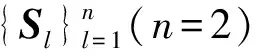
X[x1…xN]=[X1…Xn]Γ

(1)

式中：Xl∈R3×Nl；Γ∈RN×N，是未知的置换矩阵。由于子空间的基是未知的，无法确定测量数据点属于哪个子空间。为解决这一问题，首先将数据点进行稀疏化表示，使每一个数据点可以用空间中少数其他数据点进行表示，即

xi=Xci,cii=0

(2)

式中：ci[ci1ci2…ciN]T；cii=0为限制条件，防止得到平凡解。由于在子空间中数据点的数量大于数据点的维数，解的形式不唯一，即每个数据点由其他数据点表示的方式不唯一，具有多种方式。在这些解中，存在一种稀疏解ci，其解的非零部分与来自同一子空间的数据点xi相对应[13]， 即对于子空间Sl中的任一数据点xi，可以用来自同一子空间中的其他数据点组合表示。因此，离散数据点的稀疏表示能够发现属于同一子空间的数据点。由于式(2)中存在多个解，故采用最小化解的1范数方式获得稀疏解，即

(3)

式(3)的解可通过凸规划工具求得[14～16]。通过式(3)，将所有数据点的稀疏优化写成矩阵形式：

(4)

式中:C[c1c2…cN]∈RN×N，其列向量对应数据点的稀疏表示。式(4)的解即为所有数据点的稀疏表示，解中非零元素与空间中数据点相对应。

2.2 测量数据点分割

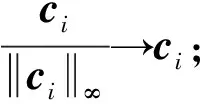
通过构造好的非负对称相似度矩阵W构造对角矩阵A，形式如下：

(5)

式中对角元素aii(i=1,…,N)为相似度矩阵W中列向量ci所有元素之和。利用对角矩阵A构建Laplacian矩阵，即L=I-A-1/2WA-1/2，I为单位矩阵。对构建的Laplacian矩阵L进行SVD(singular value decomposition)分解，对分解后得到的右正交矩阵V应用K-means算法进行聚类，从而完成对数据点的分割。

2.3 子空间测量点平面拟合

对分割后的子空间测量点单独进行平面拟合，设某一子空间测量数据点预确定的平面的方程为：

ax+by+cz=d

(6)

式中：a、b、c为所设定平面单位法向量中的元素值，即单位法向量为(a,b,c)，则有a2+b2+c2=1；d表示原点到所设定平面的距离，d≥0。

在子空间中随机选取一个数据点，计算与其欧式距离最近的4点，设这5点为{(xi,yi,zi),i=1,…,5}，由式(6)可知每个点到平面的距离为

hi=|axi+byi+czi-d|

(7)

式中h表示点到平面的距离。

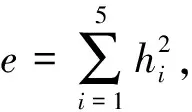
(8)

当e的值最小时，平面拟合最好。为求取e的最小值，根据约束条件：a2+b2+c2=1，利用拉格朗日乘子法构造函数如下：

λ(a2+b2+c2-1)

(9)

式中λ为拉格朗日乘子。

将式(9)对d求偏导,并令其为0，即

(10)

整理得

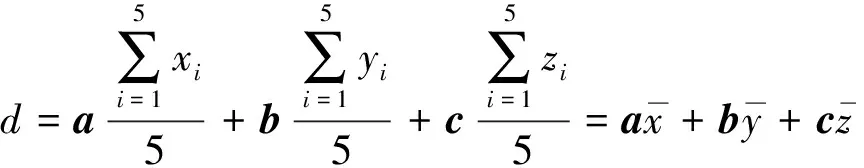
(11)

将式(11)代入式(7)得

(12)

将式(11)代入式(9)得

(13)

将式(13)分别对a、b、c求偏导,并令其为0，

(14)

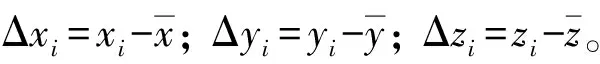
将式(14)进一步整理转换得：

(15)

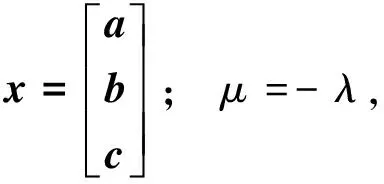
Bx=μx

(16)

B为3×3实对称矩阵，由矩阵理论可知：

(17)

式中(，)表示两个向量做点积运算。由于a2+b2+c2=1，所以(x,x)=1，则

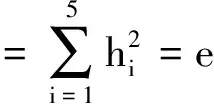
(18)

当e取最小值时拟合的平面最好，所以μ应取最小值，其对应的特征向量为a、b、c的值。

利用正交三角分解可求出矩阵B的所有特征值，设最小特征值为μmin，I为单位矩阵。求其对应的特征向量，令

(B-μminI)x=0

(19)

通过式(19)求得的非零解即为对应的特征向量，从而获得参数a、b、c的值，即平面的法向量元素值。将所求的a、b、c值代入式(11)中，可求出d的值。

设子空间中另一数据点为Dj={(xj,yj,zj),j=1,…,n,j≠i}，由式(7)可知，其与平面的距离为hj。当hj的值小于设定阈值时，则该点属于统计的点； 当hj的值大于或等于设定阈值时，该点不属于统计的点。

按此方法计算子空间中其余点与该平面的距离，统计与平面距离小于设定阈值的点，当统计的数目大于预先设定值时，便认为该平面为最优拟合平面，其法向量为(a,b,c)；若统计的数目小于或等于预先设定值，便认为该点不是最优拟合平面，需重新随机选取一点，重复上述步骤，直至统计的数目大于预先设置值为止。同理，用该方法可以求得另一子空间数据点的最优拟合平面及法向量。

2.4 坡度角估计

在获得两个最优拟合平面后，可以通过其法向量夹角求得两个平面的夹角，设两平面的法向量分别为n1、n2，则其夹角可通过下式计算。

(20)

式中θ为两法向量之间夹角。根据几何关系，θ在数值上等于两平面夹角，即坡度角。

3 仿真实验及分析

随机选取两个斜坡角度进行算法测量实验，模拟生成的待测量斜坡角度如图2所示。

如图2所示两种斜坡角度对应的模拟激光雷达测量数据点如图3所示。

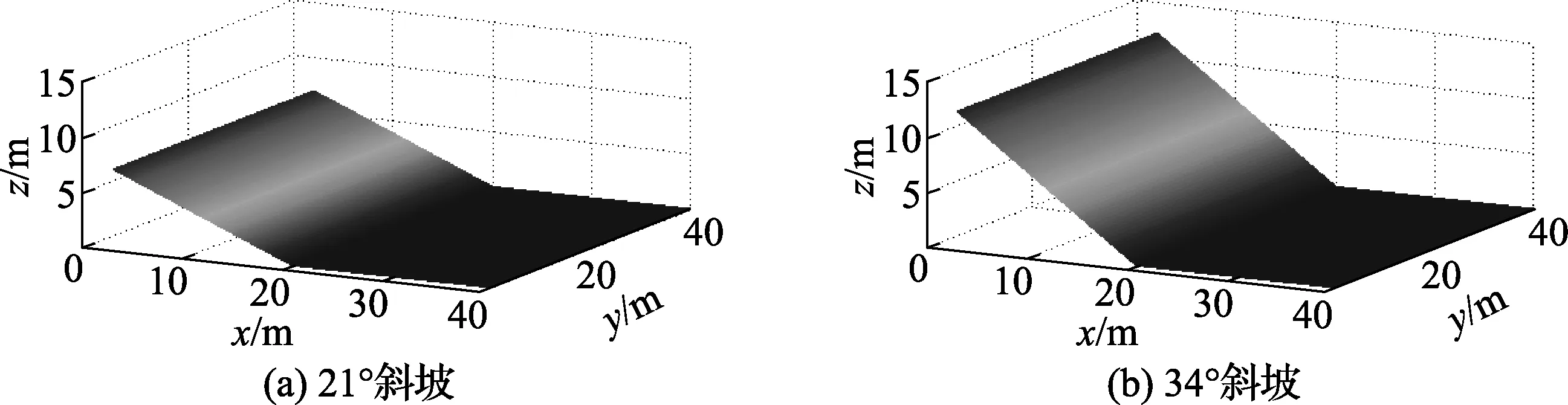
图2 模拟生成的待测量斜坡角度

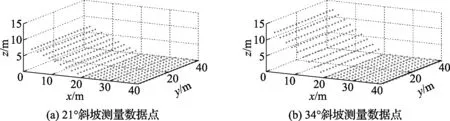
图3 斜坡角度测量数据点

对于图3的测量数据点，首先利用2.1节所述方法进行稀疏表示；在此基础上，利用2.2节所述方法进行数据分割，划分子空间数据点；对子空间数据点使用2.3节所述方法进行平面拟合，求出平面法向量；根据所求法向量，利用公式(20)计算两平面夹角，即坡度角，平面拟合及计算结果如图4所示。

对斜坡角度测量结果进行统计分析见表1。

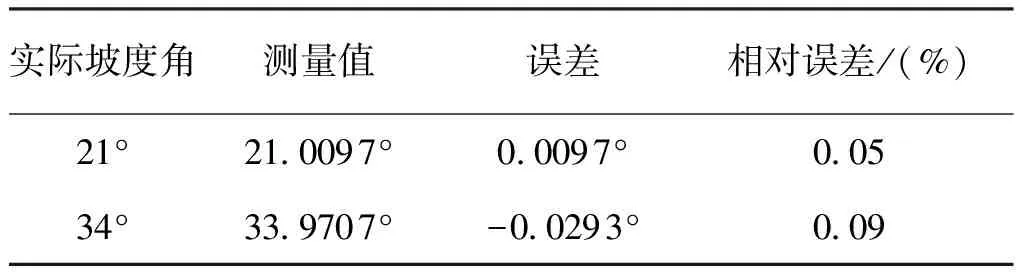
表1 测量结果分析

由表1可以看出，本文所述方法测量误差极小，测量相对误差较小。

考虑到在实际工作中坡度可能很不规则及火星地表存在较大岩石等情况，在34°斜坡上模拟添加存在上述情况产生的突出测量值，如图5(a)中椭圆内的测量值。利用2.2、2.3节所述方法对数据点进行分割与寻找最优平面拟合数据点，数据点寻找结果如图5(b)所示，可以看出突出测量值数据点没有被统计到拟合数据点范围内，利用图5(b)所示的数据点进行平面拟合，结果如图5(c)所示。

从图5(c)可以看出，坡度测量结果为33.970 7°，与图4(b)的测量结果相同，这表明本方法对突出的测量值具有一定的鲁棒性。

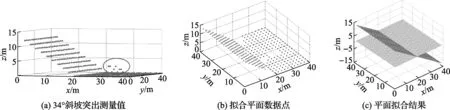
图5 存在突出测量值的坡度估计

4 与常用方法比较

利用激光雷达测量数据进行坡度估计的常用方法是最小二乘法(least square method,LSM)，将文中提出的方法与最小二乘法进行比较。随机选取一个坡度，模拟生成的斜坡角度及测量数据点如图6所示。分别用最小二乘法和本方法对测量数据进行处理，计算结果如图7所示。对测量结果进行比较分析，结果如表2所示。从表2可以看出，本文提出的方法测量相对误差较小；与LSM方法比较，测量误差得到了显著降低。

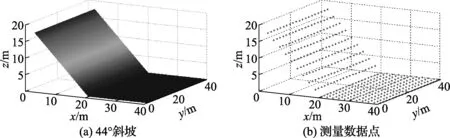
图6 44°斜坡及测量数据点

图7 测量结果比较

表2 不同方法测量结果比较分析

5 结 论

为降低火星探测器着陆时对坡度估计的误差，研究了一种基于三维点云数据聚类与随机搜索最优拟合平面的坡度估计方法。对于三维点云测量数据，首先进行数据点的稀疏表示；然后根据稀疏表示系数对数据点进行聚类与分割，划分子空间；对子空间中的数据点进行平面拟合，随机搜索最优拟合平面；根据最优拟合平面计算其法向量及向量间夹角，完成坡度估计。实验表明：本文方法可以对坡度进行较为准确的估计,与常用的坡度估计方法相比较，可以显著降低估计误差，提高坡度估计精度，为探测器着陆时决策是否需要规避机动提供更加准确的信息。

[参考文献]

[1] Lunghi P, Ciarambino M, Lavagna M. A multilayer perceptron hazard detector for vision-based autonomous planetary landing[J].AdvancesinSpaceResearch,2016,58(1):131-144.

[2] Craddock R A, Golombek M P. Characteristics of terrestrial basaltic rock populations:Implications for Mars lander and rover science and safety[J].Icarus,2016,274:50-72.

[3] 刘庆民,张蕾,吴立群,等.基于机器视觉的非均匀分布点圆度误差评定[J].计量学报,2016,37(6):567-570.

[4] 刘源泂,孔建益,徐福军,等.基于图像金字塔的钢板表面深度信息提取方法[J].计量学报,2015,36(4):356-359.

[5] 朱奇光,张兴家,陈卫东,等.基于颜色矩的改进尺度不变特征变换的移动机器人定位算法[J].计量学报,2016,37(2):118-122.

[6] 王涛,仲思东.弹丸三维轮廓激光扫描测量方法[J].计量技术,2015,(2):14-18.

[7] 魏凯,宋述古,刘子勇.基于三维激光扫描原理的球形罐容量计量方法研究[J].计量学报,2015,36(6):607-609.

[8] 梁栋,王鹏基,刘良栋.一种基于LIDAR的精确月球软着陆目标点选定方法[J].空间控制技术与应用,2009,35(6):24-29.

[9] 姜肖楠,韩诚山,李祥之.多传感器月面障碍模糊识别方法[J].计算机仿真,2013,30(4):97-102.

[10] 张泽旭,王卫东,崔平远,等.一种行星软着陆地形风险评估方法[J].哈尔滨工业大学学报,2011,43(5):25-29.

[11] 于正湜,朱圣英,崔平远.基于LIDAR的月球着陆区评估与选择方法[C]// 中国宇航学会深空探测技术专业委员会第九届学术年会.杭州,2012.

[12] 李明慈,黄桂平,李冰,等.坐标转换在应用中的问题及解决方法[J].计量技术,2015,(8):25-28.

[13] Elhamifar E, Vidal R. Sparse subspace clustering:algorithm,theory,and applications[J].IEEETransactionsonPatternAnalysis&MachineIntelligence,2013,35(11):2765-2781.

[14] Boyd S, Vandenberghe L, Faybusovich L. Convex Optimization[J].IEEETransactionsonAutomaticControl,2006,51(11):1859-1859.

[15] Kim S J, Koh K, Lustig M,etal. An Interior-Point Method for Large-Scale l1-Regularized Least Squares[J].IEEEJournalofSelectedTopicsinSignalProcessing,2007,1(4):606-617.

[16] Boyd S, Parikh N, Chu E,etal. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers[J].FoundationsandTrendsinMachineLearning,2011,3(1):1-122.