汽车发动机进气歧管高精度亚像素边缘检测

徐 平, 薛凌云, 常英杰(杭州电子科技大学 生命信息与仪器工程学院, 浙江 杭州 310018)

1 引 言

汽车发动机进气歧管的尺寸检测是生产厂家评价产品质量的重要指标,现有的检测手段主要依赖人工接触式测量,效率低且可靠性不高,实际测量结果无法准确获取。采用机器视觉技术对零件的尺寸、形状等几何特征进行检测已成为现代制造业中改进和控制产品质量的重要手段,其中,零件图像的边缘检测是该技术的关键和核心步骤。图像边缘检测的精确度直接影响着最后测量结果的精确度[1]。亚像素边缘检测相对于传统的Canny,Sobel等像素级的边缘检测具有更高的精度,目前,常用的亚像素边缘检测方法主要可分为3种类型:拟合法、插值法和矩方法[2,3]。文献[4,5]提出了将边缘梯度拟合为二次多项式曲面来进行亚像素边缘检测的方法,这些方法具有较好的抗噪能力,但存在计算复杂度高的不足;文献[6]提出了一种非线性四阶ENO (essentially non oscillatory)插值的方法,这类方法具有较好的计算效率但对于含噪图像的边缘检测效果不佳;文献[7]提出了一种基于正交Fourier-Mellin矩的方法(OFMM),矩方法对噪声比较敏感;文献[8]提出了一种新型的亚像素边缘检测方法,该方法利用边缘投影像素的矩形邻域内的灰度信息建立投影曲线方程得到高精度的亚像素边缘,但该方法直接将曲线的截距点作为边缘的亚像素位置,而没有考虑曲线的方向信息,在数学意义上,这不符合梯度的定义,同时,该方法在根据周围像素计算像素内的灰度值时采用的是各像素的均值,这并不符合成像时光斑能量分布的真实情况。

针对汽车进气歧管,本文在求得边缘投影曲线的基础上,提出将过原点且方向为梯度方向的直线与边缘曲线的交点作为高精度亚像素边缘点,并以此为长短轴尺寸测量的基础。同时,因为成像时光斑的能量分布为高斯分布[9],故本文在计算像素内的灰度值时,对其邻近灰度值进行了高斯加权处理,得到更高精度的汽车进气歧管长短轴检测结果。

2 算法实现

图1给出了算法实现的流程图。获取图像的像素级边缘是实现该方法的前提,本文通过以下步骤来获取图像的像素级边缘:首先,运用Sobel算子得到图像的梯度图;然后,对梯度图使用阈值分割得到高梯度值像素的集合;最后,对该集合进行骨架化处理得到单像素的边缘。

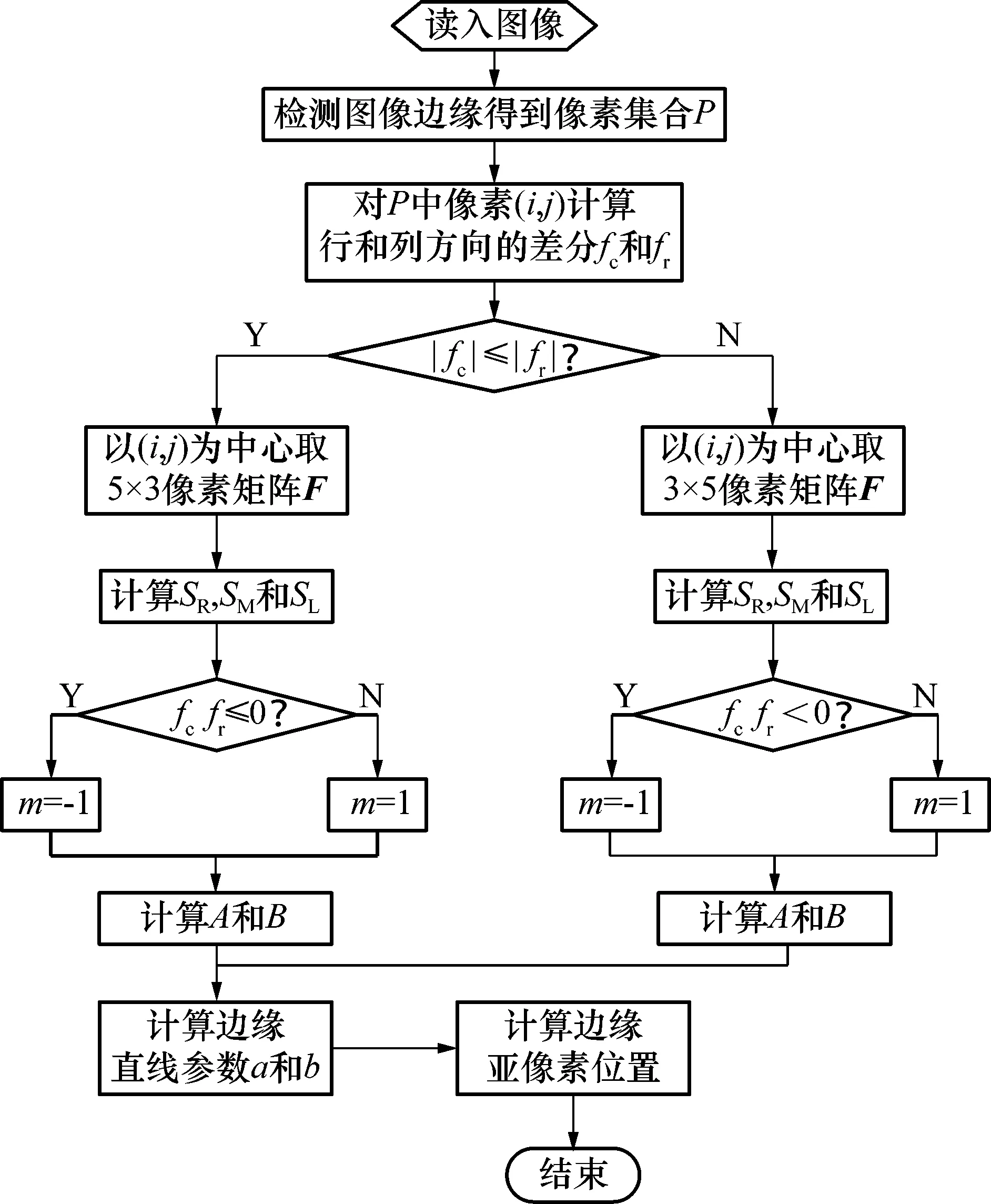
图1 算法流程图

获得图像的单像素边缘后,按照式(1)和式(2)计算每一个像素在行和列方向上的差分fc,fr:

(1)

(2)

2.1 |fc|≤|fr|的情况

单像素边缘中的每一个像素可认为是边缘投影所穿过的像素。对于任一像素(i,j),将穿过该像素的边缘投影近似成一段线段(线段方程设为y=a+bx,a为截距,b为斜率)。由于此时该像素的列差分fc和行差分fr满足|fc|≤|fr|,所以有b∈[-1,1]。在实际中待检测零件的边缘在一定范围内总是连续可导的,且像素单元的尺寸又很小,可近似认为所设直线也会穿越像素(i,j)所在列的邻近几列像素,因此把像素(i,j)所在的列以及与其邻近的左右两列像素作为研究对象。同时穿越3列像素(i,j)内部直线可能扫过的像素范围如图2所示。其中Y1为过极限位置1时的直线,Y2为过极限位置2时的直线,一共考虑5行像素。

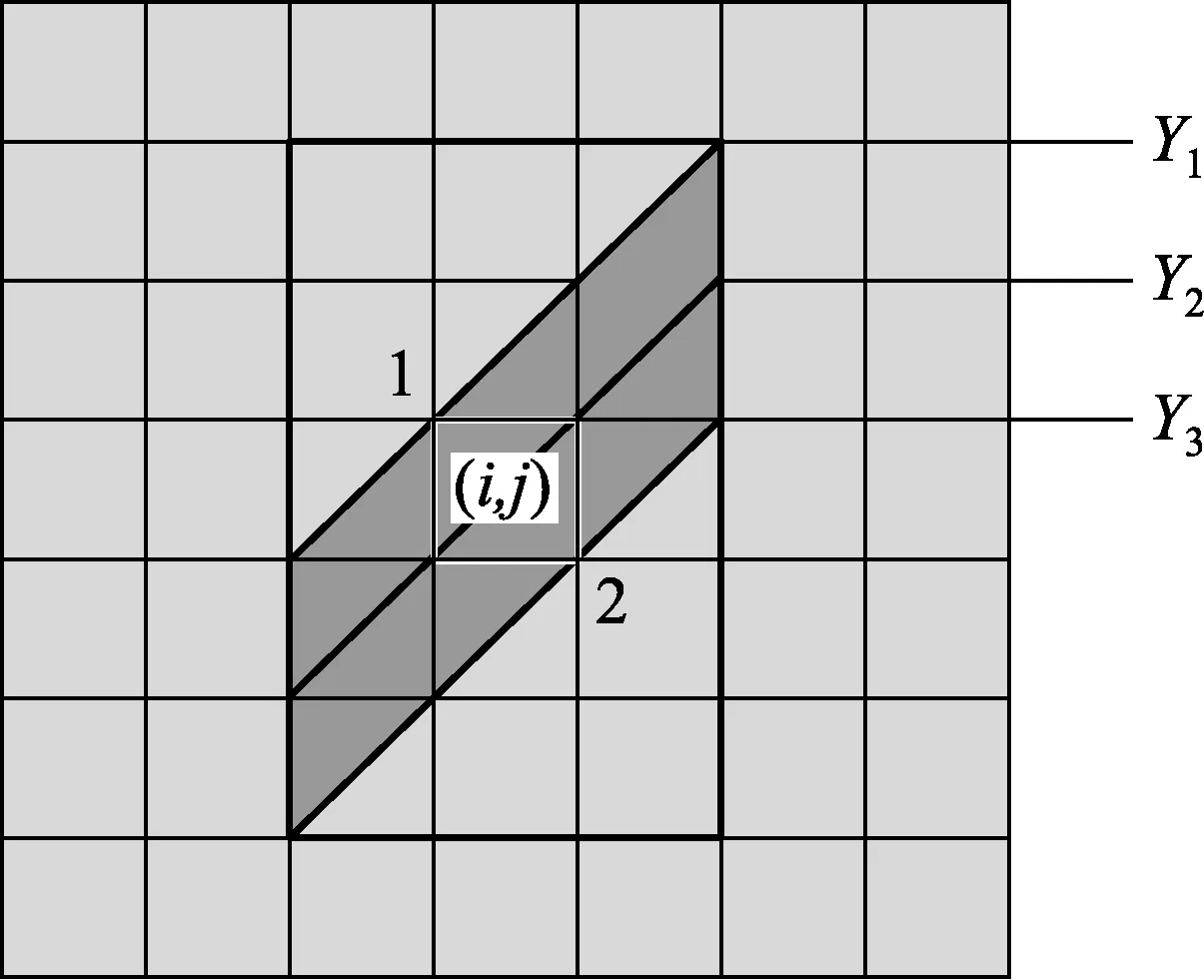
图2 直线可能扫过的像素范围

把在原图像中截取的一个像素(i,j)为中心的5×3像素矩阵(记为F)作为研究对象,来计算所设直线的参数,如图3所示。

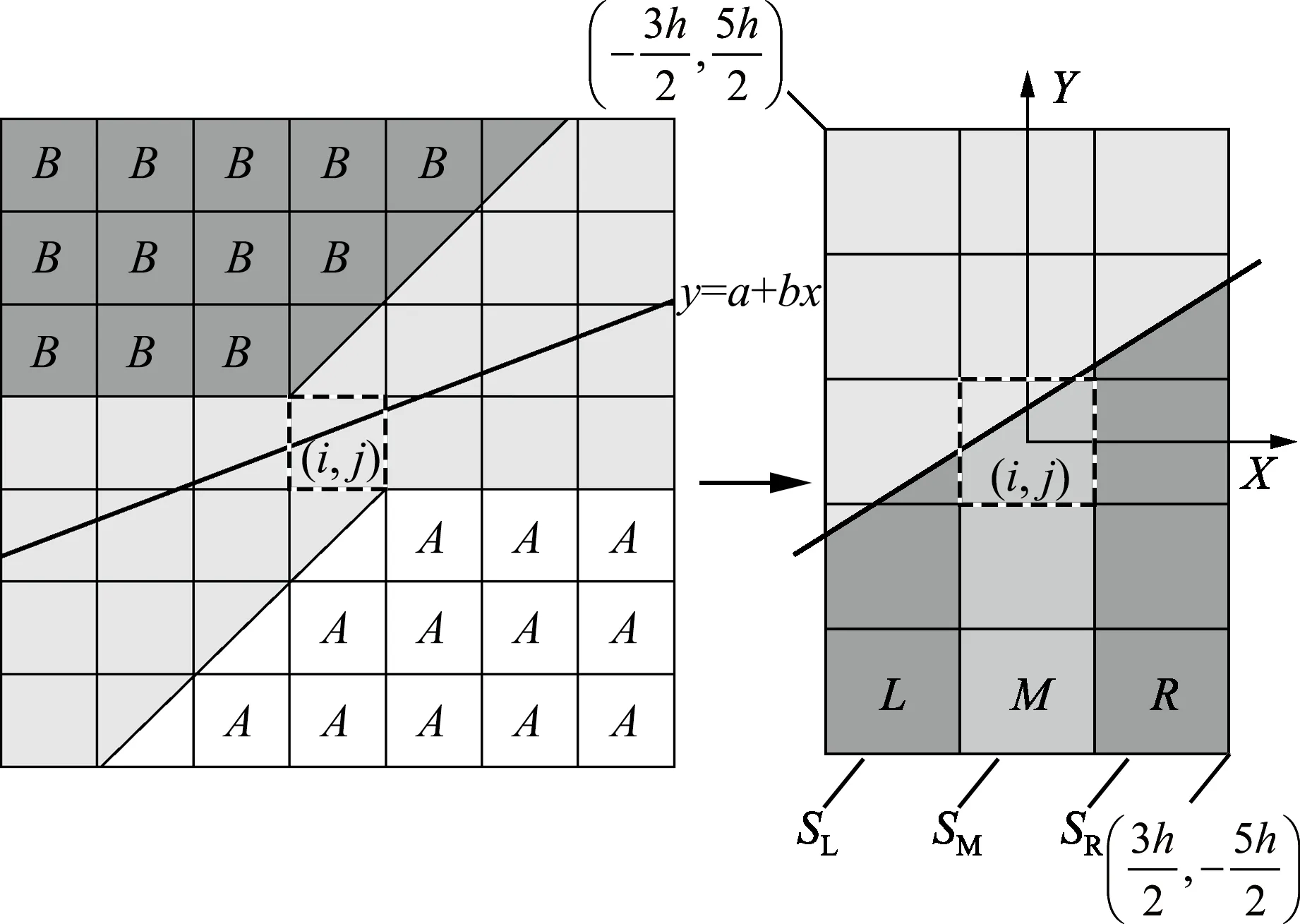
图3 求解直线方程参数的图示

图3中,以像素(i,j)(虚线框所示)中心为坐标原点建立如图3右侧所示的直角坐标系[8]。

像素(i,j)的灰度值应满足:

(3)

式中:A,B为像素内边缘两侧的灰度值;h为正方形像素的边长;Si,j为像素(i,j)位于边缘直线y=ax+b下方的面积(0≤Si,j≤h2)。

令SL,SM,SR分别代表矩阵中左、中、右3列像素中每列像素的灰度值之和,则有:

(4)

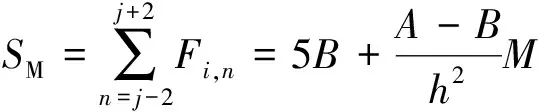
(5)

(6)

式中:L,M,R分别代表每列像素中位于边缘直线下方的面积。L,M,R满足:

(7)

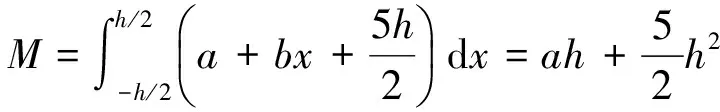
(8)

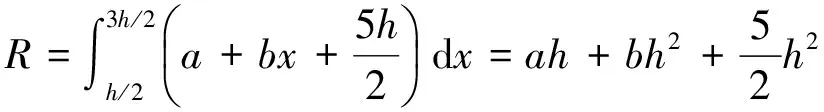
(9)

联立式(5)与式(8)可得:

(10)

联立式(4)、式(6)、式(7)、式(9)可得:

(11)

式(11)中A和B的值是未知的。因为实际中一个像素内并不存在A和B两种灰度值,所以A和B的值应由该像素邻近的几个像素的灰度统计值估计得到。此外,采用矩阵F中哪几个像素计算该估计值与边缘直线斜率的正负性有关,故在此依据b的正负分别讨论。

当b∈[0,1]时,所选取的像素如图4(a)的虚线框所示。因为与中心像素的距离不同,各像素的灰度值对中心像素最终灰度值的贡献也不同。根据待处理图像的成像质量选取适当的标准差σ(主要受对焦情况的影响)建立高斯函数,如式(12)计算各像素所具有的权值,分别记为α,β,γ。

G(u,v)=Ce-(u2+v2)/(2σ2)

(12)

式中:u和v分别为各像素距中心像素的坐标距离;C为归一化系数。设α>β>r,则A和B的计算公式为:

A=βFi,j+2+γFi+1,j+2+αFi+1,j+1

(13)

B=βFi,j-2+γFi-1,j-2+αFi-1,j-1

(14)

同理,当b∈[-1,0]时,由图4(b)可得到

A=βFi,j+2+γFi-1,j+2+αFi-1,j+1

(15)

B=βFi,j-2+γFi+1,j-2+αFi+1,j-1

(16)

综上,对于边缘的斜率b∈[-1,1]的情况,给出更加一般化的计算A和B的表达式:

A=βFi,j+2+γFi+m,j+2+αFi+m,j+1

(17)

B=βFi,j-2+γFi-m,j-2+αFi-m,j-1

(18)

其中m满足以下等式:

(19)

图4 计算A和B时选取像素的情况

2.2 |fc|>|fr|的情况

由|fc|>|fr|可知,此时边缘直线的斜率b满足|b|>1。故在这种情况下应在原图像中截取以像素(i,j)为中心的3×5的像素矩阵,并从上到下依次计算矩阵内每行像素的灰度值之和,分别作为SR,SM,SL值。同时在原坐标系保持不变的情况下,将所设的边缘直线的方程改为x=a+by。做上述处理后,参数a和b的求值表达式不变。此时A和B的值由式(20)、(21)给出,其中m同式(19)。

A=βFi+2,j+γFi+2,j+m+αFi+1,j+m

(20)

B=βFi-2,j+γFi-2,j-m+αFi-1,j-m

(21)

综上,根据原图像信息求出中间变量SR,SM,SL以及A,B之后,将其代入式(10)和式(11)就可以得到边缘直线方程的参数。

2.3 亚像素边缘位置的求取

首先,求出边缘在该像素的梯度:

(22)

其次,求出过原点、且方向向量与N相同的直线和已知边缘直线的交点,记为(x,y),则像素(i,j)的亚像素边缘位置为:

(23)

式中x与y的符号不同。这是因为求解边缘直线时所建立的坐标系的X轴与图像坐标系的i轴(即列坐标轴)方向相同,而Y轴与j轴(即行坐标轴)方向相反。

在这种情况下,按本文的求取方式则得到的边缘亚像素位置为S2。若直接采用直线的截距计算,则得到的边缘亚像素位置为S1。由图5可知,此时该位置已不在像素内。这说明本文将边缘的斜率考虑在内来计算边缘的亚像素位置更加合理。

图5 亚像素位置的选取方式

3 实验结果及分析

图6 实验所使用的进气歧管图

本文使用的汽车发动机进气歧管如图6(a)所示。在工程实践中通常先对标准件进行检测得到参考值,然后再对实际生产的零件进行检测,最后将检测结果与参考值进行对比,从而判断生产的零件是否合格。本文以规格分别为50.00 mm×40.00 mm和50.05 mm×40.05 mm的2种标准件作为检测对象。图6(b)是规格为50.05 mm×40.05 mm的标准件图像。为保证算法的重复性,实验时拍摄多组零件的图像,其中每组零件的图像是零件在同一位置连续拍摄多张得到的。实际生产时主要测量该零件的2种尺寸:长轴和短轴。为了验证本文算法的有效性,本实验同时还采用了文献[8]的方法和文献[10]所介绍的曲面拟合方法对该零件的图像进行亚像素边缘检测,并计算2个待测量的像素尺寸。表1从标准差、最大偏差、最小偏差3方面给出了实验数据的统计结果。其中,标准差是用各组测量数据按式(24)计算得出的, 用以表征检测结果的精度。

(24)

式中:μ为各组数据的均值;N为样本数。最大偏差和最小偏差分别为各测量数据与其组均值偏差的绝对值的最大和最小值,用来表征各组测量数据中的奇异值。

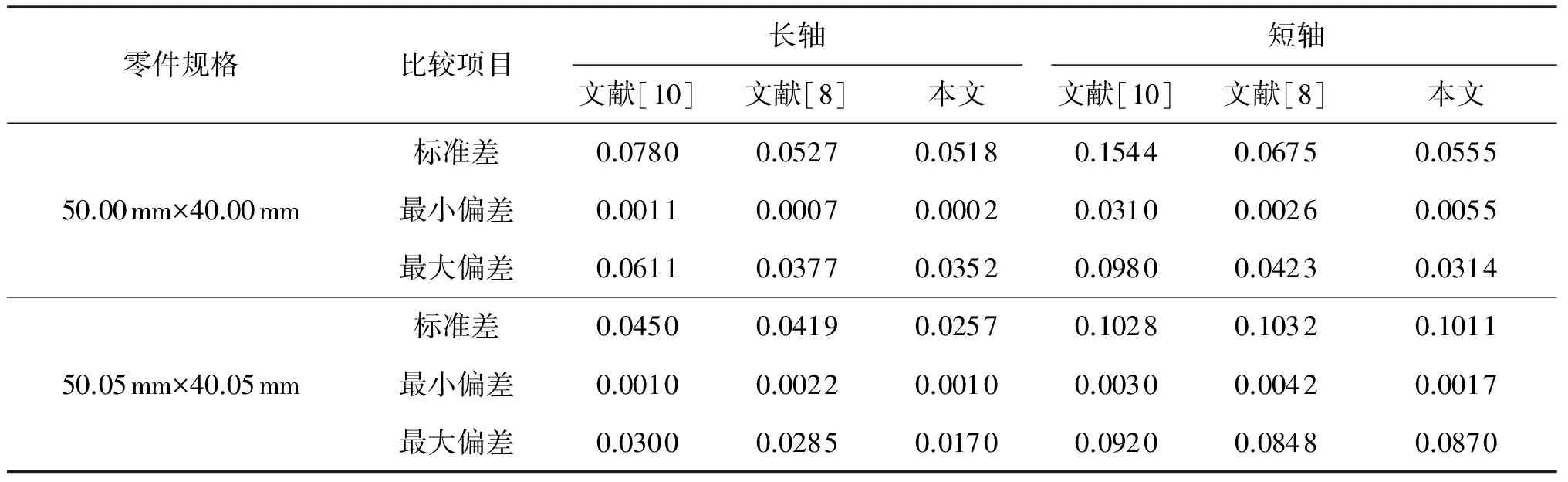
表1 长轴和短轴实验数据的统计结果 像素

由表1可知,本文方法的标准差、最小偏差和最大偏差都要小于文献[8]和[10]的方法,即本文方法的准确度要高于文献[10]和[8]的方法。以标准差的降低率为例,具体数值见表2。

表2 本文方法与文献[10]和[8]的比较 (%)

图7给出了采用文献[10]所介绍的曲面拟合方法和本文方法,对进气歧管进行亚像素边缘检测所得到结果的4个部位的局部对比图,分别用数字1～4编号。其中深色线为曲面拟合方法的检测结果,浅色线为本文方法的检测结果。由编号为3和4的局部对比图可知,在相同位置上,曲面拟合方法会出现检测到多条边缘的情况,而本文的方法没有出现这种情况。这说明本文方法符合文献[11]所述的优良边缘检测算子应具备的单边缘响应准则。

图7 本文方法和曲面拟合法边缘检测结果局部对比图

4 结 论

本文针对汽车发动机进气歧管,提出了一种基于边缘像素投影的亚像素边缘检测方法。通过分析边缘投影对其所穿过的像素的灰度值的影响效应,建立了灰度值的面积加权计算模型,然后利用边缘像素的某一邻域内的灰度值计算出表示边缘投影的曲线方程,进而求得边缘的亚像素位置。对规格分别为50.00 mm×40.00 mm和50.05 mm×40.05 mm的汽车进气歧管长短轴进行检测实验,实验结果表明,与文献[8]基于曲面拟合的亚像素边缘检测方法相比,长短轴标准差分别降低了1.71%和17.78%,以及38.66%和2.03%。本文提出的亚像素边缘检测方法,不仅准确度高,而且能够避免在有较多干扰时的多重响应。

[参考文献]

[1] 伍济钢. 薄片零件尺寸机器视觉检测系统关键技术研究[D]. 武汉:华中科技大学, 2008:2-10.

[2] 祝宏, 曾祥进. Zernike 矩和最小二乘椭圆拟合的亚像素边缘提取[J]. 计算机工程与应用, 2011, 47(17):148-150.

[3] 段振云,王宁,赵文辉,等.基于高斯积分曲线拟合的亚像素边缘提取算法[J]. 计量学报，2016,37(4):371-374.

[4] Devernay F. A Non-Maxima Suppression Method for Edge Detection with Sub-Pixel Accuracy[C]// Rapport De Rechercheinstitut National De Recherche En Informatique Et En Automatique,1995. https://doi.org/10.1.1.35.1863.

[5] Rockett P. The accuracy of sub-pixel localisation in the canny edge detector[C]// Proc. of the British Machine Vision Conference. BMVC 1999:392-401.

[6] Hermosilla T, Bermejo E, Balaguer A,etal. Non-linear fourth-order image interpolation for subpixel edge detection and localization[J].ImageVisionComput, 2008,26(9):1240-1248.

[7] Tan J B, Ao L, Cui J W,etal. Subpixel edge location based on orthogonal Fourier-Mellin moments[J].ImageandVisionComputing, 2008, 26(4): 563-569.

[8] Trujillo-Pino A, Krissian K. Accurate subpixel edge location based on partial area effect [J].ImageandVisionComputing, 2013, 31(1):72-80.

[9] 张爱丽,佟首峰,韩成. 基于CCD的光斑能量分布测量及特性分析[J]. 激光与红外, 2011, 41(6):622-626.

[10] Steger C. 机器视觉算法与应用[M]. 杨少荣, 吴迪靖, 段德山, 译. 北京:清华大学出版社, 2008.

[11] Canny J. A computational approach to edge detection[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,1986, 8(6):679-698.