粗大误差判定准则在靶场试验数据预处理中的应用
刘艳,于露
(91550部队,大连 116023)
由于靶场飞行器飞行试验测量数据的获得来之不易,试验数据处理和分析成为整个飞行器飞行试验重要的环节之一。在飞行器飞行试验测量中,测量误差的来源主要包括测量方法误差、设备误差、环境误差和人员误差等。多种原因造成了测量数据中包含某些错误观测量。工程中通常将测量误差分为三类,即系统误差、随机误差和粗大误差[1]。对于不同的类型误差,有不同的误差特性和不同的数据特性,采用不同的数据处理方法。粗大误差是指量值比较大的误差,可能由于某些突发性异常因素造成,也可能由于人为因素或是其它未知因素造成[2]。粗大误差的存在显著歪曲了测量结果,影响测量结果的准确性和可靠性。试验数据进行预处理目的是剔除粗大误差[3]。由于到目前为止,还没有适合靶场各种复杂条件下统一的粗大误差判定准则,急需的实时数据处理需要快速进行粗大误差的判定,粗大误差判定准则如何在靶场数据处理中得到应用,需要对常用的四种粗大误差判定准则应用特点进行分析。寻求不同数据使用要求下粗大误差的判定方法,旨在利用试验测量数据对被试飞行器的性能做出合理的鉴定,为飞行器改进设计、装备定型和部队使用提供结论性意见。
1 试验数据预处理的方法
试验数据测量粗差是指一组试验测量数据中,明显偏离正常值的那些值,通常表现为脱离绝大多数数据点,数值相差悬殊、离散出现、数量不多,也称为跳点、野值[4]。粗差会严重影响测量结果的真实性,需要滤除。从工程应用的角度,可将粗差分为二类,即粗差单点和粗差群点。试验数据预处理的方法是对某一组试验数据进行粗差判定,剔除奇异数据,对相应的原始数据进行内插处理和曲线拟合,最终确定参加统计的试验数据[5]。实际工程应用中,粗大误差的判定与剔除必须慎之又慎。需结合粗大误差的判定准则,认真分析可疑数据的产生原因,可以通过粗大误差判定的原则进一步初步判定;通过粗大误差判定的准则进行异常值的剔除。
1.1 粗大误差判定的原则
粗差的判定首先建立在对其正确判别的基础上。要求对测量方法、测量过程有较好的了解和认识,应掌握与被判别参数有密切联系、发生关联动作和变化的其它参数的情况[6]。在判断是否为粗差时应该遵循以下原则:
a.明显偏离其它测量值的那个值可能仅仅是数据中固有的随机变异性的极端表现,若此值与其它属于同一个总体,不是异常值,若此值与其它不属于同一个总体,则该值是异常值,确定为粗差。
b.当试验者清楚地知道试验条件已经变化,不管它是否与其它测量值一致都属于异常值,确定为粗差。
c.当清楚地知道该值是在不同的固有因素作用下发生的,如果能够确信可疑数据属于物理或技术操作等因素引起的粗大误差,则可以将其直接剔除不用,则按异常值剔除。
d.当在试验条件下,明显偏离其它值的原因不清楚时,必须使用判定准则进行推断。粗差的判定关键是构造合适的统计量,并求出它的分布。
1.2 粗大误差单点判定的准则
常用的四种对正态或近似正态分布的样本重复测量数据异常值判定准则有拉依达准则(3б准则)、格拉布斯准则(极值偏差法)、狄克逊准则(极差比法)、肖维勒准则[7]。常采用3б(б—标准偏差)准则或根据误差曲线直观判定某一数据是否为异常值,还可采用极值偏差法和极差比法。
1.2.1 拉依达准则
拉依达准则又称3б准则,以测量次数充分大为前提。在样本n≤10的情形下,用3б准则剔除异常值是失效的[8]。假设某一测量参数有N个测量值为xi:i=1,2,3…N,其均值和方差分别为μ,б2,若Xd满足(1)式,判定Xd为粗差。

其中:μ—均值;σ—标准偏差;Xd—粗差可疑数据。
1.2.2 格拉布斯准则
格拉布斯准则又称极值偏差法,以小子样为前提。
a.在σ和μ(μ—均值)未知的条件下,判定可疑结果的观测值是否为异常值。已知样本值X1、X2、…、Xn及总体标准差σ,将样本值按从小到大的顺序排列得X(1)≤X(2)≤…≤X(n),视X(n)(或X(1))为可疑,构造统计量Gn(G1)的值:
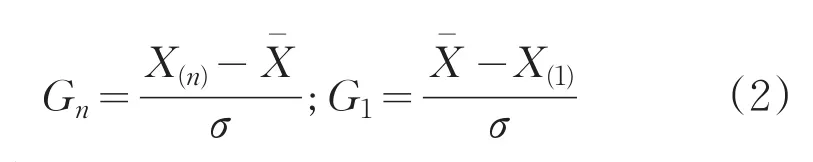
其中:μ—均值;σ—标准偏差;X(n)或X(1)—粗差可疑数据
b.给出显著水平,显著性水平一般取0.01或0.05,由α和样本数n查格拉布斯准则判据取值表T(n,α)如表1所示。若Gn>T(n,α),则判定xn为异常值;若G1>T(n,α),则判定x1为异常值。

表1 格拉布斯准则判据取值表T(n,α)
1.2.3 狄克逊准则
狄克逊准则又称极差比法。已知样本值x1、x2、…、xn,将样本值按从小到大的顺序排列得x(1)≤x(2)≤…≤x(n),计算统计量(Dixon统计量)rij的值,此种统计量有以下四个:
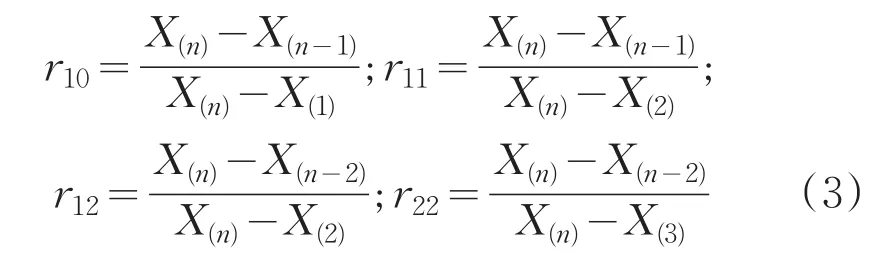
根据随机模拟结果,一般认为:3≤n≤7时以使用r10为佳;8≤n≤10时以使用r11佳;11≤n≤13时以使用r21为佳;14≤n≤30时以使用r22为佳;给出显著水平α,查狄克逊准则判据取值表D(n,α)表,如表2所示。若rij>D(n,α),则认为x(n)(或x(1))为异常值,应予于剔除。若rij≤D(n,α),则无理由认为x(n)(或x(1))为异常值,应予以保留。
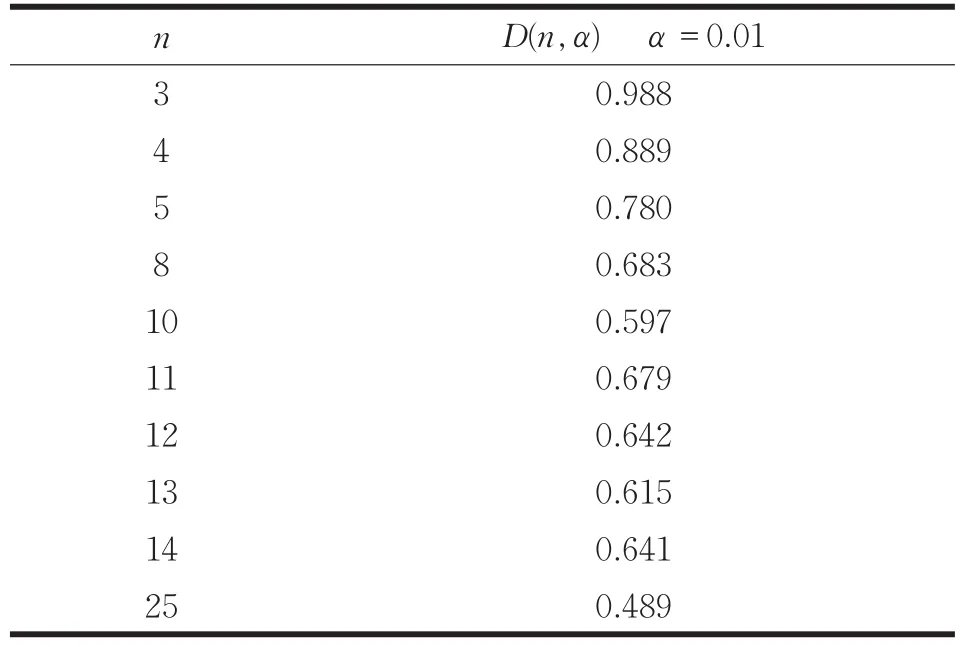
表2 狄克逊准则判据取值表D(n,α)
1.2.4 肖维勒准则
肖维勒准则以正态分布为前提。假设某一测量参数n个测量值为Xi:i=1,2,3…N,其均值和方差分别为μ,σ2,若Xd满足(4)式,判定Xd为粗差。
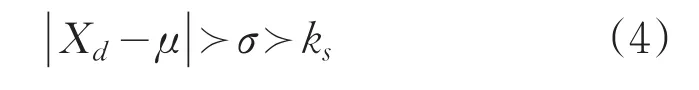
其中:μ—均值;Xd—粗差可疑数据;σ—标准偏差;ks—肖维勒判据。肖维勒准则判据取值表如表3所示。
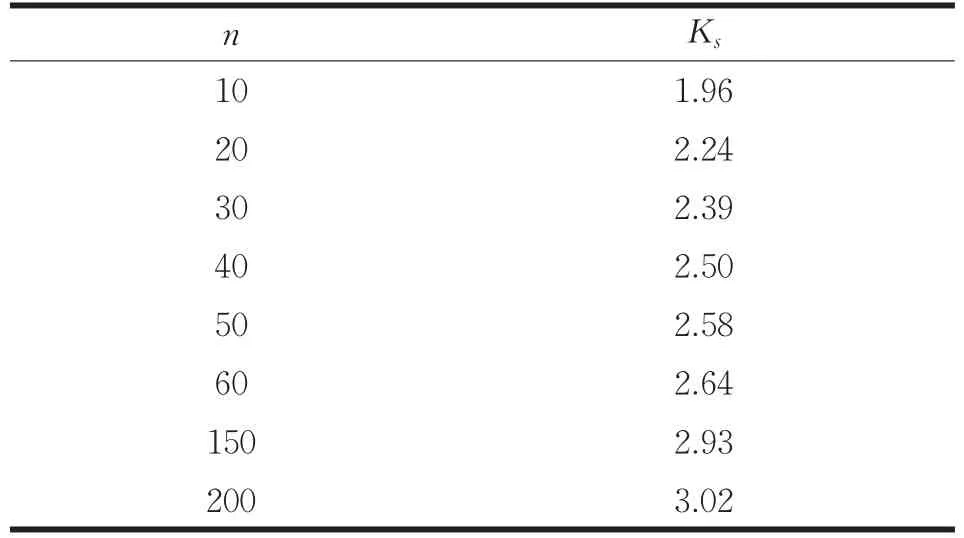
表3 肖维勒准则判据取值表
2 实际应用及特点分析
在实际的数据处理工作中,为了便于说明,以粗差的单点处理方法进行计算分析。为了进一步说明各种粗差判定准则的特点及应用时机,以某型飞行器距离跟踪精度试验测量分量为例,3000个子样测量计算均值为0.929m;测量标准偏差为3.025m。测量精度指标为1m,取其中25个样本小段测量数据,进行异常值判定分析。分别用四种粗大误差判定准则进行计算分析。
2.1 应用举例
在某型飞行器某次飞行试验中,按样本的数从小到大的顺序排列,测量残差数据表如表4所示,其中n为样本数,Δ(m)为测量残差。

表4 测量残差数据表
从测量数据表4中可知n=25时,X(25)=10m,残差最大,可能为异常值,分别用四种方法进行判别。
2.1.1 拉依达准则法
由于测量均值μ为0.929m,标准偏差σ为3.025m。根据公式(1)计算10m>3σ=9.075m,由拉依达准则,可判断其为异常值,应予以剔除。
2.1.2 格拉布斯准则法
根据公式(2)计算G(25)=2.999。给出显著水平α=0.01,n=25查表1,格拉布斯准则判据取值T(0.01,25)=3.01因为G(25)<T(0.01,25),不能判定X(25)=10为异常值,应予以保留。
2.1.3 狄克逊准则法
当n=25,使用r22为佳。根据公式(3)计算r22为0.473。给出显著水平α=0.01,n=25查表2,狄克逊准则判据取值临界值D(n,α)=0.489,r22<rα,无理由认为X(25)为异常值,应予以保留。
2.1.4 肖维勒准则法
当n=25,查表3,肖维涅判据取值ks为2.39,标准偏差σ为3.025,误差值X(25)=10,根据公式(4),满足公式要求,确定此值为粗差,应予以剔除。
2.2 特点分析
从以上四种检验方法计算中可以看出:对于这组数据中的最大值是否为异常值的判定,用拉依达准则法和肖维勒准则法可以检查出其为异常值,而格拉布斯准则法和狄克逊准则法未能检验出为异常值。如表5所示。

表5 四种检验方法分析表
通过检验方法的分析,可以看到:
所有的异常值判别准则都是以数据正态分布为前提,因此它们的应用也有其局限性,大样本用拉依达准则最为简单;肖维勒准则法计算比较简单,计算的准确度有些粗糙,适合快速判定。小样本用拉依达准则通常是失效的。格拉布斯准则和狄克逊准则都能得出严格的结果,格拉布斯准则适用于剔除一个异常值;狄克逊准则适用于剔除多个异常值。在靶场的试验数据预处理过程中,由于存在实时和事后数据预处理工作,实时数据预处理要求提供快速判定数据,因此,对靶场数据预处理工作应遵循以下原则:
(1)由于3σ计算简便易行,应首先采用3σ法对给定的数据进行第一次异常值的判定及剔除;肖维勒法简单直接,计算简单,可用于现场判断,但方法粗糙,可结合3σ法综合判定。
(2)狄克逊准则无需计算算术平均值和标准差,方法比较简单,该准则当目测估计有多个异常值时,建议使用狄克逊准则。狄克逊准则法只使用部分数据,可用于现场判断。采用的信息越多,异常值的判定就越准确。
(3)格拉布斯准则法比较精确地计算出某一怀疑值为异常值,由于受到n的限制,因此,在小样本情况,可对数据进行第二次异常值的判定及剔除。
3 结束语
靶场试验数据的预处理是对单套测量设备的测量数据进行单独加工处理的过程。粗大误差的判定不能单独使用一种判定准则进行异常值剔除,整个处理过程是一个反复加工的过程,需要根据靶场实时和事后数据处理要求综合四种判定准则联合应用。通过对试验数据预处理方法的分析,采用合理的粗差判定方法,鉴别和剔除异常值,利用模型和插值方法对剔除点进行补点。使有限的外场试验数据,得到更加充分、合理地利用。在某次动态飞行试验数据处理中,应用该数据预处理分析方法,对试验数据进行预处理分析,减少了测量误差,用实例验证了靶场试验数据预处理四种准则应用的合理性和有效性。科学、有效地对飞行试验的测量结果进行了数据处理和分析。试验数据预处理方法的研究,进一步完善靶场试验数据处理的方法,保证最终结论的准确性。
[1]于晓峰.装备试验数据处理[M].北京;国防工业出版社,2010:1-15.
[2]刘小会.正态分布积分的高精度算法[J].长春理工大学学报:自然科学版,2011,34(03):179-181.
[3]肖洋,李平,王鹏,等.基于最小方差的自适应K-均值初始化方法[J].长春理工大学学报:自然科学版,2015,38(05):140-144+149.
[4]王鹏,王健安,郭畅,等.基于云计算及数据挖掘技术的海量数据处理研究[J].长春理工大学学报:自然科学版,2013,36(06):157-160.
[5]沈凯,吴胜昔,彭竹,等.基于改进残差的显著误差检测方法[J].华东理工大学学报:自然科学版,2014,40(06):730-734.
[6]洪进,张立中,王霞.动态靶标误差建模分析[J].长春理工大学学报:自然科学版,2014,37(05):69-72.
[7]欧阳琳男.粗大误差判断准则运用条件的相关分析[J].中国计量,2017(11):106-107.
[8]韩旭,王建宇,祖先锋.基于时间序列模型的系统最大值指标评定方法[J].系统工程与电子技术,2012,34(04):839-645.

