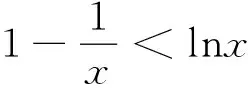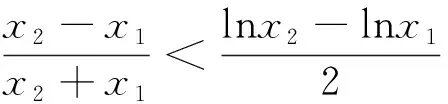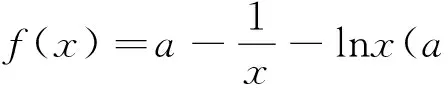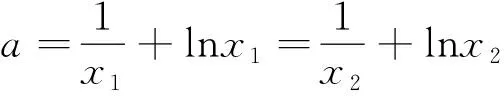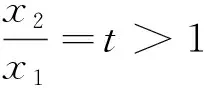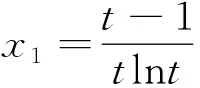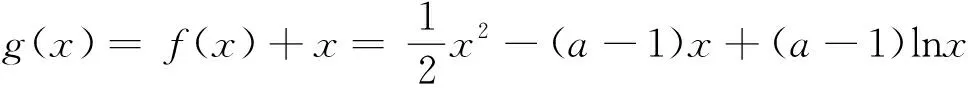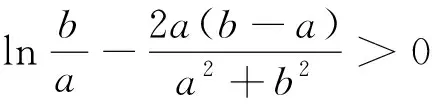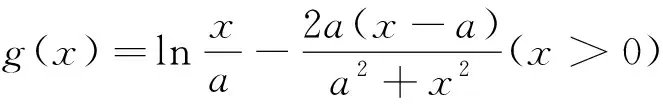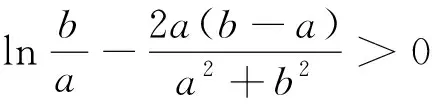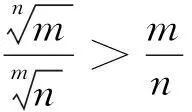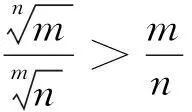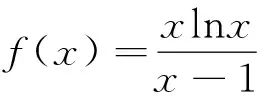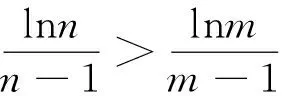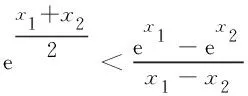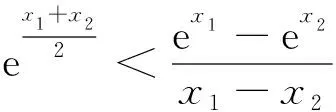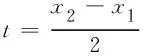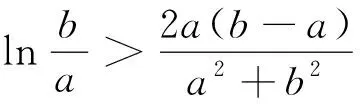例谈导数视角下“构造函数证明不等式问题”的解决策略

江苏省南京市第九中学

竺宝林 (邮编：210018)

现行高中教材中，导数已成为研究函数性质的一种重要工具.在新课程背景下，不等式的证明已大幅度降低要求，但是不等式证明中蕴含着丰富的数学思想与数学方法，各类考试特别是高考压轴题位置依然会出现不等式证明问题，只是用纯不等式的方法解决不等式证明已不多见，一般情况都需要利用转化与化归思想，转化为函数，进而通过求导，进一步转化为函数的单调性、极值、最值来解决.在解决这类问题时，往往需要先构造函数.因而，函数的变化与构造成为分析与思考此类问题的难点.本文通过对实例的分析，与大家探讨此类问题的各种类型与解决策略，不当之处，敬请斧正.

策略1直接作差，构造函数

例1求证：lnx≤x-1.

分析考虑直接作差构造函数.

当00，f(x)单调递增；当x>1时，f′(x)<0，f(x)单调递减.

所以fmax(x)=f(1)=0，f(x)≤f(1)=0，即lnx≤x-1.

评注此不等式是很多复杂不等式证明的基础，其几何意义是函数y=lnx的图象在点(1,0)处的切线y=x-1在函数图象之上(切点除外).

策略2先等价变形，再作差构造函数

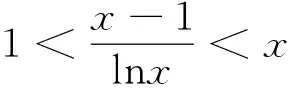
分析可以把不等式作等价变形后再构造函数.

解答因x>1，所以lnx>0，只要证lnx

而lnx

令g(x)=xlnx-x+1，则g′(x)=lnx，当x>1时，g′(x)>0.

所以g(x)在(1,+∞)内单调递增，则g(x)>g(1)=0，即x-1

策略3利用齐次式消元，构造函数

则f(t)在(1,+∞)内单调递减，得f(t)

求证：f′(x1)+f′(x2)<0．

两式相减，得

.

因

评注消元是解决本类问题的主思想，构建齐次式是关键，首先把式子化简成只含有x1、x2，若是关于x1、x2的齐次式，就能通过此方法达到构造函数的目的.

策略4利用非齐次式消元，构造函数

评注非齐次式依然可以先消元再构造，只是注意其与例3、例4的区别.

策略5利用结构对称，构造函数

评注例3、例4、例5侧重于消元，而这两题更侧重于式子两边的形式结构的对称，利用对称性构造函数.

策略6利用主元思想，构造函数

，

当x>a时，g′(x)>0，则g(x)在(a,+∞)内单调递增，由0g(a)=0，

策略7先指数化对数，再构造函数

当x∈(1,+∞)时，g′(x)>0，则g(x)在(1,+∞)内是增函数.

故g(x)在x=1处取得最小值g(1)=0，所以g(x)≥g(1)=0，即x-1-lnx≥0，所以f′(x)≥0，f(x)在(1,+∞)内是增函数，因为n>m>1，则f(n)>f(m)，

mnlnn-nlnn>mnlnm-mlnm，

即mnlnn+mlnm>mnlnm+nlnn.

则lnnmn+lnmm>lnmmn+lnnn，

评注原式是幂的关系与乘除运算，直接构造函数并不可取，若两边同时取对数将原式转化为加减运算，进而构造相应的对数函数会使问题迎刃而解，是一种不错转化问题的思路.实际上，当初数学家引入对数的目的之一就是为了把复杂的幂的运算转化为加减运算.

策略8利用常见不等式放缩后构造

所以g′(t)=2e2t-2tet-2et2et(et-t-1).

设h(t)=et-t-1，h′(t)=et-1，当t>0时，h′(t)=et-1>0恒成立，h(t)递增，

则h(t)>h(0)=0，则g′(t)>0恒成立，所以g(t)递增，则g(t)>g(0)=0，

即e2t-2t·et-1>0(t>0)恒成立，所以命题得证.

评注放缩法是高中数学中重要的方法之一，主要在不等式中运用.随着不等式在高考中要求降低，放缩法在渐渐失去了原来的地位.但是，高考数学历来重视数学思想、数学方法的考查，放缩法在高考中仍有其存在的空间.

在证明不等式时，通常需要根据不等式的特点，进行构造函数，用导数研究函数的性质，从而达到证明不等式的目的，即把证明不等式转化为用导数解决的函数问题.此类问题变化多、思路多、方法多，但是核心问题点在于构造函数，具有一定的创造性和隐蔽性，需要熟悉常见构造策略，具体解决时，需要通过对题目中条件的转化、变量的增减、结构的改造进行多方位的分析与思考.

1 马金仙.两道经典不等式的讲评历程[J].数学通讯(下半月)，2016(7)

2 程爱文.让学生的心灵去旅行——一堂试卷讲评课教学[J].数学通讯(下半月)，2011(8)