文化色彩：数学课堂的润滑剂

安徽省合肥市第十七中学

夏怀东 (邮编：230022)

数学新课标指出：“数学文化是指数学的思想、精神、语言、方法、观点，以及它们的形成与发展，还包括数学在人类生活、科学技术、社会发展中的贡献和意义，以及与数学相关的人文活动.”应该说，数学课堂是渗透数学文化的主阵地、主渠道，是践行“让学生体会数学的文化价值”的重要途径之一. 实践表明，文化色彩是数学课堂的润滑剂，它能使数学课堂克服枯燥，充满生机与活力.下面从四个方面谈谈“文化色彩”在数学课堂中的运用.

1 新课导入中的文化色彩

数学核心素养中的“直观想象”和“数学抽象”告诉我们，数学中抽象概念的引入既离不开直观、形象、鲜明的具体问题的支撑，又离不开数学抽象的环节.因此，新课引入时，要注意创设两种情境：情感情境与思维情境.良好的情感情境，能调动学生情感的积极参与，很快进入课堂状态. 良好的思维情境，能调动学生思维的参与，主动思考与新课有关的问题.

比如，学习指数函数概念时，我用两例引入: (1) 我国古代著名的思想家庄子在《庄子·天下篇》中写道：“一尺之棰，日取其半，万世不竭”.设取x天之后，剩下y,则y与x的函数关系式是______；(2)假设你今天的数学水平是1，以后每天比前一天增加1%，则经过x天之后，你的数学水平y与x之间的函数关系式是______.

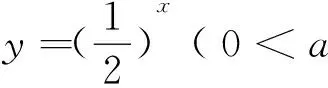
又比如, 正弦曲线的起始课教学, 从提问学生开始:

师: 如图的表格是钱塘江的潮高在相应时间内的数据，你能知道潮高的变化趋势吗？

生: 从数据上看不出来，可以画图吗？

师: 想法不错，你准备怎样作图？

生: 要建立坐标系才行，以横轴代表日期，纵轴代表潮高，描出对应的点.

师: 很好, 从这些点的位置，你发现了什么？

生: 我来连连线，似乎此起彼伏，很美呀！

师: 完全正确，它就是下面的一条美丽的曲线！这正是本节课我们要研究的正弦曲线.

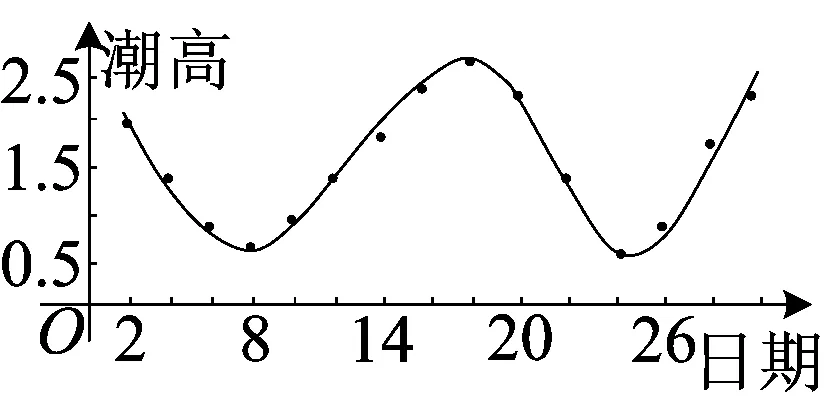
“数据分析”也是数学核心素养之一.从学生熟悉的现实生活中的数量对应关系引入新课，表格与图象联系、数量与坐标联系、趋势与图形联系，并与前期学到的模拟函数紧密结合，既让学生体会数学的文化性，又让学生学会数据处理、数据分析的方法.如果我们经常这样引入新课，学生学习数学的热情必然增加.

2 教学新知中的文化色彩

在绝大多数学生的心目中，数学是单调枯燥的，数学是难的，数学是不易理解的，数学是游离于现实生活和人文科学之外的东西.为此，在数学新知教学中，教师要善于举例，即多用学生熟悉的、直观的、形象的现实文化背景来解释、说明、印证过于形式化的数学定理、公式和性质等等，这样既可以加深学生对数学规律、数学方法和数学思想的理解与把握，又能使他们深切感受到数学就在我们的身边、就在我们的生活中,从而有效培养学生的人文意识、提高课堂温度.

比如，在教学数学公理“折线段长永远大于直线段长”时，这样设计：

师：在高中日常教学中，我们遵循的路径往往就是直线段——“从学习到高考”，如图所示. 直奔主题、直奔目标，活动可以不要，阅读可以不要，升旗做操可以不要，卫生可以不要，文明规范可以不要，团结合作可以不要，等等，这样下去，学生的人格会健全吗，将来怎样独立生活呢？大家思考一下，通往高考的路应该怎么走？

生：走折线吧：

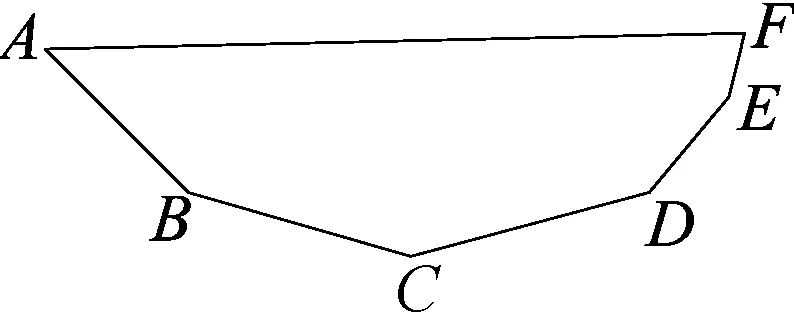
师：同学们发现了什么？

生：折线ABCDEF的长度大于直线段AF的长度.

师：完全正确.将学习和活动相结合、学习和做人相结合、学习和实践相结合、学习和规范相结合、学习和感恩相结合、学习和精神相结合，能从中接受多种教育，不仅高考能取得优异成绩，而且能全方位得到锻炼和成长.因此，我们倡导通往高考的路沿折线段走.

师：数学公理告诉我们，“折线段长永远大于直线段长”.将数学运用于教育科学，既直观、形象、鲜明，又能使教育科学更加完善——数学的力量所在！

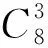
鲜活的例证，让抽象的数学结论变得直观、生动、形象.“班干值日”和“检验产品”中还蕴含着数学,同学们感受深刻,公式铭刻于心, 突破了教学难点.

3 例题讲评中的文化色彩

数学是思维的体操, 思维能力是数学能力的核心. 为此,新课标指出：“数学教学要注重提高学生的数学思维能力.” 因此, 例题讲评中应根据教学内容适当选择有层次、有坡度、有力度的问题让学生思考、分析和探究，着力提高学生的数学思维能力.

一般地，例题讲评有三个层次，可以用摘桃子来比喻：第一层次，基础题，只要愿意伸手就能摘到桃子，思维层次较低.第二层次，中档题，跳一下可以摘到桃子，思维层次适中.第三层次，较难题，多跳几下摘到桃子，思维层次较高.

比如，在古典概型例题讲评中，设计下列题组：

(1)设a,b∈0,1,2,3,4,求|a-b|≤1的概率.

(2)设a,b∈1,2,3,4,5,6,7,8,9,求|a-b|≤1的概率.

(3) 我们知道，“心有灵犀”一般是对人的心理活动非常融洽的一种描述，它也可以用数学来定义：甲、乙两人都在{0，1,2,3,4,5,6，7,8,9}中说一个数，甲说的数记为a,乙说的数记为b,若a-b≤1,则称甲、乙两人“心有灵犀”.求甲、乙两人“心有灵犀”的概率.

给出的三个题目，符合思维由浅入深、由易到难、层层递进的原则.第(1)题数据少，可以尝试逐个确定基本事件总数和有利于a-b≤1的基本事件数，属于基础题.第(2)题数据增多，逐个确定比较复杂，可以借助第(1)题的经验和规律处理，属于中档题.第(3)题是将第(1)题、第(2)题整合，并加上新颖的背景，形成一道概率文化题，属于较难题.人的心理活动还能用数学来刻划, 学生感到很新鲜，探究的欲望油然而生.通过主动地阅读、理解、迁移新定义, 快速实现解题目标,学生意犹未尽, 脸上露出甜美的微笑——数学与人文的完美结合!

又比如，“导数在实际优化问题中的应用”例题讲评课，先用文化题引入：

如图，有一条河流，河宽AB=30米，武警战士在离B点60米处的C点发现河对岸A点处有人掉入水中，立即前往营救.已知武警战士在河岸上的跑步速度为6米/秒，在河水中游泳的速度为2米/秒，试问武警战士最快能用几秒赶到？

初看起来，这是一道现实生活问题，尝试数学建模处理：是最值问题，建立函数模型.

数学文化常常表现在“实际问题数学化”中—— 用数学的眼光看待现实生活、用数学的思维思考现实生活、用数学的语言表达现实生活、用数学的模型处理现实生活.

引领学生探究：

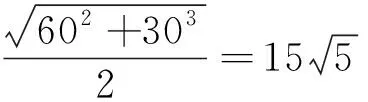
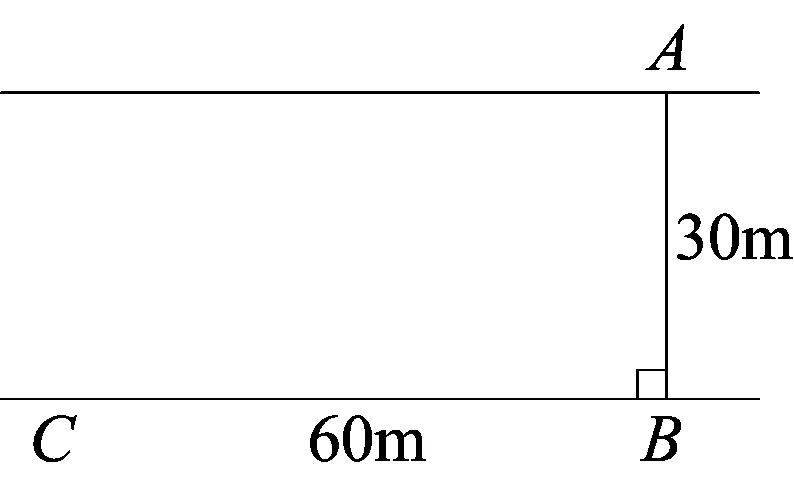
第二层次思考建模，导数求解.从三种特殊情形出发，发现沿折线段CBA救人时间最短，自然联想：还有没有路径用时最短的呢？设先沿线段CB跑步到E,CE=x,再从E游泳到A,需要的时间是y,则

.

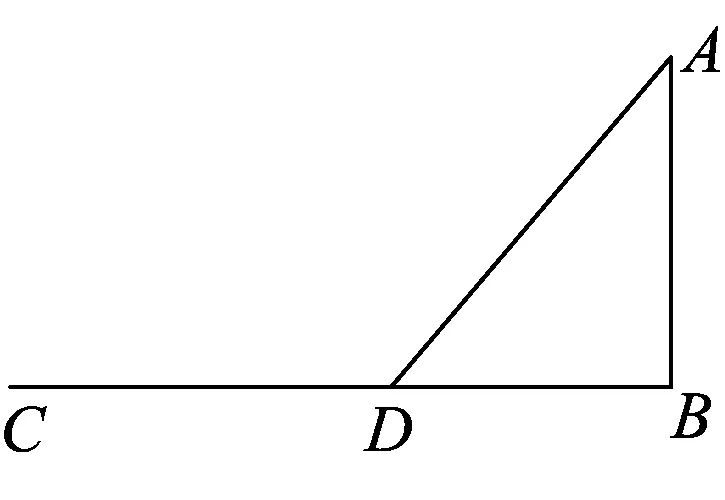
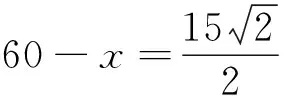
第三层次引申推广，思维升华.一般地，设CA=m,CB==p,AB=n,m、n、p满足m2=n2+p2.从A出发沿直线段CB至D、再从D至A,CD=x,所需要的时间为y,沿直线段CB的速度是v1,沿直线段DA的速度是v2,且v1>v2.

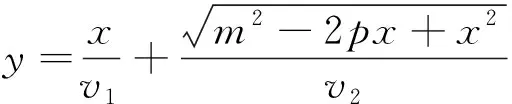
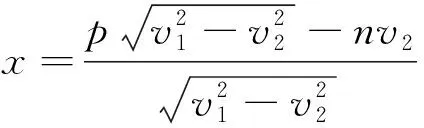
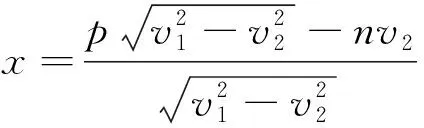
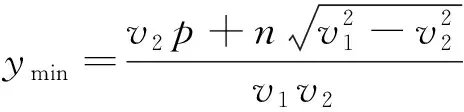
这就是一般性结论.

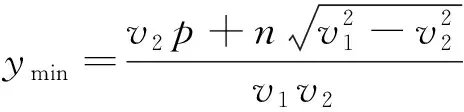
一个有文化色彩的例题, 让学生的思维活动上升到一个更高的层次！

4 课堂小结中的文化色彩

有人说，人类社会的发展经历了三个阶段：一是发现了人，把人从动物世界中解放出来；二是发现了女性，把女性从男性世界中解放出来；三是发现了儿童(学生)，把儿童从成人世界中解放出来.当今社会正处于第三个阶段.发现儿童就是要发现儿童的差异、发现儿童的个性、发现儿童的兴趣、发现儿童的潜能、发现儿童的创造力. 课堂小结是课堂教学的重要环节，它既是对本节课所学知识、方法和思想的高度浓缩、提炼与概括，帮助学生在整体上把握这节课的核心要素，又应该是对后续学习内容的一种预见，给学生留点余地、给学生留点思考和创造的空间.

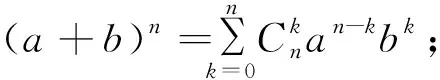
又比如复合函数课这样结尾，复合函数φ(h(g(f(x))))的意义可以这样诠释：设x表示学生，f表示文化课成绩，g表示行为规范，h表示道德品质，φ表示综合素养. 则f(x)表示文化课成绩作用后的学生A，g(f(x))表示行为规范对学生A作用后的学生B，h(g(f(x)))表示道德品质对学生B作用后的学生C，φ(h(g(f(x))))表示综合素养对学生C作用后的学生D，则学生D就是一位全面发展的人，即φ(h(g(f(x))))的结果就是合格的社会公民——基础教育的目标，基础教育的目标还可以用复合函数来表示, 学生兴趣倍增——对数学的文化价值有全新的认识与理解.

一个有文化色彩的结尾，数学思维、数学应用、数学之美尽现其中, 让学生豁然开朗，充分感受数学科学的巨大魅力.

1 中华人民共和国教育部制定.普通高中数学课程标准(2017年版)[M].北京：人民教育出版社，2017

2 曹才翰，章建跃. 数学教育心理学[M]. 北京：北京师范大学出版社，1999

3 李昭平.数学课堂渗透人文教育的实践探索[J].中学数学杂志 (高中版),2011 (5)

4 李昭平.对数学建模的逆向思考——一节“数学问题实际化”教学的有益尝试[J].数学大世界(高中版), 2017 (7)