微流控芯片通道结构的拓扑优化研究

董馨,刘小民

(西安交通大学能源与动力工程学院,710049,西安)

微流控芯片的微流动通道加工技术和结构布置一直为学术界与工业界所重视,它除了连接流体器件的出口和入口、起到连通作用之外,还具有流量分配、试剂混合等功能,同时也希望流体流经微流通道时能够将某些目标值降到最小,如能量耗散、阻力、压降等,以满足微流控芯片能耗低的优点。

文献[1]采用电学比拟法研究了Stokes流动的流道流量分配设计,但电学比拟法只能作为一个近似求解方法,不能准确地设计高精度的流体网络。文献[2]设计了一种用于试剂混合的微通道,由T型微通道和Y型微通道组合而成,其中T型微通道用于制备微液柱,Y型微通道和T型微通道组合用于两种试剂混合。现有的这些微流设备的设计大部分都只是基于设计者的经验和直觉,或者依赖于研究者的尝试改进方法进行的。这些设计方法带有较大的随机性,很难获得具有最佳性能的设计构型。

部分研究者基于数值分析技术的尺寸优化、形状优化和拓扑优化方法对微流器件进行设计和改进。文献[3]首次将拓扑优化设计引入流体力学领域。文献[4-6]对中低雷诺数下的二维定常不可压缩黏性层流流动进行拓扑优化设计,并将Stokes流动扩展到Navier-Stokes流动,以此对文献[3]的工作进行延伸。拓扑优化作为更高层次的优化方法,得到的设计结果更加合理,且不受原有微流通道拓扑结构的限制。文献[7]首次采用密度类拓扑优化方法,通过对不同雷诺数下牛顿流体和非牛顿流体进行拓扑优化,研究对象是Carreau-Yasuda非牛顿本构模型。Jensen等采用变密度方法研究了记忆型非牛顿流体的拓扑优化[8-9]。文献[10]运用变密度方法,研究了剪切渐薄效应的非牛顿流体拓扑优化,以达到壁面应力最小化的目标。文献[11]研究了幂率型非牛顿流体拓扑优化,并比较了剪切渐薄和剪切渐厚非牛顿流体拓扑优化的设计结果。

基于以上分析,本文采用基于真实血液改进的Cross非牛顿流体模型,对双进口-单出口的微流道进行结构拓扑优化设计,分别以能量耗散函数和压降函数为目标,比较分析了非牛顿效应和流道长度对最优拓扑结构的影响。

1 数学描述

1.1 牛顿流体流动的描述

在微流控芯片试样中,大部分流体属于牛顿流体且满足不可压缩条件,特征是应力和应变满足本构方程

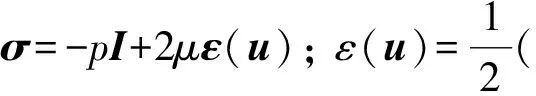
(1)

式中:σ为应力张量;ε为应变张量;u为流体的流动速度;p为流体压强;μ为流体的动力黏度。

设Ω是一个具有Lipschitz连续边界Γ=∂Ω的有界开区域,代表的是流体区域,则二维不可压缩定常流动的Navier-Stokes方程可表示为

(2)

式中:ρ为流体密度;f为流体微元所受体积力。

1.2 非牛顿流体流动的描述

微流控芯片在生物医学行业具有广泛应用,这些应用包括遗传和单细胞分析、蛋白质研究、细胞迁移、药物筛选、干细胞和神经细胞培养等[12-14],其中常涉及血液这一典型的非牛顿流体。非牛顿流体的应力和应变率之间不遵循牛顿内摩擦定律,考虑血液的剪切渐薄效应,本文将动力黏度选择为改进的Cross模型[15]

(3)

式中:μ(γ1)为动力黏度;μ∞和μ0分别代表着无限剪切黏性和零剪切黏性。参数取值[16-17]:μ∞=3.5 mPa·s,μ0=0.16 Pa·s,λ=0.82 s,a=1.23,b=0.64,血液密度ρ=1.058 g/cm3。其中,剪切率γ1表达式如下

(4)

1.3 Navier-Stokes流动拓扑优化问题

文献[3]提出了定常Stokes流动的密度法拓扑优化模型,随后文献[5]提出定常Navier-Stokes流动的密度法拓扑优化模型。该模型是通过在Navier-Stokes方程中加入人工Darcy摩擦力进行的,将式(2)的体力项设为

f=-α(γ)u

(5)

式中:α可以用来表征多孔介质内流动的流体渗透率,它是设计变量(即优化变量)γ的一个插值函数

(6)

式中:αmin和αmax分别为α(γ)的最大值和最小值,αmin一般取为0,αmax取值越大则黏滞力越大,固体渗透率越小(原则上渗透越小越接近真实的情况)。但是,由于拓扑优化中密度法依赖于流体的渗透,在αmax取值太大时容易出现数值不稳定的情况,一般取足够大但有限的值以保证优化问题的数值稳定性且接近真实情况。设计变量γ在0与1之间取值,γ取0对应于固相材质,γ取1对应于液相材质。q为正实数,用来调节插值曲线的凹凸性α(γ),q的取值会影响管道收敛的灰度,一般取值为1。

针对牛顿流体和非牛顿流体的Navier-Stokes流动,建立如下的拓扑优化问题

(7)

计算区域示意图如图1所示,设计域的长、宽分别为L和H,长度单位为mm。在本文中,长度分别选取L=0.5H(短管),L=H(方管),L=2H(长管),以这3种长度为代表进行优化设计,分析微流通道长度对通道结构最优形状的影响。

这里,分别选择压降和能量耗散为优化目标函数,相应的函数表达式如下

J1(Ω)=

(8)

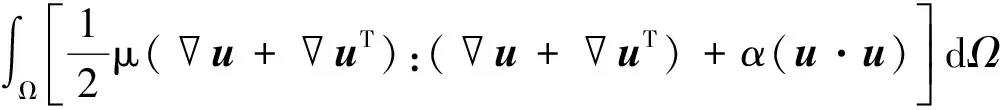
(9)

图1 双进-单出微通道设计区域示意图

2 数值算例

2.1 最小化压力降

选择最小化进出口压力降为优化目标,即以降低微流通道的沿程压力损失、增大流体的流动速度为目标,改善流体在微流体器件中的流动特性。微通道系统的压降接近于系统总压降,可近似为系统总的机械能损失,即流动阻力损失。微通道系统的压降表达如下

(10)

式中:γ2为流体的比重,γ2=ρg,g为重力加速度。高度变化引起的相对压降和速度能可以忽略不计,式(10)简化为

(11)

考虑到微流通道进出口流量的不均匀性,因此目标函数为进出口积分值之差,即以目标函数为压降的表达式见式(8)。

目标函数为压力降函数的非牛顿流体在Re=0.1(Stokes流动)和Re=100(Navier-Stokes流动)时,对应的3种模型(短管、方管、长管)的拓扑优化设计结果见图2和图3。如图2所示,当Re=0.1时,在3个模型中两条通道双管均在设计域的1.5 mm处汇合为单管,随后从出口流出,表明在小雷诺数下(近似为Stokes流动),微管道长度对于非牛顿流体双管的汇合点的位置没有影响。

由表1给出的目标函数值可知,由于压降相同,即系统的流动损失相同,近似为沿程阻力损失相同,表明随着微通道长度增加,双管流动部分的管径必须增加,以保证沿程阻力损失不变。

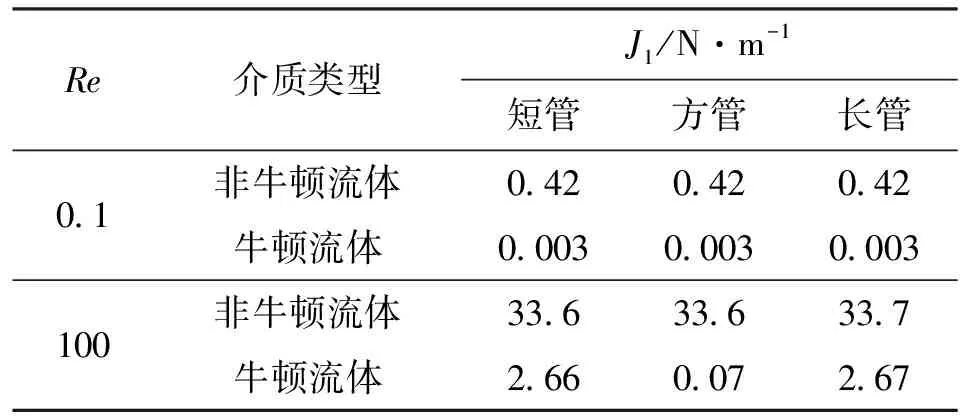
表1 压力降函数的目标函数值

(a)短管 (b)方管

(c)长管图2 Re=0.1时最小化压力降的非牛顿流体微通道最优拓扑结构及速度矢量分布

如图3所示,当Re=100时,设计域中进口处流动的角度随着流道长度增加而减小,在长管中进口角为0°,3个模型中两条通道双管分别在设计域的1.9、3、5.1 mm处汇合为单管。计算结果表明,在较大雷诺数下,双管的汇合点会随着管道的长度增加向后延迟,同时双管流动部分的管径也随之增加。原因是:Stokes流体流动速度较小,黏性力占优,在双管流动中黏性摩擦较大,减少双管流动部分可有效减小压力损耗;而Navier-Stokes流体流速较大,惯性力占优,黏性摩擦的作用较小,惯性力促使双管流动部分增加。

将图2与图3相同模型的最优结构进行对比分析,结果表明雷诺数的增大导致汇合点后移。这是由于随着雷诺数的增大,黏性力与惯性力相比逐渐可以忽略不计,流动速度增大会使流体在双管中流动时间更长,从而延后了汇合点。

图4和图5分别给出了图2和图3对应的动力黏度云图,表明通道中心处流体黏性最大,流动时由流体本身产生的摩擦阻力最大。Re=0.1比Re=100时的流体的黏性梯度变化大,这会导致非牛顿效应在Stokes流动中更加突出;在Navier-Stokes流动的最优拓扑结构中,由于非牛顿流体的黏性梯度变化不明显,使得它与牛顿流体的最优结构相似,此时可以忽略非牛顿流体黏性效应的作用。

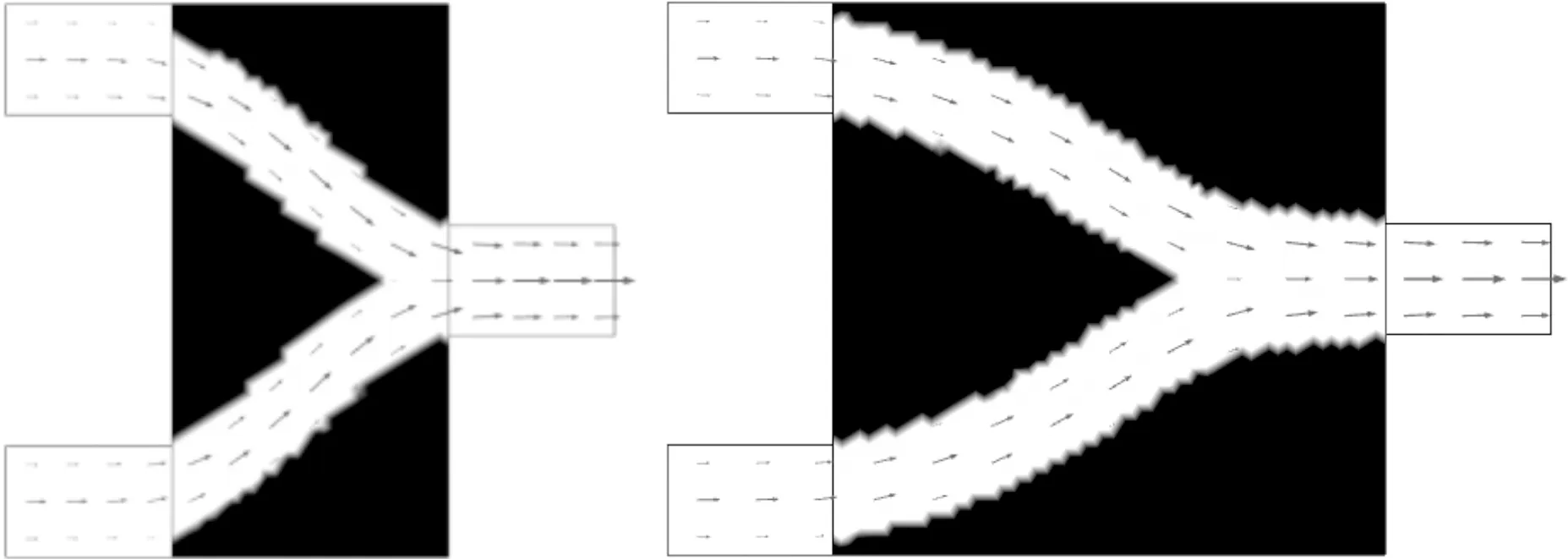
(a)短管 (b)方管

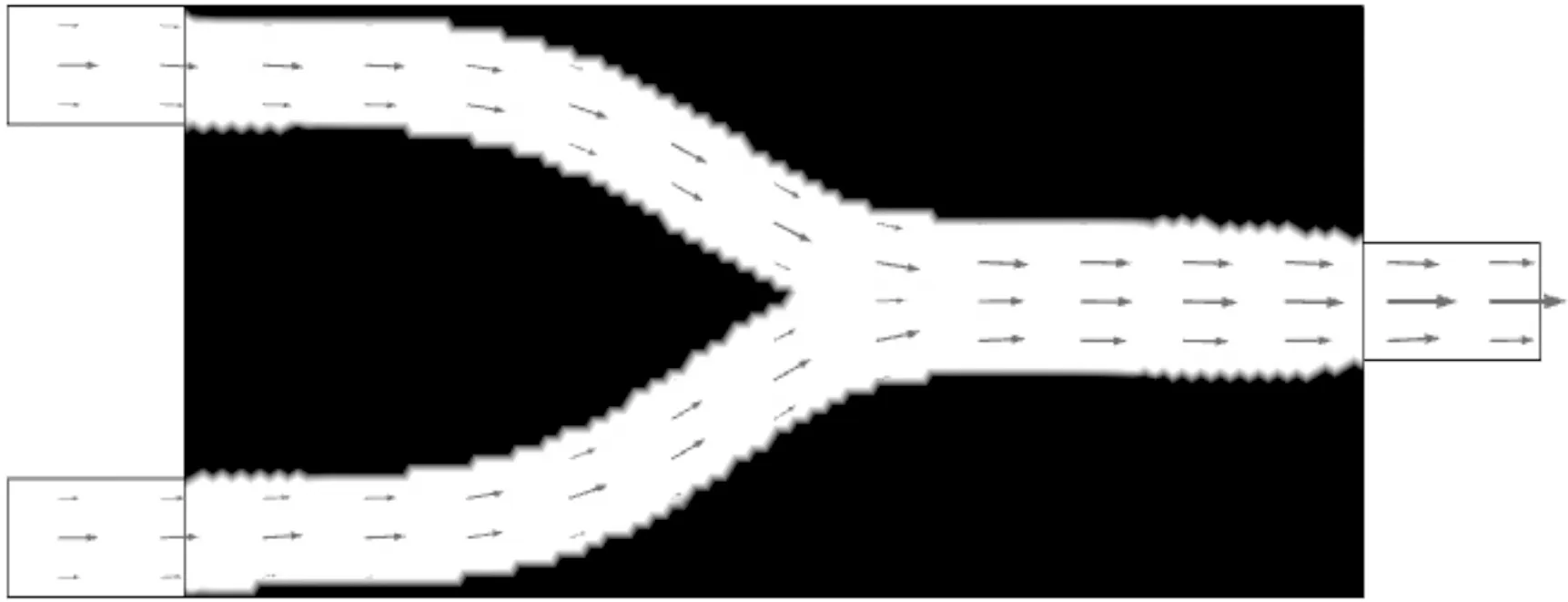
(c)长管图3 Re=100时最小化压力降的非牛顿流体微通道最优拓扑结构及速度矢量分布

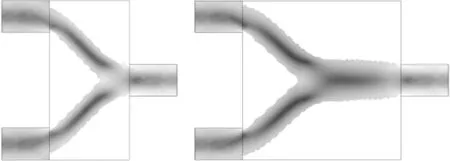
(a)短管 (b)方管

(c)长管图4 Re=0.1时最小化压力降的非牛顿流体黏性分布

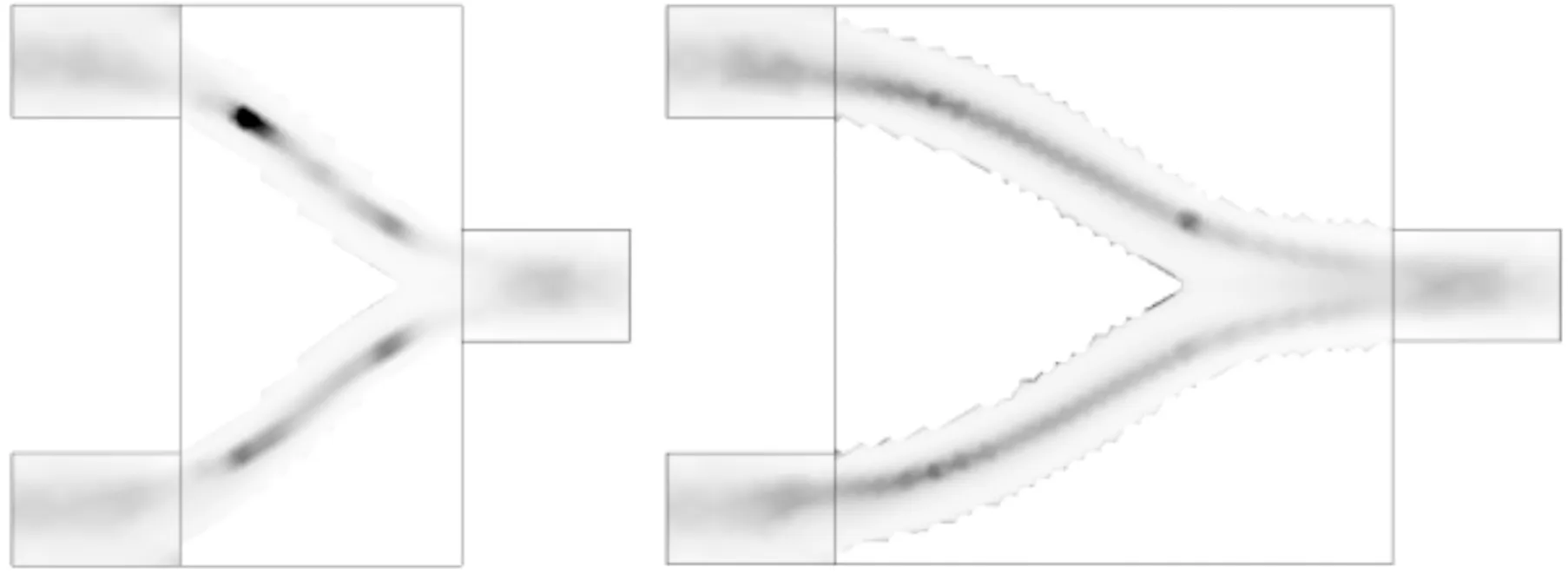
(a)短管 (b)方管

(c)长管图5 Re=100时最小化压力降的非牛顿流体黏性分布

(a)短管 (b)方管

(c)长管图6 Re=0.1时最小化压力降的牛顿流体微通道最优拓扑结构及速度矢量分布

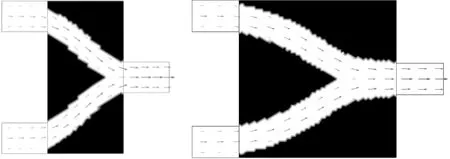
(a)短管 (b)方管

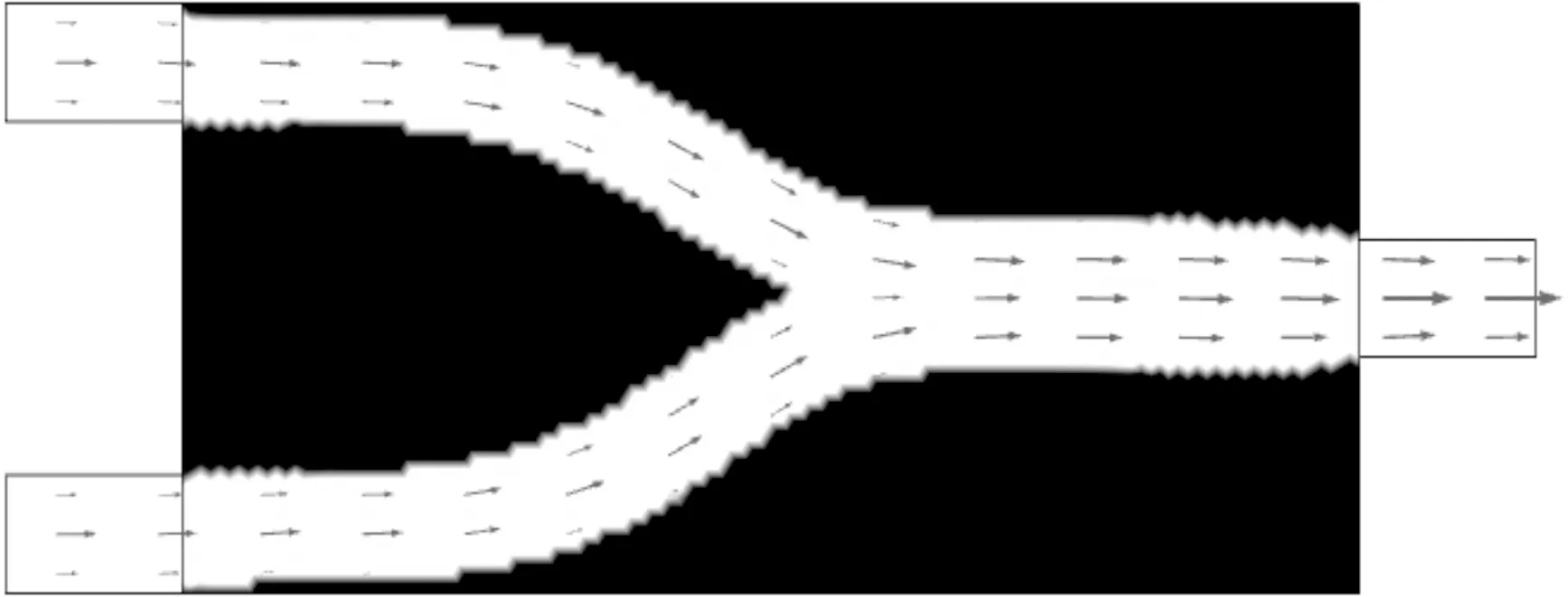
(c)长管图7 Re=100时最小化压力降的牛顿流体微通道最优拓扑结构及速度矢量分布

目标函数为压力降的牛顿流体在Re=0.1(Stokes流动)和Re=100(Navier-Stokes流动)时,对应的3种模型(短管、方管、长管)的拓扑优化设计结果见图6和图7。对比分析可以看到:当Re=0.1和Re=100时,随着模型长度的增加,两条流道汇合点的水平距离都在增加;同一种模型下,不同雷诺数下的最优流道结构也基本相同。由此可得出结论:当流动介质为牛顿流体时,在双-单管通道的结构中,层流小雷诺数下的最优拓扑结构不随雷诺数产生较明显的改变。

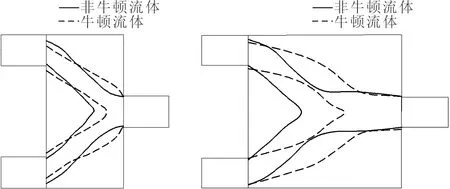
(a)短管 (b)方管

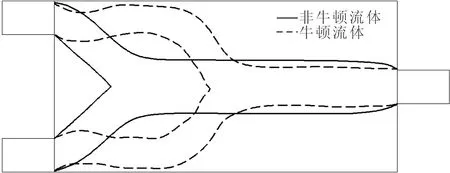
(c)长管图8 Re=0.1时非牛顿流体与牛顿流体微通道最优结构的交叉对比

(a)短管 (b)方管

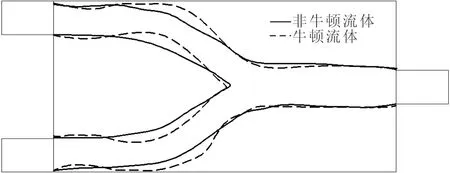
(c)长管图9 Re=100时非牛顿流体与牛顿流体微通道最优结构的交叉对比

图8和图9分别交叉对比了非牛顿流体与牛顿流体在Re=0.1和Re=100时同一工况下的最优结构。当Re=0.1时,非牛顿流体微通道的汇合点都比牛顿流体汇合点靠前,且随着微通道长度的增加,2个汇合点的距离也随之增加;当Re=100时,两条线基本重合,汇合点都随着微通道长度的增加而产生后移。这说明:在以压力降为目标函数的双进-单出管微流通道最优拓扑结构中,非牛顿效应主要体现在黏性力占优的Stokes流动中;对于惯性力不可忽略的Navier-Stokes流动来说,当介质为非牛顿流体时,可将其近似作为牛顿流体处理,以减少计算和设计的工作量。

2.2 最小化能量耗散

微流控芯片的特点之一为低能耗,这就要求流体在流经通道时的能量耗散尽可能小,能量耗散的目标函数表达见式(9)。

由上节的结论可知,非牛顿流体在Stokes流动中的非牛顿效应比Navier-Stokes流动中明显,而且在微流控芯片中,流动速度非常低,相较于较大的黏性力可忽略掉惯性项,近似为Stokes流动。因此,在下面的算例中,只选取Re=0.1为例进行优化设计。

(a)短管 (b)方管

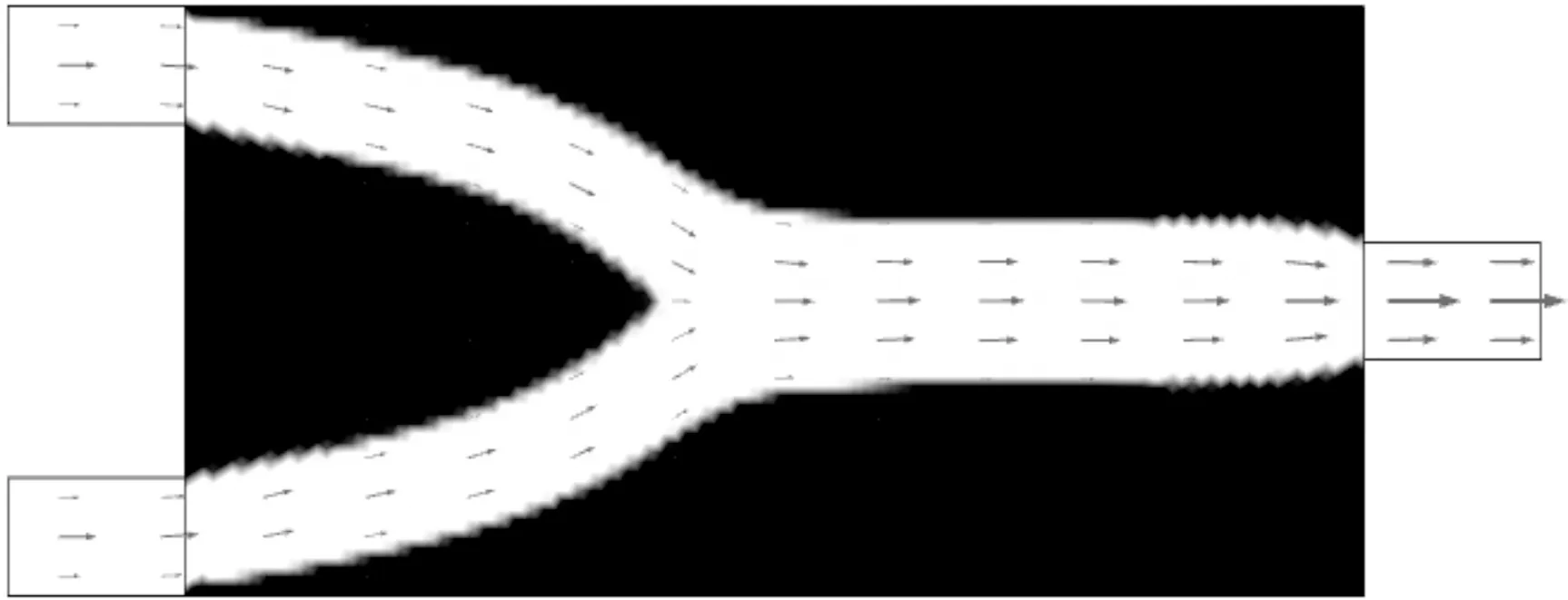
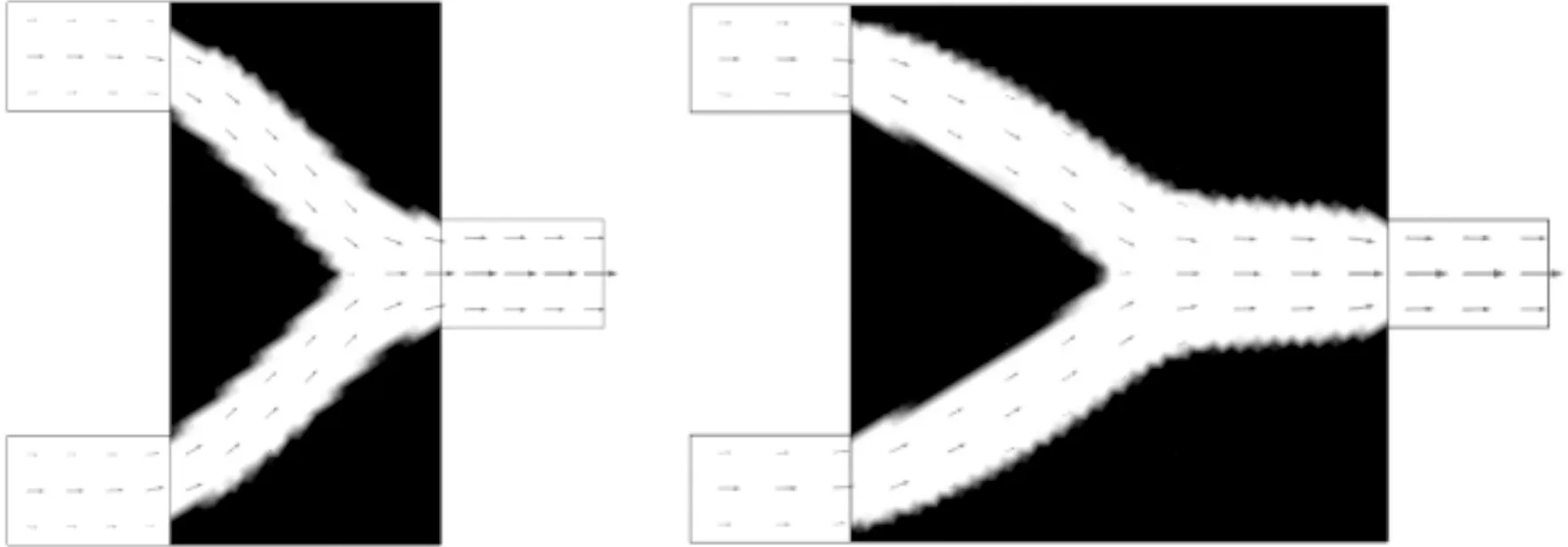
(c)长管图10 最小化能量耗散的非牛顿流体微通道最优拓扑结构及速度矢量分布

(a)短管 (b)方管

目标函数为能量耗散函数的非牛顿流体在Re=0.1(Stokes流动)时,对应的3种模型拓扑优化设计结果见图10,图11为黏性分布云图。由此可知,随着微流通道变长,汇合点不断延后。当优化目标为最小化压力降函数时,要求流体降低沿程损失,以增加流体流动速度,因此两条流道提前汇合可以减小沿程损失,达到压力降最小的目标。当目标函数为能量耗散函数,考虑到两条流道汇合时所产生的黏性耗散和摩擦耗散,模型长度增加使汇合点产生一定的延后,有助于使能量耗散更小。黏性分布图表明,通道中心处的黏性较大,汇合后的黏性比双管流动的黏性有所减小。短管、方管和长管的目标函数值分别为7.4×10-7、8.2×10-7和1.2×10-6W/m,表明通过最优拓扑设计只能使能量耗散增幅减小,但随着长度增加必然会引起能量耗散值的增大。

(c)长管图11 最小化能量耗散的非牛顿流体微通道黏性分布云图

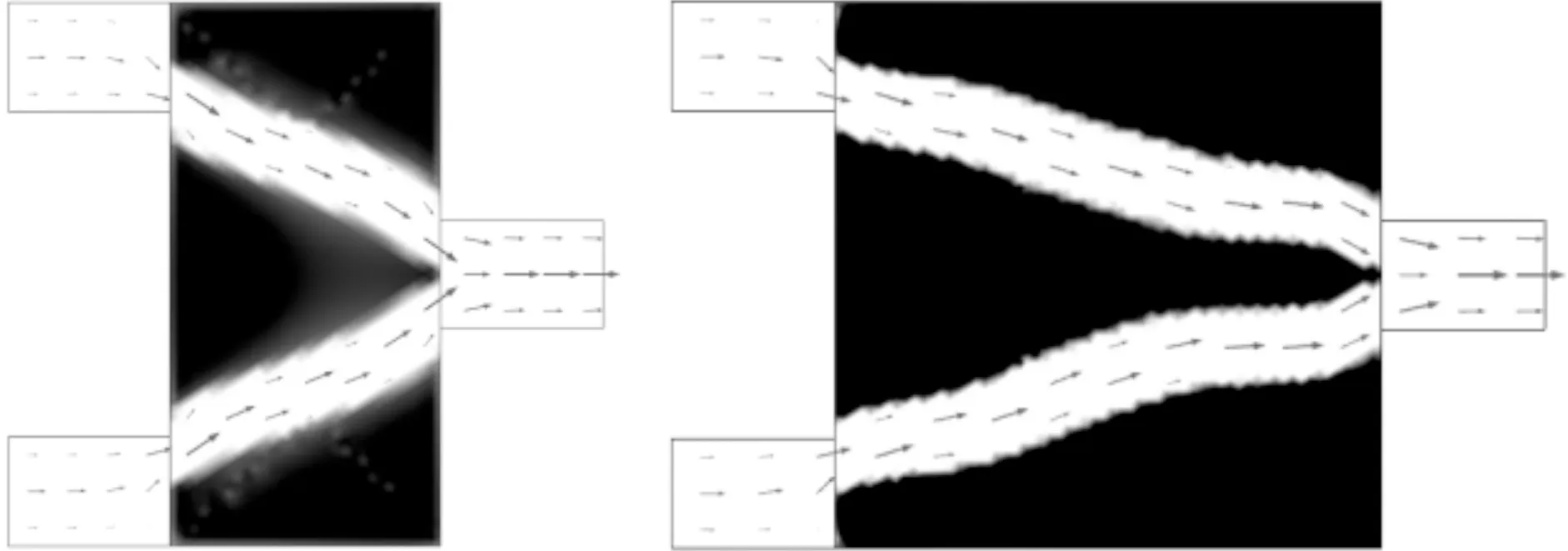
当目标函数为能量耗散函数的牛顿流体在Re=0.1(Stokes流动)时,对应的3种模型拓扑优化设计结果见图12。短管和方管最优结构的双管在设计域中没有汇合,而长管的最优结构是在约1/3处汇合为单管,而后在约2/3处又分流为上下对称的两条流道,最后在设计域的出口处经两条流道流出。长管汇合为单通道后又分流为双通道的原因是为了降低流动速度,从而减小流动中的黏性摩擦力,且双管中总的耗散比继续保持单管流动状态的耗散小,因此最优拓扑结构如图12c所示。目标函数值分别为5.1×10-9、6×10-9和1.4×10-8W/m。

(a)短管 (b)方管

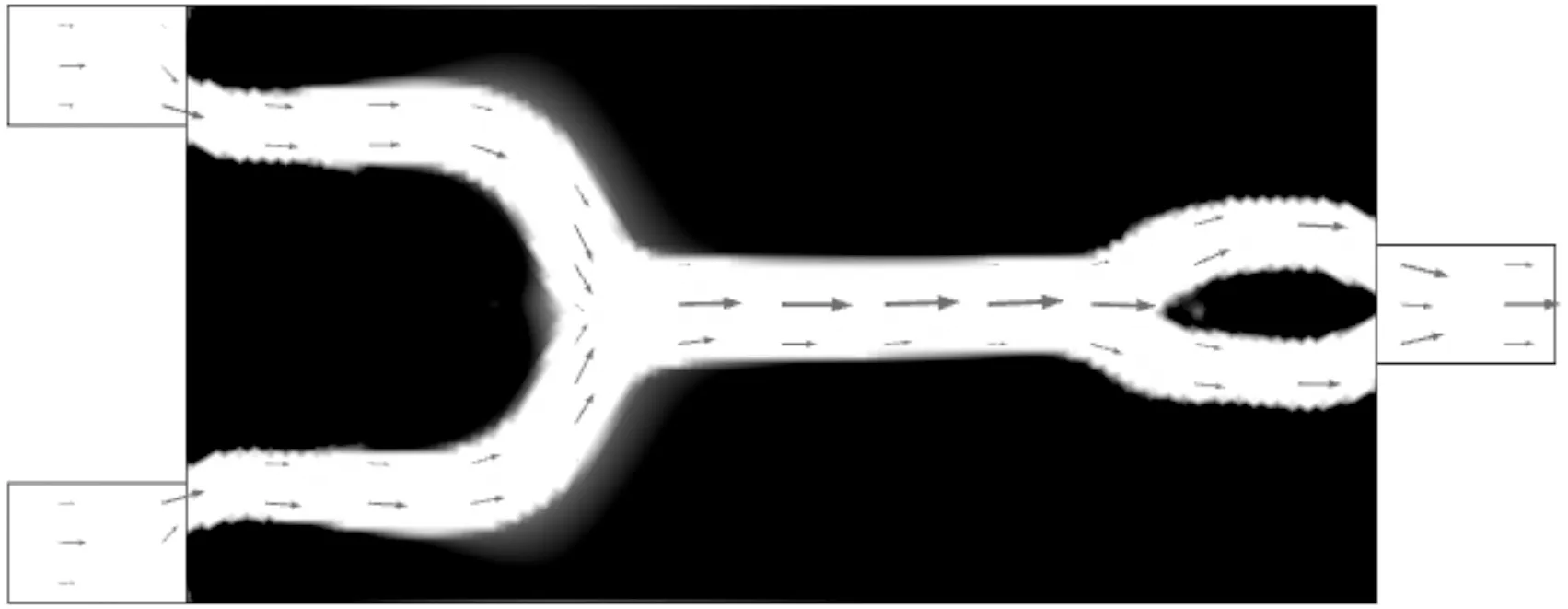
(c)长管图12 最小化能量耗散函数的牛顿流体微通道最优拓扑结构及其速度矢量分布

3 结 论

本文针对两种雷诺数条件下的双进-单出型微流道结构进行拓扑优化研究,获得的主要结论如下。

(1)非牛顿效应对Stokes流体的敏感性较高,在双进-单出通道的最小化压力降最优拓扑结构中,双管的汇合点不随微通道长度改变发生变化;介质为牛顿流体时,随着流道长度增加,汇合点也随之后延。上述差别在Navier-Stokes流动中并没有体现,因此在基于Stokes流动的微流控芯片通道结构设计中,要充分考虑非牛顿效应。

(2)在最小化压力降为目标的牛顿流体微流道拓扑优化设计中,层流小雷诺数(包括Re为0.1和100)下,相同双进-单出微通道模型的最优拓扑结构基本相同,不随雷诺数产生改变。

(3)在非牛顿流体的Stokes流动中,当目标函数为压力降函数时,双进-单出微通道的汇合点不随通道长度的改变产生变化;当目标函数为能量耗散函数时,双进-单出微通道的汇合点随着微通道长度的增加而后延。这表明,微流通道压力降主要体现在双管流动时的沿程损失,汇合变为单管能够有效减小损失,从而降低压力降;而能量耗散与双管结构的角度、长度、汇合点都有关,主要是降低微通道内流体流动时的黏性耗散与汇合时流体间的摩擦耗散。

参考文献:

[1] OH K W,LEE K,AHN B,et al. Design of pressure-driven microfluidic networks using electric circuit analogy [J]. Lab on A Chip,2012,12(3): 515-545.

[2] 王志鑫. 用于混合及微液柱制备的微流控芯片设计与制备 [D]. 北京: 北京化工大学,2014: 1-9.

[3] BORRVALL T,PETERSSON J. Topology optimization of fluids in stokes flow [J]. International Journal for Numerical Methods in Fluids,2010,41(1): 77-107.

[4] EVGRAFOV A. Topology optimization of slightly compressible fluids & dagger [J]. Journal of Applied Mathematics and Mechanics,2010,86(1): 46-62.

[5] GERSBORG-HANSEN A,SIGMUND O,HABER R B. Topology optimization of channel flow problems [J]. Structural & Multidisciplinary Optimization,2005,30(3): 181-192.

[6] LIU Z,GAO Q,ZHANG P,et al. Topology optimization of fluid channels with flow rate equality constraints [J]. Structural & Multidisciplinary Optimization,2011,44(1): 31-37.

[7] PINGEN G,MAUTE K. Optimal design for non-Newtonian flows using a topology optimization approach [J]. Computers & Mathematics with Applications,2010,59(7): 2340-2350.

[8] EJLEBJERG J K,SZABO P,OKKELS F. Topology optimization of viscoelastic rectifiers [J]. Applied Physics Letters,2012,100(23): 234102.

[9] JENSEN K E,SZABO P,OKKELS F. Optimization of bistable viscoelastic systems [J]. Structural & Multidisciplinary Optimization,2014,49(5): 733-742.

[10] HYUN J,WANG S,YANG S. Topology optimization of the shear thinning non-Newtonian fluidic systems for minimizing wall shear stress [J]. Computers & Mathematics with Applications,2014,67(5): 1154-1170.

[11] ZHANG B,LIU X M,SUN J J. Topology optimization design of non-Newtonian roller-type viscous micropumps [J]. Structural & Multidisciplinary Optimization,2016,53(3): 409-424.

[12] BLAZEJ R G,KUMARESAN P,MATHIES R A. Microfabricated bioprocessor for integrated nanoliter-scale Sanger DNA sequencing [J]. Proceedings of the National Academy of Sciences of the United States of America,2006,103(19): 7240-7245.

[13] GAO J,YIN X F,FANG Z L. Integration of single cell injection,cell lysis,separation and detection of intracellular constituents on a microfluidic chip [J]. Lab on A Chip,2004,4(1): 47-52.

[14] LAGALLY E T,SCHERER J R,BLAZEJ R G,et al. Integrated portable genetic analysis microsystem for pathogen/infectious disease detection [J]. Analytical Chemistry,2004,76(11): 3162-3170.

[15] ZHANG B,LIU X. Topology optimization study of arterial bypass configurations using the level set method [J]. Structural & Multidisciplinary Optimization,2014,51(3): 1-26.

[16] ABRAHAM F,HEINKENSCHLOSS M B. Shape optimization in unsteady blood flow: a numerical study of non-Newtonian effects [J]. Computer Methods in Biomechanics & Biomedical Engineering,2005,8(2): 127-137.

[17] CHEN H,SU J,LI K,et al. A characteristic projection method for incompressible thermal flow [J]. Numerical Heat Transfer: Part B Fundamentals,2014,65(6): 554-590.