证据距离的选取对冲突证据组合影响的研究

周永庆,韩德强,杨艺

(1.西安交通大学电子与信息工程学院,710049,西安; 2.西安交通大学机械结构强度与振动国家重点实验室,710049,西安; 3.西安交通大学航天航空学院,710049,西安)

在Dempster-Shafer(DS)证据理论[1]中,独立证据可以依据证据组合规则进行证据组合。当证据之间存在冲突时,证据组合后的结果往往与实际直觉相悖[2],针对这一情况,出现了许多改进的证据组合规则[3-8],其中有一类是基于证据间距离的冲突证据组合规则[3-5],这类算法用证据之间的距离度量证据之间的相似性,依据相似性得到证据的权值,对证据进行加权融合。在此类方法中,证据距离度量方式对证据组合有重要的影响。

随着证据理论的研究深入,涌现了诸多证据之间距离的度量定义[9],如Jousselme距离[10]、基于Pignistic概率的距离[11]、基于模糊隶属度的距离[12]和基于信任区间的距离[13]等。在既有的基于证据间距离的冲突证据组合研究中,上述距离定义方式均有所采用。邓勇等人依据证据间的Jousselme距离得到证据可靠度,用证据可靠度对证据进行加权融合获取平均证据,再将平均证据进行组合[3]。肖建于等人则基于Pignistic概率距离得到证据的权重,求得平均证据后再进行组合[4]。刘志成等人则依据修正的City Block距离获取证据的权重[5]。在这些方法中,只选取了某一种证据间的距离度量方式,没有对不同的证据距离度量方式进行对比。

为了探究不同的证据距离度量方式对冲突证据组合的影响,从而选取适合加权证据组合权重生成的距离定义,本文将各种距离度量方式应用于基于证据距离修正证据组合的方法中,对比了在不同的距离度量方式下,证据可靠度的大小和将平均证据组合后所得组合结果之间的差异,分析了产生差异的原因。采用4个算例的实验结果表明,在证据组合过程中,与其他的证据距离相比,采用本文方法选取的证据距离所求得的证据可靠度更符合实际,体现证据差异更有效。

1 证据理论概述

设Θ为辨识框架,若集函数m:2Θ→[0,1]满足

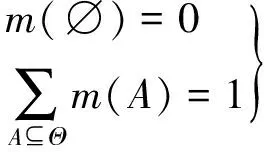
(1)

则称m为Θ上的Mass函数。Mass函数实际上就是对各种假设的评价权值。其中,使得m(A)>0的A称为焦元。

在辨识框架Θ上的某个命题A的信任函数(belief function)定义为

(2)

似真度函数(plausibility function)定义为

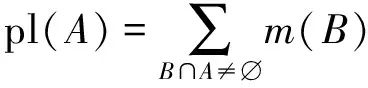
(3)

区间[bel(A),pl(A)]为信任区间,用以表示对命题(焦元)A的不确定程度。

Dempster组合规则也称证据组合公式,其定义为:设统一辨识框架上的两个独立证据,其相应的mass函数分别为m1和m2,∀A⊆Θ,A≠∅,则组合之后证据为

(4)

在将证据进行融合之后,需要将融合结果的mass函数转化为概率以便于进行决策。Mass函数转化为概率有多种方法,一种经典的方法为Smets提出的Pignistic概率转换方法[14]

(5)

2 冲突证据组合方法

2.1 证据冲突现象

当证据之间存在较大冲突的时候,应用Dempster组合规则融合后得到的结果往往与直观结果相违背。以下为Zadeh所举的经典算例[2]。

两名医生为同一个病人看病,该病人可能得的病为脑膜炎(M)、脑震荡(C)和脑肿瘤(T),即辨识框架为Θ={M,C,T}。两名医生给出的各种病症的可能结果如下

m1({M})=0.99;m1({T})=0.01

m2({C})=0.99;m2({T})=0.01

将以上两个独立证据应用Dempster组合规则进行融合,得到融合后的结果为m({T})=1,此时的冲突系数K=0.999 9。

在这个例子中,两名医生均认为该病人所得的病是脑肿瘤(T)这件事的可能性很低,但是应用Dempster组合规则融合后的结果却表明该病人得的病只可能是脑肿瘤(T),这与两名医生的判断均相悖,不符合直观结果。这个例子表明,在证据存在较高冲突的情况下,应用Dempster组合规则得到的结果会反直观。此外,Dempster组合规则并不满足幂等性,即使证据体都相同,组合过程中也会产生信任偏移[15],在某些情况下还会出现证据吸收的问题[16]。

针对证据冲突问题,一种观点归因于融合规则本身的缺陷,对融合规则进行了修正,如在Yager提出的规则[6]中,将冲突赋给全集;Dubois等则将焦元的并集引入到证据组合规则中[7]。另一种观点认为该问题是由证据本身的不准确、不可靠所造成的,因此应该对证据进行进一步修正,如Murphy采用求平均的方式来对证据进行修正[8],邓勇、肖建于、刘志成等人则基于证据距离来构造证据权值,对证据进行加权融合[3-5]等。

2.2 基于证据距离的证据修正与组合方法

在基于证据距离的证据修正与组合方法中,邓勇等人所提出的方法具有代表性。在该方法中,核心概念为证据可靠度,它描述了证据的可靠程度。用证据可靠度作为权值来对证据进行加权,得到融合后的证据。关于证据可靠性的评估,学者们做了许多的研究。Elouedi等人依据可传递信任模型,基于加权后的平均证据应与数据真值距离最小,利用优化方法得到证据可靠度[17]。邢清华等人把各个焦元信任区间的长度之和作为目标函数,通过极小化目标函数得到证据可靠度[18]。付耀文等人借鉴冲突处理中的Dubois & Prade规则,将由冲突得到的折扣量按局部冲突的大小分配给涉及各局部冲突的集合的并,得到证据可靠度[19]。

在邓勇等人的方法中,证据可靠度是基于证据距离构建的,其构建过程如下[3]

sim(mi,mj)=1-d(mi,mj)

(6)

(7)

(8)

式中:cred(mi)为证据mi的可靠度;d(mi,mj)表示证据mi与mj间的证据距离。

得到各个证据的可靠度之后,就可以用证据可靠度作为权值对证据进行加权融合,得到平均证据。

假设有s个证据,则平均证据为

(9)

然后,应用Dempster组合规则对平均证据mave自身组合s-1次。

在该方法中,证据可靠度的求取与证据距离紧密相关。随着证据理论的研究深入,出现了一系列的证据距离定义。不同的距离应用于证据修正,效果或有不同。本文将针对证据距离的不同,对于证据修正与组合效果的影响开展分析研究。在下一节中,将首先介绍几类常用的证据距离,并将不同的证据距离应用于冲突证据组合的方法中进行比较。

3 基于不同证据距离的加权证据融合

3.1 证据距离度量方式

证据距离用来描述证据之间的差异性或者相似性,两组证据之间的距离越大,表明它们之间的差异性越大,相似性越低。几类常用的证据距离度量方式有Jousselme距离[10]、Tessem距离[11]、基于隶属度函数的距离[12]和基于信任区间的距离[13]。

3.1.1 Jousselme距离 Jousselme距离[10]的求取过程如下

(10)

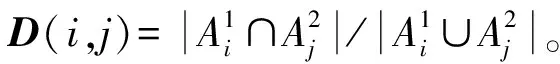
3.1.2 Tessem距离 在Tessem的研究中[11],证据距离的度量是基于pignistic概率的。Mass函数转化为Pignistic概率的公式如下

(11)

Tessem距离定义如下

(12)

3.1.3 基于隶属度函数的距离[12]在模糊理论中,隶属度函数描述了元素属于某一模糊集合的程度。若μA:Θ→[0,1],θ→μA(θ)是在辨识框架Θ上的给定映射,则A是Θ上的模糊集合,μA(θ)是模糊集合A的隶属度函数,μA(θ)在没有混淆时简记为μ(θ)。μ(θi)为单点焦元θi的隶属度函数,μ(θi)可以取θi的信任函数或者似真度函数μ(θi)=bel(θi),或μ(θi)=pl(θi),则基于隶属度函数的证据距离定义为

(13)

式中:符号∧为取小运算(合取);符号∨为取大运算(析取)。

在一个有限的辨识框架中,若单点焦元的隶属度函数之和小于1,则隶属度函数等价于相应焦元的信任函数,若隶属度函数之和大于1,则隶属度函数等价于相应焦元的似真度函数[20]。就实际操作而言,在证据函数中,如果混合焦元多,单点焦元少,此时若使用单点焦元的信任函数作为隶属度函数,会出现较多的0元素,求取距离时实用性较差,因此更倾向于使用似真度函数作为单点焦元的隶属度函数。本文的实验中选取μ(θi)=pl(θi)。

3.1.4 基于信任区间的距离 本课题组以往的工作中设计了一种基于信任区间的距离[13]。若一个焦元在两个证据中的信任区间([bel(A),pl(A)])分别为[a1,b1]和[a2,b2],则基于信任区间的距离定义为

(14)

基于所有信任区间的两个mass函数之间的距离为

(15)

式中:Ai为焦元;B1(Ai)和B2(Ai)分别表示m1和m2中焦元Ai的信任区间;Nc=1/2n-1是归一化因子。

3.2 算例

为了研究证据距离度量方式对证据可靠度以及证据组合结果的影响,设计如下算例。

算例1设辨识框架为Θ={A,B,C},利用6个不同信息源得到的证据函数如下。

m1:m1(A)=0.65,m1(B)=0.2,m1(C)=0.15;

m2:m2(A)=0.55,m2(B)=0.25,m2(C)=0.2;

m3:m3(A)=0.5,m3(B)=0.3,m3(C)=0.2;

m4:m4(A)=0.3,m4(B)=0.35,m4(C)=0.35;

m5:m5(A)=0.1,m5(B)=0.3,m5(C)=0.6;

m6:m6(B)=0.8,m6(C)=0.2。

直观来看,6组证据中第1、2、3组证据相似,其中m(A)最高,第4组证据中m(A)、m(B)、m(C)大小接近,第5组证据中m(C)最高,第6组证据中m(B)最高。

使用邓勇的方法,在不同的证据距离度量方式下求得的各证据可靠度如表1所示。

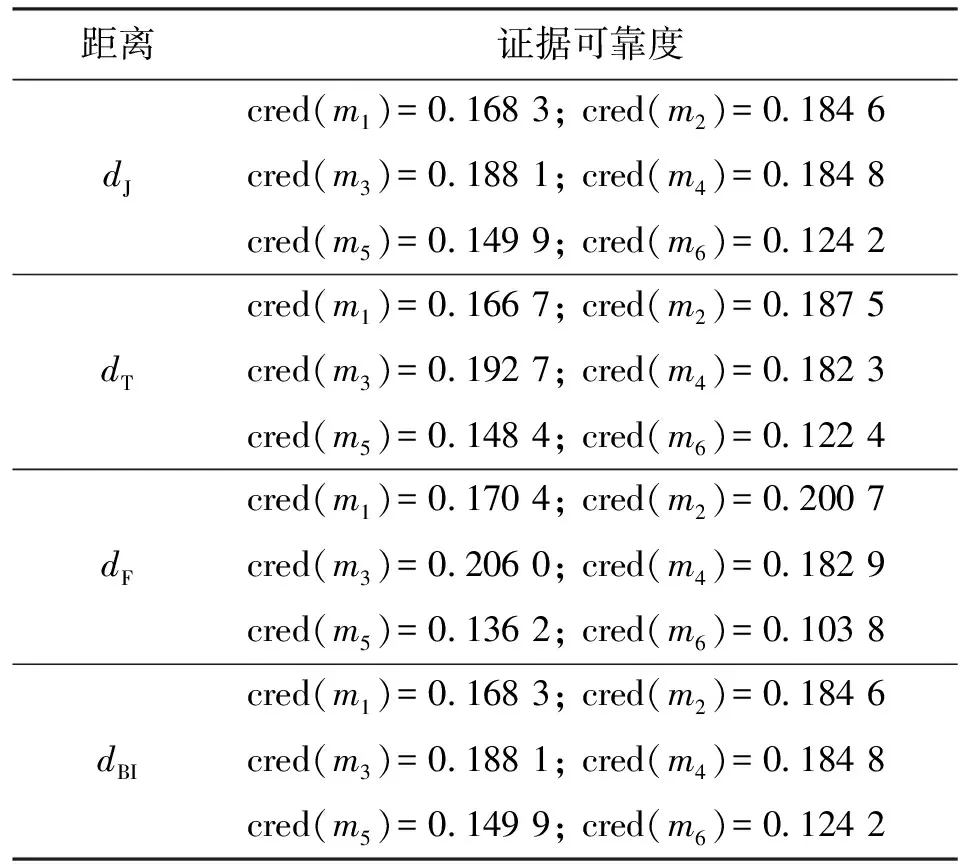
表1 算例1中不同证据距离度量方式下证据可靠度对比

得到证据可靠度后,运用证据可靠度进行加权得到平均证据如表2所示。

表2 算例1中不同证据距离度量方式下的平均证据

应用Dempster组合规则对平均证据自身组合5次,得到融合后的mass函数如表3所示。

表3 算例1中不同证据距离度量方式下组合结果对比

表1中证据可靠度对比结果显示,根据4种证据距离度量方式得到的前4组证据的可靠度均比后两组证据的可靠度高,且最后一组证据的可靠度最小。由于证据可靠度是依据证据之间的相似度得到的,假设多数人给出的信息是可靠的,那么某一条证据与其他证据之间的相似度越高,该条证据的可靠度越大。综合6组证据来看,前3组证据之间的相似度大,它们之间相互支持,因此得到的前3组证据的可靠度高,第4组证据中m(A)、m(B)、m(C)大小接近,后两组证据与前4组证据以及它们中的另一组证据的差异性都很大,所以后两组证据的可靠度较低。表1给出的结果与直观结论相符。

在只有单点焦元有值的情况下,焦元的BetP与mass函数值相等。表3中组合结果对比显示,所有度量方式下组合结果中P(A)都是最大,原因在于前3组证据中的m(A)均为最高,它们之间相互支持,得到的证据可靠度高,加权后平均证据中的m(A)也是最大。在此算例中4种距离度量方式下的证据组合结果在决策方面并无差异。

算例2设辨识框架为Θ={A,B,C},利用6个不同信息源得到的证据函数如下。

m1:m1(A)=0.4,m1(B)=0.3,m1(A∪C)=0.3;

m2:m2(A)=0.5,m2(B)=0.2,m2(A∪B∪C)=0.3;

m3:m3(A)=0.7,m3(B)=0.2,m3(A∪B)=0.1;

m4:m4(A)=0.6,m4(B)=0.3,m4(B∪C)=0.1;

m5:m5(A)=0.2,m5(B)=0.7,m5(A∪C)=0.1;

m6:m6(B)=0.7,m6(C)=0.1,m6(A∪B)=0.2。

与算例1不同的是,算例2中加入了混合焦元,这6组证据中前4组证据相似,其中m(A)大于m(B),后两组证据中m(B)最大。在不同的证据距离度量方式下求得各证据的可靠度,如表4所示。

表4中证据可靠度对比结果显示:在所有的证据距离度量方式下,前4组证据的可靠度均大于后两组证据的可靠度;前4组证据彼此之间的相似度高,支持度大,在假设多数人意见可靠的前提下得到的证据可靠度高,这与直观结果相符合;后两组证据与前4组证据之间的差异较大,可靠度较低。表4给出的结果与直观结论相符。

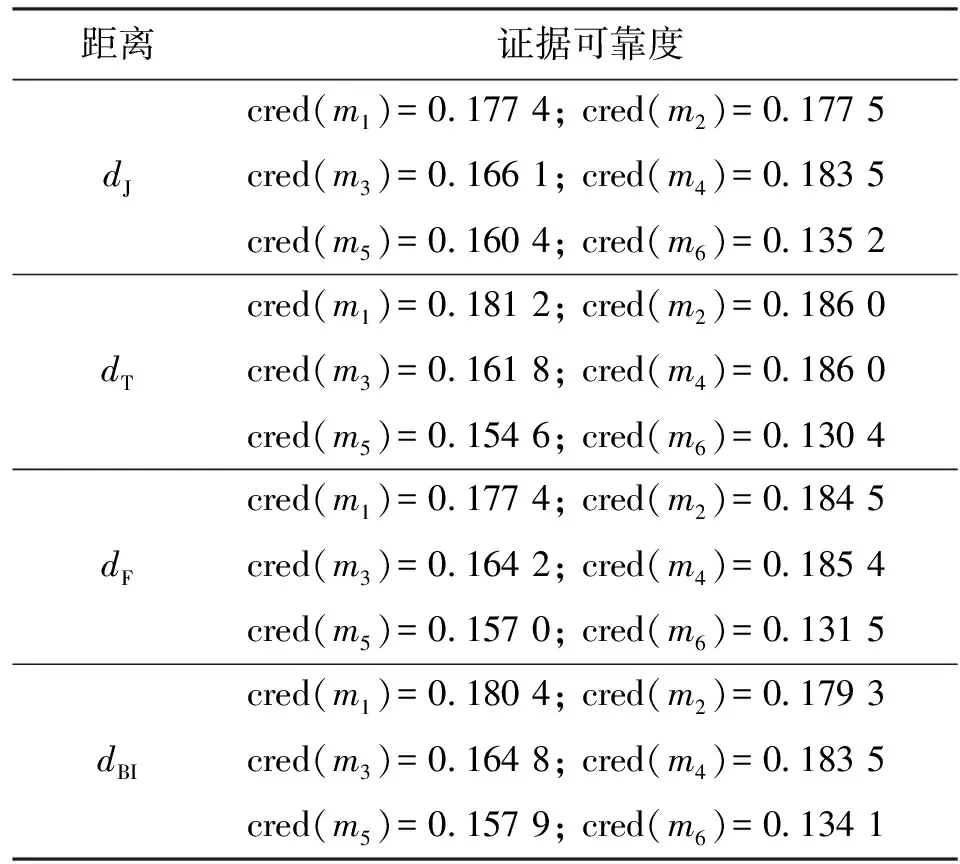
表4 算例2中不同证据距离度量方式下证据可靠度对比

运用证据可靠度对证据进行加权,得到平均证据,如表5所示。

表6组合结果中,m(A∪C)很小,可以认为A、B、C的BetP与A、B、C的mass函数值相等。4种距离度量方式下给出的组合结果相似,其中P(A)大于P(B),P(C)最小。原因在于前4组证据中m(A)最大,它们相互支持,证据可靠度高,在加权的过程中对平均证据的贡献较大,因此平均证据中的m(A)也是最大,如表5所示。表6中的组合结果表明,在证据中存在混合焦元的情况下,4种距离度量方式下的证据组合结果在决策方面也没有差异。

表6 算例2中不同证据距离度量方式下组合结果对比

3.2.3 有关证据距离的分析与探讨 严谨的证据距离应满足以下4条性质[13]:

(1)非负性,d(x,y)≥0;

(2)非退化性,d(x,y)=0⟺x=y;

(3)对称性,d(x,y)=d(y,x);

(4)三角不等式,d(x,y)+d(y,z)≥d(x,z)。

在3.1节提及的4种证据距离中,dJ、dBI是严谨的证据距离[10,13],满足全部4条性质。dF、dT不是严谨的证据距离。算例1和算例2中4种证据距离度量方式下证据可靠度以及证据组合结果均直观、合理,但是在这4种证据距离中,dF、dT这两种距离在计算的过程中进行了框架的切换。其中,dT将证据函数转化到概率框架下计算,dF则将证据函数转化到模糊理论的框架下计算,在框架切换的过程中产生了信息损失[13],由此造成了dF、dT的不严谨性。为了进一步分析证据距离对证据可靠度的影响,举出下面两个算例。

算例3设辨识框架为Θ={A,B,C},利用6个不同信息源得到的证据函数如下。

m1:m1(A)=0.45,m1(B)=0.35,m1(C)=0.05,m1(A∪B)=0.1,m1(A∪B∪C)=0.05;

m2:m2(A)=0.4,m2(B)=0.3,m2(C)=0.1,m2(A∪B)=0.2;

m3:m3(A)=0.5,m3(B)=0.4,m3(A∪B∪C)=0.1;

m4:m4(A)=0.48,m4(B)=0.38,m4(C)=0.02,m4(A∪B)=0.04,m4(A∪B∪C)=0.08;

m5:m5(A)=0.5,m5(B)=0.5;

m6:m6(B)=0.8,m6(C)=0.2。

在这6组证据中,前4组证据相似,其中m(A)略大于m(B),m(C)最小。第5组证据中m(A)与m(B)相同,与前4组证据有一定的相似度。第6组证据中m(B)远大于m(C),与前5组证据的差异较大。在不同证据距离度量方式下得各证据的可靠度，如表7所示。

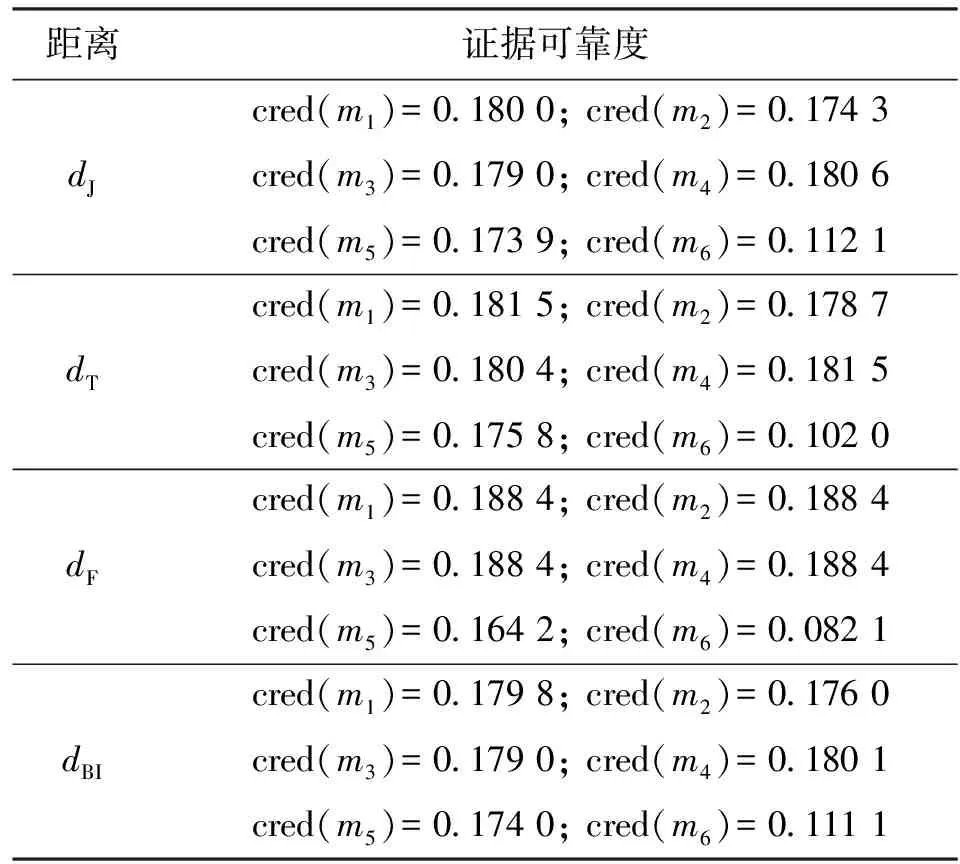
表7 算例3中不同证据距离度量方式下证据可靠度对比

从表7中的证据可靠度对比结果来看,4种证据距离度量方式下得到的前5组证据的可靠度都比较高,最后一组证据的可靠度很低。在假设多数人的信息可靠的前提下与直观结果相吻合。

在dF度量方式下,前4组证据的可靠度相同,且与后两组证据的可靠度相差较大,但是前4组证据并不相同。事实上基于隶属度函数的距离与证据之间的差异并不是一一对应的,如果证据中单点焦元的信任函数或者似真度函数相同,那么在dF度量方式下他们之间的距离为零,即dF不满足非退化性。本例中前4组证据单点焦元的似真度函数相同,即

pl(A)=0.6; pl(B)=0.5; pl(C)=0.1

则依据式(13),m1、m2之间的距离为

类似地,求得这4条证据中任意两条证据之间的距离为零,从而得到这4组证据的可靠度相同。这表明dF度量方式并不能体现出某些证据之间的差异。由此得到的可靠度必然存在偏差。可见证据距离的不严谨会对证据可靠度产生影响。

算例4设辨识框架为Θ={A,B,C},利用6个不同信息源得到的证据函数如下。

m1:m1(A)=0.4,m1(B)=0.4,m1(C)=0.2;

m2:m2(A∪B)=0.8,m2(C)=0.2;

m3:m3(A)=0.4,m3(B)=0.2,m3(B∪C)=0.4;

m4:m4(A)=0.2,m4(C)=0.2,m4(A∪B∪C)=0.6;

m5:m5(C)=0.65,m5(A∪B∪C)=0.35;

m6:m6(A)=0.35,m6(C)=0.65。

在这6组证据中:第1组证据的m(A)、m(B)相同,且大于m(C),第3组证据中m(A)大于m(B);第2组证据中m(C)很小,m(A∪B)较大;第4组证据中m(A)、m(C)相同,均很小,第5组证据中m(C)较大,第6组证据中m(A)小于m(C);第1、第3、第4组证据较为相似。在不同的证据距离度量方式下求得各证据的可靠度，如表8所示。

表8 算例4中不同证据距离度量方式下证据可靠度对比

从表8中的证据可靠度对比结果来看,在dJ、dF、dBI度量方式下得到的第1、3、4组的证据可靠度较大,剩余3组的证据可靠度较小。

在dT度量方式下得到的前3组证据的可靠度相同,但是前3组证据并不相同。事实上,Tessem距离是根据pignistic概率求得的,如果证据的pignistic概率相同,那么在Tessem距离的度量方式下,证据之间的差异就是零。即dT不满足非退化性。本例的前3条证据中,各条证据之间单点焦元的pignistic概率都相同,即

P(A)=0.4;P(B)=0.4;P(C)=0.2

则依据式(12),m1、m2之间的距离为

dT(m1,m2)=max{|0.4-0.4|,|0.4-0.4|,|0.2-0.2|}=0

类似地,求得这3条证据中任意两条证据之间的距离为零,且其他证据到这3条证据的距离都相等,从而得到这3组证据的可靠度相同。这表明,dT度量方式下距离与证据之间的差异也不是一一对应的。可见,证据距离的不严谨会对证据可靠度产生影响。

证据可靠度以及证据组合的合理性受到诸多因素影响,如果基于证据距离构造可靠度并用于证据组合,距离的选取只是其中的一个因素,使用严谨的证据距离并不能够保证得到的证据可靠度和证据组合结果最优。本文关注证据距离对证据可靠度和证据组合的影响,算例表明严谨的证据距离能够更好地表征证据之间的差异,在基于证据距离生成证据可靠度时结果更符合直观。

4 结 论

本文提出一种将不同的证据距离度量方式应用在加权证据组合中的对比方法,对不同证据距离下的加权证据组合过程进行分析比较。实验结果表明,不同的证据距离度量方式对证据可靠度的求取有影响,其中使用dF、dT度量方式在算例中得到的证据可靠度不能体现出证据之间的差异,这与dF、dT的不严谨性有关。本文建议选择dJ、dBI这两种严谨的证据距离。

对于证据冲突问题,本文的解决方式是修改证据体。在未来的工作中,我们将更加关注有关修改证据规则的研究,关注当存在证据冲突时,各类证据距离度量方式对修改后的证据规则的影响。

参考文献:

[1] SHAFER G. A mathematical theory of evidence [M]. Princeton,NJ,USA: Princeton University Press,1976: 1-10.

[2] ZADEH L A. Review of Shafer’s a mathematical theory of evidence [J]. AI Magazine,1984,5(3): 81-83.

[3] DENG Yong,SHI Wenkang,ZHU Zhenfu,et al. Combining belief functions based on distance of evidence [J]. Decision Support Systems,2004,38(3): 489-493.

[4] 肖建于,童敏明,朱昌杰,等. 基于pignistic概率距离的改进证据组合规则 [J]. 上海交通大学学报,2012,46(4): 636-641.

XIAO Jianyu,TONG Minming,ZHU Changjie,et al. Improved combination rule of evidence based on pignistic probability distance [J]. Journal of Shanghai Jiaotong University,2012,46(4): 636-641.

[5] 刘志成,乔慧,何佳洲. 基于加权证据距离的高度冲突证据组合方法 [J]. 计算机工程与应用,2014,50(3): 103-107.

LIU Zhicheng,QIAO Hui,HE Jiazhou. Combination approach of highly conflicting evidence based on weighted distance of evidence [J]. Computer Engineering & Applications,2014,50(3): 103-107.

[6] YAGER R R. On the Dempster-Shafer framework and new combination rules [J]. Information Science,1987,41(2): 93-137.

[7] DUBOIS D,PRADE H. Representation and combination of uncertainty with belief functions and possibility measures [J]. Computational Intelligence,1988(4): 244-264.

[8] MURPHY C K. Combining belief functions when evidence conflicts [J]. Decision Support Systems,2000,29(1): 1-9.

[9] JOUSSELME A L,PATRICK M. Distance in evidence theory: comprehensive survey and generalization [J]. International Journal of Approximate Reasoning,2012,53(2): 118-145.

[10] JOUSSELME A L,GRENIER D,BOSSÉ E. A new distance between two bodies of evidence [J]. Information Fusion,2001,2(2): 91-101.

[11] TESSEM B. Approximations for efficient computation in the theory of evidence [J]. Artificial Intelligence,1993,61(2): 315-329.

[12] HAN Deqiang,DEZERT J,HAN Chongzhao,et al. New dissimilarity measures in evidence theory [C]//Proceedings of the 14th International Conference on Information Fusion. Piscataway,NJ,USA: IEEE,2011: 5977681.

[13] HAN Deqiang,DEZERT J,YANG Yi. Belief interval-based distance measures in the theory of belief functions [J]. IEEE Transactions on Systems Man & Cybernetics Systems,2016,99: 1-18.

[14] SMETS P. Data fusion in the transferable belief model [C]// Proceedings of the 3rd International Conference on Information Fusion. Piscataway,NJ,USA: IEEE Computer Society,2000: 21-33.

[15] 杨艺,韩德强,韩崇昭. 基于多准则排序融合的证据组合方法 [J]. 自动化学报,2012,38(5): 823-831.

YANG Yi,HAN Deqiang,HAN Chongzhao. Evidence combination based on multi-criteria rank-level fusion [J]. Acta Automatica Sinica,2012,38(5): 823-831.

[16] 杨风暴,王肖霞. D-S证据理论的冲突证据合成方法 [M]. 北京: 国防工业出版社,2010,70-71.

[17] ELOUEDI Z,MELLOULI K,SMETS P. Assessing sensor reliability for multisensor data fusion within the transferable belief model [J]. IEEE Transactions on Systems Man & Cybernetics: Part B Cybernetics,2004,34(1): 782-787.

[18] 邢清华,刘付显. 基于证据折扣优化的冲突证据组合方法 [J]. 系统工程与电子技术,2009,31(5): 1158-1161.

XING Qinghua,LIU Fuxian. New combination rule of conflict evidence based on optimized evidence discount [J]. Systems Engineering & Electronics,2009,31(5): 1158-1161.

[19] 付耀文,贾宇平,杨威,等. 传感器动态可靠性评估与证据折扣 [J]. 系统工程与电子技术,2012,34(1): 212-216.

FU Yaowen,JIA Yuping,YANG Wei,et al. Sensor dynamic reliability evaluation and evidence discount [J]. Systems Engineering & Electronics,2012,34(1): 212-216.

[20] DE FERIET J K. Interpretation of membership functions of fuzzy sets in terms of plausibility and belief [J]. Fuzzy Information and Decision Processes,1982(1): 93-98.

[本刊相关文献链接]

魏港明,刘真,李林峰,等.加入用户对项目属性偏好的奇异值分解推荐算法.2018,52(5):101-107.[doi:10.7652/xjtuxb201805015]

蒋逸飞,张俊,何勇,等.面向裂纹扩展的连结型刚体-弹簧离散元模型.2018,52(4):48-54.[doi:10.7652/xjtuxb201804 007]

赵振冲,王晓丹.引入拒识的最小风险弹道目标识别.2018,52(4):132-138.[doi:10.7652/xjtuxb201804019]

卫博雅,寿业航,蒋雯.一种可视化的加权平均信息融合方法.2018,52(4):145-149.[doi:10.7652/xjtuxb201804021]

姜洪权,王岗,高建民,等.一种适用于高维非线性特征数据的聚类算法及应用.2017,51(12):49-55.[doi:10.7652/xjtuxb201712008]

周亚东,陈凯悦,冷俊园,等.软件定义网络流表溢出脆弱性分析及防御方法.2017,51(10):53-58.[doi:10.7652/xjtuxb 201710009]