解读试题 拓展思维 提升能力——2017年温州中考第21题评析与变式

浙江省温州市教育教学研究院

章才岔 (邮编：325000)浙江省温州市第十九中学 何 萍 (邮编：230001)

遵循《课标》评价要求，即“评价的主要目的是全面了解学生数学学习的过程和结果，激励学生学习和改进教师教学”，初中毕业升学考试命题将“能力立意命制试题”作为基本的命题原则，以学生的发展作为命题的基本出发点，使试题不仅仅是体现出学生对基本知识、基本技能的掌握情况，更能体现出学生在已积累的数学活动经验上的发展情况，在过程中考查学生，让学生经历发现、分析及解决问题的过程，让学生有主动探索的意识，使考查点最终落脚在创新意识的培养．笔者以自己命制的2017年温州市中考数学第21题为例，结合试卷答题情况，以飨读者．

1 试题呈现

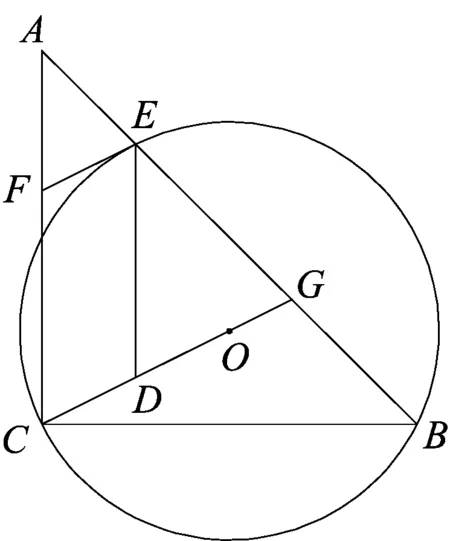
图1

如图1，在△ABC中，AC=BC，∠ACB=90°，⊙O(圆心O在△ABC内部)经过B、C两点，交AB于点E，过点E作⊙O的切线交AC于点F，延长CO交AB于点G，作ED∥AC交CG于点D.

(1)求证：四边形CDEF是平行四边形．

(2)若BC=3，tan∠DEF=2，求BG的值．

2 试题特色

2.1 考查核心知识，关注“逻辑推理”

本题以圆、三角形、平行四边形为背景，考查了特殊图形(圆、等腰三角形、直角三角形、平行四边形、相切)的主要性质、三角函数等初中数学核心知识．要求学生借助图形，逐步推导梳理有用的结论，找到正确的思考路径．全面有效地考查学生图形分析能力，获取信息与处理能力，从不同程度上反映了学生的解题基本活动经验，是否能有证据、有条理、合乎逻辑的思维，既重视“四基”的考查，又关注“逻辑推理”核心素养的考核．

2.2 难度合理，信度与区分度高

本题满分10分，每小题5分．从整体平均分来看，达到5.687分，其中第(1)小题平均分为3.429分，第(2)小题平均分为2.258分，作为中等难度的题目，其难度值相对合理．从网上阅卷分析统计来看，各县市区的信度与区分度均较高，且两小题的难度上具有一定的层次性，既具备了学业考试考查四基的功能，又兼顾了升学考试的选拔甄别功能．

2.3 解题入口宽，方法多样

本题嵌套基本图形、特殊图形，图形相关性质借助不同图形载体相互转化，解题入口宽，方法多样，适合不同层次学生用不同方法求解．第(1)小题可以通过两组对边分别平行证明，也可以通过一组对边平行且相等来证，根据在圆中证平行线或线段相等的不同途径，该小题至少有十种以上方法．第(2)小题有多种方法构造直角三角形，进行条件“tan∠DEF=2”的转化，据不完全统计，至少有五种以上方法(详见典型解法)．

2.4 背景源于教材，熟悉中凸显能力

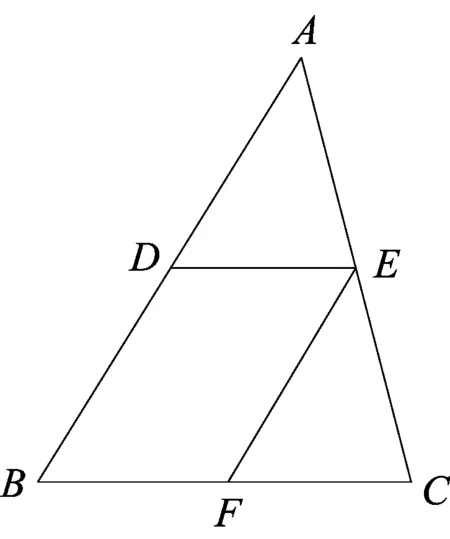
图2

本题图形源自浙教版教材八下第四章的两个作业题，“4.4平行四边形的判定定理(1)”作业题第3题，“4.5三角形的中位线”作业题第2题(图2)．原题条件均是给出中点或中位线证平行四边形．命制时，改变原条件中位线，添加特殊三角形、圆以及相切等条件．一方面，学生对于这样的图形非常熟悉，解题时有亲切感，另一方面，由于增加了特殊三角形、圆、相切，新题有别于各类模拟试题，有利于实现中考试题公平选拔功能，凸显学生逻辑推理能力.

3 典型解法

3.1 问题(1)的典型解法

思路1利用同旁内角互补证平行.

图3

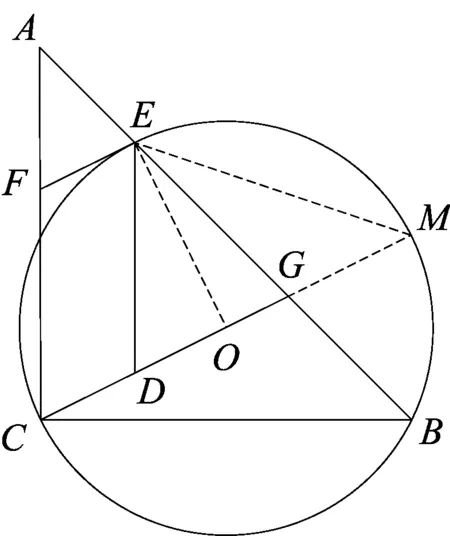
图4

解法1如图3，连结OE．可求得∠COE=90°，∠FEO=90°，利用∠COE+∠FEO=180°，得EF∥CO，可证四边形CDEF是平行四边形．

解法2如图4，延长CG交⊙O于点M，连结EM、OE，根据∠M=∠B=45°，OE=OM，可得∠OEM=∠M=45°，则∠COE=90°，则EF∥CO.

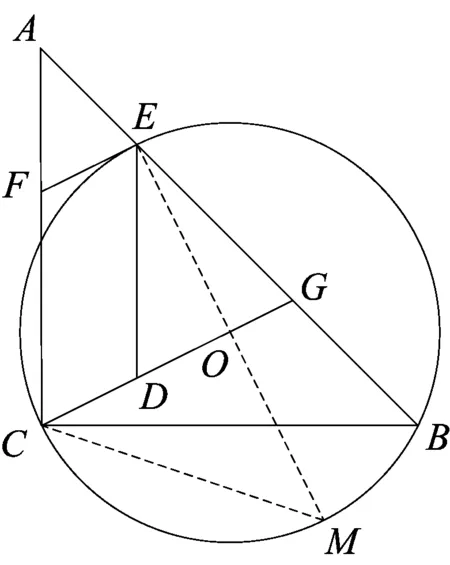
图5

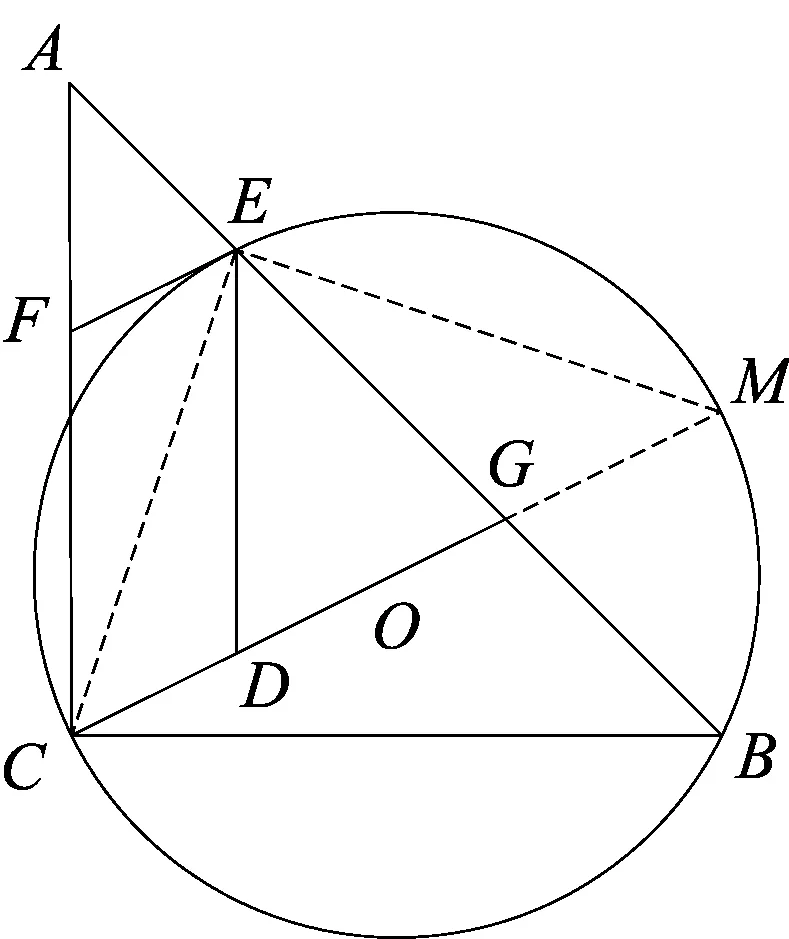
图6

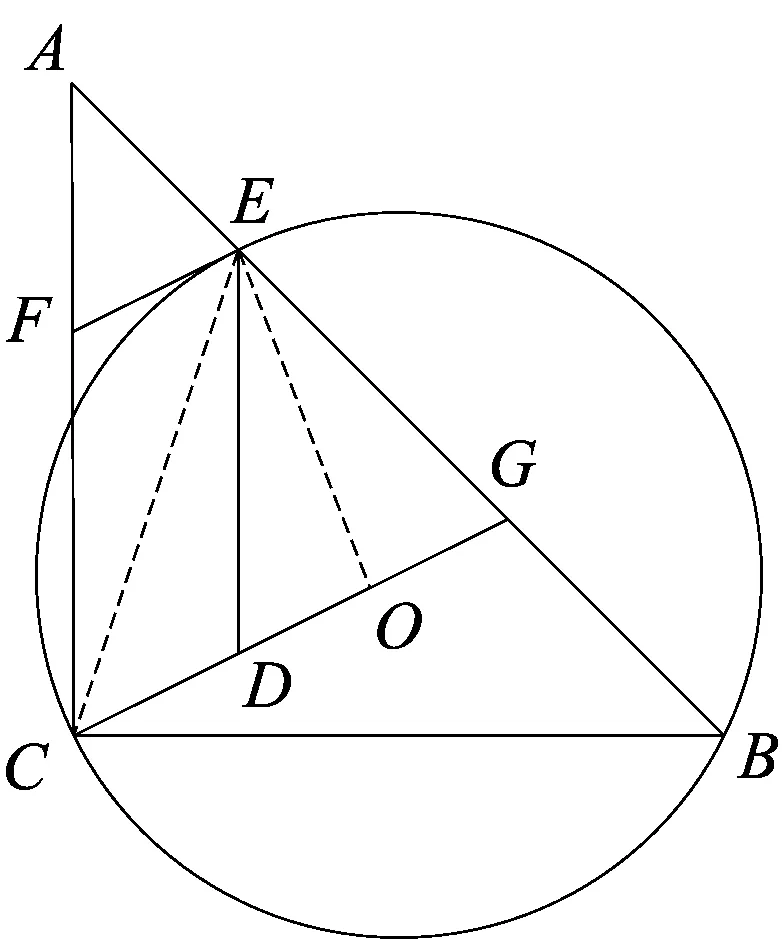
图7

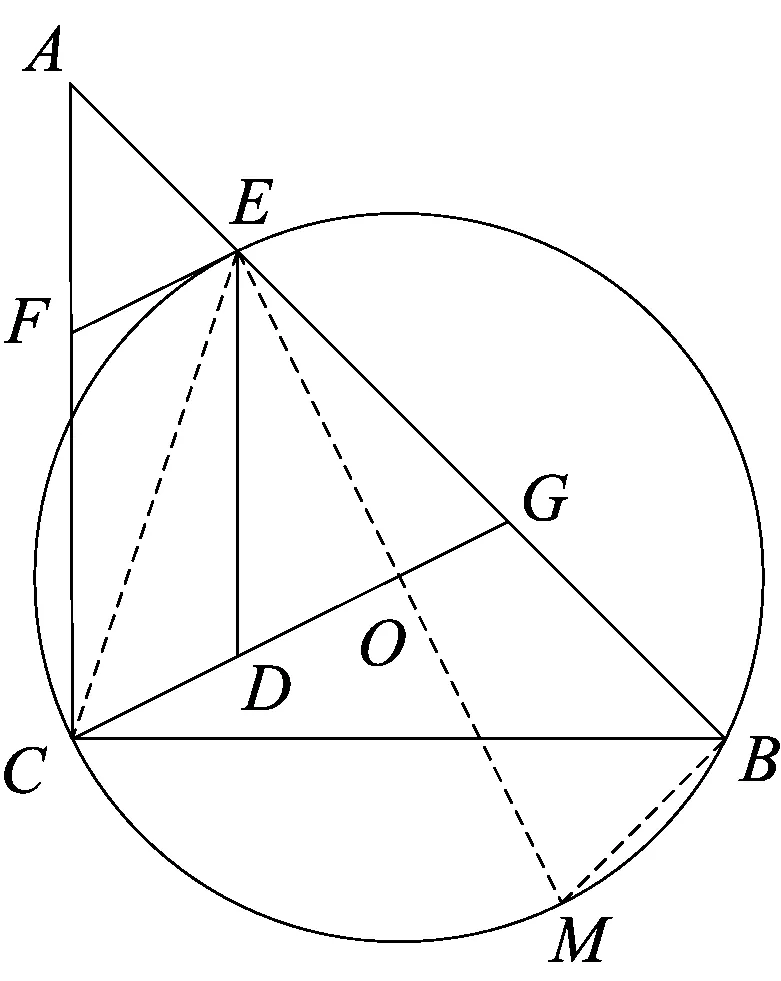
图8

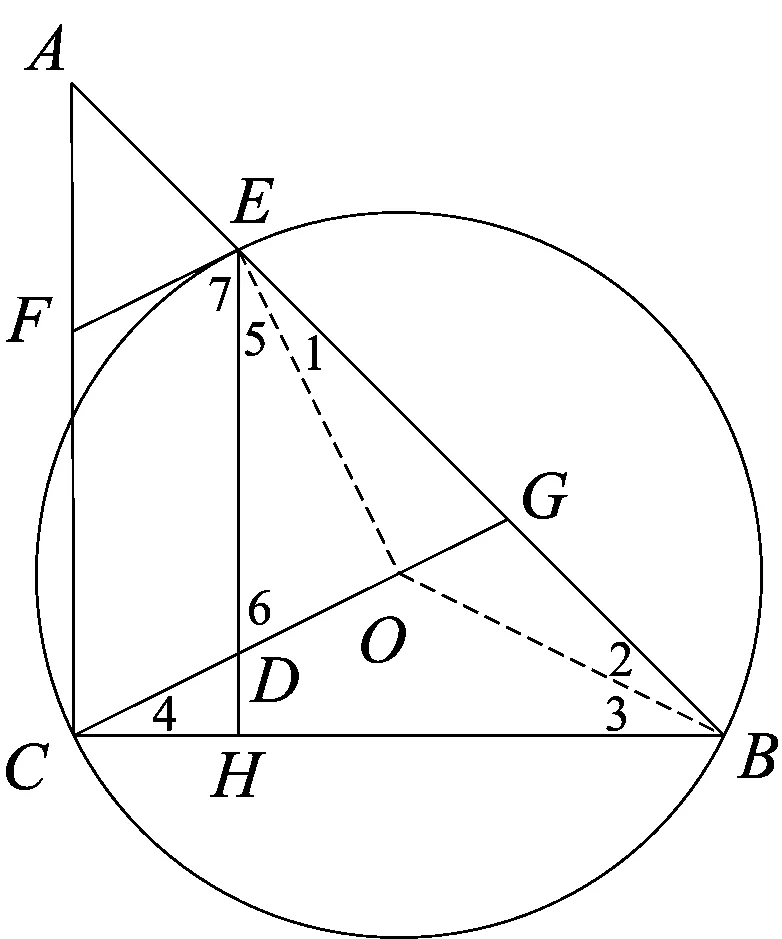
图9

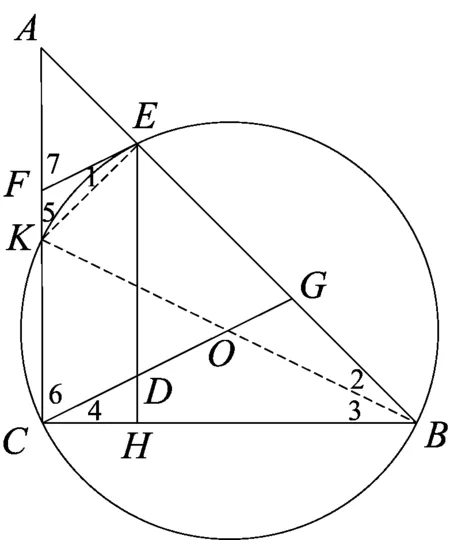
图10

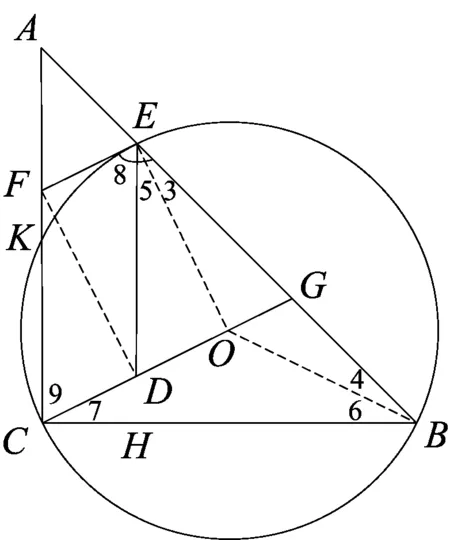
图11

解法3如图5，连结EO并延长交⊙O于点M，连结CM，同理可得∠OCM=∠M=45°，则∠COE=90°，则EF∥CO.

思路2利用内错角相等证平行.

解法4如图6，连结CE，延长CO交⊙O于点M，连结EM，可得∠FEC=∠B=∠M=45°，由∠CEM=90°，得∠ECM=45°，则EF∥CM.可证四边形EFCD为平行四边形．

解法5如图7，连结OE，可得∠CEO=45°，则∠OCE=∠OEC=45°，∠FEC=∠OCE，则EF∥OC.

解法6如图8，连结EO并延长交⊙O于点M，连结CE，可得∠CBM=45°，∠CEM=45°，则∠OCE=∠OEC=45°，由∠CEF=45°，得∠FEC=∠OCE，则EF∥OC.

解法7如图9，连结OE、OB，由∠1=∠2，∠1+∠5=∠2+∠3=45°，得∠3=∠5，则∠4=∠5，可得∠7=∠CDH=∠6，则EF∥CD.

思路3利用同位角相等证平行.

解法8：如图10，连结BK、EK，易知BK为直径，令∠2=x，∠3=y，则x+y=45°，根据圆内接四边形性质及切线的性质，得∠5=∠ABC=∠2+∠3=x+y=45°，∠1=∠2=x，则∠7=∠5+∠1=45°+x.因为∠6=90°-∠4=90°-∠3=90°-y=90°-(45°-x)= 45°+x，则∠7=∠6，则EF∥CD.

解法9如图10，证明∠AEF=∠AGC，则EF∥CD.

思路4证明一组对边相等．

解法10如图11，连结OE、OB、DF，依次求出∠B=∠DEG，∠3=∠4，∠5=∠6，则∠8=∠9.根据∠DFC=∠FDE，FD=FD，可得

△CDF≌△FED，则CF=ED.可证四边形EFCD为平行四边形．

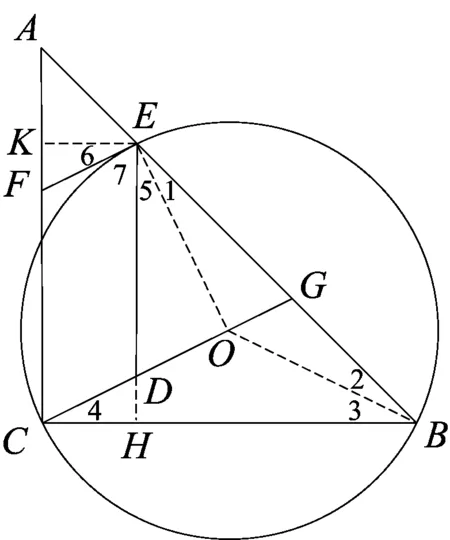
图12

解法11如图12，作EK⊥AC于点K，连结OB、OE，可得∠6=∠5.由解法7可得∠4=∠5，则∠4=∠6.可证△EFK≌△CDH.在全等之后，可以通过另一组对边平行且相等，或通过两组对边分别相等，或通过定义等方法，均可证明四边形CDEF为平行四边形.

思路5证明两组对边分别相等.

解法12如图12，根据思路2可知△CDF≌△FED，则CF=ED，EF=CD，则四边形EFCD为平行四边形．

3.2 问题(2)的典型解法

图13

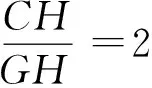
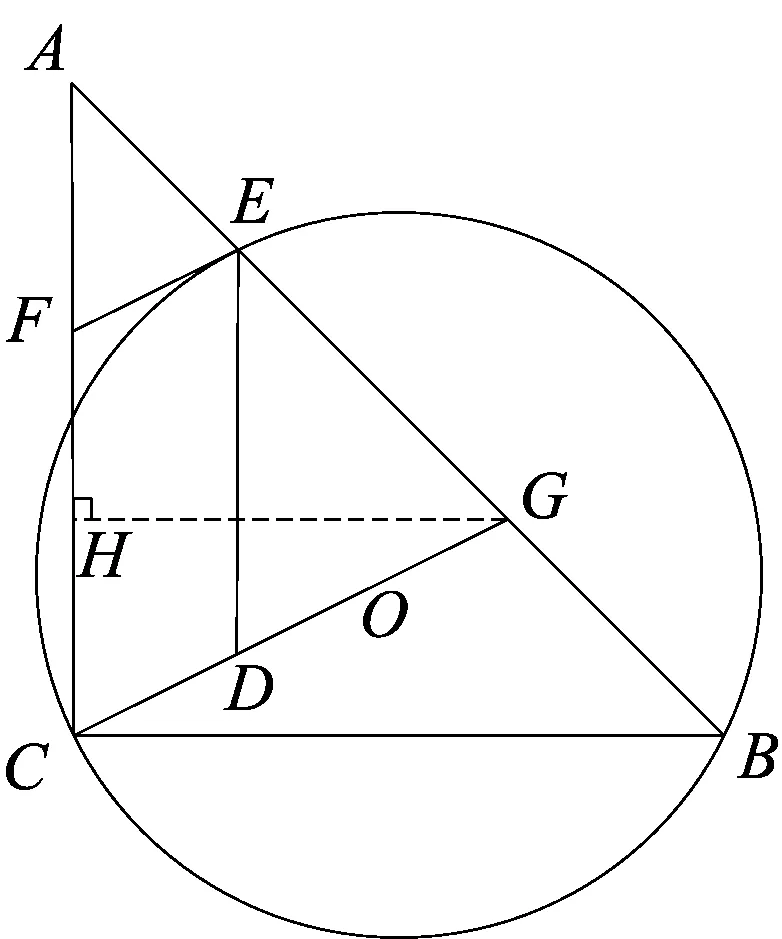
图14

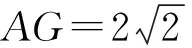
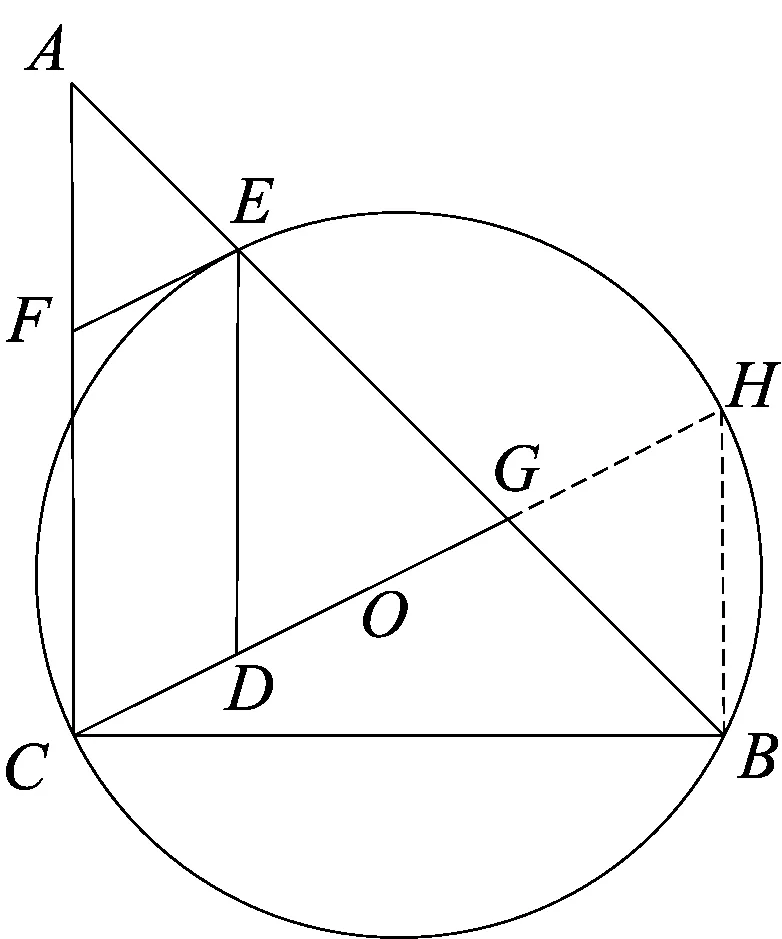
图15

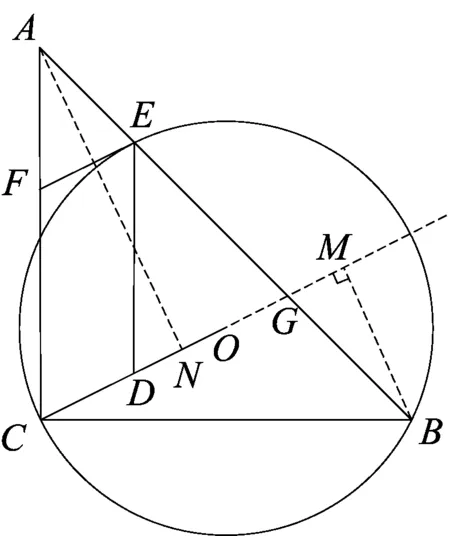
图16

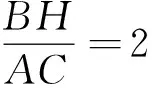
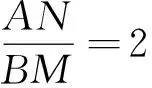
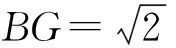
4 教学导向分析

4.1 立足核心知识，把握思想方法

数学教材的育智与全面育人的因素，是蕴含在教材之中，以凝聚的、物化的形式存在着的．通过对教材中的问题、图形进行改编，创造性地开发、利用教材资源，是中考命题的来源之一．改编源自典型，切合学情，符合数学研究本质，揭示数学核心知识之间的内在联系．章建跃教授指出：“构建反映数学内在发展逻辑、符合学生数学认知规律的中学数学核心概念、思想方法结构体系，并使核心概念、思想方法在数学课堂中得到落实，是提高数学课堂教学质量和效益的突破口，同时也是数学课堂教学改革的抓手．”因此，站在系统的角度，立足教材，关注《课标》核心知识的地位和作用，运用初中数学知识体系的整体观思想，加强知识间的联系和再生性，重视数学思想的教学．

本题作为初中毕业学业升学考试试题，有其功能与定位，考虑到整卷的题型结构、知识分布、难度设计、效度信度等因素，命题组最终选择了证明平行四边形与计算线段BG的长度，但作为源自教材的一个几何问题，实现其教学功能最大化，本题还有其他变化与拓展，供同行参考交流．

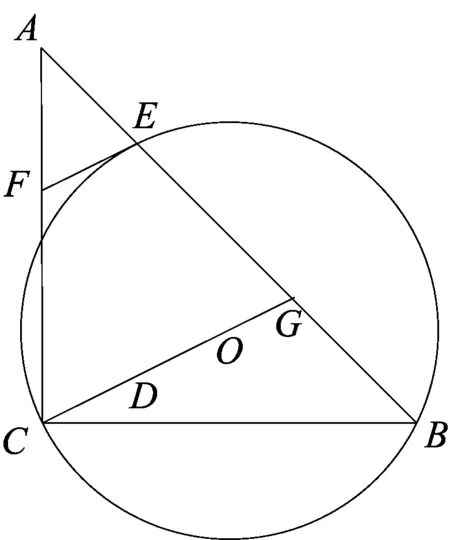
图17

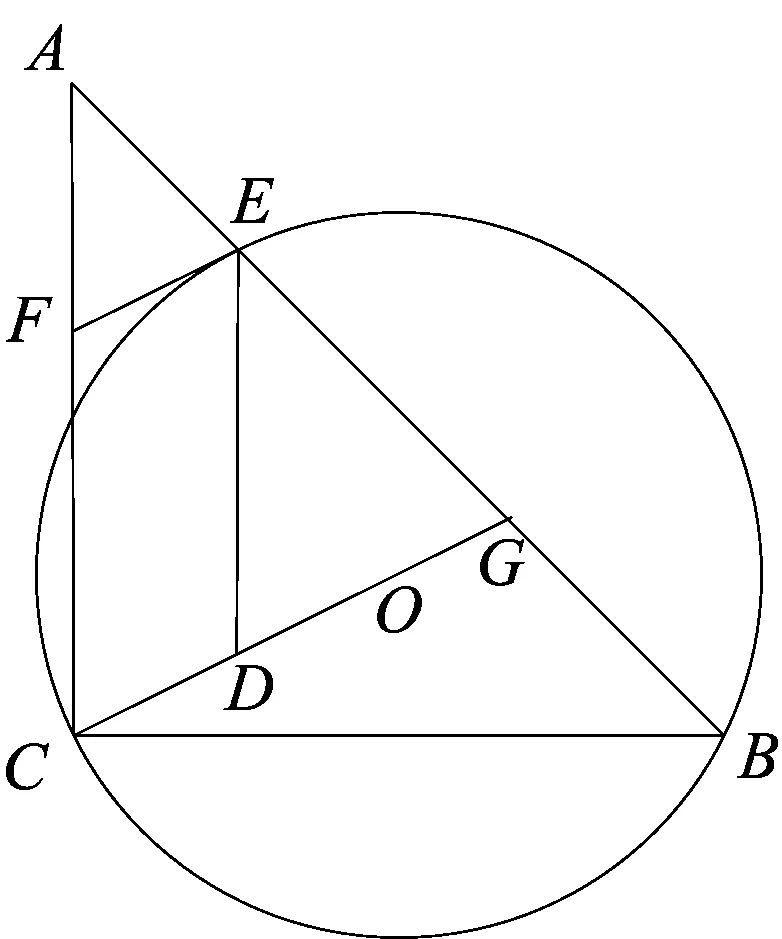
图18

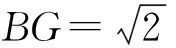
图19

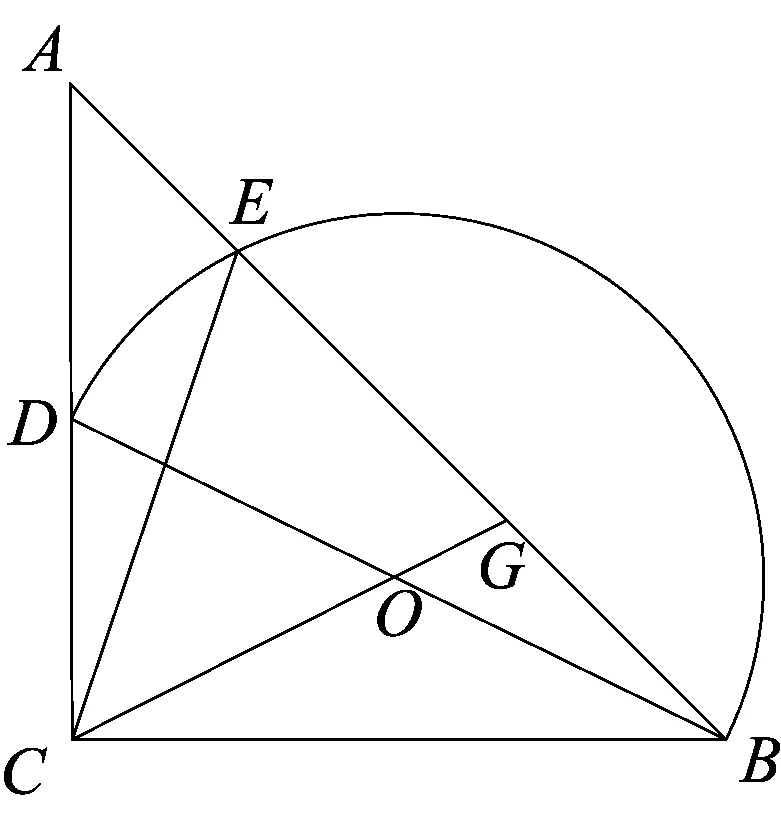
图20

变式四如图20，在△ABC中，AC=BC，∠ACB=90°，点D在AC上，以BD为直径作半圆O交AB于点E，连结CO并延长交AB于点G.(1)求证：AE2+BG2=EG2；(2)当BD平分∠ABC，CD=1时，求△CEG的面积.

4.2 注重“通性通法”，突出数学核心素养

中考命题比较原本，要求蕴含某些新意，具有形式新、内容新、解法新等特点，具有创新性也正是中考命题的魅力所在．形式新包括问题的情境新、结构新、表述新等；内容新主要体现在改编后的问题条件系统和结论系统的更新变化，包括元素限定、构件模型、结构关联、考查对象、设问层次、呈现方式等的变化；解法新是因为内容的变化可能致使问题解决的方法发生变化．所以，教师要摆脱题海战术演练，教会学生“通性通法”的策略性知识．如，解决几何问题的一个基本策略就是：首先要认真分析条件，将条件与相关“基本图形”结合起来，利用这个“基本图形”的性质，获得相应的结论．有时图形中不一定有与条件匹配的“基本图形”，这时还需要联想相关知识作辅助线构造出相关的“基本图形”，再利用这个“基本图形”的性质，获得相应的结论，从而达到解决问题的目的．

初中阶段的数学知识大多属于本源性知识和派生性知识，学生的学习往往采用“感性认识——理性认识——实践”的方法，而高中阶段则基本采取“已知理性认识——新的理性认识——实践”的方法．因此，初中阶段若不及时巩固总结，寻找知识间的联系，只是赶抄作业、乱套题型，对概念法则公式定理一知半解，机械记忆模仿，结果将很难快速适应高中的学习．本题意在突破这一考查定势，综合多个知识，凸显能力考查，引导师生关注逻辑推理，提前为初高衔接做好准备．

《课标》“四基”中提出了“基本活动经验”，即重视学生思维活动经验的积累，“四能”中提出了“发现和提出问题”，即重视学生创新能力的培养，这些应该在教学中有所体现．关注数学核心素养，重视逻辑推理、数学建模、数学抽象、直观想象的过程教学，丰富学生思维的活动经验，有利于创新能力和可持续发展的培养．

1 林崇德．21世纪学生发展核心素养研究[M].北京：北京师范大学出版社

2 李庚南．自学·议论·引导教学论[M].北京：人民教育出版社

3 蔡小雄．更高更妙的高中数学一题多解与一题多变[M].杭州：浙江大学出版社

4 教育部制定．普通高中数学课程标准(实验)[M].北京：人民教育出版社．2016

5 教育部制定．义务教育数学课程标准(2011年版)． 北京师范大学出版社

6 潘超.试论数学问题改编的方式和要求[J].数学通报，2014(6)：21-24