锁定、解剖钢板固定SandersⅡ跟骨骨折稳定性的有限元分析*

何凯张金花杨物鹏付苏吴建群高晓宇

跟骨具有较为复杂的几何形态和内部结构，跟骨骨折为临床常见病和多发病[1,2]，多为关节内骨折，因此其治疗手段选择显得至关重要[3]。多数骨科医生认为Sanders分型对跟骨骨折治疗的选择及预后的判断有较高的临床价值，对于SandersⅡ型跟骨骨折，最适当的治疗方案不定[4,5]。SandersⅡ型跟骨骨折手术治疗的疗效优于非手术治疗，手术的内固定常规使用锁定钢板和解剖钢板，但是二者的治疗效果存在争议。除了需要考虑骨折分型、周围软组织条件等因素外[2,6,7]，还应从二者治疗跟骨骨折后所获得的稳定性效果考虑，因为较差的稳定性可能会导致并发症[8-11]，包括感染或骨折不愈合，因此选择最佳的治疗方案需要比较不同内固定的稳定性。有限元分析技术能够较方便地模拟跟骨骨折复杂的位移、应力和形变等情况，所以，锁定钢板和解剖钢板内固定系统治疗SandersⅡ型跟骨骨折的生物力学研究显得尤为必要。

1 材料与方法

1.1 对象

选择一名健康24岁男性志愿者，身高178 cm，体重70 kg，X射线检查未见足跟部的畸形及退变，该志愿者同意并接受该实验过程，并已签署实验知情同意书。对其左足踝部的中立非负重位跟骨螺旋CT，层厚1 mm。

1.2 设备

美国GE公司生产的Lightspeed16层螺旋CT。

1.3 软件

Dassault Systemes S.A公司生产的 SolidWorks软件，Materialise公司生产的MiMics11.0三维重建软件，美国AN-sys公司的ANSYS 12.0有限元分析软件，美国Geomagic的三维模型处理软件。

1.4 方法

1.4.1 跟骨三维模型重建

将志愿者的472张足部横断面 CT原始数据以 Dicom格式导入 Mimics 11.0软件，Mimics软件中软组织和骨骼具有不同的灰度值对灰度值进行分割，调整阈值，建立MIMICS的初步踝关节模型，以STL格式的三维模型数据输出结果[12,13]。将结果输入到Geomagic Studio软件，对初步建立的踝关节模型进行降噪、平滑、曲面拟合等处理，从而生成实体零件（见图1）。

图1，初步跟骨模型（Mimics软件）；平滑跟骨模型（Geomagic Studio软件）（彩图见插页）。

1.4.2 Sanders II型跟骨骨折三维模型建立

将已经建立的跟骨的三维模型，导入Solidworks软件中进行Sanders II型划分骨折模型切割处理。在跟骨模型冠状面上选择跟骨后距关节面最宽处，平均划分为三等分，1/3处和2/3处标记为A、B，C是距骨下边线，沿后关节面做三条平行线，建立3种骨折模型。即骨折线模型三种类型（A，B或C）（见图2）。骨折不同片段之间设计为完整的骨折平面模型和摩擦系数为0.2。

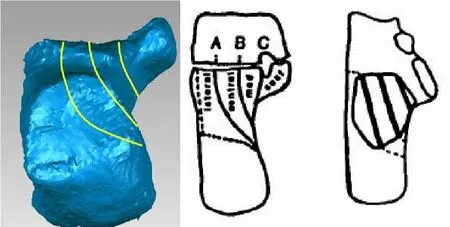
图2，建立Sanders II型跟骨骨折线模型。

1.4.3 跟骨骨折内固定三维模型建立

利用了天远三维扫描仪对跟骨锁定及"Y"解剖钢板、相关尺寸螺钉进行相对高精度扫描，制作相关三维CAD模型。根据跟骨钢板和螺钉使用说明，将锁定钢板及"Y"解剖钢板分别植入Sanders II型跟骨骨折模型，共建立6组模型，最后导入ANSYS软件中进行有限元分析（见图3）。

图3，跟骨骨折内固定物模型建立（彩图见插页）。（左：跟骨解剖钢板植入，右：跟骨锁定钢板植入）。

1.4.4 Sanders II型跟骨骨折内固定模型材料属性、施加负荷、边界条件

⑴材料属性赋值：钢板和螺钉的材料选择为钛质，骨质采用均质同向的线性模型[14]（见表1）。

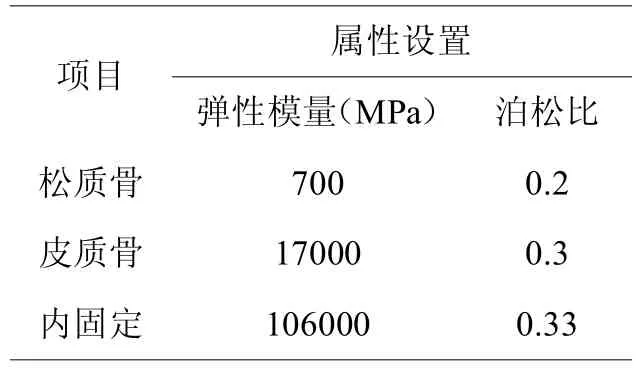
表1，Sanders II型跟骨骨折内固定模型材料属性

⑵载荷的施加设置：建立坐标轴，即脚趾指向脚跟为Y轴、踝关节外侧指向内侧为 X轴、足跟向上指向膝关节为Z轴，XY平面平行于足底平面。跟骨中立位置加载：在ANSYS软件页面上，固定跟骰关节面、跟骨与地面接触区域，总计施加约不同方向的500 N力学刺激[15-17]：前中距关节面82.5 N，后距关节面249.5 N，跟腱附着处137.5 N。

⑶设定如下评价标准，保证实验的顺利完成：骨折块间的位移＞150 m会出现骨折端不稳定。跟骨周围骨质剪切应力＞56 MPa会出现螺钉松动。当内固定物表面 von Mises应力＞450 MPa会出现钢板不可逆性形变，而＞600 MPa会出现钢板断裂[18]。

2 结果

2.1 有限元分析Sanders II型跟骨骨折内固定模型结果对比

对于Sanders II型各亚型跟骨骨折内固定模型，两组的骨折块应力峰值和内固定应力峰值均位于合理范围内，锁定钢板组的内固定应力峰值＜解剖钢板组，解剖钢板组的跟骨应力峰值＜锁定钢板组（见表3，4），对于Sanders IIA、IIB型模型，解剖钢板固定骨折块移位程度和骨折线相对移位程度明显＞锁定钢板，Sanders IIC型模型中两者相对移位的数据相近（见表2，图4），综上所述分析说明锁定钢板固定相对于解剖钢板更为稳定、可靠，而解剖钢板组更多应力集中于内固定物上（见图5）。

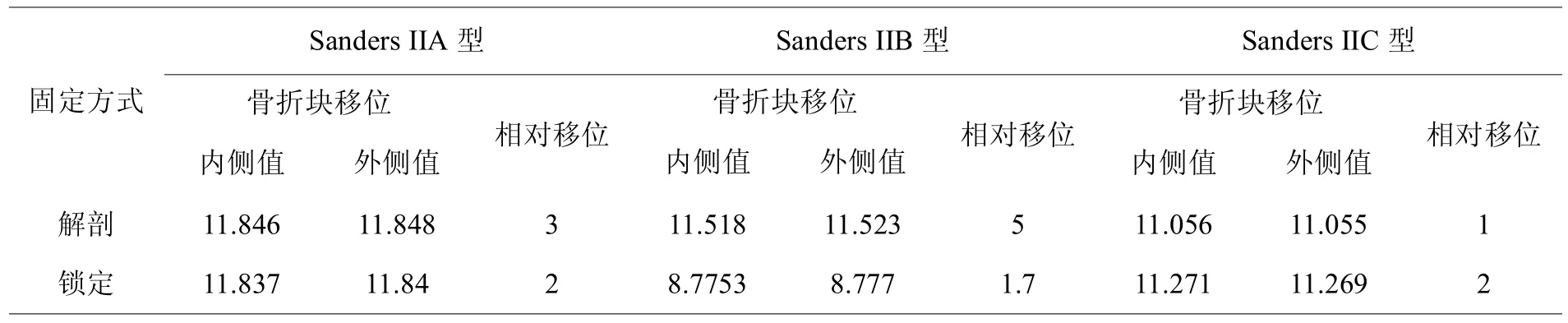
表2，锁定钢板和解剖钢板固定Sanders II型跟骨骨折块移位、相对移位（ m）

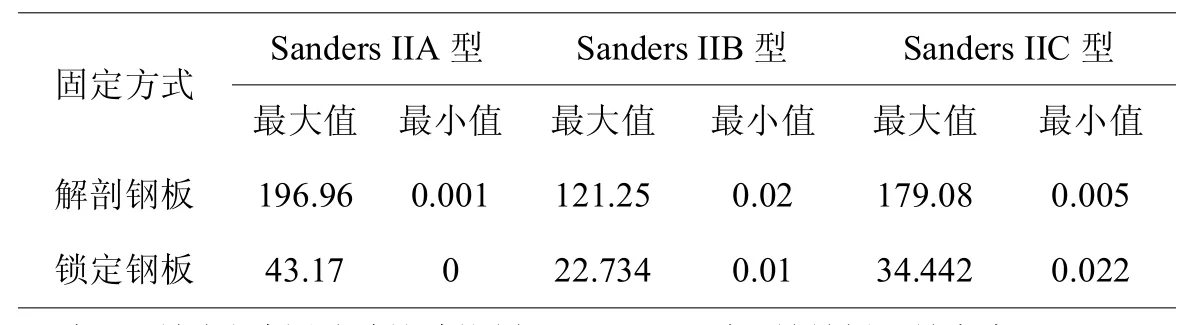
表3，锁定钢板和解剖钢板固定Sanders II型跟骨骨折内固定应力（MPa）

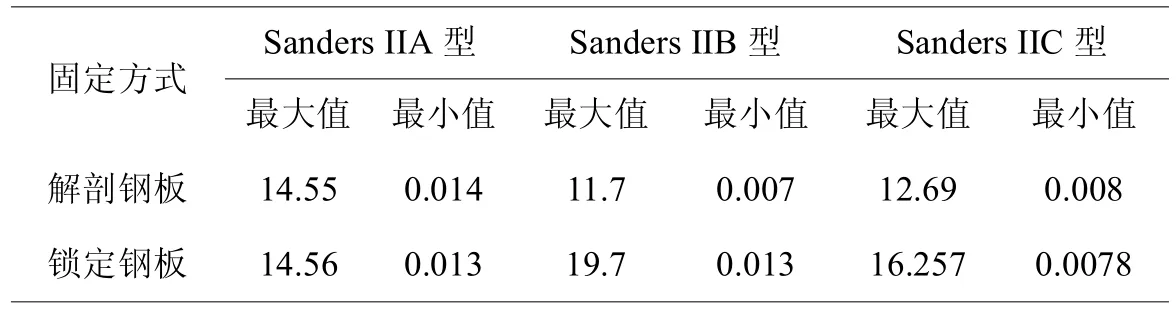
表4，锁定钢板和解剖钢板固定Sanders II型跟骨骨折跟骨应力（MPa）

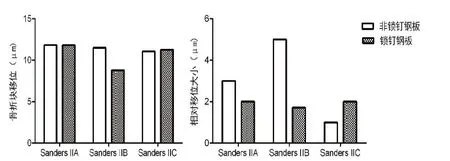
图4，锁定钢板和解剖钢板固定不同Sanders II型跟骨骨折的骨折块移位程度对比。

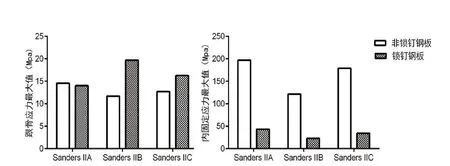
图5，Sanders II型跟骨骨折固定物植入模型钢板内固定应力分布，上中下三排分别为Sanders IIA、IIB、IIC跟骨骨折内固定及跟骨应力分分布情况，第一和第三例分别为锁定钢板和解剖钢板固定后钢板应力分布、第二例和第四例分别为锁定钢板和解剖钢板固定后跟骨的应力分布（彩图见插页）。

3 讨论

大部分跟骨关节外骨折可以通过保守治疗的方法得到较好的疗效，移位的关节内骨折可导致一系列问题，最终造成足部功能障碍[3]，目前主要治疗方式有切开复位的锁定钢板和解剖钢板内固定，而内固定所获得的稳定性在骨折预后中至关重要[11]。本实验通过有限元分析方法，对锁定钢板、解剖钢板固定的Sanders II型跟骨内固定骨折模型进行力学稳定性研究发现，锁定钢板固定时骨折块移位程度和骨折相对移位程度显优于解剖钢板，但骨折线之间最大位移并没有明显差异，且都小于1mm（跟骨关节内骨折手术指征标准是骨折线分离或移位≥1 mm），由此说明两种固定方式对恢复关节面平整，预防距下关节塌陷、骨折移位等具有类似作用，为临床工作提供理论依据。

本实验有限元分析结果与以往文献报道的实验结果相似，对于Sanders IIA型、IIB型跟骨骨折，锁定钢板的固定效果明显优于解剖钢板[10,19,20]，Richter通过生物力学研究发现锁定钢板组更高的加载失效强度和低形变特征，提示锁定钢板的坚强程度高于解剖钢板[21]。Richter的骨折模型通过跟骨截骨制作完成，解剖螺钉组是三种不同钛板配合解剖螺钉，另一组是钛板配合锁定螺钉，实验发现锁定螺钉组的骨折移位程度小，说明锁定螺钉组稳定性优于解剖螺钉组。同样，Kienast等通过研究发现临床上应用锁定钢板，患者固定及预后效果更好[22]，说明比较不同的内固定的生物力学稳定性，锁定钢板更有优势，这些结果原因：跟骨多由松质骨构成，骨折后常伴有骨缺损，锁定钢板不依赖于骨与钢板之间的摩擦力提供稳定，而是通过与螺钉的锁定来实现成角稳定，此种固定机制使锁定螺钉的轴向负荷及抗拔强度远高于解剖钢板，对于骨质疏松的跟骨骨折有较好的把持力。

Sanders IIA与Sanders IIB骨折块移位程度和骨折线相对移位程度结果比较后提示（见表2）：Sanders IIB移位数值相比于Sanders IIA型跟骨骨折数据较大，B骨折线较A骨折线靠内侧，反映跟骨钢板外侧固定的稳定性变化特点。Sanders IIC型跟骨骨折模型，两组骨折块的移位程度相近，锁定钢板固定时的骨折移位程度要稍高于解剖钢板，这可能是由于钢板不同形态所导致。分析其原因可能是：打入载距突内的螺钉在解剖钢板固定时起到了更好的稳定性作用，解剖钢板螺钉对载距突起到拉力作用，图5可以观察到，解剖钢板打入载距突的螺钉承受了较高的应力，而锁定钢板打入载距突的螺钉承担应力成阶段性分布，提示其发挥作用的不同。解剖钢板及锁定钢板的内固定应力和跟骨应力分布均无明显集中现象，以跟骨钢板前部应力分布较大，提示可以改进此类钢板设计。

三维有限元分析在骨科领域应用比较广泛，是骨科生物力学研究的主要方法[23]，进行有限元分析的前提是建立真实有效的实验模型，Bouyssie J F等使用多项数字骨科有限元医学软件，证实骨组织形成三维模型所得到的结果与真实结果相一致[24]，因此本试验模型具有较高准确性、仿真性。但是目前没有对关节软骨建模的报道，我们通过多次测量减少由关节软骨引起的实验误差，由于关节软骨准确贴附于下关节面，而且小于2 mm，这样的误差是可以接受的，保证了实验的可靠性。

有限元分析虽然可以模拟复杂的人体足部情况，但仍有其局限性[25]：本实验较少考虑人体复杂的结构差异，仅靠CT数据建模；没有考虑动态人体足部变化情况[26]。因此，本实验是Sanders II型跟骨骨折内固定分析的初步研究，下一步可以进行尸体标本试验等内容来进行研究，进一步为临床治疗提供依据。

[1] Guerado E,Bertrand ML,Cano JR.Management of calcaneal fractures:what have we learnt over the years?[J].Injury,2012,43(10):1640-1650.

[2] Palmersheim K,Hines B,Olsen BL.Calcaneal fractures:update on current treatments[J].Clin Podiatr Med Surg,2012,29(2):205-220.

[3] Molloy AP,Lipscombe SJ.Hindfoot arthrodesis for management of bone loss following calcaneus fractures and nonunions[J].Foot Ankle Clin,2011,16(1):165-179.

[4] Sanders R,Vaupel Z,Erdogan M,et al.The Operative Treatment of Displaced Intra-articular Calcaneal Fractures(DIACFs):Long Term(10-20 years)Results in 108 Fracturesusing a Prognostic CT Classification[J].J Orthop Trauma,2014,28(10):551.

[5] Sanders R,Fortin P,DiPasquale T,et al.Operative treatment in 120 displaced intraarticular calcaneal fractures.Results using a prognostic computed tomography scan classification[J].Clin Orthop Relat Res,1993,290:87-95.

[6] Femino JE,Vaseenon T,Levin DA,et al.Modification of the sinus tarsi approach for open reduction and plate fixation of intra-articular calcaneus fractures:the limits of proximal extension based upon the vascular anatomy of the lateral calcaneal artery[J].Iowa Orthop J,2010,30:161-167.

[7] Hospodar P,Guzman C,Johnson P,et al.Treatment of displaced calcaneus fractures using a minimally invasive sinus tarsi approach[J].Orthopedics,2008,31(11):1112.

[8] Wallin KJ,Cozzetto D,Russell L,et al.Evidence-based rationale for percutaneous fixation technique of displaced intra-articular calcaneal fractures:a systematic review of clinical outcomes[J].J Foot Ankle Surg,2014,53(6):740-743.

[9] Hsu AR,Anderson RB,Cohen BE.Advances in Surgical Management of Intra-articular Calcaneus Fractures[J].J Am Acad Orthop Surg,2015,23(7):399-407.

[10]Redfern DJ,Oliveira ML,Campbell JT,et al.A biomechanical comparison of locking and nonlocking plates for the fixation of calcaneal fractures[J].Foot Ankle Int,2006,27(3):196-201.

[11]Mostafa MF,El-Adl G,Hassanin EY,et al.Surgical treatment of displaced intra-articular calcaneal fracture using a single small lateral approach[J].Strategies Trauma Limb Reconstr,2010,5(2):87-95.

[12]Wang H,Wang X,Chen W,et al.Biomechanical comparison of interspinous distraction device and facet screw fixation system on the motion of lumbar spine:a finite element analysis[J].Chin Med J(Engl),2014,127(11):2078-2084.

[13]Jia YW,Cheng LM,Yu GR,et al.A finite element analysis of the pelvic reconstruction using fibular transplantation fixed with four different rod-screw systems after type I resection[J].Chin Med J(Engl),2008,121(4):321-326.

[14]Gray HA,Zavatsky AB,Taddei F,et al.Experimental validation of a finite element model of a composite tibia[J].Proc Inst Mech Eng H,2007,221(3):315-324.

[15]郭宗慧，庞清江，刘江涛，等.载距突螺钉内固定治疗SandersⅡ型跟骨骨折的生物力学研究[J].中华骨科杂志，2013，33(4):331-335.

[16]黄海晶，王捷，马建雄，等.跟骨三维有限元模型的建立与静态分析[J].中华骨科杂志，2010，30(3):282-286.

[17]黄诸侯，李俊，陈日齐，等.跟骨三维有限元模型的建立及其骨折发生机制[J].中国骨伤，2012，25(2):97-101.

[18]Vajgel A,Camargo IB,Willmersdorf RB,et al.Comparative finite element analysis of the biomechanical stability of 2.0 fixation plates in atrophic mandibular fractures[J].J Oral Maxillofac Surg,2013,71(2):335-342.

[19]Illert T,Rammelt S,Drewes T,et al.Stability of locking and nonlocking plates in an osteoporotic calcaneal fracture model[J].Foot Ankle Int,2011,32(3):307-313.

[20]Blake MH,Owen JR,Sanford TS,et al.Biomechanical evaluation ofa locking and nonlocking reconstruction plate in an osteoporotic calcaneal fracture model[J].Foot Ankle Int,2011,32(4):432-436.

[21]Richter M,Gosling T,Zech S,et al.A comparison of plates with and without locking screws in a calcaneal fracture model[J].Foot Ankle Int,2005,26(4):309-319.

[22]Kienast B,Gille J,Queitsch C,et al.Early Weight Bearing of Calcaneal Fractures Treated by Intraoperative 3D-Fluoroscopy and Locked-Screw Plate Fixation[J].Open Orthop J,2009,3(1):69-74.

[23]王凯.三维有限元分析在骨科中的应用[J].生物骨科材料与临床研究，2013，10(01):31-34.

[24]Bouyssie JF,Bouyssie S,Sharrock P,et al.Stereolithographic models derived from x-ray computed tomography[J].Reproduction accuracy.Surg Radiol Anat,1997,19(3):193-199.

[25]沈超，娄玉建，王秀会.跟骨内翻畸形对踝关节应力变化三维有限元分析[J].生物骨科材料与临床研究，2018，15(01):5-7.

[26]Er MS,Verim O,Eroglu M,et al.Biomechanical evaluation of syndesmotic screw design via finite element analysis and Taguchi's method[J].J Am Podiatr Med Assoc,2015,105(1):14-21.