基于覆盖理论的铁路救援列车部署方案研究

汤霖，孟学雷，郭文博，尚蕾

(1. 兰州交通大学 交通运输学院，甘肃 兰州 730070；2. 兰州铁路局 兰州电务段，甘肃 兰州 730070)

中国铁路路网逐渐呈现出线路跨度大，运营里程长，路网结构复杂的特点。面对复杂的国土资源环境和线路运营环境，铁路突发事件频发。如何科学合理地部署铁路救援列车，对于增强铁路路网的鲁棒性，保障铁路运输高效稳定具有重要意义。铁路救援列车部署车站的选取，与基于覆盖模型的选址问题类似。其可视为是救援列车部署车站对需要救援线路的覆盖。关于基于覆盖模型选址问题，1964年Hakimi[1]就曾建立中值模型。1974年Church提出最大覆盖模型[2]，覆盖选址理论发展出集合覆盖、最大覆盖、P-中心问题、P-中位问题和 Weber问题等。2005年，Berman等[3]提出了“逐渐覆盖衰退函数”并将其引入到广义最大覆盖模型。2012年，Farahani等[4]在前人研究成果基础上系统全面地回顾了有关覆盖选址问题的模型，解决方法和应用方式。2015年，Brimberg等[5]对经典中位模型进行了改进，提出了位于覆盖距离之外情况下的距离惩罚系数的部分覆盖理论。基于覆盖问题的选址问题这几年在国内学者中也逐渐被重视，许多学者在此领域做出了许多工作。在运输领域，公路运输和物流方面的研究较多，WANG等[6]以火灾救援为研究背景，综合考虑多车种、单车种距离部分覆盖、单车种数量部分覆盖因素下的协同救火服务点的最大覆盖模型。Albert等[7]提出了基于求救需求对网络分区规划的方法，并运用基于拉格朗日松弛算法改进的算法对其理论研究进行验证。针对铁路应急救援设施选址问题的研究较少。吴艳华等[8]以集合覆盖模型为基础，结合中国铁路自身的特点，提出了铁路救援基地的层级网络理念，运用层次分析法、灰色关联分析等方法抽象出救援需求点。以救援基地建设成本最小和救援响应时间最短为目标函数建立模型并求解，但是该模型的覆盖对象为抽象出的离散救援点。在现实生活中，铁路突发事件往往具有很强的不确定性。救援需求点的评估工作难度大，准确性低。铁路救援列车部署车站对线路的覆盖以弧段方式覆盖更为准确。有关弧段覆盖模型的研究较少，1976年，Revelle等[9]提出了最大弧段覆盖模型。Berman等[10]2007在广义最大覆盖模型基础上改进了传统的弧段覆盖模型。2016年，Blanquero等[11]考虑到需求点连续分布于网络弧段，设施布设点也分布于网络弧段的情况建立覆盖模型。蔡文学等[12]结合覆盖衰退理论和弧段覆盖理论提出了覆盖衰退函数，通过设立救援距离衰退函数描述“覆盖水平”实现对弧段的连续覆盖。马云峰等[13]通过建立时间满意函数保障了救援的时效性和连续覆盖。本文结合铁路突发事件的特点，构建考虑时间满意度和弧段覆盖率的覆盖模型，在现有技术设备和既有的技术车站中部署救援列车，以实现救援列车部署车站对铁路沿线的救援覆盖，最后运用拉格朗日松弛算法求解覆盖模型。

1 铁路救援列车部署车站选择模型

铁路救援列车部署车站选择问题的实质是在一定范围内的备选车站中，选取若干车站作为救援列车的部署车站，形成部署方案，以期对尽可能大范围内的线路提供突发事件条件下的救援服务。铁路路网内的救援列车部署点对突发事件求救地点实施救援时，其救援能力往往受限于合理救援范围。本文结合救援的时效性等要求，运用覆盖理论，以车站合理救援范围的基本约束，以救援点覆盖率及救援时效性为优化目标，设计覆盖率函数及时间满意度函数，建立铁路救援列车部署车站选择模型。

1.1 模型假设

结合中国铁路路网实际运用现状，也为了合理优化计算规模，本文将对现有的中国铁路线路网进行一定的抽象处理并加以限定。

1) 对于无技术能力部署救援列车的车站被简化为线路，在路网中不再以节点的形式标出。2) 有能力部署救援列车部署的技术站作为抽象路网中的节点。3) 枢纽内有能力部署救援列车的技术站分布密集，但是将枢纽简化为一个节点，只能部署一次。枢纽内各技术站间救援列车如何选址不做详细区分。4) 节点对自身的救援能力均视为满意救援和完全覆盖。5) 模型中涉及到的救援距离仅指救援列车部署车站到救援地点之间的距离，不考虑救援列车在部署车站内的走行距离。6) 救援的时间仅考虑救援列车从部署车站出发至救援地点的纯运行时间，不考虑救援列车启动程序的时间消耗和救援列车在车站内走行的时间消耗。7) 复线铁路不对线路上下行做区分，节点车站之间只认为有一条无向边相连。8) 本文假设救援列车收到求救信号后始终以安全允许最大速度vmax=120 km/h的时速奔赴救援地点。9) 本文假设黄金救援时间为t1=30 min，合理救援时间为t2=2 h，黄金救援距离为r=60 km，合理救援距离为R=240 km。10) 模型考虑不同救援列车部署车站对救援线路的联合覆盖率，但是不考虑不同救援列车部署车站同时对同一线路的联合救援。

设G=(N, A)为经简化抽象之后的无方向铁路线路网络，N表示网络中的节点(经抽象处理后仅保留技术性车站，及对枢纽抽象后的车站)集合，A表示网络中的弧段(铁路线路)集合。I表示在无方向网络G中具备部署救援列车条件的车站的集合。j和 k分别为无方向网络G中的救援点所在的弧段l的两个端点，并以此来表示弧段 l。因为在模型中需要考虑覆盖的方向，所以在网络G中用弧段两端的节点来表示弧段。

1.2 模型基础

对模型中出现的变量描述如表1。

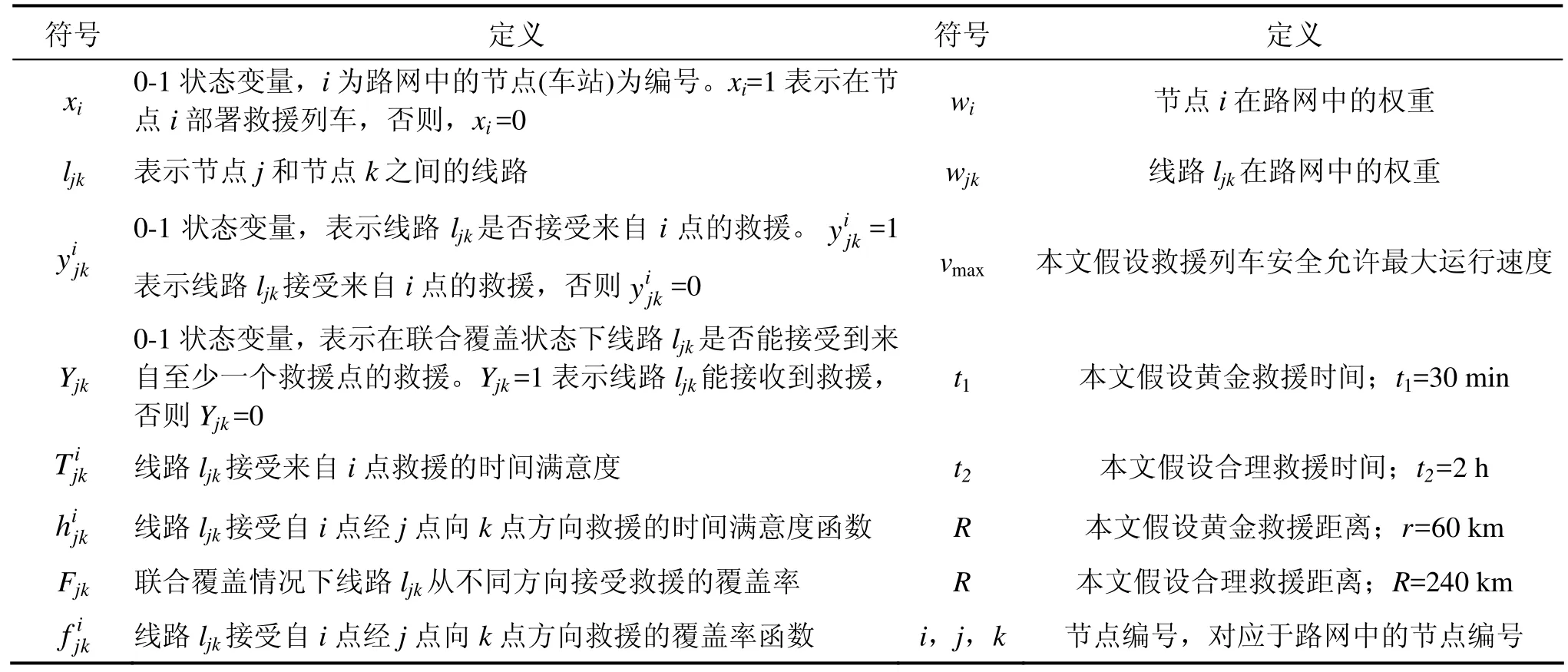
表1 模型符号定义表Table 1 Definition of model symbol

1.3 模型建立

考虑时间满意度的覆盖模型与最大覆盖率的数学模型整理如下：

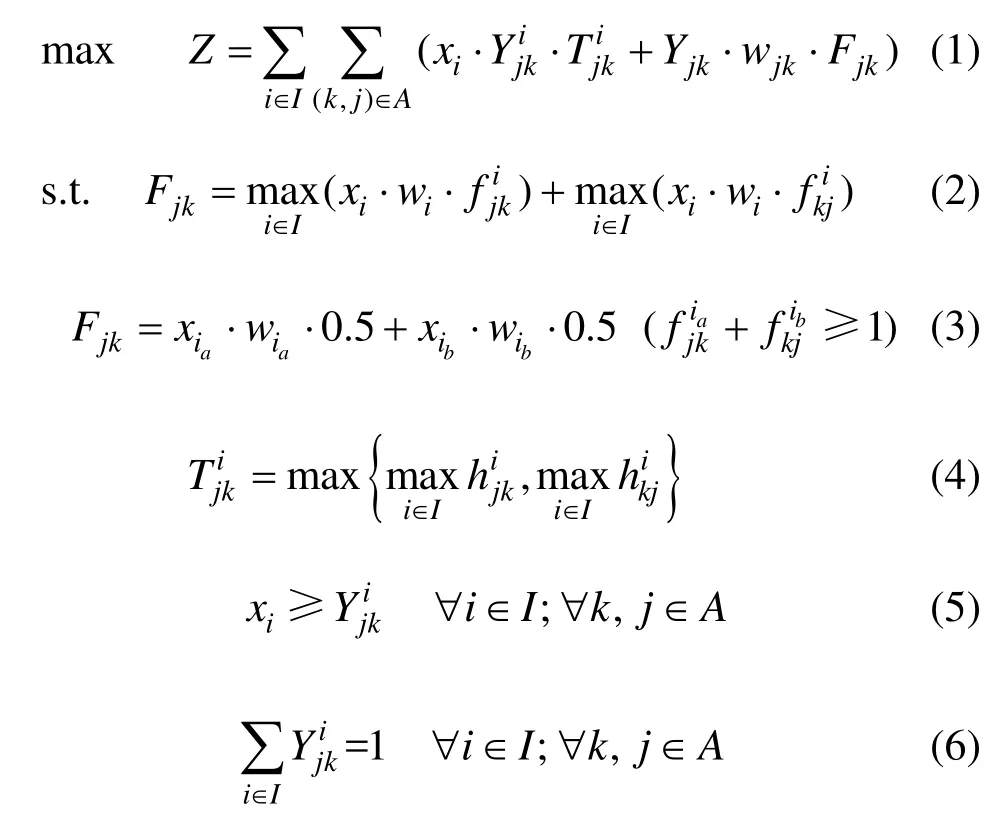
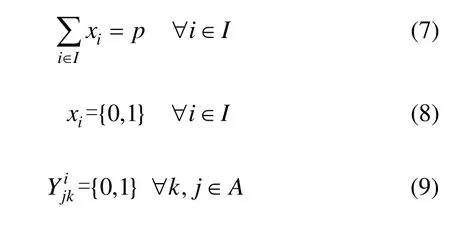
中国铁路路网呈现出复杂网络的特点。为了描述在铁路路网中某些铁路线路和车站在路网中的重要性，本文借鉴复杂网络理论中关于“介数”和“度”[14]的概念。以网络中经过该边的最短路径数目作为边的权重。将节点在网络中的度作为该节点的权重。分别将其赋予线路权重wjk和节点权重wi。

Fjk为救援列车部署车站对线路 ljk的联合覆盖率函数。当救援列车以固定的安全允许最大运行速度从车站赶赴求救地点，救援覆盖水平随着救援点与救援列车部署车站的距离增大而衰减。覆盖率函数为：

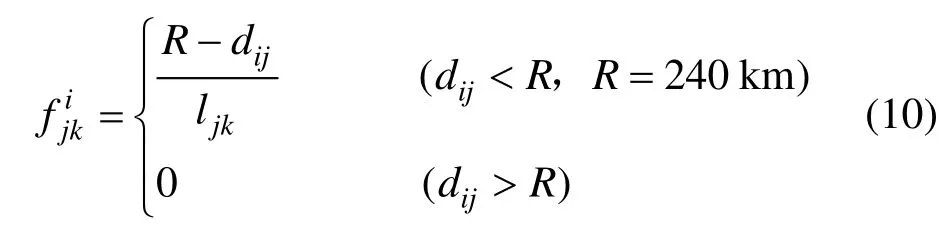
式(10)中的R为合理救援距离；djk为i站从j站向k站对线路ljk的救援点实施救援时，从i站到j站的距离；ljk为施救线路 ljk的长度；表示救援列车部署车站i从j站向k站对线路ljk的覆盖水平。同理可得为救援列车部署车站i从k站向j站对线路ljk的覆盖水平，如图1所示。

图1 覆盖率示意图Fig. 1 Simple map of coverage rate

关于约束条件式(2)和式(3)，线路 ljk可以被不同的救援列车部署车站i∈I从不同的方向进行联合覆盖的，其覆盖率从不同方向是可以联合的，但是同一方向的覆盖率只选取最大值，不考虑叠加。在如图2所示的覆盖环境下，从j站向k站对线路ljk进行覆盖的救援列车部署站中{i1, i2, i3}∈I选取其他覆盖值将不累加入。同理，从k站向j站对线路ljk进行覆盖的救援列车部署站中{i4, i5, i6}∈I选取最终联合覆盖率因此可得更普遍的模型约束条件式(2)。

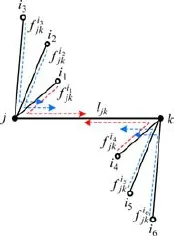
图2 双向联合覆盖示意图Fig. 2 Simple map of two-way combined covering

当联合覆盖出现联合覆盖率大于1的情况时。如图3所示，以类型Ⅰ为例：线路区段Δl即位于救援车站 i1的合理救援范围内，同时线路区段 Δl又位于救援车站i2的合理救援范围内。此时考虑节点权重时默认为联合覆盖节点各提供50%的覆盖，类型Ⅱ同理。因此可得约束条件式(3)。

图3 联合覆盖后出现重复覆盖情况示意图Fig. 3 Simple map of repeated coverage in combine covering

约束式(1)中，为救援列车部署车站 i对线路ljk实施救援的时间满意度函数。在不考虑联合救援的情况下，将接收i∈I中对线路ljk覆盖满意度最大的救援方向。如图4所示，以类型I为例，设时间满意函数，其中表示从i站经j站向线路ljk实施救援的时间满意度，表示从i站经k站向线路ljk实施救援的时间满意度，类型Ⅱ同理。因此可得约束条件式(4)。

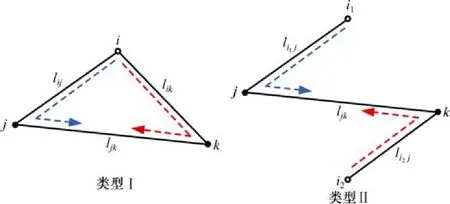
图4 基于时间满意函数覆盖示意图Fig. 4 Simple map of coverage based on time satisfaction function

时间满意度函数选取降高斯分布函数。因为，当模型受到救援列车部署成本限制致使个别需求救援线路的实际距离已超出合理救援覆盖距离时，其覆盖程度为 0，该点的救援满意度也将下降到一个极小值，但是即便如此也不能放弃对求救线路实施救援，随意时间满意度可以是极小值但是不能为0。时间满意函数如式(11)所示：

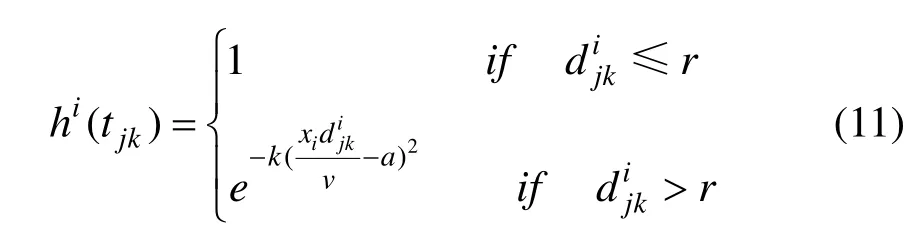
式(11)中为从i站经j站向线路ljk的求救点的距离；v为救援列车最大安全运行速度；a为最佳救援时间。k(k>0)为时间满意函数中的系数。系数k运用最小二乘法学习获得。

发生铁路突发事件的铁路线路 ljk将接收至少来自一个救援车站的救助。所以设置约束条件，如式(5)所示。当救援具体实施时，仅考虑单一救援列车部署车站对救援线路实施救援，故可得约束条件式(6)。基于对新建救援列车部署车站成本高的考虑，以及现有技术设备充分利用的角度出发，决策者可以在现有的技术站中根据各个铁路局(铁路公司)的实际能力选择救援列车部署车站的数量，因此，设置约束条件式(7)。约束式(8)和(9)中xi和是0-1状态变量，xi=1表示在救援列车部署车站集合I中的i点被选择部署救援列车，否则xi=0。=1则线路ljk上的突发事件点将接收来自部署在车站i的救援列车的救援，否则=0。

2 算法设计

有关覆盖模型的解决方法前人们尝试过分枝定界法，蚁群算法和贪婪算法等启发式算法，都得出了计算结果。Dantrakul等[15]尝试运用贪婪算法求解考虑设施构建成本和运输成本的P中位问题和P中心问题，并以实际算例验证了贪婪算法解决该问题的有效性。LAI等[16]提出了一种基于最小生成树问题最优解变形而改进的近似算法用以解决中位问题，通过与传统近似算法的比较证明了该算法解的有效性和优质性。其中拉格朗日松弛算法是解决集合覆盖问题的经典算法，SAIF等[17]设计了一种封闭式的表达式用以求解拉格朗日乘子，并将拉格朗日启发式算法嵌入到分枝定界法中用以求解设施选址问题。Kim 等[18]以医疗设施选址为研究背景，建立了考虑个人偏好因素的整数规划模型，设计了基于拉格朗日松弛算法和次梯度松弛算法的启发式算法对模型进行求解。本文也采用拉格朗日松弛算法解决考虑时间满意度与最大覆盖率的铁路救援列车部署车站选址模型，求解过程如下：

Step 1：将难约束式(14)收敛入目标函数可得式(19)：

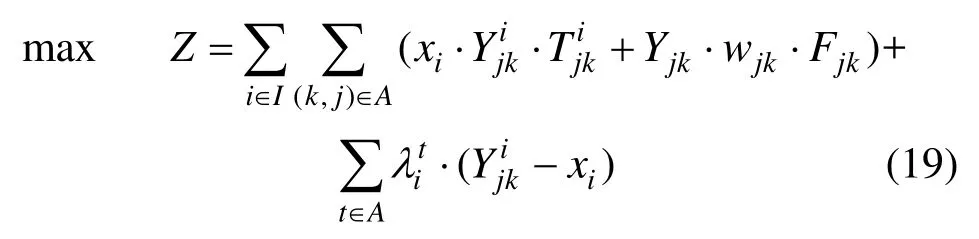
Step 2：初始化拉格朗日因子λ0=0.5；

Step 3：对 λt，从 Z(λt)中任意选取一个次梯度 st；如果st=0则λt达到最优解而停止计算；否则λt+1=max{λt+θt·st,0}，t=t+1，重复循环 Step 3。

其中，迭代乘子 θt=θ0·ρt，迭代乘数 ρ∈(0,1)。本文选取ρ=0.6。

Step 4：设置循环停止原则。1)设：ΔZ=Zt+1−Zt，当ΔZ<σ，σ为足够小的小数时(本文设σ=0.000 1)，停止循环，输出目标函数值。即目标函数在规定步数内的变化不超过0.000 1则中止计算。2) 如果 st=0则λt达到最优解而停止计算。否则重复Step 3。

3 计算实例及结果分析

时间满意函数中的系数k通过最小二乘法学习获得，文中设计专家打分的方法获得时间满意度的测试值，并对测试值取平均值数处理。经运算处理可得拟合的系数k=0.906 1≈0.9。此时拟合数据表如表2所示。

拟合数据如图5所示。

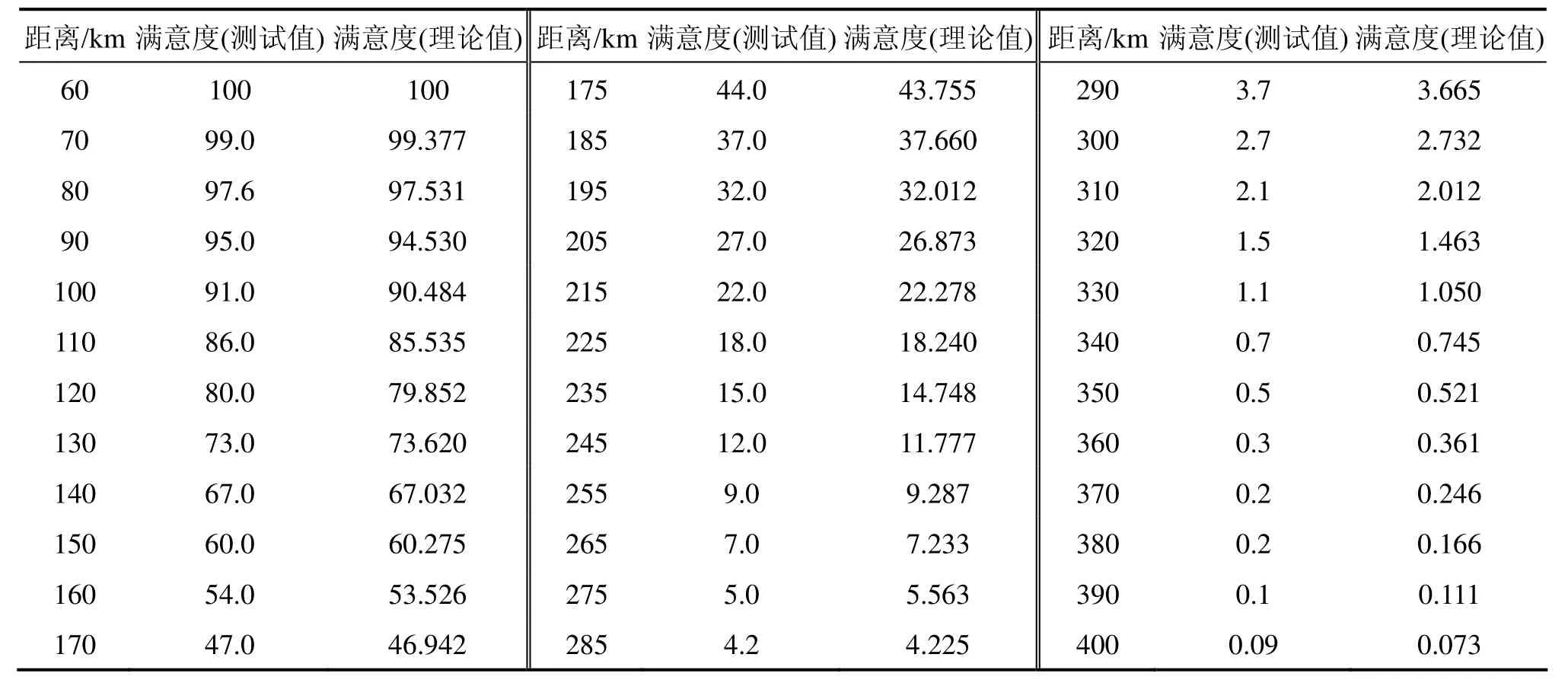
表2 时间满意函数拟合数据表Table 2 Time satisfaction function fitting the data

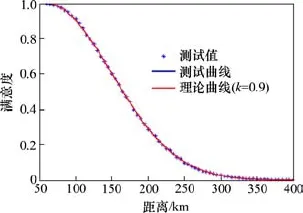
图5 时间满意系数k拟合数据图Fig. 5 Map of fitting the coefficient k in time satisfaction function

本文算例将结合中国铁路总公司兰州铁路局所属的车站及路网进行模拟计算分析，首先将兰州铁路局所属管内的车站及线路进行模型假设处理，可得如图6所示的路网示意图。

如图6(b)所示的网络G中，节点数N=20，各节点的编号对应于变量xi的编号i。其中：{x1, x3, x5,x7, x9, x10, x11, x14, x15, x16, x18, x19}∈I。根据实际的线路里程数据如表3所示。

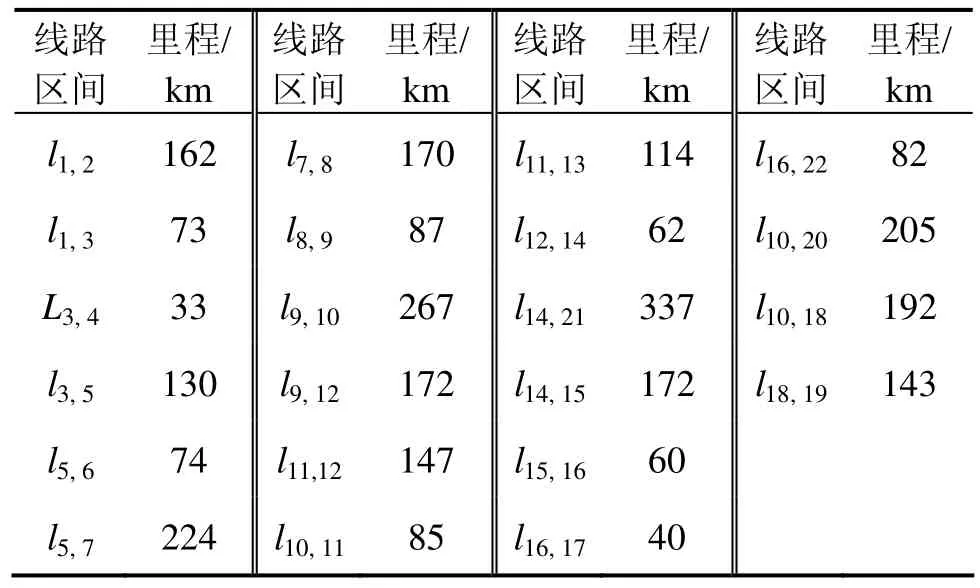
表3 兰州铁路局管内路网示意图节点间里程数据Table 3 Distance data of Lanzhou railway administration’s network

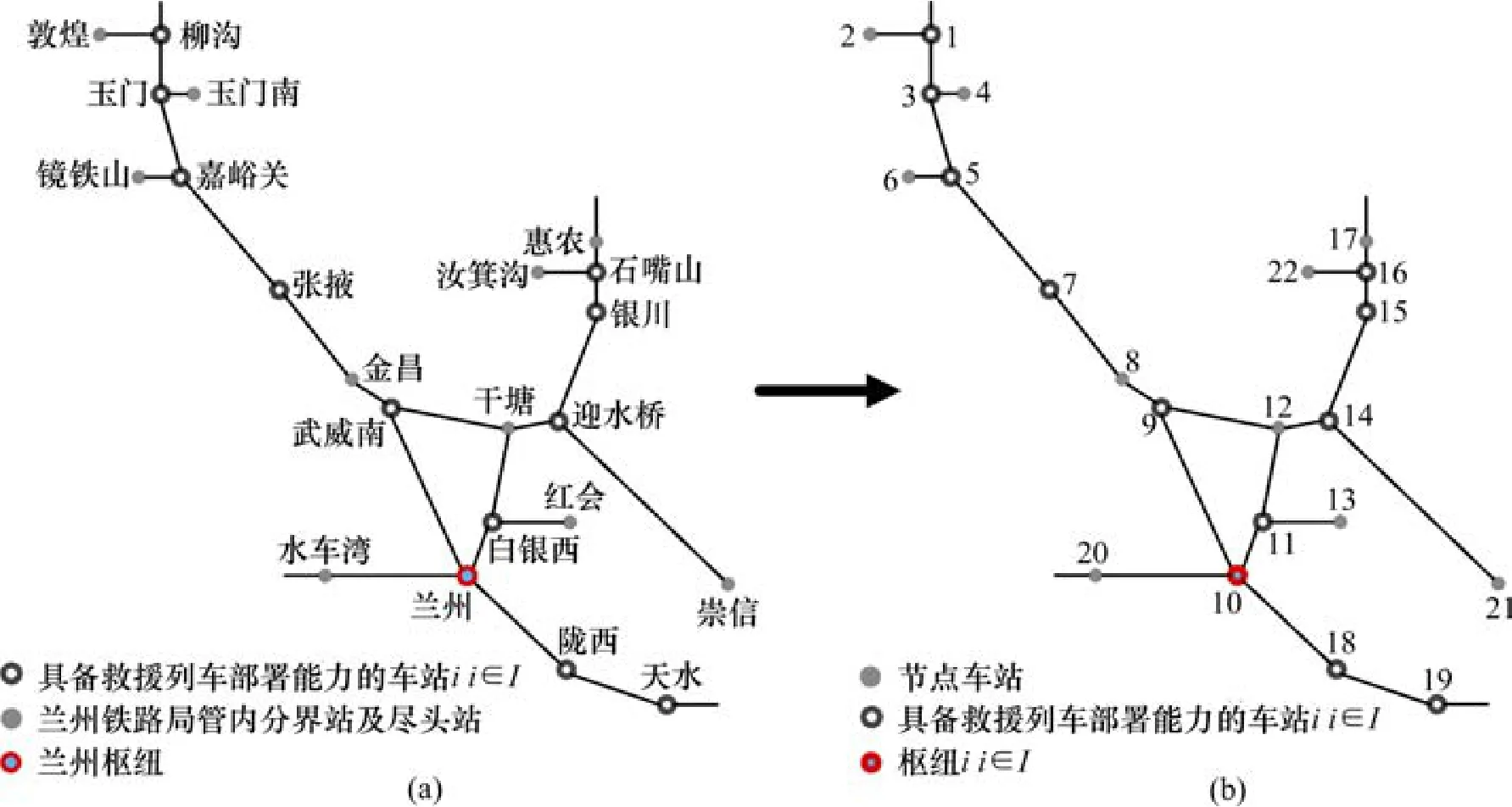
图6 兰州铁路局管内路网环境示意图Fig. 6 Simple map of Lanzhou railway administration’s network

结合本文对线路权重 wjk的定义，可得各线路区间的权重表4。

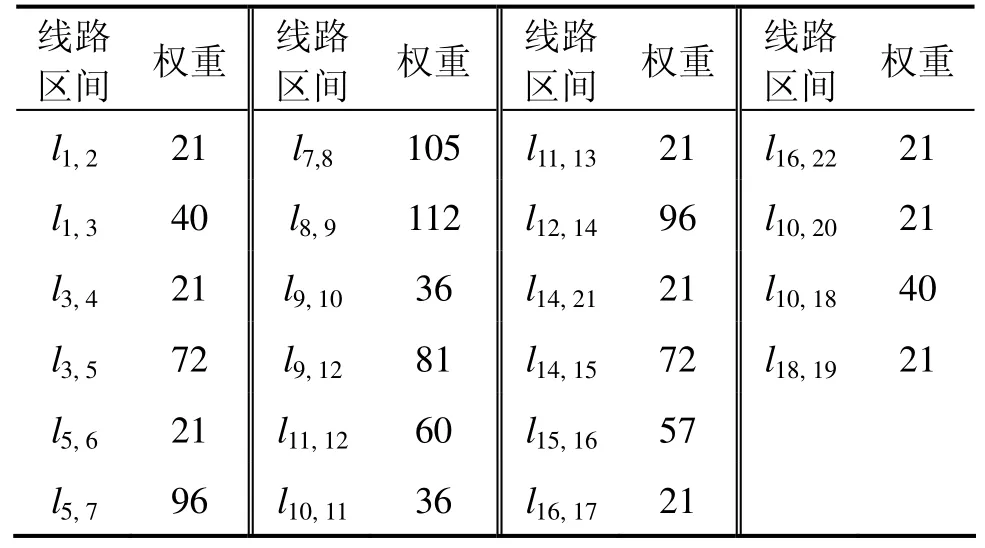
表4 兰州铁路局管内路网示意图线路权重数据Table 4 Arc weights of Lanzhou railway administration’s network

在如图6所示的路网示意图中，节点的权重如表5。

在计算的过程中为了防止局部网络导致计算结果陷入局部最优，保障对枢纽权重的维护，模型计算的过程中去要对枢纽补增权重，确保枢纽在路网中的地位。经运算可得如下结论：当p=5时计算可得，救援列车部署车站及对应的线路覆盖关系如表6所示。

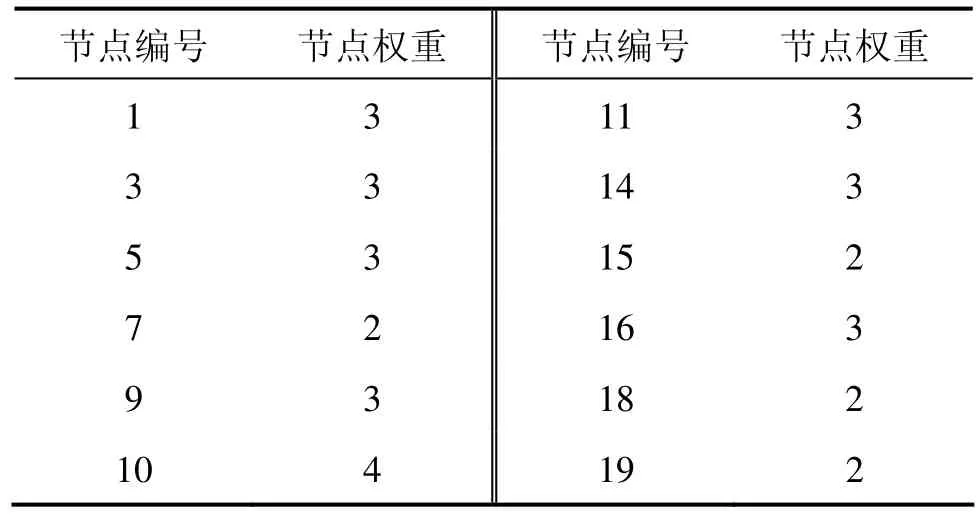
表5 兰州铁路局管内路网示意图节点权重数据Table 5 Node weights of Lanzhou railway administration’s network

表6 p=5时救援列车部署车站及覆盖关系Table 6 Locating plans for securing trains and covering relationship when p=5

当p=4时计算可得救援列车部署车站及对应的线路覆盖关系如表7所示。

表7 p=4时救援列车部署车站及覆盖关系Table 7 Locating plans for securing trains and covering relationship when p=4

当p=3时计算可得救援列车部署车站及对应的线路覆盖关系如表8所示。

表8 当p=3时救援列车部署车站及覆盖关系Table 8 Locating plans for securing trains and covering relationship when p=3

4 结论

1) 本文在最大覆盖模型的基础上，构建覆盖率函数和时间满意度函数，寻求在现有的技术条件下，决策者可以根据其实际情况和能力部署救援列车，以达到救援列车对铁路线路覆盖率最大和时间满意度最高的部署方案，在提高铁路路网鲁棒性的同时兼顾到铁路救援的时效性。本文设计的救援列车的部署模型与方法为铁路运营者在救援列车部署方案设计中提供理论依据。

2) 在对相关问题的研究中我们发现，伴随着路网结构的完善和救援技术的发展，本文中的个别数据经过抽象和假设后需要进一步完善。文章在考虑救援列车对铁路线路覆盖的同时，仅以单一铁路局为研究算例，使得计算结果具有较大的局限性。

3) 相关线路的权重仅以介数为指标的计算不够全面，没有实际考虑到线路的战略地位和线路的能力限制，以及对救援能力和覆盖结果的均衡性有待进一步研究。

[1] Hakimi S. Optimum location of switching centers in a communications network and some related graph theoretic problems[J]. Operations Research, 1965(13):462−475.

[2] Church R L, Revelle C. The maximal covering location problem[J]. Papers of Regional Science Association,1974(32): 101−118.

[3] Berman O, Krass D, Drezner Z. The gradual covering decay location problem on a network[J]. European Journal of Operational Research, 2005, 151(3): 474−480.

[4] Farahani R Z, Asgari N, Heidari N, et al. Covering problems in facility location: A review[J]. Computers &Industrial Engineering, 2012, 62(1): 368−407.

[5] Brimberg J, Schieweck R, Schöbel A. Locating a median line with partial coverage distance[J]. Journal of Global Optimization, 2015, 62(2): 371−389.

[6] WANG J, LIU H, AN S, et al. A new partial coverage locating model for cooperative fire services[J].Information Sciences, 2016(373): 527−538.

[7] Albert Y, CHEN, YU Tingyi. Network based temporary facility location for the emergency medical services considering the disaster induced demand and the transportation infrastructure in disaster response[J].Transportation Research Part B, 2016(91): 408−423.

[8] WU Yanhua, WANG Fuzhang, LI Fang. Hierarchical planning location model of railway rescue center[J].Journal of Traffic and Transportation Engineering, 2013,13(3): 86−93.

[9] Revelle C, Toregas C, Falkson L. Applications of the location set-covering problem[J]. Geographical Analysis,1976, 8(1): 65−76.

[10] Berman O, Verter V, Bahar Y. Designing emergency response networks for hazardous materials transportation[J]. Computers & Operations research, 2007(34): 1374−1388.

[11] Blanquero R, Carrizosa E, G.-tóth B. Maximal covering location problems on networks with regional demand[J].Omega, 2016(64): 77−85.

[12] CAI Wenxue, SONG Shangjiang. Arc-covering continuous decay-considered emergency allocation ofhazardous materials transportation[J]. Logistics Technology, 2010(215): 68−70.

[13] MA Yunfeng, YANG Chao, ZHANG Min, et al. Timesatisfaction-based maximal covering location problem[J].Chinese Journal of Management Science, 2006, 14(2):45−51.

[14] GUO Shize, LU Zheming. Fundamental theories on complex network[M]. Beijing: China Science Press, 2012:43−53.

[15] Dantrakul S, Likasiri C, Pongvuthithum R. Applied p-median and p-center algorithms for facility location problems[J]. Expert Systems with Applications, 2014,41(8): 3596−3604.

[16] LAI X, XU Z. Improved algorithms for joint optimization of facility locations and network connections[J].European Journal of Operational Research, 2016, 250(3):745−753.

[17] Saif A, Elhedhi S. A Lagrangian heuristic for concave cost facility location problems: the plant location and technology acquisition problem[J]. Optimization Letters,2016, 10(5): 1087−1100.

[18] Kim D G, Kim Y D. A Lagrangian heuristic algorithm for a public healthcare facility location problem[J]. Annals of Operations Research, 2013, 206(1): 221−240.