基于多目标综合评价法的边坡抗滑桩桩位优化设计

李起龙，魏红卫

(1. 中交机场勘察设计院有限公司，广东 广州 510230；2. 中南大学 土木工程学院，湖南 长沙 410075)

抗滑桩是穿过滑体，深入滑床用以平衡滑坡体下滑力的桩柱体，能够显著提高边坡的稳定性。抗滑桩通常为钢筋混凝土桩，主要承受侧向荷载作用，把滑坡推力传递到稳定土层。自20世纪60年代以来，抗滑桩作为治理滑坡的一种主要工程措施被广泛采用，取得了良好的治理效果。抗滑桩的位置对安全系数、桩身长度以及桩身内力影响很大，如何在安全性和经济性满足要求的前提下找到最合理桩位，是该领域重要的研究方向。针对这个问题，目前已有学者进行了卓有成效的研究，如：戴自航等[1]用有限元软件对抗滑桩土质边坡进行模拟后发现了不同桩长方案中桩的内力沿着桩身的分布规律和边坡安全系数随桩长改变的变化规律，认为采用强度折减法计算土坡稳定系数时，选择塑性区临界贯通为判据较为合适；年廷凯等[2]用有限元软件模拟了均质土坡中不同桩长所对应的边坡的临界滑移面的位置与形式，得到2/5桩长的合理锚固深度，最后绘出边坡临界滑移面随着桩长和桩位改变的变化规律以及边坡安全系数随桩加固位置和桩长改变的变化曲线，提出均质土坡中抗滑桩设计桩长宜为 2.5倍临界滑动面深度；张爱军[3]建立均质土坡三维有限元模型，经过对比分析后发现在优先保障安全的前提下，兼顾经济因素最合理桩位可考虑在边坡的中下部。雷文杰等[4]对滑坡治理中抗滑桩桩位的分析后发现抗滑桩位于边坡最前面时桩长短，推力小，因而是最佳的桩位。宋英杰等[5]针对抗滑桩加固后边坡稳定性评价以及桩位布设优化问题进行了深入探讨；杨光华等[6]根据滑坡产生的应力场和位移场所确定的最合理加固位置并进行了验证。李梅等[7]研究了桩位变化对抗滑桩优化设计造成的影响。王聪聪等[8]认为在抗滑桩加固边坡工程中存在一有效嵌固深度Heed，当桩长超过这一深度后继续增大桩长并不能提高边坡的安全系数。若桩长较短，则布设抗滑桩于边坡中部具有最好的加固效果；若桩长较长，则布设抗滑桩于边坡上部对边坡稳定性更有利。聂文波等[9]介绍了剩余推力法原理，深入探讨了抗滑桩设计推力的计算方法。在已有的桩位研究中，国内外学者考虑了多重因素的影响并且取得了很多有意义的成果。安全系数、滑坡推力、桩所承受的滑坡推力、桩前土体抗力以及桩长等都是影响抗滑桩桩位选取的主要因素，它们之间存在一定的矛盾性。为了得到同时满足安全性和经济性要求的桩位，本文采用多目标综合评价法对桩位选取进行优化设计，以安全系数、桩长和桩后滑坡推力作为优化目标，确定各目标权重系数，建立多目标优化模型，通过数学方法计算得到不同桩位的优属度，比较大小便可得到合理桩位，以期为边坡上合理抗滑桩桩位的选取提供理论依据。

1 优化目标值的计算

1.1 优化目标的确定原则

边坡加固设计要满足安全性和经济性的双重要求。安全性是指边坡通过抗滑桩加固后安全可靠，坡体的安全系数不小于滑坡治理设计所要求的安全系数，且不宜过大，以免造成浪费，因此，将边坡加固后的安全系数作为一个影响桩位确定的优化目标；随着桩位的改变，桩后滑坡推力也会改变，较小的水平抗力意味着较少的工程材料和工程量，明显满足经济性要求，因此，选取桩后滑坡推力作为一个影响桩位确定的优化目标；抗滑桩锚固深度设计也是比较重要的一环，决定了设计桩长，如果桩位选择不当，临界滑动面过深导致设计桩长较大，不仅施工难度大、浪费材料，而且桩身可能由于桩顶横向变形过大而导致桩身局部开裂，造成严重的安全隐患，故将设计桩长作为一个影响桩位选择的优化目标。

本文选择安全系数，桩身长度，桩后滑坡推力作为桩位选择的3个优化目标。

1.2 计算方法的确定

为了更加准确、合理的计算各个目标值的大小，宜结合工程实践经验并采用不同种方法对比分析。目前用于边坡抗滑桩设计的计算方法主要有 2种：传统极限平衡法与数值分析法。传统极限平衡法以Mohr-Coulomb强度理论为基础，通过分析土体在破坏那一刻的静力平衡来求得问题的解，本文拟采用已经广泛被应用于计算滑坡推力的传递系数法。数值分析法是根据运动学及弹塑性力学基本原理，借助边坡内任意一点处的平衡微分方程、几何方程、物理方程以及运动学方程来求解边坡任意一点处的应力、应变状态，该方法从一定程度上较好的解决了地质体的三维问题及边界条件，相比传统极限平衡法具有一定的优点，为此本文将采用ABAQUS有限元软件进行数值分析。

1.3 边坡的选取及数值模型的建立

为了可以和已有研究成果进行对比，引用文献[2]中的经典边坡算例。抗滑桩为钢筋混凝土桩，线弹性材料，桩的截面为矩形，宽b=1 m，高h=1.5 m，桩间距为 4 m。边坡土体采用服从 Mohr-Coulomb破坏准则的理想弹塑性模型，桩−土间的相互作用模式是法向接触，摩擦系数为 0.4，桩头自由。以坡脚点突变位移作为边坡失稳判据。初始应力场按自重应力场考虑，所有模型采用统一的边界条件，即边坡两侧边Z方向水平位移约束，底边X，Y和Z方向全约束。利用有限元软件得到边坡失稳时的坡体内部塑性贯通区域，此区域即可看作初始潜在滑移面。此边坡在没有支挡结构的情况下，用数值分析法算得稳定系数为 1.14，与 Won等[11−12]所得的稳定系数 1.13～1.20基本一致，比较合理，微小的差别可能源于网格划分、数值算法、失稳依据等因素。土体有关的参数见表 1，有限元模型如图 1所示。

1.4 桩后滑坡推力的计算

工程设计中往往用该处的滑坡推力作为设计桩后滑坡推力，而实际上，用抗滑桩加固后的边坡，由于桩−土相互作用的存在，坡体内部会发生应力重分布。为了验证用数值分析法计算得到的桩后滑坡推力是否合理，本文先采用剩余推力法计算不同桩位处的滑坡推力F1，再用有限元强度折减法计算桩后土推力F2与桩前土体抗力F3。

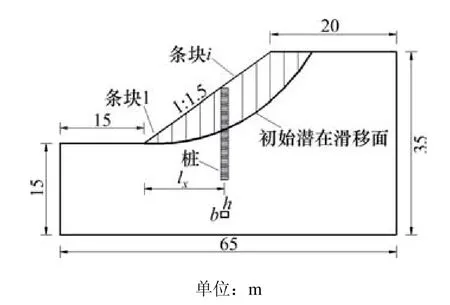
图1 边坡尺寸Fig. 1 Size of slope

表1 抗滑桩和土体的物理力学参数Table 1 Physico-mechanical parameters of piles and soil

计算土坡条块简图如图1所示，将桩分别设置在土块分界处。lx是桩位距坡脚的水平距离，不断改变抗滑桩在坡体中的位置，使lx从3 m变化到33 m，同时选取4 m宽的土体作为计算宽度。通过有限元软件的后处理模块中提供的路径分析功能，将土体对桩身的水平应力沿着桩身映射到从滑面到桩顶的路径上。

抗滑桩设置于边坡lx=21 m，12 m处桩身水平应力大小及分布如图2～3所示，利用积分公式沿此路径对水平应力进行积分便得到桩后土推力与桩前土体抗力。

1.5 桩长度的确定

根据文献[1]和[2]中的关于桩长的研究结论及相应模拟后发现，当桩长小于2倍初始临界滑动面深度时，新的滑移面总是通过桩底，从而导致抗滑桩无法形成嵌固作用，加固效果不好，如图4所示。故取 2.5倍初始临界滑移面深度作为桩身计算长度。

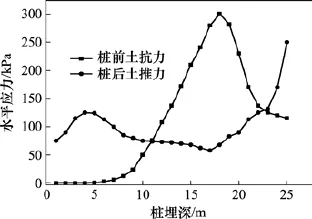
图2 lx=21 m时桩所受土压力分布Fig. 2 Distribution of soil pressure on piles when lx=21 m

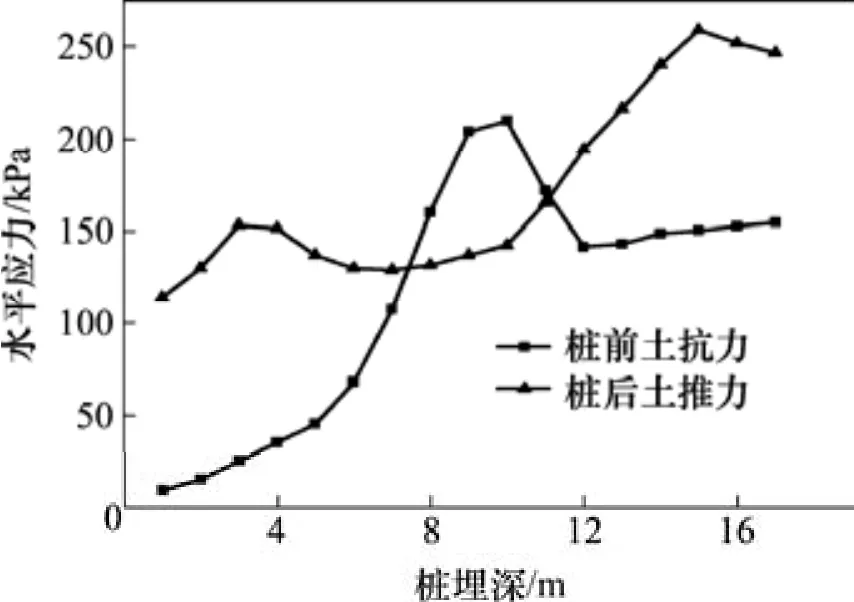
图3 lx=12 m时桩所受土压力分布Fig. 3 Distribution of soil pressure on piles when lx=12 m

图4 不同桩长l对应的临界滑移面深度Fig. 4 Different length of the pile corresponding to the depth of the slip surface

1.6 边坡安全系数的计算

抗滑桩−边坡体系加固后安全系数可以采用数值分析法中强度折减理论进行计算。强度折减法的实质就是将材料的黏聚力和内摩擦角按照一个设定的系数逐渐减小，从而导致某单元的应力超过了屈服面，不能承受的应力将逐步转移到周围土体单元中，当出现连续滑动面即滑移面塑性贯通之后，土体将失稳，而这个折减系数大小就可以看作是边坡的安全系数，它随桩位的变化如图5所示。

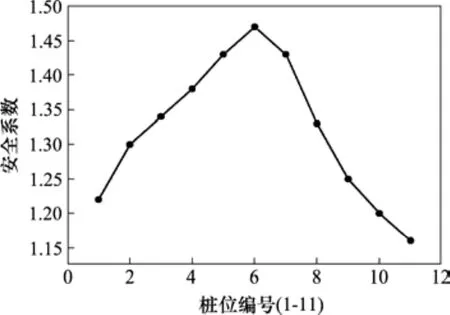
图5 安全系数分布Fig. 5 Distribution of the safety factor

1.7 计算结果分析

将用数值分析法计算得到的桩后土推力 F2与采用传递系数法计算得到的滑坡推力 F1进行对比后发现两者相差不超过10%，这说明数值分析法计算滑坡推力是可行的，与文献[3]的结论一致。

随着在边坡上桩位的不同，滑移面也会发生相应的改变，数值分析软件可以很好地模拟这一过程。如图6所示，当桩位在边坡中下部时，滑移面剪出口出现在桩顶附近，并且随着桩位沿边坡的上移而上移，整个滑移面是一个近似的圆弧；当桩位选择在边坡上部，lx=21 m时，边坡滑移面的变化趋势发生了突变，剪出口不再出现在桩顶，而是坡脚处，整个滑移面也不再近似为圆弧形，桩前土体与抗滑桩发生了分离，如图8所示。

从表2可见，用数值分析法还得到了桩前土体抗力F3的大小，这个力是客观存在的，不能忽略。由于桩身发生弯曲后挤压桩前的土体，导致土体发生一定的塑性变形，对抗滑桩产生反作用力，这就是桩前土抗力。如图7所示，它的大小近似等于桩后土推力与桩后滑坡推力之差，呈现抛物线形式，峰值出现在边坡中部，边坡底端和边坡上部比较小，这是由于抗滑桩设在边坡底端时，桩前土产生的塑性变形较小，所提供的抗力基本可以忽略；桩位选在边坡中部时，桩前土体产生了较大的塑性变形，也就提供了相当可观的抗力；当桩位选在边坡上部时，桩前土体由于没有有效的支护处于欠稳定的状态，内部发生滑动形成了新的局部贯通破坏滑动面，此时桩与土发生了分离，桩前土不能提供足够的抗力，如图9所示。

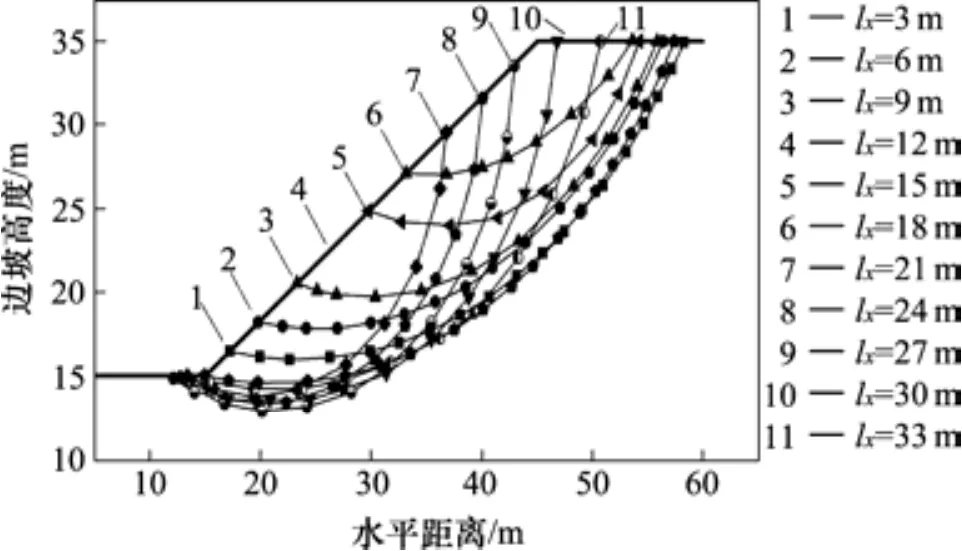
图6 滑移面随桩位不同所发生的改变Fig. 6 Slip surface varies with the pile location

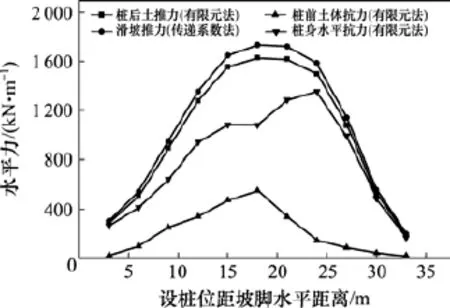
图7 计算结果Fig. 7 Calculation results

图8 lx=21 m时滑移面云图Fig. 8 Nephograms of the slip surface when lx=21 m

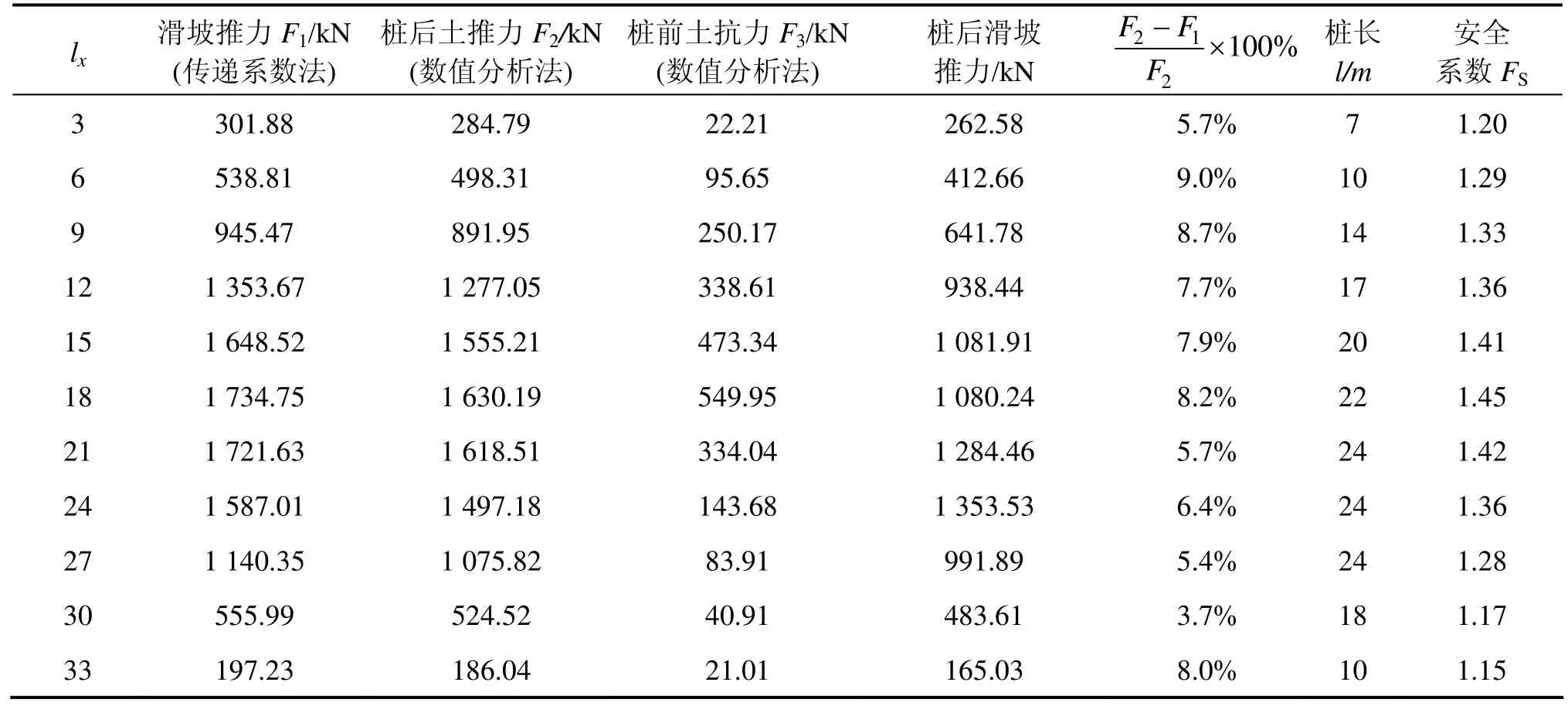
表2 不同桩位处的计算结果Table 2 Calculation results of different piles

由于桩前土体抗力的改变，桩后滑坡推力曲线在中间出现一个明显的平台，极值出现在平台边缘，这说明中部设桩时加固效果很好，可以很好的利用边坡的自稳性。但是在此处的抗滑桩的长度长，施工难度较大，施工过程中可能出现新的临空面，甚至诱发滑坡。

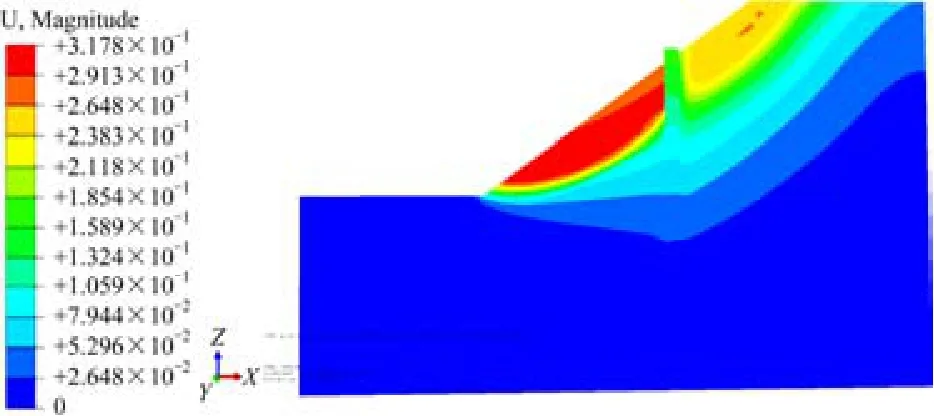
图9 lx=21 m时边坡位移云图Fig. 9 Nephograms of level displacement when lx=21m

综上所述，数值分析法的优点在于充分考虑了桩−土间相互作用以及土体的塑性变形，用此方法得到桩后滑坡推力大小与滑面处桩所受到的剪力相近，符合一般的力学规律。由于传递系数法的前提及假设条件所具有的局限性，未考虑滑块间的塑性变形所产生的土体抗力，这样一来算得的滑坡推力必然会比实际情况偏大，导致在抗滑桩设计的过程中偏于保守，使得抗滑桩设计桩身内力估值偏大，本文采用数值分析法计算的结果进行桩位优化设计研究。

2 抗滑桩桩位的优化设计

2.1 方法可行性研究

多目标综合评价法把研究对象作为一个系统，按照分解、比较判断、综合的思维方式进行决策，成为继机理分析、统计分析之后发展起来的系统分析的重要工具。系统的思想在于不割断各个因素对结果的影响，而多目标综合评价法中权重设置最后都会直接或间接影响到结果，而且在层次中的每个因素对结果的影响程度都是量化的，非常清晰和明确。这种方法尤其可用于对无结构特性的系统评价以及多目标、多准则等的系统评价。

综上所述，影响桩位选择的3个因素：桩后滑坡推力、桩长以及安全系数对最后的结果有很大的影响，利用多目标综合评价法将它们之间的关系进行量化，通过简单的数学计算就可以找到最合理桩位。

2.2 评价指标归一化处理

为了使各组数据有可比性，需要对其进行归一化处理。常用的归一化方法有最大−最小标准化方法，是对原始数据进行线性变换，将目标函数组任意一个原始值 α通过最大−最小标准化映射到区间[0,1]上S，S就是目标值的相对优属度。

对于越大越优的公式如下：

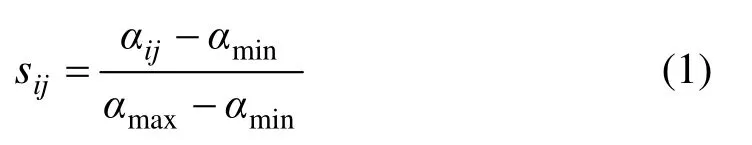
式中：αij为第j方案的目标i的目标值，αmax和αmin分别为相应目标所能取的最大与最小值。上文中只有安全系数属于越大越优的目标，其最大值可取为1.5。

对于越小越优的公式如下：

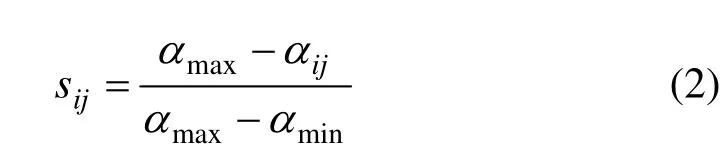
本文算例中桩长和桩后滑坡推力属于越小越优的目标，可根据实际值选择相对应的目标值。

2.3 多目标综合判断

把上述得到的不同方案目标值的相对优属度值进行综合，确定不同种抗滑桩加固方案的优属度kj，其计算方法如下：

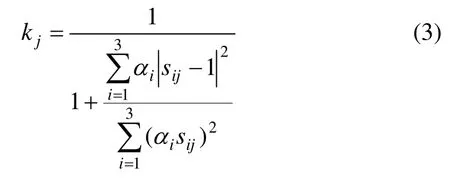
kj值的大小决定了方案的优属度，αi为目标的权重值满足：

2.4 各目标权重系数的确定

通常定性区分事物的能力习惯用5个属性来表示，即同样重要、稍微重要、较强重要、强烈重要、绝对重要，可以取2个相邻属性之间的值，这样就得到9个数，即9个标度。为了便于将比较判断定量化，引入 1-9比率标度法，规定用 1，3，5，7和9分别表示根据经验判断，要素i与要素j相比：同样重要、稍微重要、较强重要、强烈重要、绝对重要，而 2，4，6和 8表示上述两判断之间的折中值。

本文中有桩后滑坡推力Q1，桩长Q2，安全系数Q3等3个目标值，结合决策者的意向、工程经验和专家判断等，得出各目标的相对权重赋值见表4。

表3 标度取值Table 3 Value of scale

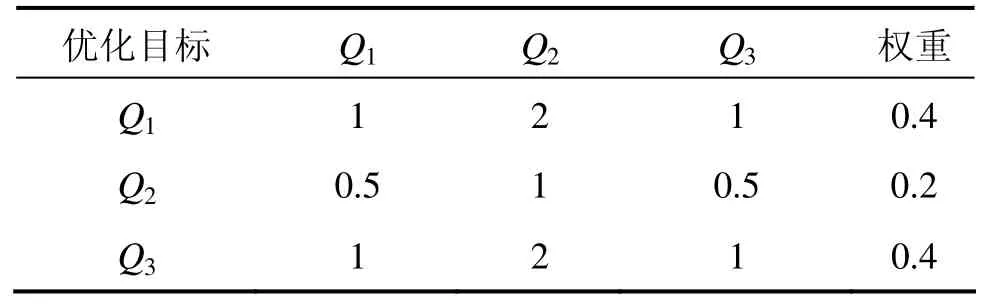
表4 各目标相对权重赋值Table 4 Weight assignment for every target

将上述3个元素参与比较，构造成对比较矩阵

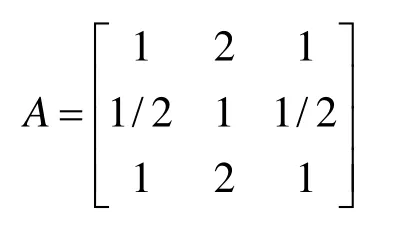
根据层次法原理，利用 A的理论最大特征值λmax与n之差检验一致性。一致性指标：

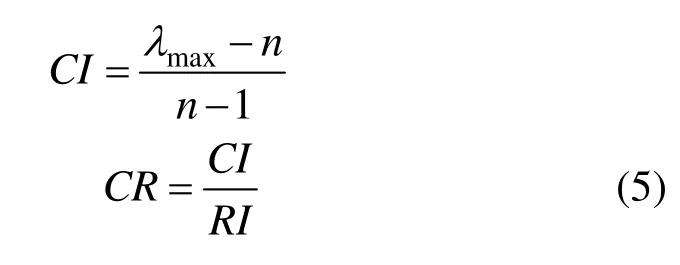
式中：RI为平均随机一致性指标，可直接查得，对于3阶矩阵，RI=0.58。一般认为CI<0.1, CR<0.1时，判断矩阵的一致性可以接受，否则重新两两进行比较。

通过计算分析，λmax=3, CI=0, RI=0.58, CR=0 3个目标的排序具有满意一致性。

3 算例结果

基于上文数值分析法所得到的抗滑桩-边坡体系中不同桩位处桩后滑坡推力、桩身长度和安全系数的计算结果，采用上述桩位的优化分析方法进行计算，结果见表5。

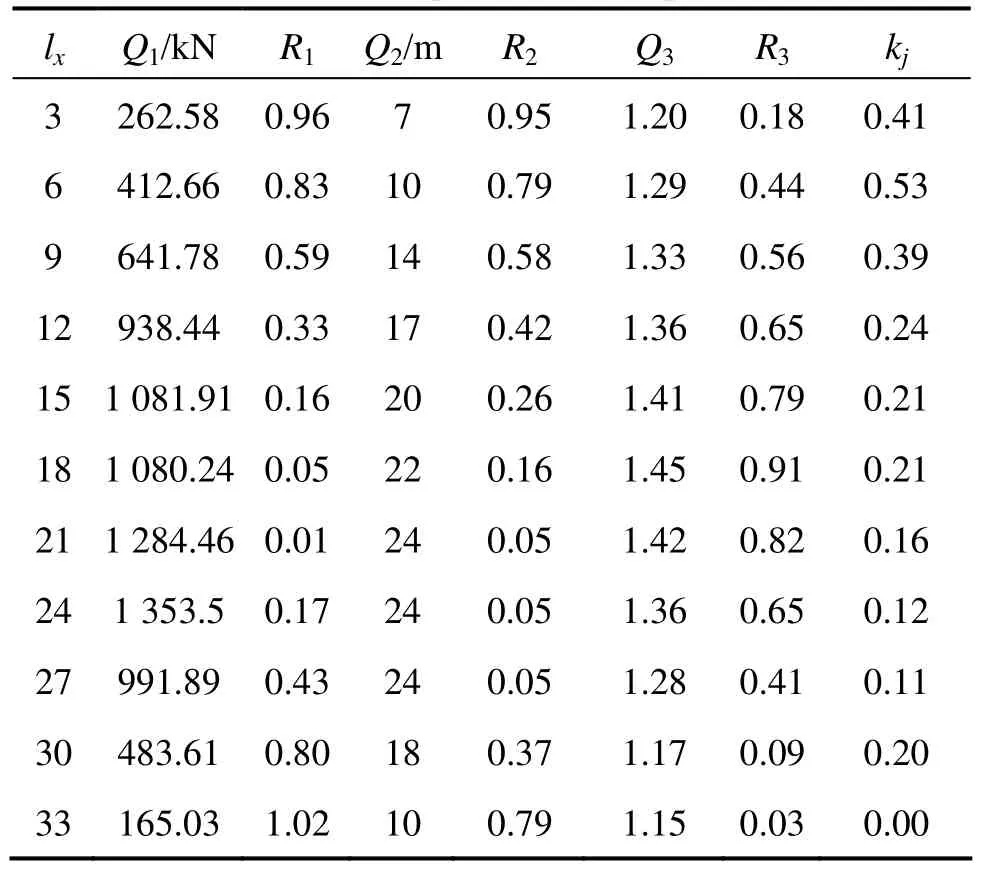
表5 桩位选择优化分析Table 5 Optimization for piles

根据最优判定原则，lx=6 m所对应的评价指标kj=0.53是最大的，所以距坡脚水平距离为6 m处的桩位是最合理的选择，这与一般实际工程中将桩位设置在边坡中下部一致。

4 结论

1) 将用数值分析法和传递系数法所计算的滑坡推力进行比较后发现两者相差不超过10%，说明数值分析法计算桩后滑坡推力是可行的。

2) 随着桩长的增加，滑移面向边坡内部发展，当桩长达到一定长度后，滑移面发生突变，变为浅层滑动，剪出口出现在桩顶；整个边坡上桩前土体抗力呈现抛物线形式，边坡中部数值最大，到了中上部位置急剧减小，这与工程实际情况一致；桩后滑坡推力曲线在边坡中部明显出现一个平台，主要是由于此处设桩能最大程度发挥桩前土抗力。

3) 将多目标综合评价方法应用于桩位优化设计中所得的结果与已有的将桩位设在边坡中下部较为合理的研究结论相符，说明该方法能够用于桩位的优化设计。其他类型复杂边坡可以参照本文算例的计算过程，建立相应优化模型进行分析。

[1] 戴自航, 徐祥. 边坡抗滑桩设计计算的三维数值分析法[J]. 岩石力学与工程学报, 2012, 31(12): 2572−2578.DAI Zihang, XU Xiang. 3D finite element method for design computations of anti-slide piles[J]. Chinese Journal of Rock Mechanics and Engineering, 2012,31(12): 2572−2578.

[2] 年廷凯, 徐海洋, 刘红帅. 抗滑桩加固边坡三维数值模拟中的几个问题[J]. 岩土力学, 2012, 33(8): 2522−2535.NIAN Tingkai, XU Haiyang, LIU Hongshuai. Several issues in the three-dimensional numerical analysis of slopes reinforced with anti-slide piles[J]. Rocks and Soil Mechanics, 2012, 33(8): 2522−2535.

[3] 张爱军. 挡土桩—土相互作用模型及抗滑桩加固边坡简化计算方法研究[D]. 广州: 华南理工大学, 2013.ZHANG Aijun. Model of interaction between pile and soil & simplified calculating method of pile used to stability unstable slope[D]. Guanghzou: South China University of Technology, 2013.

[4] 雷文杰, 郑颖人, 冯夏庭. 滑坡治理中抗滑桩桩位分析[J]. 岩土力学, 2006, 27(6): 950−954.LEI Wenjie, ZHENG Yingren, FENG Xiating. Analysis of pile location on landslide control[J]. Rocks and Soil Mechanics, 2006, 27(6): 950−954.

[5] 宋英杰, 陈文强, 李长冬. 抗滑桩加固后边坡稳定性评价与桩位优化研究进展[J]. 安全与环境工程, 2016,23(5): 43−49.SONG Yingjie, CHEN Wenqiang, LI Changdong.Research progress of the stability evaluation of slope reinforced with stabilizing piles and optimization of pile location[J]. Safety and Environmental Engineering, 2016,23(5): 43−49.

[6] 杨光华, 钟志辉, 张玉成. 根据应力场和位移场判断滑坡的破坏类型及最合理加固位置确定[J]. 岩石力学与工程学报, 2012, 31(9): 1879−1887.YANG Guanghua, ZHONG Zhihui, ZHANG Yucheng.Identification of landslide type and determination of optimal reinforcement site based on stress field and displacement filed[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(9): 1879−1887.

[7] 李梅, 刘校, 邹蓓, 等. 桩位变化对抗滑桩设计优化的研究[J]. 武汉理工大学学报, 2013, 35(11): 94−97.LI Mei, LIU Xiao, ZOU Bei, et al. Study on pile location change to optimization of anti-side pile design[J]. Journal of Wuhan University of Tecchnology, 2013, 35(11): 94−97.

[8] 王聪聪, 李江腾, 廖埈, 等. 抗滑桩加固边坡稳定性分析及其优化[J].中南大学学报(自然科学版), 2015, 46(1):231−237.WANG Congcong, LI Jiangteng, LIAO Jun, et al.Stability analysis of slope reinforced with piles and optimization[J]. Journal of Central South University(Science and Technology), 2015, 46(1): 231−237.

[9] 聂文波, 张利洁, 胡江运. 滑坡治理中抗滑桩设计推力计算探讨[J]. 岩石力学与工程学报, 2004(增2): 5050−5052.NIE Wenbo, ZHANG Lijie, HU Jiangyun. Study on designed thrust of anti-slide pile[J]. Chinese Journal of Rack Mechanics and Engineering, 2004(Suppl 2): 5050−5052.

[10] LI X, PEI X, Gutierrez M, et al. Optimal location of piles in slope stabilization by limit analysis[J]. Acta Geotechnica, 2012, 7(3): 253−259.

[11] Won Jinoh, You Kwangho, Jeong Sangseom, et al.Coupled effects in stability analysis of pile-slope systems[J]. Computers and Geotechnics, 2005, 32(4): 304−315.

[12] WEI W B, CHENG Y M. Strength reduction analysis for slope reinforced with one row of piles[J]. Computers and Geotechnics, 2009, 36(7): 1176−1185.

[13] 咸玉建, 陈学军, 汪志刚, 等. 基于有限元强度折减系数法岩土边坡稳定性分析与抗滑桩设计[J]. 地质科技学报, 2015, 34(4): 176−182.XIAN Yujian, CHEN Xuejun, WANG Zhigang, et al.Stability analysis of rock slope and anti slide pile design based on finite element strength reduction coefficient method[J]. Geological Science and Technology Information, 2015, 34(4): 176−182.

[14] 唐芬, 郑颖人, 杨波. 双排抗滑桩的推力分担及优化设计[J]. 岩石力学与工程学报, 2010, 29(增1): 3162−3168.TANG Fen, ZHENG Yingren, YANG Bo. Thrust share ratios and optimization design for two-row anti-slide piles[J]. Chinese Journal of Rock Mechanics and Engineering,2010, 29(Suppl 1): 3162−3168.

[15] LUAN M T, WU Y T, Nian T K. An alternating criterion based on development of plastic zone for evaluating slope stability by shear strength reduction FEM[C]//Proceedings of the Sina-Japanese Symposium on Geotechnical Engineering-Geotechnical Engineering in Urban Construction. Beijing: Tsinghua University Press,2003: 181−188.