板式轨道充填层自密实混凝土的动态力学特性

龙广成，李宁，谢友均，马昆林

(中南大学 高速铁路建造技术国家工程实验室，湖南 长沙 410075)

CRTS III型板式无砟轨道是具有我国自主知识产权的高速铁路无砟轨道结构型式，其显著特点之一是充填层采用自密实混凝土(Self-compacting Concrete，简写为SCC)。板式无砟轨道常处于动荷载服役条件，而目前对充填层SCC在动荷载下的性能研究相对较少。研究表明，混凝土材料在动荷载作用下表现出与静态加载明显不同的规律[1]。Dilger等[2−3]发现混凝土的抗压强度随应变率的增大而线性增加，而 Suaris[4]则认为混凝土抗压强度的增长与应变率呈非线性关系。Yousef等[5]研究表明混凝土动态强度增长因子(DIF)随应变率先线性增大后急剧增大。充填层SCC在浇注成型工艺和组成上均有别于普通混凝土，如SCC中常含有较多的浆体、较少的粗骨料和总骨料体积。上述组成与成型工艺特点，会影响SCC内部微结构，进而影响其宏观性能[6−7]。充填层是轨道结构的关键结构部件，其破坏失效会造成轨道结构服役性能与状态发生改变，甚至危害高速铁路运营安全[8−9]。因此，深入研究充填层 SCC在动荷载作用下的力学行为对于掌握CRTS III型板式无砟轨道在高速列车动载作用条件下的服役行为具有重要意义。鉴于此，本文采用直径为75 mm的分离式霍普金森压杆(Split Hopkinson Pressure Bar，SHPB)试验装置，研究充填层SCC在不同应变率下的力学特性，以深入理解充填层SCC的动态力学行为。

1 试验概况

1.1 试验原材料、配合比及试件制备

充填层自密实混凝土(SCC)采用的原材料包括水泥、粉煤灰、矿渣、粗细集料、黏度改性材料、高效减水剂等。P.O 42.5普通硅酸盐水泥(C)由湖南东坪水泥有限公司生产，Ⅰ级粉煤灰(FA)和矿渣粉(GGBS)分别由湖南湘潭电厂和上海宝钢新材料公司提供，水泥、粉煤灰及矿渣的物理化学性能如表1所示。

表1 水泥、粉煤灰和矿渣的物理化学性能Table 1 Physical and chemical properties of C, FA and GGBS %

黏度改性剂、减水剂等由安徽中铁材料公司提供，其中羧酸系减水剂(SP)减水率为26%。细集料采用普通河砂，为符合级配要求的中砂，其细度模数为2.7，表观密度为2 650 kg/m3；粗集料采用石灰石质碎石，表观密度为2 680 kg/m3，试验中选用5～10 mm和10～16 mm 2种级配混配而成；拌合水为饮用自来水。试验各原材料性能均满足《高速铁路 CRTSⅢ型板式无砟轨道自密实混凝土暂行技术条件》(TJ/GW 112—2013)的相关规定。

试验时，先将各固体原材料倒入混凝土强制式搅拌机中拌合15 s左右，然后将减水剂和水的混合液缓慢加入搅拌机中，并继续搅拌2.5 min，搅拌速度50 r/min，试验环境温度约为22～25 ℃。拌合物性能测试完成后，立即将拌合物充入试模，试件成型24 h后拆模并放入标准养护室中养护至56 d进行动态力学试验。所得充填层SCC拌合物性能测试结果如表2所示。测得SCC 56 d静态抗压强度为48.8 MPa，弹性模量为36.6 GPa。

试件测试前用自动磨平机将试件上下底面磨平，平行误差不超过0.02 mm，磨平后的试件如图1所示。

图1 用于SHPB试验的SCC试件Fig. 1 SCC specimens for SHPB test

1.2 试验方法

试验采用Ф75 mm的SHPB试验测试系统，该系统主要由发射腔、冲头(子弹)、入射杆、透射杆、吸收杆和数据采集系统组成，如图2所示。

表2 SCC拌合物性能Table 2 Properties of fresh SCC

图2 SHPB试验装置图Fig. 2 Test system of SHPB

测试系统采用CS-10型超动态应变仪，具有校准和自动平衡功能；采用半周期正弦波加载，延长了入射波上升沿的升时，可保证试件内的应力均匀[10]。通过测试系统获得的入射应变εI(t)，反射应变εR(t)及透射应变εT(t)可计算出混凝土试件的应力σ(t)，应变 ε(t)及应变率 θ(t)[11]：

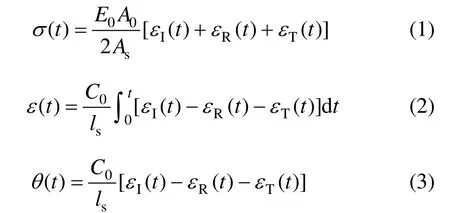
式中：A0和 E0分别为杆的横截面积和弹性模量；As和ls分别为试件的横截面积和长度；C0为压杆中纵波波速。

2 试验结果及分析

2.1 试件破坏形态

充填层 SCC试件在不同应变率下的破坏形态如图3所示。由图3可知，SCC试件的破坏形态具有明显的应变率效应。在静荷载下，试件为剪切破坏，破坏时有一条贯通的主裂缝(图 3(a))。当应变率为23.17 s−1时，SCC破坏形态与静态条件下类似，有数条贯通主裂缝形成(图 3(b))。当应变率增至34.02 s−1时，SCC破坏形态发生了明显变化：试件破坏时不再完整，而是破碎为较大的几块(图3(c))。随应变率的增大，试件的碎块尺寸显著减小，碎块数量明显增多(图3(d)～3(f))。

图3 充填层SCC试件在不同应变率下的破坏照片Fig. 3 Failure mode pictures of SCC specimens under different strain rates

不同应变率下 SCC破坏形态与加载过程中试件内部损伤演化和能量吸收密切相关。SCC作为多相复合材料，其内部存在较多的初始微裂纹和微孔洞等缺陷，其中以粗集料和水泥石的界面过渡区最为薄弱。在静荷载下，界面在某一取向上的微裂纹首先发展汇合形成主裂缝[12]。主裂缝的发展使周围的应力得到松弛，抑制了其他小裂纹的产生和发展；主裂缝在充足的时间内沿界面过渡区扩展、贯通，直至试件破坏为两块或数块。随应变率增大，荷载作用时间缩短，微裂纹来不及扩展形成主裂缝。同时由于裂纹产生所需的能量远比其扩展所需的能量高，因此需要产生更多的微裂纹来吸收巨大的冲击能量[13]。最终试件内大量微裂纹多点同时起裂，导致碎块尺寸减小，碎块数量增多。随应变率的增大，SCC内部裂损演化过程如图4所示。

图4 动荷载作用下充填层SCC内部裂损变化示意图Fig. 4 Damage evolution of filling layer SCC under dynamic load

2.2 峰值强度

图5给出了充填层SCC试件在不同应变率下的应力−应变关系曲线，其中圆柱体试件在准静态条件下的平均抗压强度为53.6 MPa。

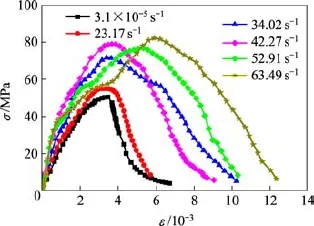
图5 不同应变率下充填层SCC的应力−应变关系Fig. 5 Stress-strain relationship of filling layer SCC under different strain rates

由图5可知，SCC的峰值强度整体上随应变率的增大而增大，但增加速率逐渐减小。当应变率从23.17 s−1增加至 42.72 s−1时，峰值强度增大了39.4%，而应变率从 42.72 s−1增加至 63.49 s−1时，峰值强度仅增大了9.8%。这是因为在高应变率下，SCC试件内部的微裂纹未能及时开裂贯通，出现变形滞后现象，根据冲量定理或功能原理，应力增大以抵消冲击能量，导致试件的峰值应力随应变率的增大而提高。另一方面随着 SCC应变率的提高，SCC试件中心部位的侧向变形由于惯性作用而受到约束，处于近似围压状态，应变率越高，其约束作用越大，这时材料的破坏应力就越高[14]。然而，试件约束侧向变形的惯性作用会随着扩展裂纹数量的增多而被削弱，因此峰值强度的增加速率逐渐减小。

为更好描述 SCC动态峰值强度随应变率的变化程度，引入动态强度增长因子(σd/σs)做进一步分析，其中σd和σs分别表示SCC的动态和准静态峰值强度。为便于比较分析，作者从公开发表的文献中归纳了相似试验条件下的普通混凝土的动态强度增长因子结果[5,13,15−17]，如图6所示。

由图6可知，对于强度介于40～120 MPa之间的混凝土而言，随着应变率的增加，动态强度增长

因子逐渐增大，混凝土的动态强度增长因子随应变率的变化规律与混凝土强度等级没有明显的相关性，这与文献[18−19]的研究结果一致。与普通混凝土相比，本文测试得到的相同应变率条件下的SCC的动态强度增长因子更大些，即在相同应变率条件下，SCC的强度增长高于普通混凝土。这一结果与SCC的组成和成型工艺特点密切相关。SCC中浆体含量较高，其“自密实”成型也避免了因机械振捣力产生的局部液化作用造成的薄弱界面区，使得硬化后的SCC与普通混凝土相比，其内部缺陷更少，结构更为致密，薄弱的界面过渡区得到明显改善。因此，在高应变率下，SCC试件内部缺陷更难扩展贯通，巨大的冲击能量更不易被吸收，因此只能通过增加更多的应力来抵消。为进一步科学表征SCC动态强度随应变率的变化规律，对上述所测SCC的试验数据进行了归一化处理，得到了SCC试件动态强度增长因子随应变率比值(θd/θs)的变化规律，如图7所示，其中θd和θs分别表示试件的动态和准静态应变率。

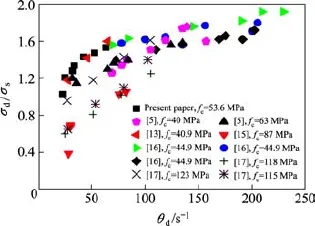
图6 自密实混凝土(本文结果)与普通混凝土[5, 13, 15−17]动态强度应变率效应比较Fig. 6 Strain-rate effect comparison of SCC (present paper)and normal concrete[5, 13, 15−17]

由图7可以看出，SCC的动态强度增长因子随应变率比值的对数增大而线性增大，其拟合公式为式(4)，其中 R2=0.9283，R为拟合结果与试验结果的相关系数。

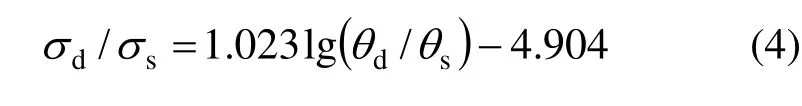
由式(4)可知，SCC的动态强度增长因子随应变率的增长系数为1.023，大于文献[20]得到的相似强度等级的普通混凝土的动态峰值强度随应变率的增长系数 0.562，进一步说明了自密实混凝土抗压强度具有更大的应变率敏感性。

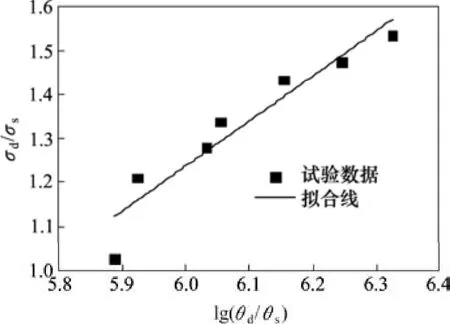
图7 SCC的动态强度增长因子与应变率比值对数的关系Fig. 7 Relationship between dynamic strength increase factor of SCC and logarithm of strain-rate ratio

2.3 峰值应变

由图5可知，SCC的峰值应变呈现出与峰值强度相似的变化规律，即其峰值应变随应变率的增大而增大，但增大速率逐渐减小。当应变率从23.17 s−1增加至42.72 s−1时，峰值应变增大了42.4%。而应变率从42.72 s−1增加至63.49 s−1时，峰值应变增大了27.3%，增加速率明显减小。采用与2.2节类似的数据处理方法来分析 SCC峰值应变与应变率的关系，得到峰值应变增长因子(εd/εs)与应变率比值的关系，如图8所示，其中εd和εs分别表示试件的动态和准静态峰值应变，εs=2 000 μ。

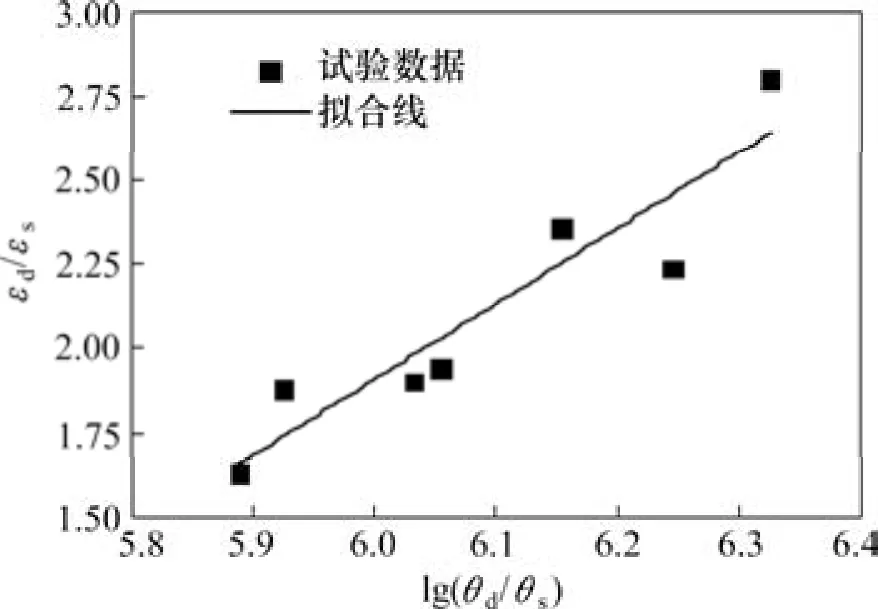
图8 SCC动态应变增长因子与应变率比值的对数关系Fig. 8 Relationship between dynamic strain increase factor of SCC and logarithm of strain-rate ratio

由图8可以看出，SCC峰值应变比值随应变率比值的对数增大而线性增大，其拟合公式为式(5)，其中R2=0.905 8。

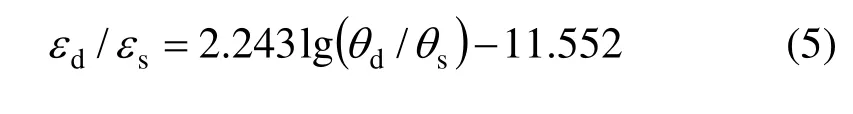
对比式(4)和(5)可以看出，在应变率变化相同时，动态应变增长因子随应变率的变化大于动态强度增长因子，表明SCC的峰值应变的应变率敏感性高于峰值强度。

2.4 弹性模量

弹性模量是描述混凝土力学性能的主要指标之一。本试验参考《普通混凝土力学性能试验方法标准GB 50081—2002》计算不同应变率下的弹性模量，结果如图9所示。

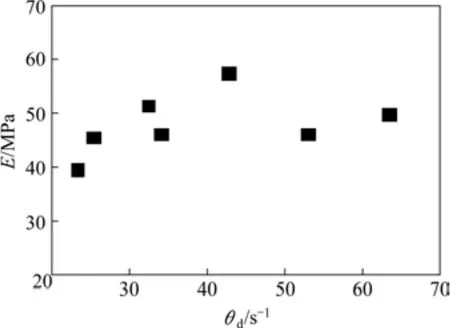
图9 SCC的动态弹性模量与应变率的关系Fig. 9 Relationship between dynamic elastic modulus of SCC and strain rate

从图9中可以看出，SCC动态弹性模量的应变率相关性较差。弹性模量随应变率的变化离散性较大，这可能是由于波动效应导致初始阶段试件内部应力均匀性较差。但同时发现，SCC的动态弹性模量基本稳定在40～60 GPa的范围，其平均值为48 GPa，比静态弹性模量约高31.5%。

2.5 比能量吸收

比能量吸收可用来表征SCC材料的韧性，定义为单位体积 SCC吸收应力波能量的大小。可用式(6)～(9)计算得到：

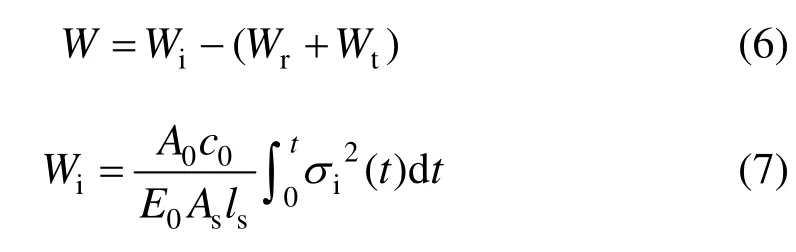
式中：W为SCC的比能量吸收；Wi，Wr和Wt分别为入射波、反射波和透射波所携带的能量；σi(t)，σr(t)和σt(t)分别为入射波应力、反射波应力和透射波应力[21]。

根据上述公式，计算得到不同应变率下SCC的比能量吸收值随应变的变化规律，如图10所示。

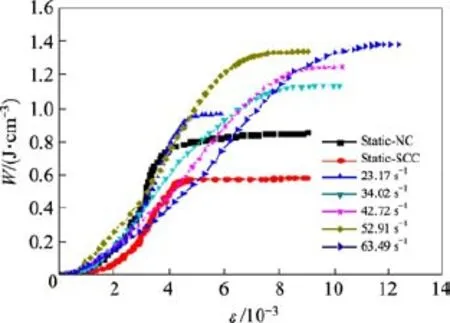
图10 不同应变率下充填层SCC的比能量吸收Fig. 10 Specific energy absorption of SCC under varied strain rates

由图10可以看出，SCC的比能量吸收随应变的变化大体上都呈“S”形曲线，即比能量吸收随应变的增大呈现先慢后快最后趋于稳定的增长特点。累积的比能量吸收随应变率的增大而增大，说明应变率的增大使 SCC试件破坏时吸收更多的能量。另外，在静载下强度等级同为C40的普通混凝土(NC)和自密实混凝土(SCC)比能量吸收规律也有所差异。在试件裂缝的形成和快速发展阶段(对应曲线的快速上升部分)，NC的比能量吸收速率始终大于SCC，最终试件破坏时的累积比能量吸收值也高于SCC。SCC试件由于浆体含量较多导致硬化后脆性更大，且自密实浇筑方法使得内部更为致密，原生裂缝较少。在外部静荷载作用下，可扩展的裂缝较少，且容易沿界面过渡区迅速连通脆性较大的基体而形成贯通裂缝，在整个过程中能量吸收的途径有限，导致比能量吸收速率和最终的累积比能量吸收都低于NC。图11给出了SCC比能量吸收的累积值(Wmax)随应变率对数的变化规律，并通过拟合计算得到公式(10)，其中R2=0.954 4，拟合结果与试验结果具有较高的相关性。

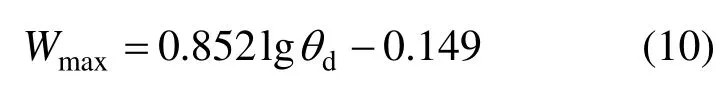
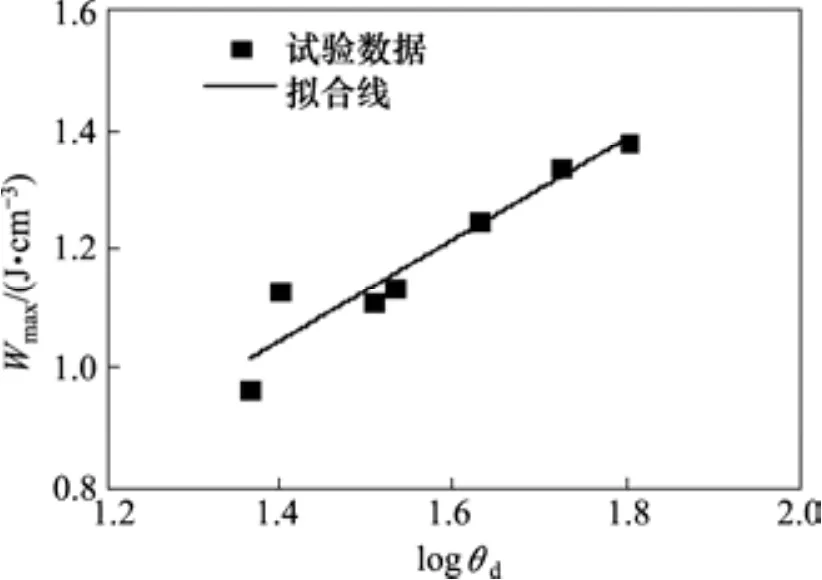
图11 充填层SCC累积比能量吸收与应变率关系Fig. 11 Relationship between maximum of specific energy absorption and strain rate

3 SCC动态本构模型

3.1 模型的建立

根据应变等价性假说，在一维应力状态下材料的本构关系可表示为[22−23]：

式中：σ为有效应力；E为弹性模量；ɛ为应变；D为损伤变量。

将SCC的损伤破坏视为一个连续发展的过程，并假设: 1) SCC 宏观上为各向同性，破坏时损伤各向等效发展；2) SCC由无数细小微元组成，这些微单元包含许多随机分布的微观裂纹和微小缺陷，其损伤发展服从Weibull分布，由此可得损伤变量D的表达式如式(12)所示[23]：

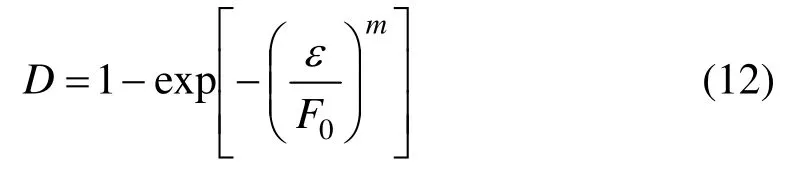
式中：F0和m为与损伤分布相关的参数。

根据式(11)和式(12)，可得式(13)：

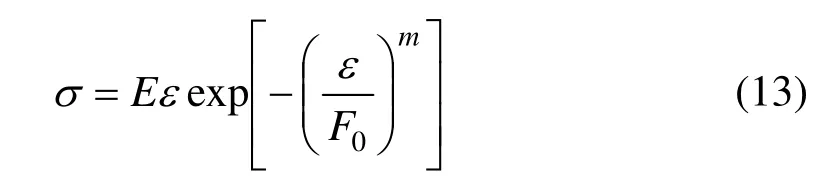
根据混凝土应力应变行为满足的边界条件[10,23]，可得到参数m，F0表达式如下：

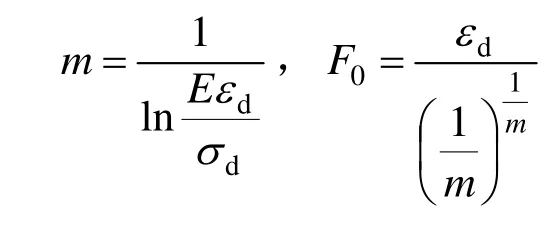
将参数 F0表达式代入式(13)，可得单参数(m)的SCC动态本构模型，如式(14)所示：

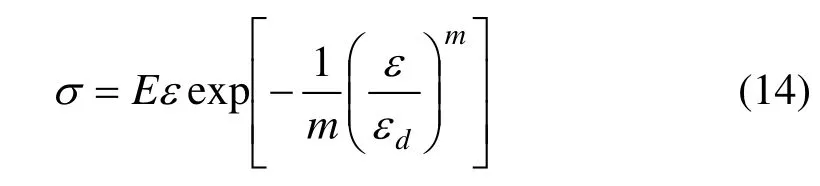
定义临界损伤Dcr为SCC应力应变曲线上的动态峰值应力(或峰值应变)对应的损伤变量。结合式(12)及F0的表达式可推导出Dcr与应变的关系式：

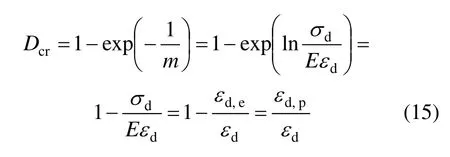
由式(15)可进一步得到m与各应变之间的关系如式(16)所示：

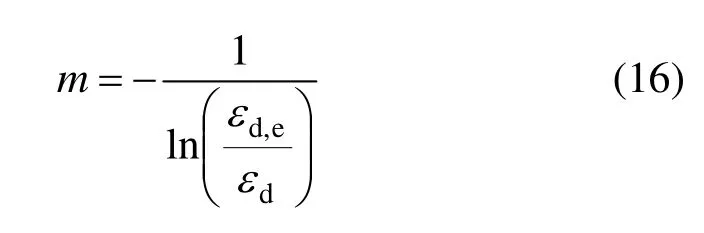
其中：σd为动态峰值强度；εd为动态峰值应变；εd,e和εd,p分别为动态峰值应变处对应的弹性应变和塑性应变。

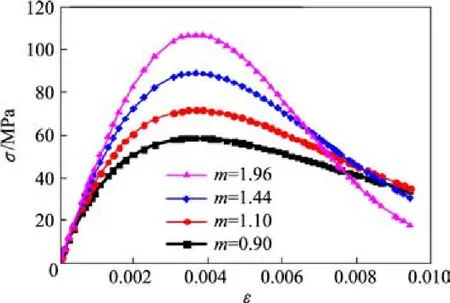
图12 参数m对应力−应变曲线的影响Fig. 12 Influence of m on stress-strain curves

当SCC延性增大时，其峰值应变范围内的弹性应变减小，即 εd,e/εd减小。由于 εd,e/εd<1，由式(16)可知，此时m值减小。图12描述了不同m值对应的SCC应力应变曲线。其中，m的取值0.90，1.10，1.44和1.96分别对应弹性变形为峰值应变的1/3，40%，50%和60%。

由图 12可知，在相同峰值应变下，m的减小会引起 SCC应力−应变曲线下降段越来越趋于平缓，材料的延性提高。因此，该本构模型参数m可较好地反映SCC的脆性(或延性)程度。

3.2 应变率对参数m的影响

根据SCC的应力应变曲线计算得到m值随应变率的变化规律如图13所示。

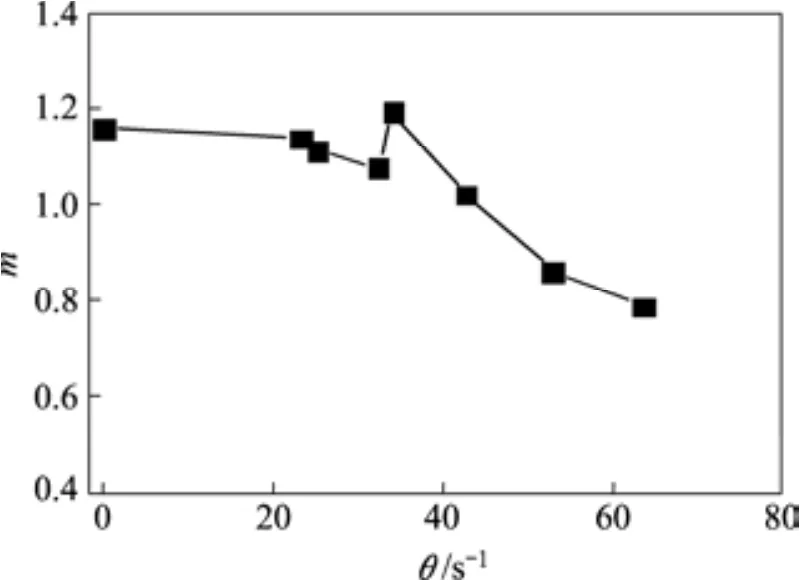
图13 应变率对不同试件m值的影响Fig. 13 Influence of strain rates on parameter m

由图13可知，在静荷载下，参数m处于较高水平，随应变率的增大，m整体呈降低趋势。在应变率低于34.02 s−1左右时，m随应变率增大而缓慢下降；当应变率高于34.02 s−1时，m随应变率增大而急剧下降。这说明SCC在应变率较低时，峰值应变处弹性应变占比较大。随着应变率的增大，试件的破坏模式发生变化，在冲击荷载作用下的裂纹数增多，塑性变形占比增大。这与前文对试件破坏形态的分析结果一致。

3.3 本构模型的验证

计算得到 SCC本构模型参数及拟合曲线与试验结果的对比分别列于表3和图14。

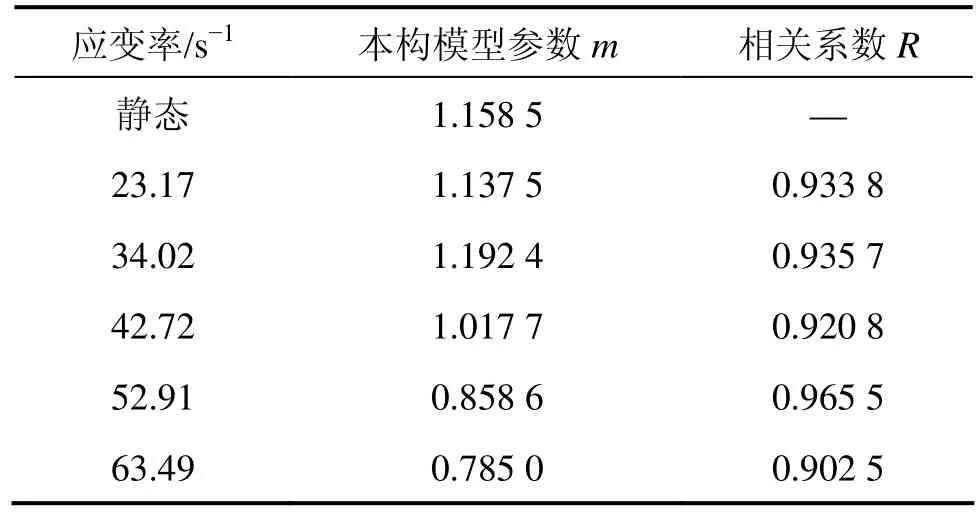
表3 SCC本构模型相关参数值计算结果Table 3 Parameters of constitutive model for SCC

图14 本构模型结果与试验结果的对比Fig. 14 Comparison of fitting curve and experimental data

由表3和图14可知，拟合结果与试验结果的相关系数均在0.9 以上，说明拟合结果与试验结果的吻合度较好。本构模型对峰值强度前应力−应变曲线的拟合效果优于峰值强度后效果。模型对峰值强度的拟合结果准确度很高，拟合结果与试验结果最大相差4.9%。对各应变率，参数m大体随应变率的增大而减小。这说明随应变率的增大，试件的破坏趋于延性破坏，这与前面的讨论结果一致。

4 结论

1) 充填层SCC峰值强度和峰值应变都随应变率的增大而增大；与普通混凝土相比，充填层SCC动态峰值强度表现出更为显著的应变率敏感性。

2) 充填层 SCC 动态强度增长因子(σd/σs)和应变增长因子(εd/εs)与应变率比值的对数(log(θd/θs))存在良好的线性相关性，且峰值应变的应变率敏感性大于峰值强度的应变率敏感性。

3) 在所测应变率范围内，充填层SCC弹性模量基本处于40～60 GPa之间，不具有明显的应变率相关性。

4) 充填层 SCC比能量吸收随应变增加而呈“S”形增长趋势，且比能量吸收的最大值随应变率对数的增大而线性增加。

5) 基于应变等价性假说和统计损伤理论建立了SCC动态本构模型，参数m随应变率增加而减小，与试验结果吻合较好。

[1] Bischoff P H, Perry S H. Compressive behaviour of concrete at high strain rates[J]. Materials & Structures.1991, 24(6): 425−450.

[2] Dilger W H, Koch R, Kowalczyk A R. Ductility of plain and confined concrete under different strain rates[J].Journal of the American Concrete Institute, 1984, 81(1):73−81.

[3] Grote D L, Park S W, Zhou M. Dynamic behavior of concrete at high strain rates and pressures: I. experimental characterization[J]. International Journal of Impact Engineering, 2001, 25(1): 869−886.

[4] Suaris W, Shah S P. Properties of concrete subjected to impact[J]. Journal of Structural Engineering, 1983,109(7): 1727−1741.

[5] Yousef Al-Salloum, Tarek Almusallam, Ibrahim S M, et al. Rate dependent behavior and modeling of concrete based on SHPB experiments[J]. Cement and Concrete Composites, 2015, 55: 34−44.

[6] Andreas Leemann, Roman Loser, Beat Münch. Influence of cement type on ITZ porosity and chloride resistance of self-compacting concrete[J]. Cement & Concrete Composites, 2010, 2: 116−120.

[7] Leemann A, Münch B, Gasser P, et al. Influence of compaction on the interfacial transition zone and the permeability of concrete[J]. Cement & Concrete Research,2006, 36(8): 1425−1433.

[8] 向俊, 赫丹, 曾庆元. 水泥沥青砂浆劣化对板式轨道动力学性能的影响[J]. 中南大学学报(自然科学版), 2009,40(3): 791−796.XIANG Jun, HE Dan, ZENG Qingyuan. Effect of cement asphalt mortar disease on dynamic performance of slab track[J]. Journal of Central South University (Science and Technology), 2009, 40(3): 791−796.

[9] 李培刚, 刘学毅, 黎国清. CA砂浆脱空对桥上单元板式轨道动力特性的影响研究[J]. 中国铁道科学, 2014,35(3): 20−27.LI Peigang, LIU Xueyi, LI Guoqing. Influence of CA mortar void on dynamic characteristics of unit slab track on bridge[J]. China Railway Science, 2014, 35(3): 20−27.

[10] 谢友均, 傅强, 龙广成, 等. 基于 SHPB试验的高速铁路 CRTSII型 CA砂浆动态性能[J]. 中国科学(技术科学), 2014, 44(7): 672−680.XIE Youjun, FU Qiang, LONG Guangcheng, et al.Dynamic mechanical properties of CRTS II type CA mortar for high-speed railway based on SHPB test[J].Scientia Sinica Technologica (Technological Sciences),2014, 44(7): 672−680.

[11] 李为民, 许金余. 玄武岩纤维对混凝土的增强和增韧效应[J]. 硅酸盐学报, 2008, 36(4): 476−481.LI Weiming, XU Jinyu. Strengthening and toughening in basalt fiber-reinforced concrete[J]. Journal of the Chinese Ceramic Society, 2008, 36(4): 476−481.

[12] 刘越. 混凝土材料承载能力及破坏模式的细观分析模型[J]. 中国铁道科学, 2000, 21(1): 65−75.LIU Yue. Micromechanical model of load-bearing capacity and collapse behavior of concrete[J]. China Railway Science, 2000, 21(1): 65−75.

[13] 江伏. 应用 SHPB试验对橡胶粉混凝土动力性能的研究[D]. 长沙: 湖南大学, 2007.JIANG Fu. The research on the dynamic behavior of rubberized concrete by using split Hopkinson pressure bar[D]. Changsha: Hunan University, 2007.

[14] 许金余, 李为民, 杨进勇, 等. 纤维增强地质聚合物混凝土的动态力学性能[J]. 土木工程学报, 2010, 43(2):127−132.XU Jinyu, LI Weimin, YANG Jingyong, et al. Dynamic properties of fiber reinforced geopolymeric concrete[J].China Civil Engineering Journal, 2010, 43(2): 127−132.

[15] 严少华, 段吉祥, 尹放林, 等. 高强混凝土 SHPB试验研究[J]. 解放军理工大学学报(自然科学版), 2000, 1(3):6−9.YAN Shaohua, DUAN Jixiang, YIN Fanglin, et al. SHPB test on high-strength concrete[J]. Journal of PLA University of Science and Technology (Science and Technology), 2000, 1(3): 6−9.

[16] ZHANG M, WU H J, LI Q M, et al. Further investigation on the dynamic compressive strength enhancement of concrete-like materials based on split Hopkinson pressure bar tests. Part I: Experiments[J]. International Journal of Impact Engineering, 2009, 36(12): 1327−1334.

[17] ZHANG W H, ZHANG Y S. Research on the static and dynamic compressive properties of high performance cementitious composite (HPCC) containing coarse aggregate[J]. Archives of Civil & Mechanical Engineering, 2015, 15: 711−720.

[18] Atchley B L, Furr H L. Strength and energy absorption capabilities of plain concrete under dynamic and static loadings[J]. Am Concrete Inst Journal & Proceedings,1967, 64: 745−756.

[19] Watstein D. Effect of straining rate on the compressive strength and elastic properties of concrete[J]. ACI J, 1953,49: 729−744.

[20] 张志刚, 孔大庆, 宫光明, 等. 高应变率下混凝土动态力学性能SHPB实验[J]. 解放军理工大学学报(自然科学版), 2007, 8(6): 611−618.ZHANG Zhigang, KONG Daqing, GONG Guangming, et al. Dynamic mechanical behavior of concrete under high strain rate using SHPB[J]. Journal of PLA University of Science and Technology (Science and Technology), 2007,8(6): 611−618.

[21] 夏昌敬, 谢和平, 鞠杨. 孔隙岩石的SHPB试验研究[J].岩石力学与工程学报, 2006, 25(5): 896−900.XIA Changjing, XIE Heping, JU Yang. SHPB test on porous rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(5): 896−900.

[22] Lemaitre J. How to use damage mechanics[J]. Nuclear Engineering & Design, 1984, 80(2): 233−245.

[23] 吴政, 张承娟. 单向荷载作用下岩石损伤模型及其力学特性研究[J]. 岩石力学与工程学报, 1996, 15(1): 55−61.WU Zheng, ZHANG Chengjuan. Investigation of rock damage model and its mechanical behavior[J]. Chinese Journal of Rock Mechanics and Engineering, 1996, 15(1):55−61.