基于隐式参数化模型的白车身轻量化设计∗

王登峰，蔡珂芳，马明辉，张 帅

(1.吉林大学，汽车仿真与控制国家重点实验室，长春 130022； 2.中国第一汽车股份有限公司技术中心，长春 130011)

前言

面对日益突出的能源和环境问题，轻量化设计已受到各大汽车厂商的关注。大量研究表明，汽车质量每减少10%，燃油消耗可降低6%～8%，尾气排放将减少5%～6%[1－2]。白车身占整车质量的20%～30%，可见其在整车轻量化设计方面有着重要的潜能[3]。目前，轻量化设计主要通过3种方法实现:材料轻量化，主要有高强度钢、轻质金属材料(如镁铝合金)和非金属材料(碳纤维复合材料，高强度塑料)；工艺轻量化，采用先进的加工工艺方法，如液压成型、激光拼焊和柔性轧制差厚板；结构轻量化，通过拓扑优化、尺寸优化、形状优化和形貌优化等方法优化结构。然而在结构优化领域，很多研究通过零部件厚度尺寸优化来实现轻量化设计[4－5]。由于白车身由复杂的梁结构和钣金件构成，故对其进行形状和尺寸优化能有效提升其性能和降低其质量。尽管形状优化在结构优化领域有很多优势，但由于网格单元的畸变和拓扑连接关系不能更新的限制，增加了形状设计变量定义的难度。因此，本文中采用隐式化参数建模的方法来避免有限元模型的网格畸变，做到随动地更新零部件之间的拓扑连接关系。

在白车身早期开发阶段，一般需要大量的待选方案，甚至须考虑完全不同的组件替换和载荷传递路径，按照传统的设计方法，反复修改CAD模型并进行相应的CAE分析，耗费大量资源。然而隐式参数化建模技术能将CAE分析融入早期的设计阶段，提前分析、评价和优化白车身轻量化设计，实现CAE分析驱动设计的理念。

近年来，隐式参数化建模技术和多目标优化设计方法在车身轻量化领域得到了较大的发展。文献[6]中通过多学科轻量化设计方法，对参数化白车身进行了厚度尺寸等优化，使白车身质量减轻12kg，轻量率达到4.5%。文献[7]中使用灵敏度分析方法筛选66个白车身零件板厚作为设计变量，通过遗传优化算法对参数化车身进行轻量化设计，车身质量减轻19.4kg，轻量率达6.4%。文献[8]中采用分布优化设计方法，逐步改善了车身的静动态性能，得到了最优轻量化方案。文献[9]中在保证车身性能不降低的前提下，利用隐式参数化技术和多目标优化方法，实现了车身减轻 32.41kg，达到7.63%。尽管隐式参数化建模和多目标优化方法在轻量化方面有较好的研究基础，但针对白车身整体尺寸优化和梁结构截面形状优化的研究很少。

本文中通过SFE-CONCEPT建立了隐式参数化白车身模型，提出了CAE分析驱动设计的理念，可快速实现大几何变形并保证智能连接的一致性，同时实现网格的自动生成和结构的参数化。首先在参数化平台基础上，合理优化车身整体尺寸，保证乘坐空间改善的同时车身性能不下降；然后通过改善梁结构截面尺寸，提高白车身静动态性能；最后通过优化板料厚度，降低白车身整体质量，实现轻量化设计。

1 隐式参数化建模与模型验证

1.1 隐式参数化建模

传统的参数化建模多为显式参数化建模技术，通常利用结构参数作为输入，而非用数学关系来定义结构模型，从而很难实现较大的几何变形和零件间复杂装配关系的更新。而隐式参数化技术不仅能快速建模，而且能通过定义各零件间的映射关系，实现参数化装配。SFE-CONCEPT采用隐式参数化技术，主要通过基点的坐标位置、基线的曲率和截面的形状定义模型的几何结构。通过上述基本元素(见图1)，可快速建立具有参数化能力的梁结构和曲面，进而完成复杂参数化模型的建立。各个几何体之间通过拓扑映射技术建立逻辑连接，从而实现参数化装配。因此当模型中某个参数发生改变，与之相关连的参数也会相应地变化，保证了零件之间原有的连接关系的稳定性和模型整体的连续性，而无须像其他软件那样逐个修改与之相邻的部件[10－11]，图2示出隐式参数化与显式参数化的区别。由图2(a)可见，显式参数化建模时，随着门槛梁的移动变化，地板、座椅横梁和B柱接头均没有发生变化，说明各部件之间的拓扑连接关系丢失。由图2(b)可见，通过隐式参数化建模，随着门槛梁的移动，地板、座椅横梁和B柱接头均跟着移动，始终保持着各部件之间的拓扑连接关系，这为后期的白车身整体尺寸变化和梁结构截面形状变化提供了有效的技术支持。

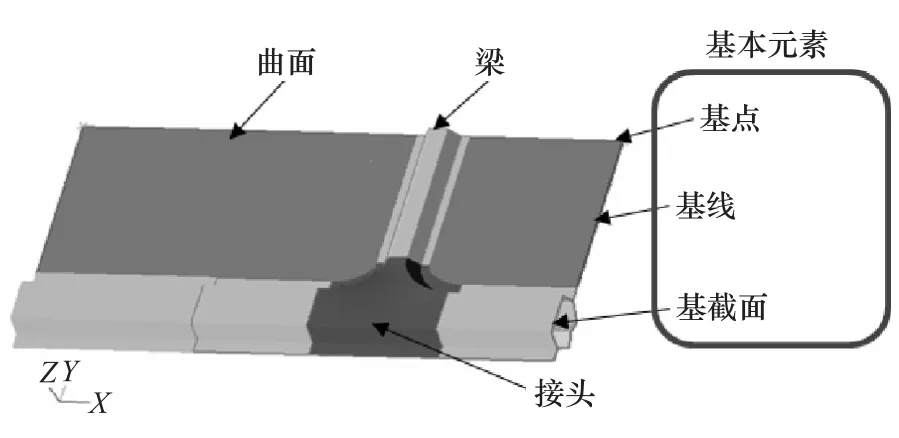
图1 隐式参数化建模基本元素

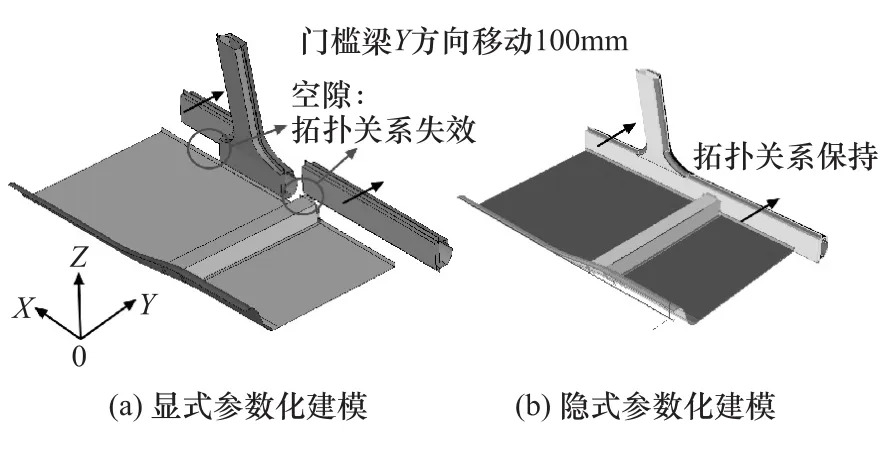
图2 隐式参数化与显式参数化建模的区别

以经实验验证的有限元模型为基准，利用SFECONCEPT建立隐式参数化白车身模型。首先为方便建模，将白车身分为四门两盖、侧围、前端、后端、地板与顶棚和风窗玻璃6个子系统；其次根据各子系统的整体布局，合理布置基点；然后根据各零件的曲率形状，结合基点建立具有特征曲率的基线；最后根据零件的几何特征，结合有限元模型的截面，建立基截面，通过上述基本元素的建立，完成各个子系统的创建。通过MAP映射连接技术，封装子系统和装配参数化白车身模型。隐式参数化白车身模型的建模过程如图3所示，图4为隐式参数化白车身模型。

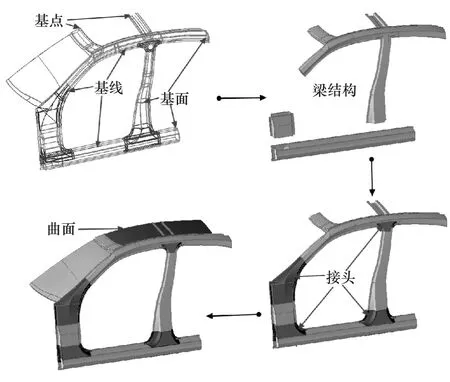
图3 隐式参数化白车身建模流程

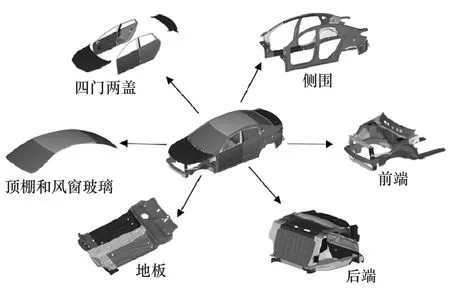
图4 隐式参数化白车身模型

1.2 模型验证

根据参数化白车身模型，通过SFE-CONCEPT自带的有限元模型自动生成功能，可快速生成满足分析要求的有限元模型，且包括材料、属性、加载、约束和焊点等信息。共离散为531 062个单元和541 526个节点，得到的白车身有限元模型如图5所示。表1列出了原白车身有限元模型(通过实验验证)与SFE-CONCEPT生成的有限元模型在相同工况条件下得到的车身静动态性能和质量对比。由表1可以看出，原白车身有限元模型与SFECONCEPT所生成的有限元模型最大相对误差不超过5%，具有良好的一致性。说明建立的参数化模型是正确的，可用来进行下一步的轻量化多目标优化。

图5 SFE白车身有限元模型

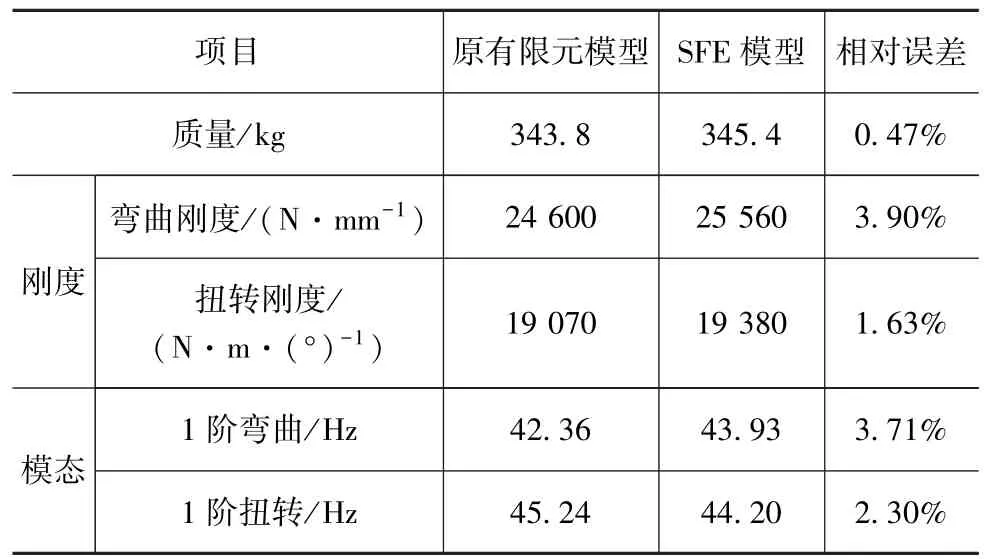
表1 原有限元模型与SFE模型性能对比

2 白车身整体尺寸优化

随着人们对乘坐空间舒适性的需求，基于原有车型改进空间尺寸不仅能满足需求，且能降低开发成本。

2.1 确定设计变量与DOE分析

通过SFE-CONCEPT建立白车身参数化模型，利用基点坐标定义白车身长、宽、高变量，车身中的各个部件的拓扑关系也会随整车尺寸的变化进行随动更新；通过调整基线曲率和截面位置，能细化零件局部特征，使车身整体变形具有良好的连续性和有效性。图6给出了各个变量的范围和变化方向。以车身弯曲刚度、扭转刚度、1阶弯曲1阶扭转模态和质量为优化目标进行多目标优化设计。

为使所采用的空间分布均匀合理，使用正交实验和优化的拉丁超立方相结合的方法生成DOE样本，针对3个设计变量及其对应的取值范围，总计选取100个计算样本，包括20个检验样本。通过Nastran求解器分别计算车身的弯扭刚度、1阶弯曲1阶扭转模态，并统计相应的模型质量，为后续近似模型的建立提供数据结果。

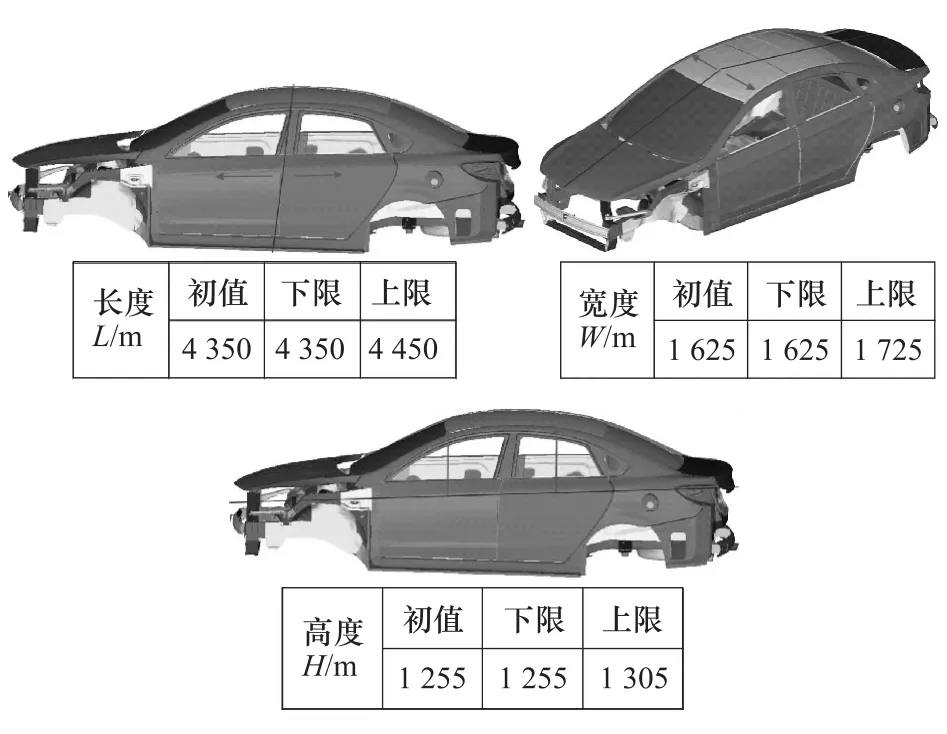
图6 整体尺寸变量范围及方向

2.2 整体尺寸多目标优化设计

为提高优化效率，采用径向基RBF近似模型替代仿真模型建立设计变量与各个响应间的关系，其拟合精度可通过决定系数R2来验证:

式中:N为检验样本点数目；yi为第i个响应的仿真值；yi为第i个响应的近似模型预测值；y为仿真值的平均值。

R2值越接近于1，表明近似模型有较高的可靠度，经计算得到质量、弯曲刚度、扭转刚度、1阶弯曲模态频率和1阶扭转模态频率对应的决定系数R2分别为 0.967，0.934，0.958，0.949 和 0.963，其中质量和弯曲刚度近似模型的检验精度如图7所示。可见所有近似模型都能满足优化要求。

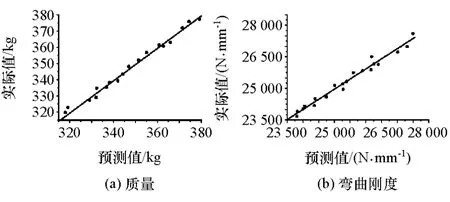
图7 近似模型精度检验

以1阶弯曲模态不低于43Hz和1阶扭转模态不低于43.2Hz为约束；以弯扭刚度最大和车身质量最小为优化目标，由于该优化阶段更注重弯扭刚度的提高，所以弯扭刚度比车身质量取更高的权重。采用非支配遗传算法(NSGAII)进行多目标优化，其优化数学模型如式(2)所示，优化结果见表2。

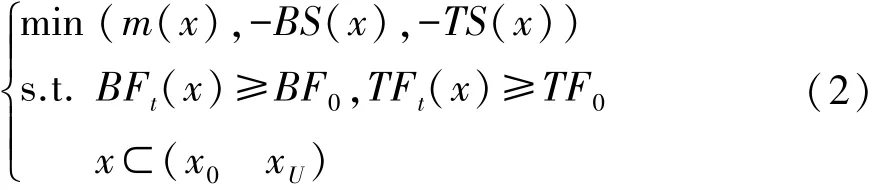
式中:m(x)为白车身总质量；BS(x)和TS(x)分别为白车身弯曲和扭转刚度；BF(x)和TF(x)分别为白车身1阶弯曲和1阶扭转频率；BF0和TF0为对应白车身初始1阶弯曲1阶扭转模态频率；x为白车身整体尺寸设计变量，对应的x0和xU分别为其下限和上限值。

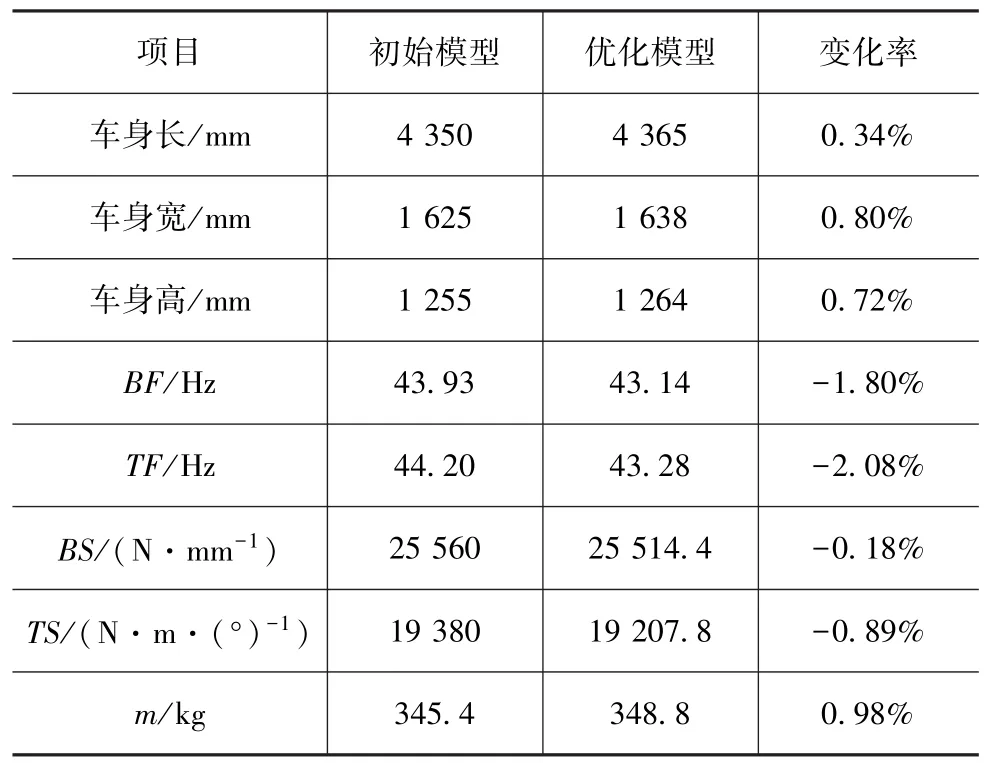
表2 白车身整体尺寸优化结果

3 白车身梁结构截面形状优化

白车身结构为骨架式结构，主要由梁结构组成，起承载和支撑作用，因此对白车身静动态性能有重要影响。在整体尺寸优化基础之上，对梁结构截面进行形状优化可有效地提高白车身性能和控制其质量的增加。该阶段优化以提升白车身性能为主，因此以车身质量为约束，以其1阶弯曲模态频率、1阶扭转模态频率、弯曲刚度和扭转刚度为目标进行多目标优化。

3.1 确定设计变量及DOE分析

选取车身结构中主要承载的梁结构为优化对象，共确定了8个对车身整体性能影响较大的设计变量。具体涉及的梁结构部件如图8所示，表3对所涉及的形状设计变量进行了详细的描述，其中最初设计值用0表示。然后使用正交实验和优化的拉丁超立方相结合的方法生成用于DOE计算的样本，共生成120个样本，其中20个检验样本。

图8 参与设计的梁结构在车身中的分布位置

表3 梁结构截面形状设计变量

3.2 梁结构截面形状优化

使用上述DOE样本搭建近似模型时，由于这些设计变量涉及到形状非线性变量，对白车身的静动态性能表现为非线性影响，所以选择径向基神经网络法(RBF)构造近似模型并采用交叉验证的方法验证该近似模型的准确性。1阶弯曲1阶扭转模态频率的决定系数R2分别为94.8%和93.2%，弯曲刚度、扭转刚度和质量的决定系数R2分别为96.6%，97.2%和98.7%。所以近似模型的可靠性非常高。同样使用非支配遗传算法(NSGAII)进行多目标优化，其具体优化流程如图9所示，得到的优化结果见表4。

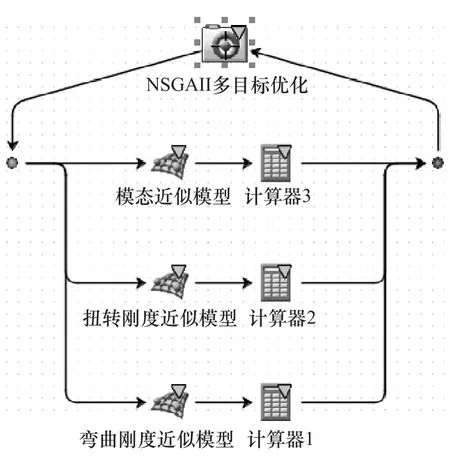
图9 多目标优化分析流程

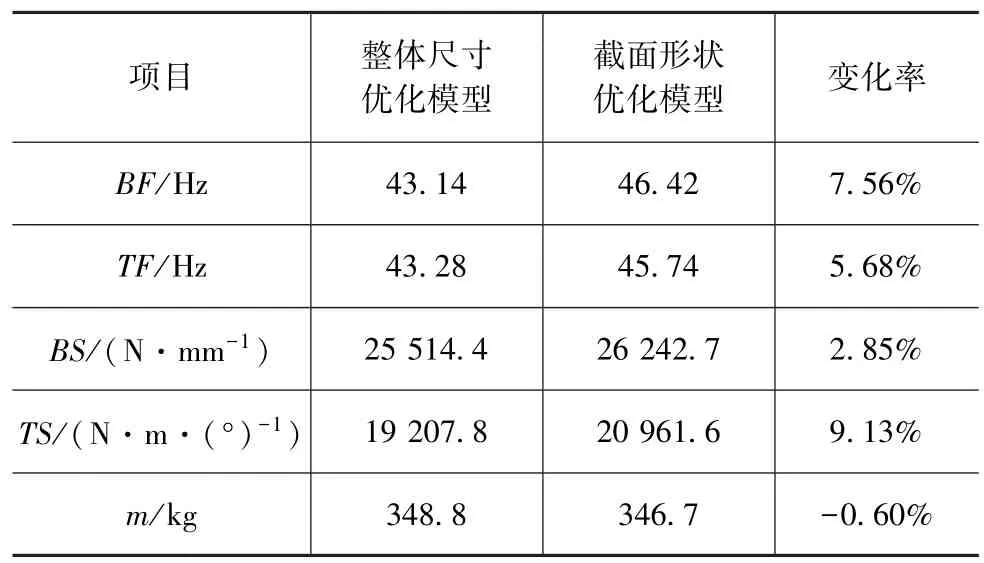
表4 梁结构截面形状优化结果

4 白车身部件厚度尺寸优化

在上述截面形状优化的模型基础之上，选取白车身关键结构板料厚度为设计变量，旨在通过降低上述梁结构截面形状优化所提升的白车身性能来补充质量设计，使车身性能不低于初始模型的前提下最大限度地实现轻量化。

4.1 设计变量的确定与DOE分析

由于各部件对车身性能与质量影响程度不一样和此阶段优化涉及的设计变量较多，故为改善计算效率和优化效果，须筛选出对其性能影响不敏感但对其质量影响敏感的设计变量，做到牺牲最小的性能，实现最有效的轻量。为避免直接灵敏度分析造成只关注性能或质量所带来的不合理筛选，本文中采用了一种相对灵敏度的计算方法来筛选设计变量，同时考虑了性能和轻量的双重指标。

在灵敏度分析方法中，设计变量vi与设计目标g之间的关系可以表示为g＝G(vi)，当设计变量vi发生变化时，相应的设计目标将产生变化:

当设计变量变化同样的值时，即Δvi＝Δ时，而设计目标Δg各不相同，因此可以定义为设计目标g对设计变量vi的直接灵敏度。

该研究定义了质量/刚度对设计变量的灵敏度，即质量灵敏度与刚度灵敏度的比值来对板料设计变量进行筛选，相对灵敏度表达式为

r值越大表明该部件对质量影响较敏感，而对性能影响较小，这样可通过牺牲较小的性能，减轻较多的质量。

通过相对灵敏度方法对白车身56个设计变量进行筛选，最终确定32个对质量影响较大、而对性能影响较小的设计变量，具体部件(黑色部分)在白车身中的位置如图10所示。表5列出了相对灵敏度较大的零部件，对以后的轻量化设计提供了一定的指导。

图10 板料厚度优化的部件(黑色部分)

通过筛选的32个厚度变量，采用正交实验和优化的拉丁超立方结合的方法生成用于DOE计算的样本，共生成160个样本，其中20个检验样本。

4.2 白车身板料厚度优化

由于厚度变化对车身性能的影响近似线性，故使用常用的Kriging方法为DOE样本构建近似模型，采用交叉验证的方法验证近似模型，其中1阶弯曲1阶扭转模态频率的决定系数R2分别为97.6%和98.2%，弯曲刚度、扭转刚度和质量的决定系数R2分别为97.5%、98.4%和97.8%。可见利用近似模型完成多目标优化是可靠的。定义序列二次规划法(SQP)的最大迭代次数为80，收敛精度为1.0×10－6，以质量最小为目标，以优化后性能不低于初始性能为约束，进行多目标优化。表6为部分变量优化前后的对比。

表5 部分设计变量的相对灵敏度

4.3 优化前后车身性能对比分析

通过对白车身逐步进行整体尺寸优化、梁结构截面形状优化和关键结构板料厚度优化，最终在保证车身静动态性能的前提下，最大限度地减轻白车身质量，实现轻量化。图11为白车身在轻量化前后的1阶弯曲和1阶扭转模态对比。由图可见，白车身在天窗和前端等局部结构模态有了较大改善。表7为优化前后白车身性能对比。由图可见，在白车身弯曲刚度和扭转刚度分别降低0.2%和0.6%的情况下，白车身1阶弯曲和1阶扭转频率分别改善了5.6%和 9.2%，其质量减轻了 19.9kg，轻量率达5.76%。通过逐步优化方法，白车身在降低质量的同时，改善了其性能，可见这种方法在白车身优化设计中非常有效。

5 结论

(1)以某轿车白车身为研究对象，利用SFECONCEPT建立了隐式参数化白车身模型，通过与已验证的有限元模型进行性能对比，验证了参数化白车身模型的准确性。

(2)结合在质量不增加的情况下性能最好与在满足性能的前提下质量最小的两种轻量化设计方法，通过对参数化白车身模型逐步进行整体尺寸优化、梁结构截面形状优化和关键部件板料厚度优化，有效地完成了白车身轻量化设计。

表6 部分设计变量优化结果

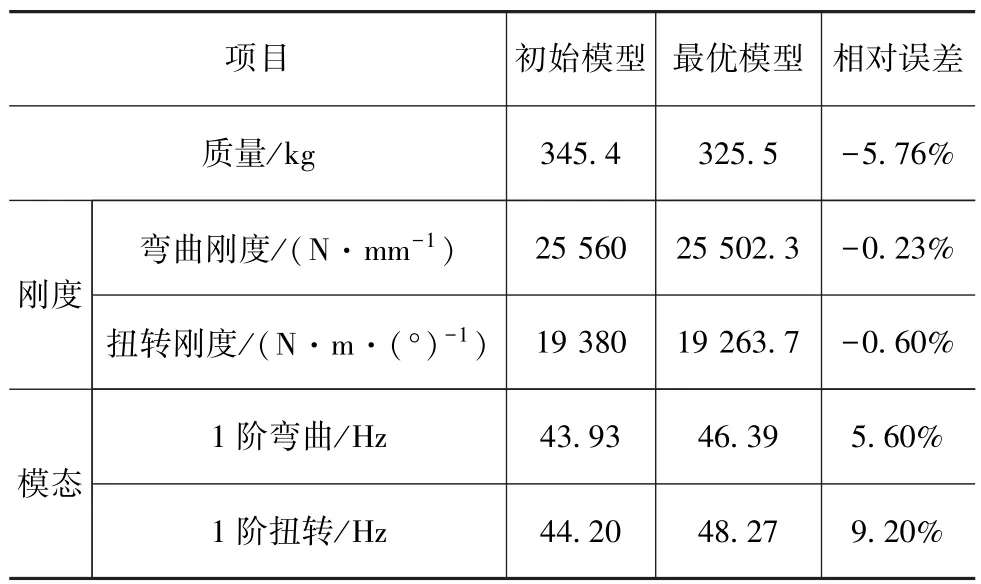
表7 白车身优化前后结果对比

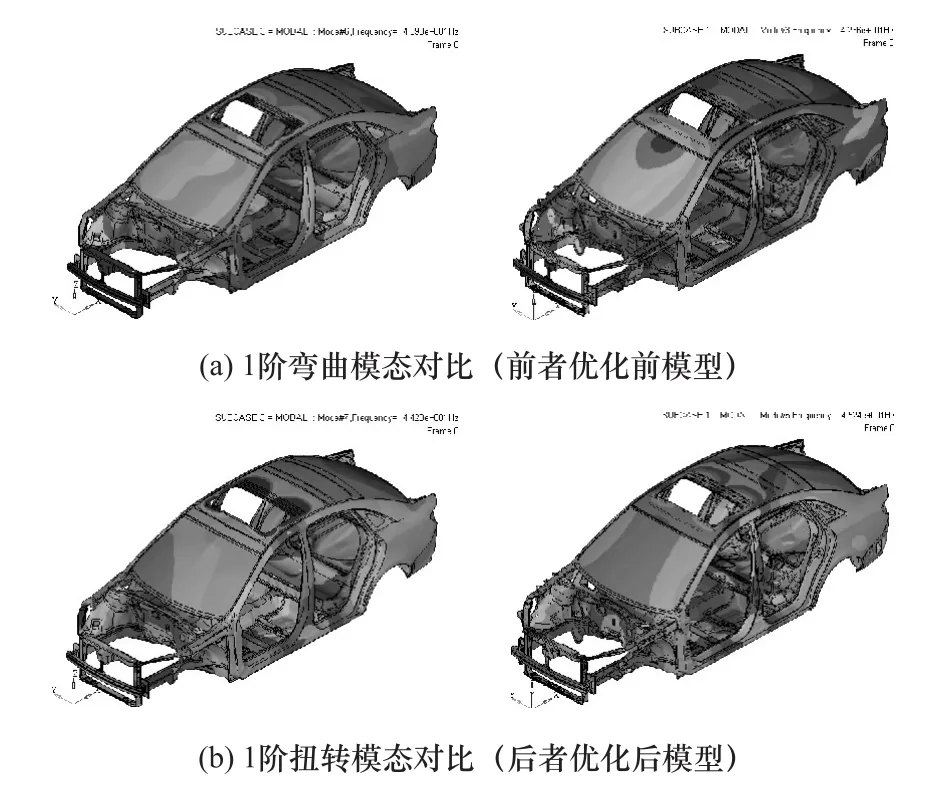
图11 优化前后白车身1阶弯曲1阶扭转模态对比

(3)对设计变量的筛选应用了相对灵敏度的方法，确定了对性能相对不敏感而对质量较敏感的设计变量，从而避免了直接灵敏度只考虑单一性能的缺陷，使优化设计目的性更强。

(4)综合运用隐式参数化建模技术、代理模型方法、NSGAII和SQP优化算法，对白车身进行多因子多目标优化，在保证车身弯扭刚度不降低、车身整体尺寸长、宽和高分别增加了15，13和9mm的前提下，车身1阶弯曲和1阶扭转模态分别改善了5.6%和9.2%，车身质量减轻了 19.9kg，轻量率达5.76%，取得了良好的轻量化效果。

[1] 朱平，张宇，葛龙，等.基于正面耐撞性仿真的轿车车身材料轻化研究[J].机械工程学报，2005，41(9):207－211.

[2] JIA J，ULFVARSON A.A parametric study for the structural behaviour of a lightweight deck[J].Engineering Structures，2004，26(7):963－977.

[3] PAN F，ZHU P， ZHANG Y.Metamodel-based lightweight design of B-pillar with TWB structure via support vector regression[J].Computers ＆ Structures，2010，88(1):36－44.

[4] ZHU P，ZHANGY，CHEN GL.Metamodel-based lightweight design of an automotive front-body structure using robust optimization[J].Proceedings of the Institution of Mechanical Engineers Part D:Journal of Automobile Engineering，2009，223(9):1133－1147.

[5] HUI Y.Lightweight optimization design of car body based on sensitivity and side crash simulation[J].Transactions of the Chinese Society for Agricultural Machinery，2010，41(10):18－22.

[6] 史国宏，陈勇，杨雨泽，等.白车身多学科轻量化优化设计应用[J].机械工程学报，2012，48(8):110－114.

[7] 季枫，王登峰，陈书明，等.轿车白车身隐式参数化建模与多目标轻量化优化[J].汽车工程，2014，36(2):254－258.

[8] 王磊，刘莹，乔鑫.基于正向开发流程的车身轻量化设计[J].汽车工程学报，2015，5(6):461－465.

[9] WANG C Q，WANG D F，ZHANG S.Design and application of lightweight multi-objective collaborative optimization for a parametric body-in-white structure[J].Proceedings of the Institution of Mechanical Engineers Part D:Journal of Automobile Engineering，2016，230(2):273－288.

[10] ZIMMER H.SFE concept reference manual v4.2[G].Berlin，Germany:SFE GmbH，2010.

[11] HÄNSCHKEA，LEEM，et al.Parametric model:knowledgebase for vehicle design to improve the early vehicle attribute assessments[C].International Automotive Body Congress.Jun 17－19，2007，Berlin Germany.