锯齿型石墨烯纳米窄带中量子霍尔体系的电场调控

刘娜 胡边 魏鸿鹏 刘红†

1 引 言

由于石墨烯具有非传统的物理学性质[1,2],以及在纳米电子学中的潜在应用价值,最近几年引起越来越多研究者的关注.人们对石墨烯纳米带的能带结构和电输运性质进行了大量的理论研究.早期理论研究不含自旋劈裂因子和量子输运,单层石墨烯具有无质量Dirac粒子色散关系[3,4],二维窄石墨烯纳米带出现了零能隙和零能边界态[5].2005年,Kane和Mele[6,7]引入两种不同的自旋轨道耦合,即碳原子的内禀自旋轨道耦合作用[8]和外电场引起的Rashba自旋轨道耦合作用[9−12],发现了窄锯齿型石墨烯纳米带的能带结构中4条无散射的边界带和拓扑性非平庸的量子自旋霍尔态[13],开创了新型二维材料拓扑保护边界态理论研究的先河.近年来,各种新型二维拓扑材料被相继发现,其中受拓扑保护的各种边界态的研究激起物理学家、材料学家的广泛兴趣,涌现出大批研究成果.

虽然石墨烯独特的物理学性质在电子学器件中有很大的应用前景,但是其零能隙的特点限制了它的广泛应用.为此,人们不断地探寻打开石墨烯能带的方法.石墨烯打开带隙的方法分为两种类型[14],一类是直接破坏石墨烯的化学结构,导致电子结构受到影响打开带隙,包括掺杂、吸附原子、引入周期性破缺等;另一类是间接破坏石墨烯的结构对称性,引入外场、衬底、自旋轨道耦合作用等打开带隙.Zhang等[15]在双层石墨烯垂直方向加电场,通过调节电场的大小,石墨烯从零能隙慢慢出现带隙.2006年,Son等[16]采用平面内横向电场,使纳米带两边界的静电势不同,破坏两端自旋态的能量简并,导致一种自旋态出现在费米能级处,而另一种自旋态不在费米能级处,呈半金属性,出现单一方向自旋极化电导.

引入自旋轨道耦合作用能打开一个很小的带隙[6,7],而另一个能够打开带隙的哈密顿量是格点在位库仑能.Wang等[17]和Sheng等[18]分别引入了不同的格点在位库仑能,前者采用AB子格点具有不同在位库仑能,而后者则是根据格点距离纳米带边界的远近取不同的在位库仑能,二者计算结果显示的边界带结构有很大不同.这说明格点在位库仑能对边界带的结构影响很大.理论上,格点在位库仑能的大小与格点被电子占据的几率成正比.对于电子空间分布明显不均的边界态来说,应该采用更为合理的、与电子空间分布有关的格点在位库仑能,即自洽在位库仑能[19,20].采用自洽在位库仑能,我们已经详细研究了锯齿型窄纳米带的能带结构和电导[21,22].

本文基于含自旋轨道耦合作用的紧束缚Kane-Mele模型,并采用自洽格点在位库仑能,考虑在锯齿型石墨烯纳米窄带平面内加入横向电场,希望能通过电场调控边界带的能带结构,控制自旋电流,改变系统的量子自旋霍尔体系.计算结果与分析都表明,随电场的强度增强,系统能够从B类量子自旋霍尔体系逐步变为C类普通的量子霍尔体系.

2 理论方法

在以往研究工作的基础上[21,22],加入平面内横向电场,系统的哈密顿量ˆH表示为[18−20,23]:

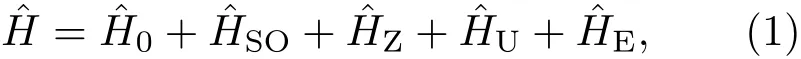
其中

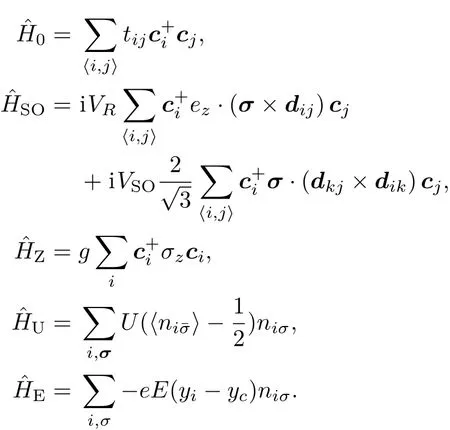
是最近邻格点之间的跃迁项;(ci=(ci↑,ci↓)T)是电子在格点i上的产生(湮没)算符;tij=−2.6 eV是最近邻格点之间的跃迁系数;σ是泡利矩阵,dik是从格点k到格点i的单位矢量,这里格点k是格点i与格点j的共同最近邻;ˆHSO包含原子内部的内禀自旋轨道耦合作用和外电场引起的Rashba自旋轨道耦合作用;ˆHZ是垂直纳米带平面的外磁场引起的塞曼效应;ˆHU是自洽格点在位库仑相互作用[19,20];其中表示在原胞中第i格点上自旋为σ的粒子占据数,⟨niσ⟩是考虑温度效应后,在格点i上自旋为σ的平均粒子占据数;ˆHE是平面内沿y方向上施加的一横向均匀电场的哈密顿作用量,yi是格点i的坐标y分量,yc是纳米带中心的坐标y分量;E为外电场强度参数,文中电场强度的单位是V/nm,取值范围为0—2.0 V/nm.在本文中,其他参数与文献[18,21,22]一致,U=4 eV,VR=0.01t0,VSO=0.02t0,g=0.02 eV.而且我们仍然以仅含8个原子的窄锯齿型石墨烯纳米带为研究对象,其宽度为0.71 nm,几何结构见图1.

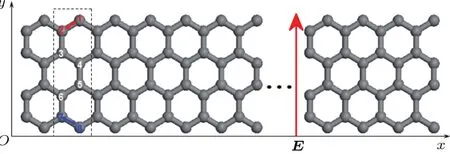
图1 锯齿型石墨烯纳米窄带结构示意图 宽度是8个原子,沿x方向周期平移;虚框内为原胞结构,其中整数1—8是原胞内碳原子的格点指标,垂直向上红色箭头表示外加电场方向Fig.1. Geometric structure of the narrow zigzag graphene nanoribbon(ZGNR)with the width of 8 atoms.Periodic translational direction is along the x-axis.The shadow cube denotes the primitive cell,in which the integers 1–8 denote the site indices of C-atoms.The red vertical arrow denotes the applied electric fi eld.

3 结果与讨论

首先研究电场方向对石墨烯纳米带边界带能带结构的影响,见图2.图2中,E为能量,∆为带隙,a为晶格常数,q为波矢(单位为2π/a),N为边界带的指标,VE为电场强度.可以看出,当外加电场强度较小时,7带和9带交叉点的移动方向随电场方向的不同而不同:当电场为负方向时,它向右移动至q=0.541;当电场为正方向时,它向左移动至q=0.459;原7带和9带交叉点处能级简并,此时发生劈裂,出现较大的带隙,为22.31 meV,因该处的能量低于费米能,故它不是系统的能隙.进一步发现左右费米波矢处的能量和带隙随外加电场方向的变化而变化,原左右能隙成为带隙:当电场为负方向时,左费米波矢的能量高于右费米波矢的能量,左带隙大于右带隙;而当电场为正方向时,左费米波矢的能量低于右费米波矢的能量,左带隙小于右带隙.接着,我们从图2(a1)—(a4)和图2(b1)—(b4)电子占据几率的空间分布中发现,无论所加外电场为正向还是反向,能带结构中自旋向上的8带和10带的空间占据几率分布基本不变,而自旋向下的7带和9带发生较大变化.比较图2(a1)与图2(a3)中q=0.541附近、图2(b1)与图2(b3)中q=0.459附近,原7带与9带上自旋向下的电子分别分布在不同边界1与8格点上,但在引入电场后,7带与9带交叉点处,7带与9带都不再是单一局域一个边界格点的边界带,两个带的空间几率分布发生混合,原能级简并消除;且随波矢的变化,混合效应逐渐消失;同样的情况也发生在8带和10带交叉处,也出现两个不同边界格点的几率分布发生混合的情况,但相对于7带与9带的混合,其强度非常弱,而且很快消失.另外,在左右费米波矢处,即8带与9带、7带与10带的交叉处,原来因自旋简并劈裂而导致的电子几率是两个不同自旋方向的几率的混合,现在电场的加入使得这个混合效应增强,几乎完全反转,但是随q的变化会迅速恢复.

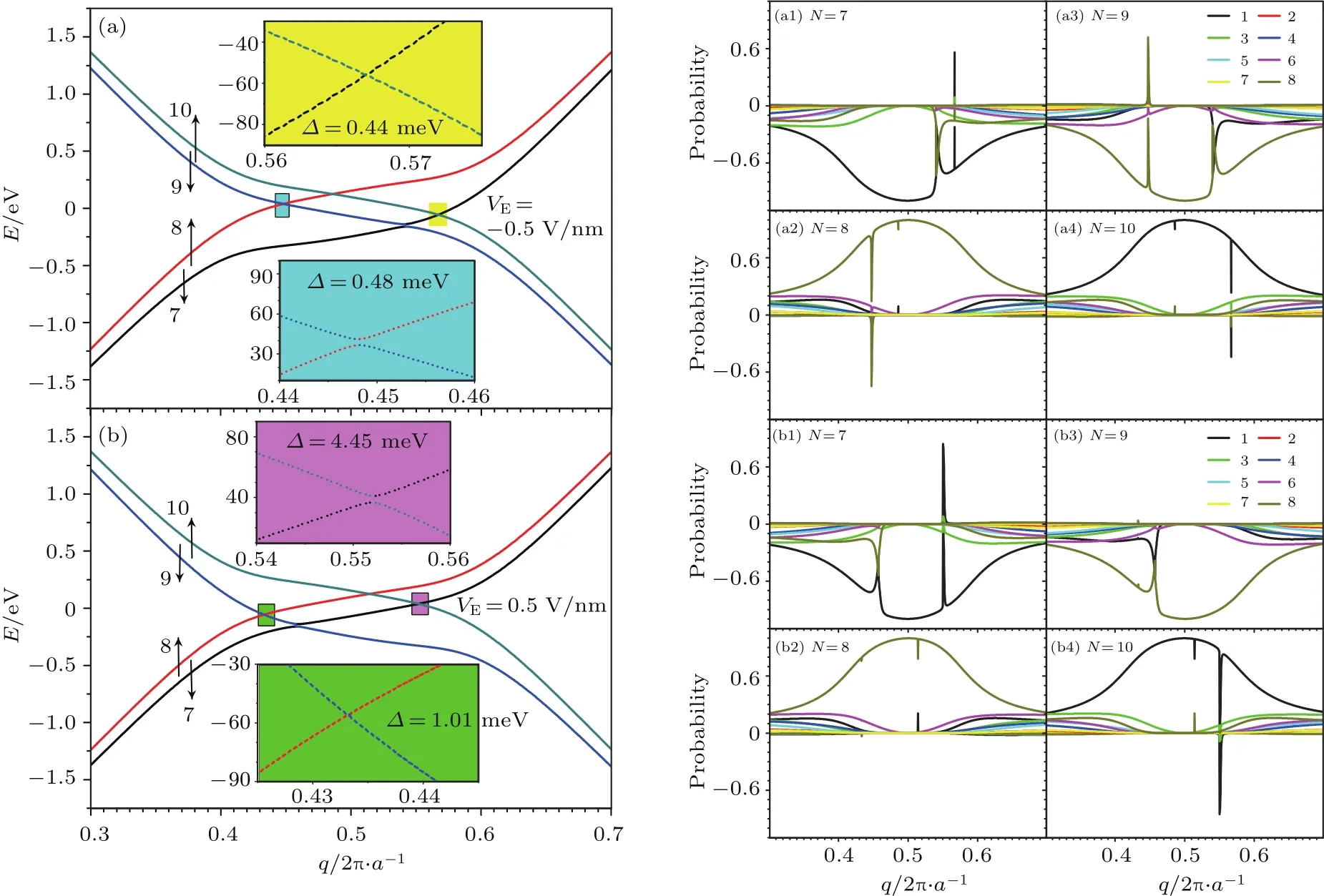
图2 电场强度分别为±0.05 V/nm时4个边界带的能带结构及相应能带上的状态中电子在空间格点占据几率 (a)V E=−0.5 V/nm的能带结构;(b)V E=0.5 V/nm的能带结构;(a1)V E=−0.5 V/nm,能带N=7时电子在空间格点占据几率;(a2)V E=−0.5 V/nm,能带N=8时电子在空间格点占据几率;(a3)V E=−0.5 V/nm,能带N=9时电子在空间格点占据几率;(a4)V E=−0.5 V/nm,能带N=10时电子在空间格点占据几率;(b1)V E=0.5 V/nm,能带N=7时电子在空间格点占据几率;(b2)V E=0.5 V/nm,能带N=8时电子在空间格点占据几率;(b3)V E=0.5 V/nm,能带N=9时电子在空间格点占据几率;(b4)V E=0.5 V/nm,能带N=10时电子在空间格点占据几率;图中整数代表各带的指标,箭头代表各带的自旋方向Fig.2.The band structures of four edge bands and the occupied probabilities at spacial sites of electrons in the edge states under the corresponding electric fi elds±0.05 V/nm:(a)Band structure under V E=−0.5 V/nm;(b)band structure under V E=0.5 V/nm;(a1)occupied probabilities at spacial sites of electrons for the edge band N=7 under V E=−0.5 V/nm;(a2)occupied probabilities at spacial sites of electrons for the edge band N=8 under V E=−0.5 V/nm;(a3)occupied probabilities at spacial sites of electrons for the edge band N=9 under V E=−0.5 V/nm;(a4)occupied probabilities at spacial sites of electrons for the edge band N=10 under V E=−0.5 V/nm;(b1)occupied probabilities at spacial sites of electrons for the edge band N=7 under V E=0.5 V/nm;(b2)occupied probabilities at spacial sites of electrons for the edge band N=8 under V E=0.5 V/nm;(b3)occupied probabilities at spacial sites of electrons for the edge band N=9 under V E=0.5 V/nm;(b4)occupied probabilities at spacial sites of electrons for the edge band N=10 under V E=0.5 V/nm.The integers denote the band indices and the gray vertical arrows denote the spin directions of bands.

同时,虽然7带与9带交叉点随电场方向的不同而朝不同方向发生移动,但是在边界格点上,电子空间占据几率最大达到100%的边界态仍然位于q=0.5处,见图2(a1)—(a4)和图2(b1)—(b4).在没有外电场时,7带与9带交叉点在q=0.5处,其上两个自旋向下电子分别局域在不同的边界格点上,但是速度方向相反,因此在该能量处,两个边界带自旋向下电子贡献的电导总和为零[23].当加入平面内横向电场后,在q=0.5处,7带与9带的能级简并消失,两个局域在不同边界格点的两个边界态电子在能量上分开,见图2(a)和图2(b).在q=0.5处,当电场为−0.5 V/nm时,9带的能量大于7带的能量.故在高能量时,100%在边界格点8上的9带边界态电子贡献自旋向下的正向边界电流;而在低能量处,100%在格点1上的7带边界态电子提供自旋向下的反向边界电流.相反,当电场为0.5 V/nm时,7带的能量高于9带的能量,故在高能量时,边界格点1处的7带边界态电子提供自旋向下的反向边界电流;而在低能量处,在边界格点8上贡献自旋向下的正向边界电流.因此,在高(或低)能量处,可以通过调控电场方向产生不同方向的自旋电流,并且调控自旋向下的电流在不同边界处出现.

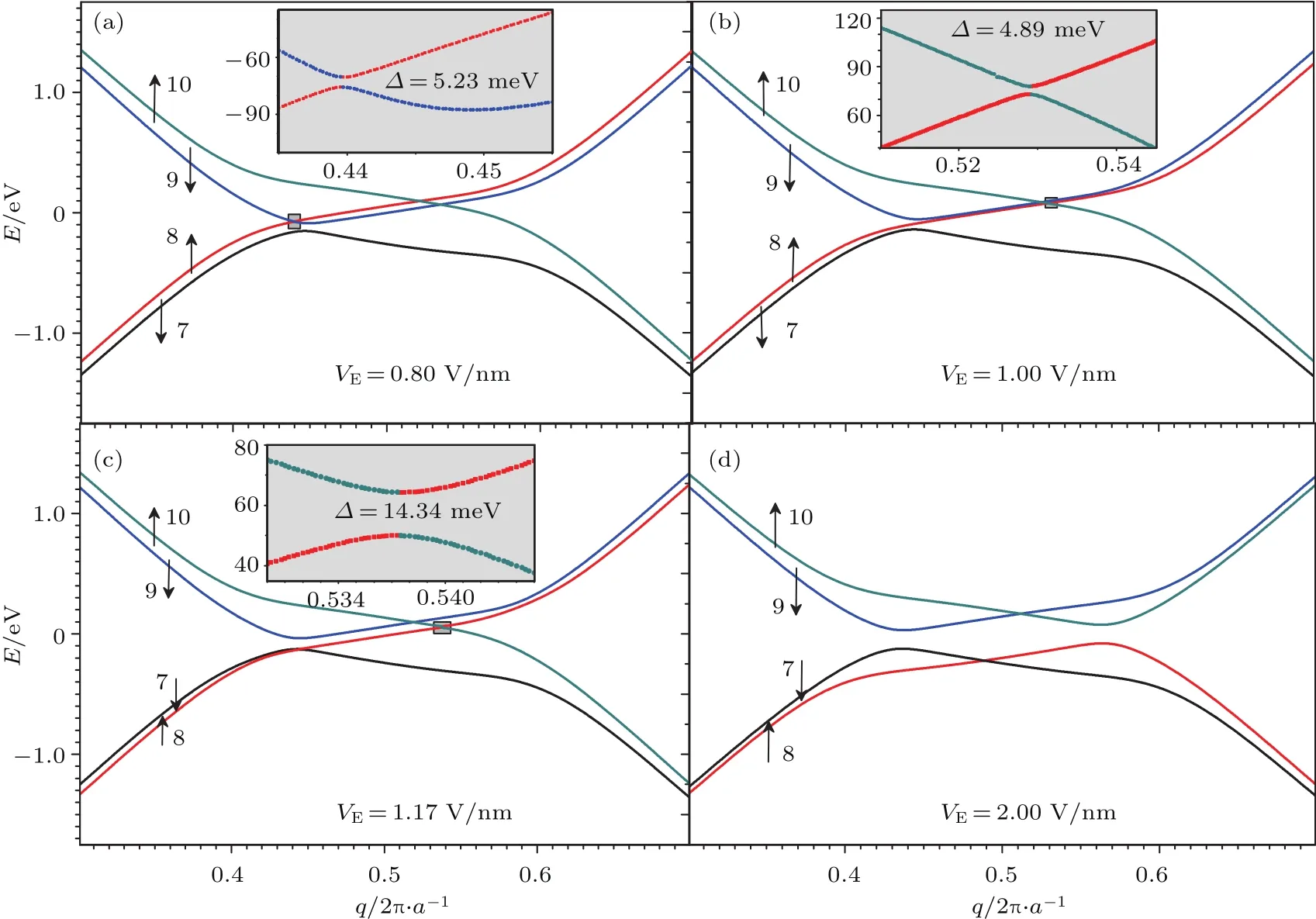
图3 不同电场强度值下石墨烯纳米带4个边界带的能带结构 (a)V E=0.80 V/nm;(b)V E=1.00 V/nm;(c)V E=1.17 V/nm;(d)V E=2.00 V/nm;图中的整数是带指标,箭头代表各带的自旋方向Fig.3.The band structures of four edge bands in the narrow ZGNR under the diff erent strength of the applied electric fi eld:(a)V E=0.80 V/nm;(b)V E=1.00 V/nm;(c)V E=1.17 V/nm;(d)V E=2.00 V/nm.The integers express the band indices,the gray vertical arrows denote the spin directions of bands.

紧接着,研究电场强度对石墨烯纳米带边界带的能带结构的影响.当电场强度逐渐增强时,可以看到4个边界能带中有一个明显变化,自旋向下的7带与9带的交叉点不断向左移动.随电场强度继续增加,7带与9带交叉处的带隙不断增加.为显示4个不同阶段时的能带结构,在图3(a)—(d)中,电场强度分别为0.80,1.00,1.17和2.00 V/nm.当电场强度超过0.69 V/nm时,带隙值达到50 meV,本文中带隙值大于50 meV,即大于室温时热电子能量25 meV的2倍,我们认为7带与9带不能交叉穿越带隙,即能带发生反转,见图3(a);当电场强度超过0.93 V/nm时,自旋向下的导带9带能量值越过了穿过费米能的8带,见图3(b);而当电场强度继续增强,超过1.17 V/nm时,自旋向下的价带7带越过费米能以下的8带,见图3(c);当电场强度大于1.42 V/nm后,8带与10带的带隙值大于50 meV,8带与10带不能交叉穿越带隙,即能带反转,10带成为自旋向上导带,8带成为自旋向上的价带,见图3(d)所示.

下面具体分析讨论上述不同电场强度范围内的4种能带结构图.外电场0.80 V/nm时,如图3(a)所示,7带与9带的带隙为64.21 meV,大于50 meV,因此7带与9带的走向不同于图2(b),能带反转,7带不再与10带交叉,而是9带与10带交叉,7带成为动量空间中一个完整的不与任何带交叉及连接的独立价带;虽然9带与10带和8带交叉,但是在整个动量空间中9带也是独立的导带.显然,此时自旋向下的电子结构能带存在能隙,而自旋向上的电子是无能隙的,系统呈现对自旋向上电子导电,而自旋向下电子禁止的半金属性,这结果也正如Son等[16]理论预言的结论一致.因为自旋向下的7带和9带在整个动量空间是独立的导带和价带,自旋向下电子的量子自旋霍尔效应消失,不再是文献[18]中的B型量子自旋霍尔体系,而是只有自旋向上电子的量子自旋霍尔效应,但是该效应并不在自旋向下电子的能量禁带区域,如图4中I图所示.

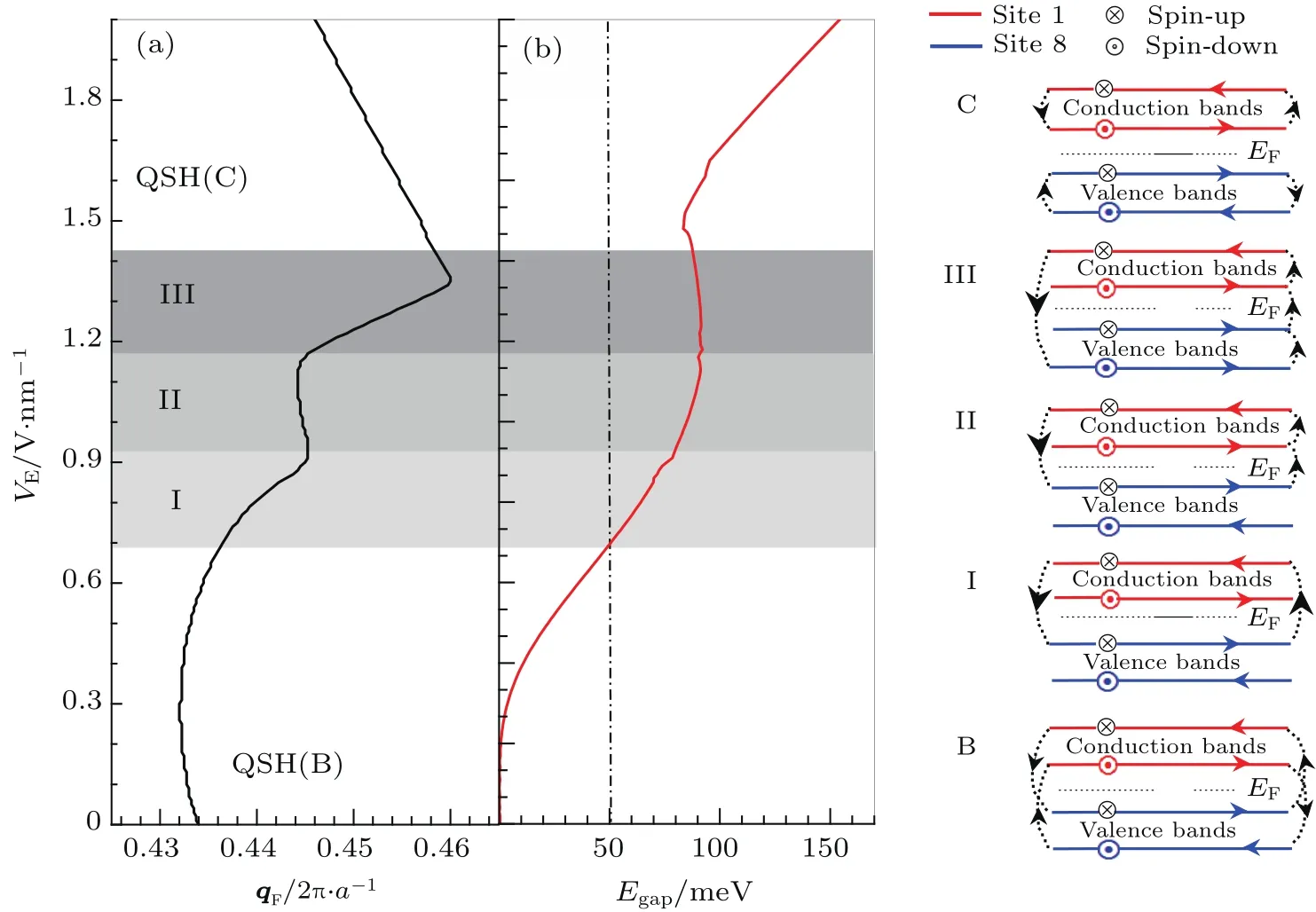
图4 波矢和带隙随电场强度的变化关系 (a)左费米波矢q F(q F单位为2π/a,a为晶格常数)随V E的变化关系;(b)7带与9带的带隙E gap随V E的变化关系,右列为从QSH(B)向QSH(C)过渡中的I,II,III电子态流动示意图;其中为了比较,加入B类和C类电子态流动图;QSH(quantum spin Hall)即量子自旋霍尔Fig.4.The left Fermi wave vector and the gap between band 7 and 9 with increasing strength of the electric fi eld:(a)Left column,the Fermi wave vector with increasing strength of the electric fi eld;(b)middle column:the gap between band 7 and 9 with increasing strength of the electric fi eld;the schematic fl ow diagram of electron state in the right column;there are three processes(I–III)from QSH(B)to QSH(C);the fl ow diagrams of the type B and the type C are for comparison.QSH i.e.quantum spin Hall.

电场强度为1.00 V/nm时,图3(b)中自旋向下的导带9带能量值越过了8带,不再与8带交叉,同时7带与9带的能隙增大为84.98 meV,系统仍然是半金属性的,而且相对于图3(a),在该能隙间隔中的8带电子态在边界格点的占据几率更高,呈现更强的边界态特性,因此,可以预期在自旋向下电子的禁带区域,有纯的自旋向上量子自旋霍尔效应.进一步分析系统量子自旋霍尔体系中的电子态流动图,在整个动量空间,在布里渊区边界处,8带与9带连接,9带与10带连接,所以与图4中I图不同的是,原8带到10带的电子态流动变成8带流向9带和9带流向10带两部分,见图4中II图.

当电场强度为1.17 V/nm时,与图3(b)相比,自旋向下7带的能量越过8带,7带顶与9带底所在波矢q位于0.445,带隙增加为91.04 meV,但是此时8带与10带在q=0.538处的带隙仅为14.34 meV,仍然小于50 meV,自旋向上的8带和10带交叉穿过带隙,自旋向上电子的能带是无能隙的;并且在q=0.5处100%位于边界格点8的自旋向上边界态正好处于自旋向下电子的禁带区域,因此在此区域导电电子是完全沿边界格点8的自旋向上电子,具有最纯的单一自旋向上电子的高效量子霍尔效应.进一步分析此时系统的量子自旋霍尔体系中的电子态流动图,显然,由于边界7带越过了8带导致电子态流动发生了变化,此时自旋向下的7带不再是一个独立的价带,在布里渊区的边界处,7带与8带连接,8带与9带连接,9带与10带连接,电子态流动图如图4中III图所示.

当电场继续增强,边界8带与10带之间的带隙越来越大.当电场强度为2.00 V/nm时,在q=0.563处带隙达到154.55 meV,大于50 meV,此时自旋向上的8带与10带不能交叉穿过,因此自旋向上电子的能带结构不同于图3(a)—(c),10带成为导带,8带成为价带.故此带隙成为自旋向上电子能带结构中的能隙,能带结构如图3(d)所示,而自旋向上的7带与9带在q=0.437处能隙也达到154.32 meV,此时系统不再是半金属性的.处于边界格点1上自旋向下9带与自旋向上10带构成导带,而处于边界格点8上自旋向下7带与自旋向上8带构成价带.分析电子态的流动,在布里渊区的边界处,导带和价带内的带各自连接形成流动,在禁带区域没有电子流动,见图4中C图,体系完全成为C类[18]量子自旋霍尔体系.

4 总 结

通过对锯齿型石墨烯纳米窄带平面内加入横向电场,在自洽格点在位库仑能的基础上,用电场控制空间各格点上电子的电势能分布.研究结果显示,可以用电场调控4个边界带的能带结构,控制自旋电流,改变系统的量子自旋霍尔体系.当电场强度较弱时,外加电场的方向不同,在q=0.5处自旋向下的处于不同边界格点的两个边界带朝不同能量方向分开,因此,在高(或低)能量处,可以通过调控电场方向,产生不同方向的纯自旋电流,并且调控自旋向下的电流在不同边界处出现.随着电场强度的增强,平面内横向电场确实可以使系统从量子自旋霍尔体系B类变为C类,这个过程中经历了3个不同的量子自旋霍尔体系.特别是当电场强度介于1.17—1.42 V/nm时,在q=0.5处100%位于边界格点8的自旋向上边界态正好处于自旋向下电子的禁带区域,导电电子是完全沿边界格点8的自旋向上的电子,具有纯自旋向上的边界电流.

[1]Novoselov K S,Geim A K,Morozov SV,Jiang D,Zhang Y,Dubonos S V,Grigorieva I V,Firsov A A 2004 Science 306 666

[2]Novoselov K S,Geim A K,Morozov S V,Jiang D,Katsnelson M I,Grigorieva I V,Dubonos S V,Firsov A A 2005 Nature 438 197

[3]Wallace P R 1947 Phys.Rev.71 622

[4]Neto A H C,Guinea F,Peres N M R,Novoselov K S,Geim A K 2009 Rev.Mod.Phys.81 109

[5]Fujita M,Wakabayashi K,Nakada K,Kusakabe K 1996 J.Phys.Soc.Jpn.65 1920

[6]Kane C L,Mele E J 2005 Phys.Rev.Lett.95 226801

[7]Kane C L,Mele E J 2005 Phys.Rev.Lett.95 146802

[8]Dresselhaus G F,Dresselhaus M S,Mavroides J G 1966 Carbon 4 433

[9]Min H,Hill J E,Sinitsyn N A,Sahu B R,Kleinman L,MacDonald A H 2006 Phys.Rev.B 74 165310

[10]Qiao Z,Wang J 2007 Nanotechnology 18 435402

[11]Zarea M,Sandler N 2009 Phys.Rev.B.79 165442

[12]Zarea M,Sandler N 2009 Phys.B:Condens.Matter 404 2694

[13]Hatsugai Y 1993 Phys.Rev.Lett.71 3697

[14]Xu X Z,Yu J C,Zhang Z H,Liu K H 2017 Chin.Sci.Bull.62 2220(in Chinese)[徐小志,余佳晨,张智宏,刘开辉2017科学通报62 2220]

[15]Zhang Y B,Tang T T,Girit C,Hao Z,Martin M C,Zettl A,Crommie M F,Shen Y R,Wang F 2009 Nature 459 820

[16]Son Y W,Cohen M L,Louie S G 2006 Nature 444 347

[17]Wang Z G,Hao N N,Zhang P 2009 Phys.Rev.B 80 115420

[18]Li H C,Sheng L,Xing D Y 2012 Phys.Rev.Lett.108 196806

[19]Guo J,Gunlycke D,White C T 2008 Appl.Phys.Lett.92 163109

[20]Gunlycke D,Areshkin D A,Li J,Mintmire J W,White C T 2007 Nano Lett.7 3608

[21]Hu B,Liu N,Liu H 2018 Journal of Nanjing Normal University 41 42[胡边,刘娜,刘红2018南京师范大学学报41 42]

[22]Liu H,Hu B,Liu N 2016 Phys.Lett.A 380 3738

[23]Sheng L,Sheng D N,Ting C S,Haldane F D M 2005 Phys.Rev.Lett.95 136602