Korteweg-de Vries方程的准孤∗立子解及其在离子声波中的应用
王建勇 程雪苹 曾莹 张元祥 葛宁怡
1)(衢州学院教师教育学院,衢州 324000)
2)(浙江海洋大学物理系,舟山 316004)
3)(衢州学院机械工程学院,衢州 324000)
(2017年12月18日收到;2018年1月28日收到修改稿)
1 引 言
Korteweg-de Vries(Kd V)方程是孤子理论的基础模型之一,它具有非常典型的可积性,如Lax表示[1]、无穷多对称及守恒律[2]、N-孤子解[3]及Painlevé性质[4]等.KdV方程也是物理学诸多分支学科中一个重要的非线性数学物理模型,在非线性光学、玻色-爱因斯坦凝聚、等离子体物理、生物物理等分支学科中都有着广泛的应用[5].在等离子体物理中,Kd V方程可描述有限小振幅离子声波、磁声波、阿尔文波[6]等.例如,在近期的一项实验研究报告中,Bandyopadhyay等[7]指出尘埃声孤立波的振幅和特征宽度随等离子体参数的变化可由KdV方程的经典孤立子解来描述,而在有限小振幅及低马赫数条件下,理论结果更是和实验数据高度符合.
孤子方程的解析解研究是非线性科学中的热点课题[8,9].最近,通过非局域对称的局域化及对称约化,Lou等[10]给出了Kd V方程、非线性Schrödinger方程等若干孤子方程的孤子-椭圆周期波解,并发现孤子和椭圆周期波之间的相互作用是弹性的,相互作用后两者仅有相位变化.基于这些方法,Lou[11]又提出了推广的Painlevé截断展开法和推广的tanh函数展开法.应用此类推广的方法可直接给出孤子与其他非线性波的相互作用解,如孤子与椭圆周期波、Painlevé波、Airy波、Bessel波等的相互作用解[12−20].而在等离子体物理中,人们很早就开始了关于孤子与小振幅周期波之间相互作用的数值研究[21,22].例如,Deeskow等[21]早在1987年就应用数值方法研究了非磁化等离子体中离子声波和朗缪尔波同时激发的情况,在允许离子扰动和电荷分离条件下,朗缪尔波电场和离子声波电势的耦合是一种具有准孤子行为的结构,即朗缪尔波电场可由包络孤子描述,而离子声波电势则以小振幅周期波的形式围绕在包络孤子周围.最近,Keane等[22]也进行了这方面的研究,从包含量子修正的霍尔磁流体力学方程组出发,导出了耦合Zakharov型方程并进行了数值研究,发现初值解形如穿了“衣服”的孤立波,即高斯波峰被小振幅周期波围绕,并具有在时空演化中保持波形不变的性质.此外,流体力学中已有关于孤立波和小振幅周期波之间相互作用的实验研究和实际观测[23−25].例如,Farmer和Smith[24]以及Akylas和Grimshaw[25]曾在加拿大某海湾观测到了类似孤立波的结构与小振幅周期波之间的相互作用现象.
本文考虑Kd V方程的孤子-椭圆周期波解及其准孤立子行为.应用推广的tanh函数展开法,给出Kd V方程具有准孤立子行为的两组孤子-椭圆周期波解及双孤立子解.另外,运用约化摄动法推导描述离子声波动力学行为的KdV方程,并由此讨论等离子体参数对离子声准孤立子波形的影响.
2 Kd V方程的准孤立子解
在等离子体物理中,Kd V方程一般可写为
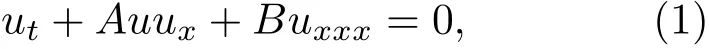
其中A是非线性项系数,B是色散项系数,两者由等离子体参数决定.根据推广的tanh函数展开法,可知KdV方程的解u具有如下截断展开[14]:
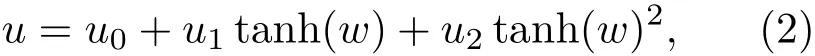
其中ui和w都是关于(x,t)的待定函数.将截断展开(2)式代入Kd V方程,并令tanh(w)5,tanh(w)4,tanh(w)3的系数为零,可求得u2,u1及u0为:
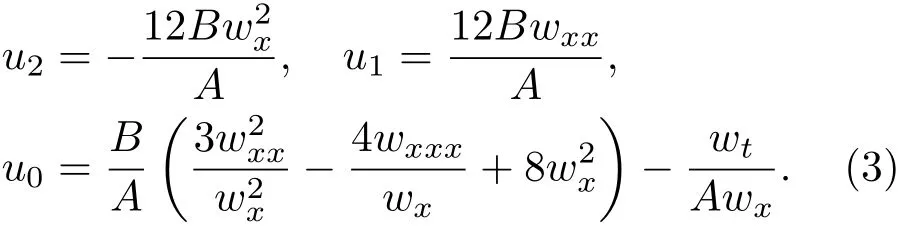
将(3)式代入tanh(w)2的系数方程,可得w的相容性方程
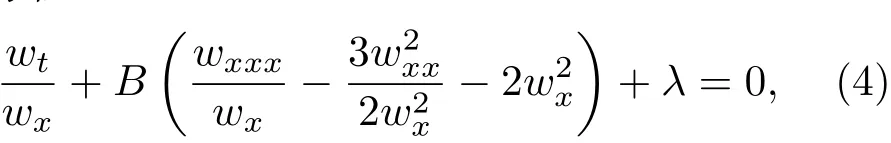
其中λ是积分常数.由(3)式和(4)式,Kd V方程的解(2)可写为
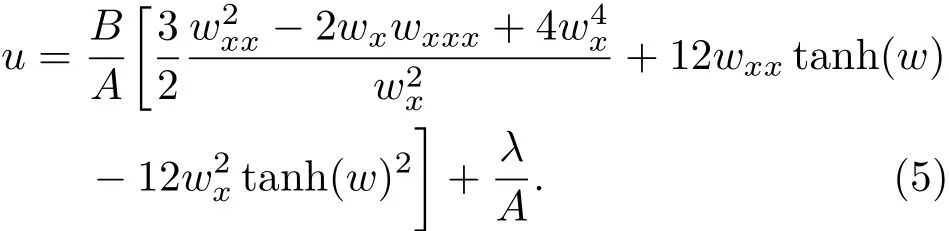
最后,可直接验证(3)式—(5)式满足tanh(w)1和tanh(w)0的系数方程.由此说明,若w满足其相容性方程(4),则(5)式为Kd V方程的解.
为了求得Kd V方程的孤子-椭圆周期波解,可将w设为[26]:
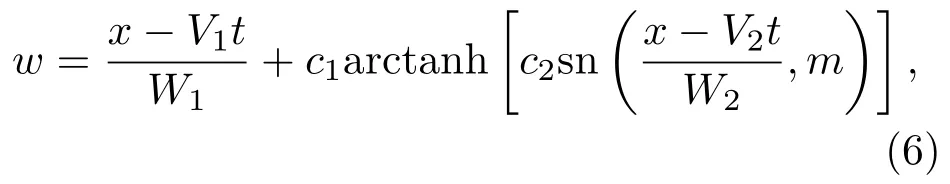
其中sn是Jacobi椭圆正弦函数,m为其模数,V1,V2分别为孤立波和椭圆周期波的速度,W1是孤立波的特征宽度,W2与椭圆周期波波长相关.将关于w的假设(6)式代入相容性方程(4),由Jacobi椭圆函数sn,cn,dn的各阶系数可得到关于参数{m,V1,V2,W1,W2,c1,c2,λ}的超定方程组.在这些超定方程组中,若取{m,V1,V2}为任意值,则可求得关于{W1,W2,c1,c2,λ}的参数解.在较早的研究中[26],给出了其中一组参数解:
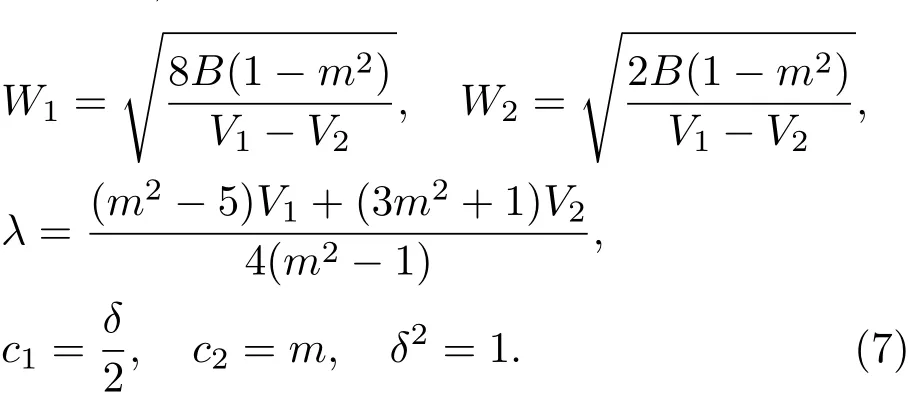
在此参数条件下,Kd V方程的孤子-椭圆周期波解具有比较简洁的形式:
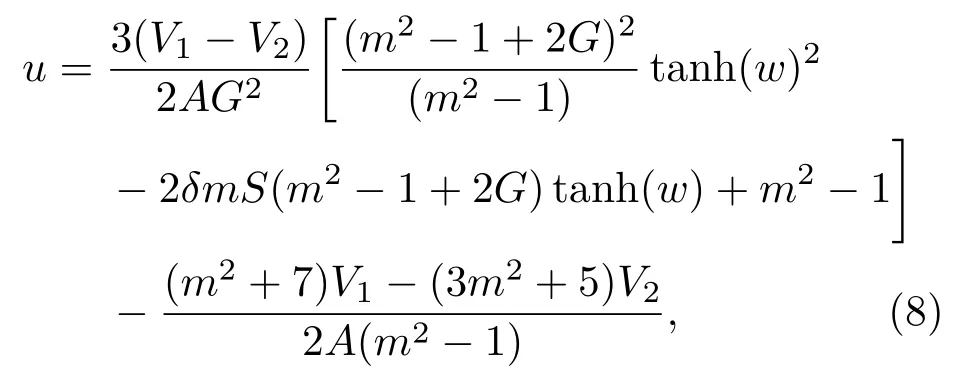
其中
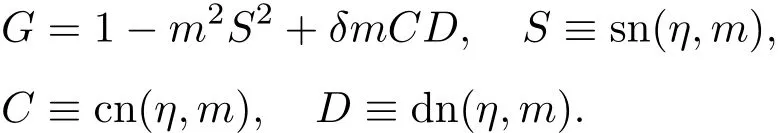
在孤子-椭圆周期波解(8)中,取V1=V,V2=−V及m=0可得满足零边界条件的经典孤立子解为:
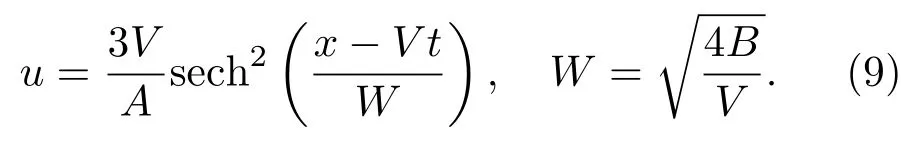
由此不难发现孤子-椭圆周期波解(8)在渐进条件V1=V,V2=−V及m→0下具有准孤立子行为.
研究发现孤子-椭圆周期波解的参数条件也可取为:
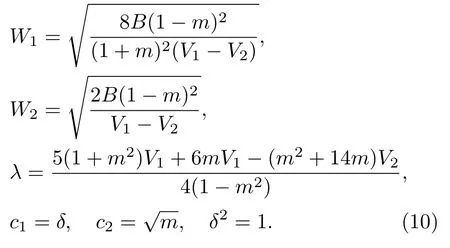
由此参数条件,可得KdV方程的一个新孤子-椭圆周期波解,其形式略为复杂:
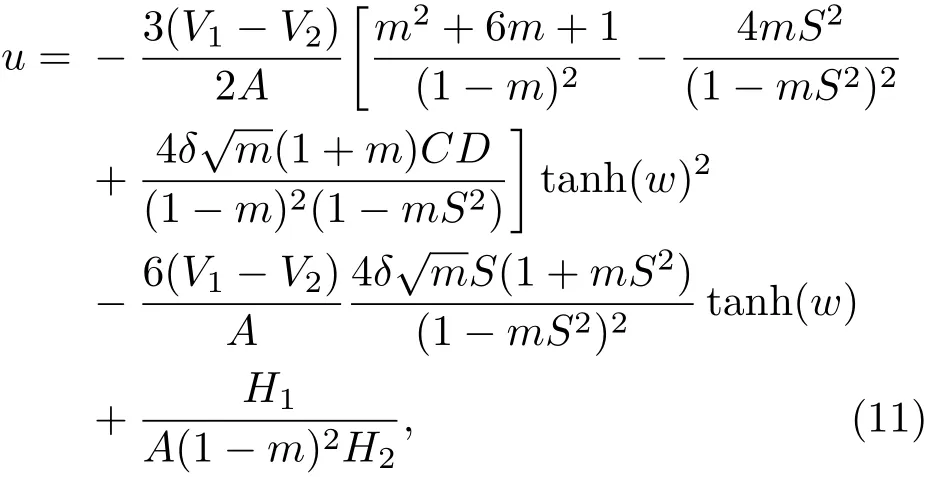
其中H1和H2的具体表达式见附录A.孤子-椭圆周期波解(11)在渐进条件V1=V,V2= −V及m → 0下也具有准孤立子行为,下面以图示说明.准孤立子解(11)与经典孤立子解(9)的对比如图1所示,由m=0.0016,m=0.0004及经典孤立子解(m=0)的波形对比可知,m取值越小,孤子-椭圆周期波解的孤子核越接近于满足零边界条件的经典孤立子,而围绕在其周围的椭圆周期波也越接近于在零附近振荡的正余弦波.Kd V方程的孤子-椭圆周期波解(8)式和(11)式都具有准孤立子行为,可统称为准孤立子解.
显然,在参数条件(7)式和(10)式中,m都不可取为1.因此,孤子-椭圆周期波解(8)和(11)式都无双孤立子极限.为求得双孤立子解,可将w设为:
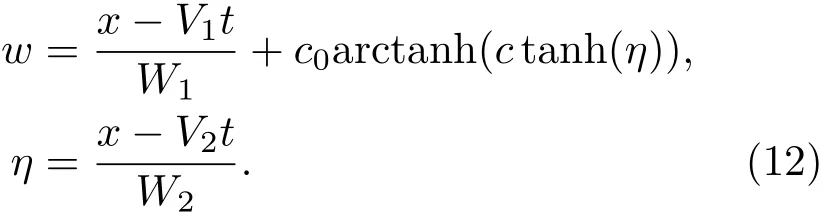
将(12)式代入相容性方程(4),令tanh(η)的各阶系数为零,可求得关于{c0,W1,W2,λ}的参数解:
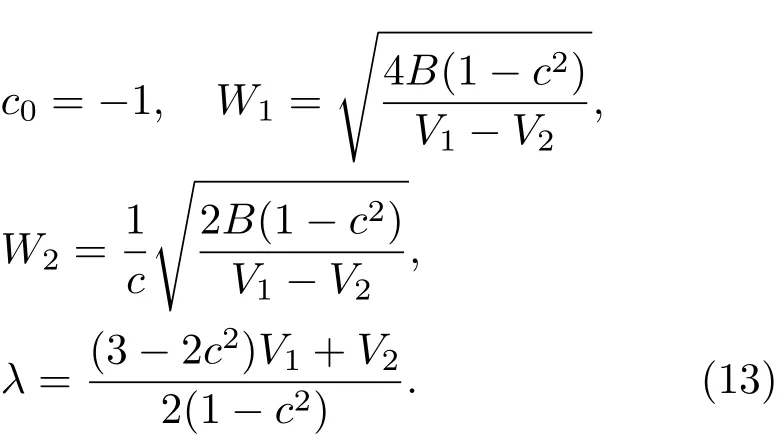
由(5)式,(12)式及(13)式,可给出KdV方程的双孤立子解:
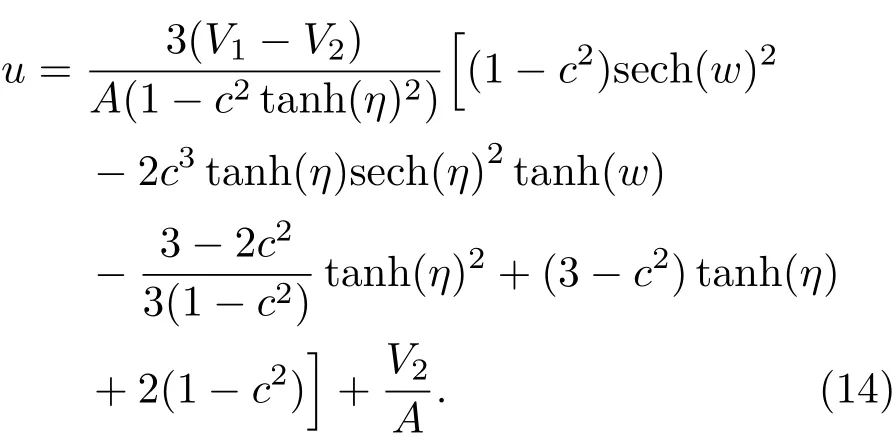
图2是由(14)式描述的双孤立子追赶相互作用,其中高瘦孤立波的波速为V1=1.25,矮胖孤立波的波速为V2=0.75.由图2可知,两孤立波在发生追赶相互作用后并不改变原有的波形与波速,仅发生相位变化.
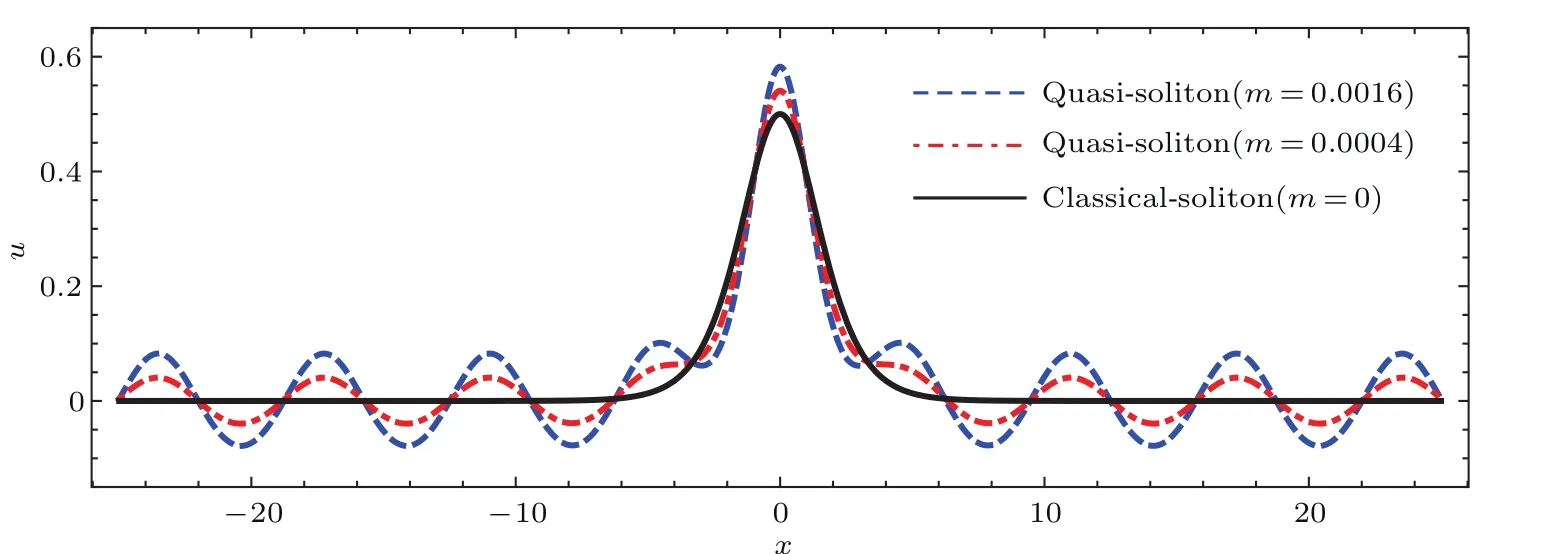
图1 准孤立子解(11)与经典孤立子解(9)的对比 波参数为V1=1,V2=−1,V=1及δ=1,Kd V方程的系数为A=6,B=1Fig.1.Comparison of quasi-soliton solution(11)with the classical solion solution(9).Wave parameters are selected as V1=1,V2=−1,V=1,δ=1 and coeffi cients of the Kd V eqation are A=6,B=1.
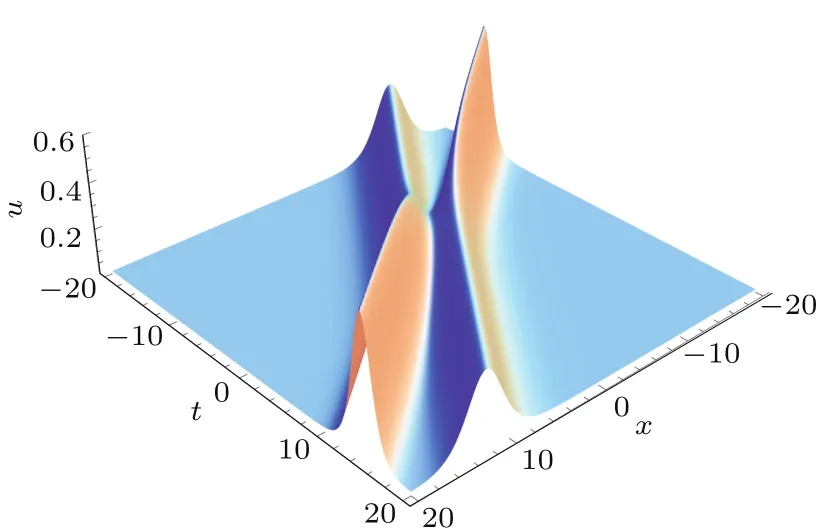
图2 由(14)式给出的双孤立子相互作用 波参数为V1=1.25,V2=0.75及c=0.75,Kd V方程的系数为A=6,B=1Fig.2.Two soliton interaction given by equation(14).Wave parameters are selected as V1=1.25,V2=0.75,c=0.75 and coeffi cients of the Kd V eqation are A=6,B=1.
3 描述离子声波动力学行为的KdV方程
考虑均匀磁化等离子中的离子声波,等离子体的成分是超热电子和热离子.相对于离子,电子质量极小,可忽略电子惯性.假设等离子体沉浸在恒定磁场B=B0ˆz中,ˆz是单位矢量.平衡态时,由电中性可知ne0=ni0=n0,ne0,ni0分别是平衡态时的电子、离子数密度.另外,假设超热电子遵循κ分布
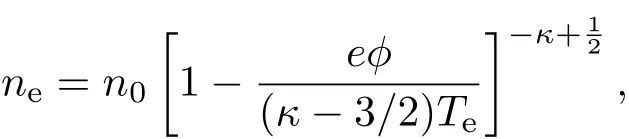
其中,参数κ(κ>3/2)是表征电子分布偏离麦克斯韦分布程度的物理量.
在上述条件下,离子声波的动力学行为可由连续性方程、动量方程和泊松方程来描述:
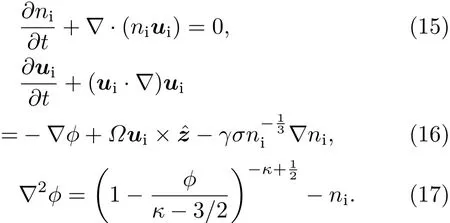
(15)式—(17)式中,ni是热离子的粒子数密度,由平衡态离子数密度n0无量纲化;ui是由离子声速Cs=(Te/mi)(1/2)无量纲化后的离子流体速度;电势ϕ则由Te/e无量纲化;时间变量和空间变量分别经离子等离子体离子频率的倒数 ωp−i1=和德拜长度无量纲化;离子回旋频率经离子等离子体频率ωpi无量纲化;σ=Ti/Te是离子电子温度比.对于低频离子声波过程,可认为电子是绝热的,动量方程(16)式中的绝热系数可取为γ=5/3.此外,对于有限小振幅波≪1,泊松方程可做如下近似展开:
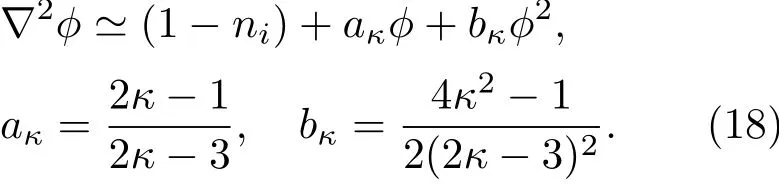
下面应用约化摄动法来研究磁化超热电子-热离子中的有限小振幅离子声波.首先引入坐标变换
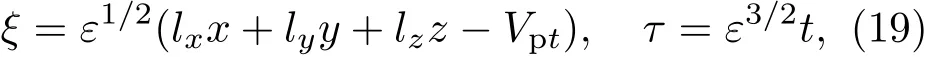
其中ε≪1是描述弱色散效应的无穷小参数,Vp是待定离子声波相速度;lx,ly,lz是波矢量k沿x,y,z方向的余弦值,且lx,ly,lz满足l2x+l2y+l2z=1.由于磁场在各个方向的非均匀性,相对于平行于磁场方向的离子流体速度分量,离子流体速度沿垂直于磁场方向的分量应在ε的更高阶次.故可将独立变量在平衡态附近按ε的幂次展开为:
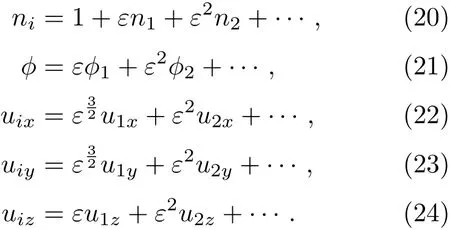
将(20)式—(24)式代入流体力学方程组(15)式—(17)式并收集ε的各阶系数,可得到关于各阶扰动量的相容性方程.由ε的最低幂次,可求得n1,u1x,u1y及u1z为
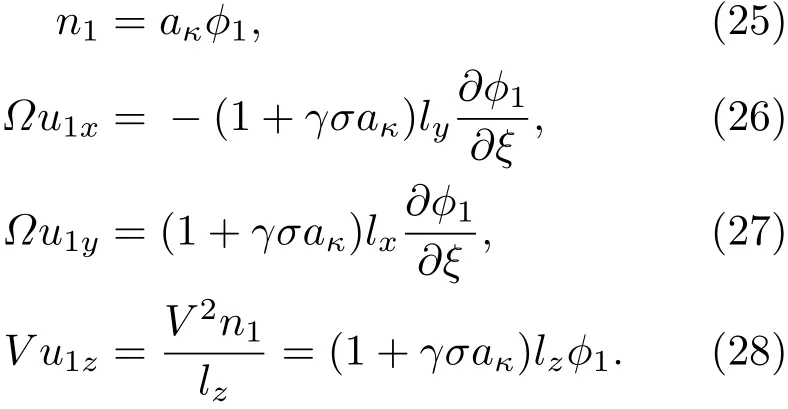
由(25)式—(28)式可给出离子声波的相速度Vp为
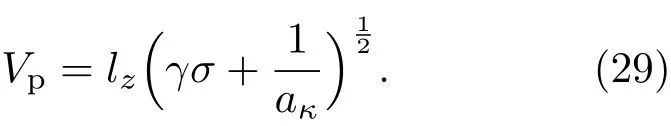
由(29)式可知,当离子电子温度比σ增加时,离子声波相速度增加;当磁场方向与波矢量方向的夹角增加时(lz减小),离子声波相速度减小;当电子偏离麦克斯韦分布的程度增加时(κ减小),aκ增大,离子声波相速度减小.
由ε的高一阶幂次的系数,可得关于二阶小量的相容性方程.代入(25)式—(29)式可求得:
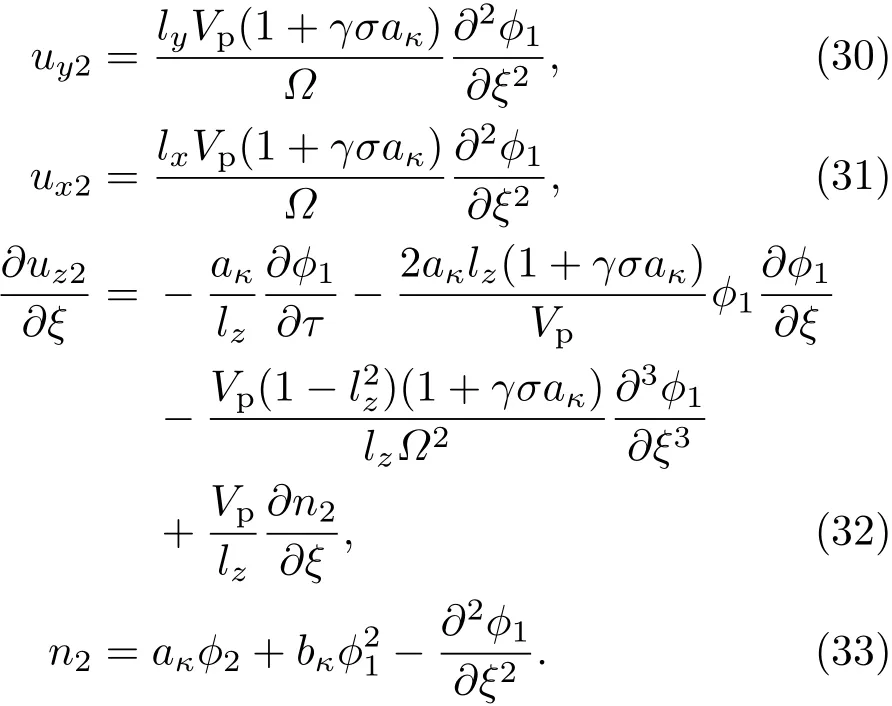
由(30)式—(33)式的相容性,可给出KdV方程
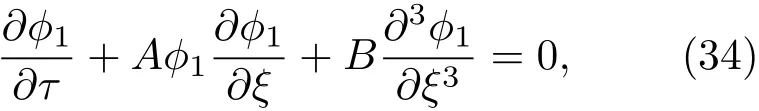
其中,非线性项系数A和色散项系数B为:
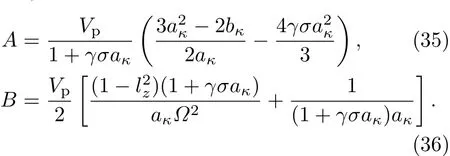
4 等离子体参数对波形的影响
由于Kd V方程的非线性项系数A和色散项系数B由等离子体物理参数决定,故等离子体参数的变化会引起孤子核的特征宽度和振幅的变化,同样也会引起围绕在其周围的小振幅周期波的波长和振幅的变化.下面讨论在实验室坐标系中等离子体参数对离子声准孤立子波形的影响.在(21)式中,忽略高阶小量,可取ϕ=εϕ1.由(8)式及(19)式,不难给出电势离子声准孤立子在实验室坐标系下的表达式.
首先,考虑电子分布偏离麦克斯韦分布的程度(κ)对离子声准孤立子波形的影响.对于遵循κ分布的电子,当κ减小时,超热电子成分增加,电子偏离麦克斯韦分布的程度增加;当κ增大时,超热电子成分减少,电子偏离麦克斯韦分布的程度减小.图3为离子声准孤立子波形随电子分布偏离麦克斯韦分布程度(参数κ)的变化,由图可知,当κ增大时,即电子分布偏离麦克斯韦分布的程度减小时,孤子核的振幅和特征宽度都增大,围绕在孤子核周围的小振幅周期波的振幅和波长也都增大.当κ→∞时,电子遵循麦克斯韦分布,孤子核的振幅和特征宽度、小振幅周期波的振幅和波长达到最大值.这种现象说明,当超热电子变得越来越稀疏时(κ增大),Kd V方程的非线性项系数A减小而色散项系数B增大,进而使孤子核的振幅和特征宽度、小振幅周期波的振幅和波长都增大.从物理上来讲,离子声波由电子热压强提供驱动力,而κ增大的过程也可视为电子热压强增加的过程,从而使孤子核的振幅和特征宽度、小振幅周期波的振幅和波长都增大.文献[27]研究了电子分布参数κ对经典孤立子波形的影响,研究表明κ增大将导致经典孤立子的振幅和特征宽度都增大;而当κ→∞时,经典孤立子的振幅和特征宽度达到最大值,其研究结果与本文一致.
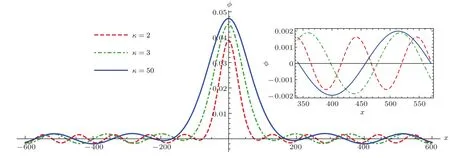
图3 离子声准孤立子波形随电子分布偏离麦克斯韦分布程度(参数κ)的变化 波参数为ε=0.1,m=0.02,δ=−1,V1= −V2=0.05,Ω =0.3,σ=0.01,l x=0.5及l z=0.3Fig.3.Variation of the ion acoustic(IA)quasi-soliton structure with respect to the electron superthermalityκ.Wave parameters areε=0.1,m=0.02,δ=−1,V1=−V2=0.05,Ω =0.3,σ=0.01,l x=0.5 and l z=0.3.
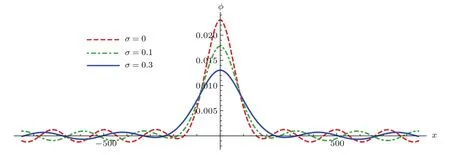
图4 离子声准孤立子波形随离子与电子之间温度比σ=T i/T e的变化 波参数为ε=0.05,m=0.025,δ=−1,V1=−V2=0.05,l x=0.5,l z=0.3,Ω=0.3及κ=3Fig.4.Variation of the IA quasi-soliton structure with respect to the ion to electron temperature ratioσforε=0.05,m=0.025,δ=−1,V1=−V2=0.04,l x=0.5,l z=0.3,Ω =0.3 andκ=3.
其次,考虑离子电子温度比(σ)对离子声准孤立子波形的影响.图4为离子声准孤立子波形随离子与电子之间温度比σ=Ti/Te的变化,由图可知,当离子与电子之间温度比σ=Ti/Te减小时,孤子核振幅、周期波振幅增大,孤子核特征宽度、周期波波长减小;当离子为冷离子,即σ=0时,孤子核振幅、周期波振幅达到最大值,而孤子核特征宽度、周期波波长达到最小值.这种现象说明,当离子与电子之间温度比σ减小时,Kd V方程的非线性项系数A和色散项系数B都减小,进而使孤子核振幅、周期波振幅增大,孤子核特征宽度、周期波波长减小.文献[28]研究了离子与电子之间温度比对经典孤立子的影响,发现离子电子温度比σ=Ti/Te减小时,经典孤立子的振幅将增大而特征宽度将减小,此结果与图4孤子核的波形变化一致.
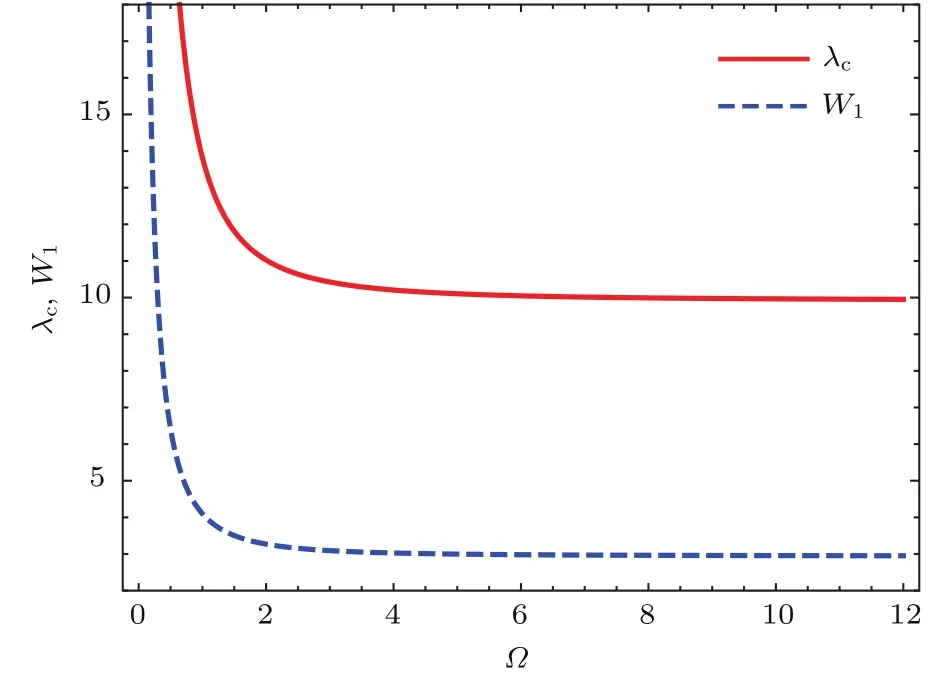
图5 孤子特征宽度及周期波波长随磁场大小Ω的变化波参数为m=0.02,δ=1,V1=−V2=0.05;等离子体参数为σ=0.01,l z=0.3及κ=50Fig.5.Variation of soliton width and wavelength of periodic wave with respect to the electron magnetic fi eld strengthΩ for m=0.02,δ=1,V1=−V2=0.05 and plasma parameters areσ=0.01,l z=0.3 and κ=50.
第三,考虑离子声准孤立子波形随磁场大小Ω的变化.由(35)和(36)式可知,非线性项系数A与磁场大小Ω无关,因此,孤子核振幅、周期波振幅与磁场大小Ω变化无关.下面仅讨论磁场大小Ω对孤子核特征宽度、周期波波长的影响.(7)式给出了孤子核特征宽度表达式,文献[26]由“穿衣服”结构给出了周期波波长为λc=4K(m)W2,K(m)是第一类Legendre完全椭圆积分,由此可做图讨论.图5为孤子特征宽度及周期波波长随磁场大小Ω的变化,由图可知,当磁场取值较小时,Ω增大将导致孤子核特征宽度、周期波波长显著减小.当Ω进一步增大时,孤子核特征宽度、周期波波长都将趋向一固定值.此现象可由KdV方程色散项系数的表达式给出解释.当磁场大小Ω达到极限,即(1−l2z)(γσ+1/aκ)≪ Ω2时,色散项系数B可近似取为
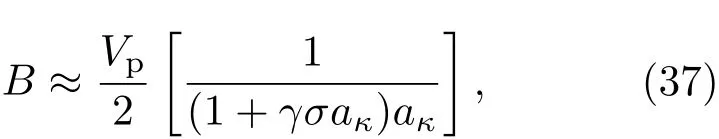
此时,色散项系数B与Ω无关,故孤子核特征宽度、周期波波长存在极限值.文献[27,29]考虑了磁场大小Ω对经典孤立子的影响,也发现磁场大小Ω对孤子特征宽度的影响存在一个极限值.
最后,讨论离子声准孤立子波形随磁场方向与波矢量之间夹角的变化.图6为离子声准孤立子波形随倾斜程度lz的变化,由图可知,当磁场B与波矢量k之间夹角θ增大时,lz减小,孤子核振幅、周期波振幅增大,孤子核特征宽度、周期波波长减小.当磁场B与波矢量k之间夹角为直角时,lz为零,孤子核振幅、周期波振幅达到最大值,孤子核特征宽度、周期波波长达到最小值.
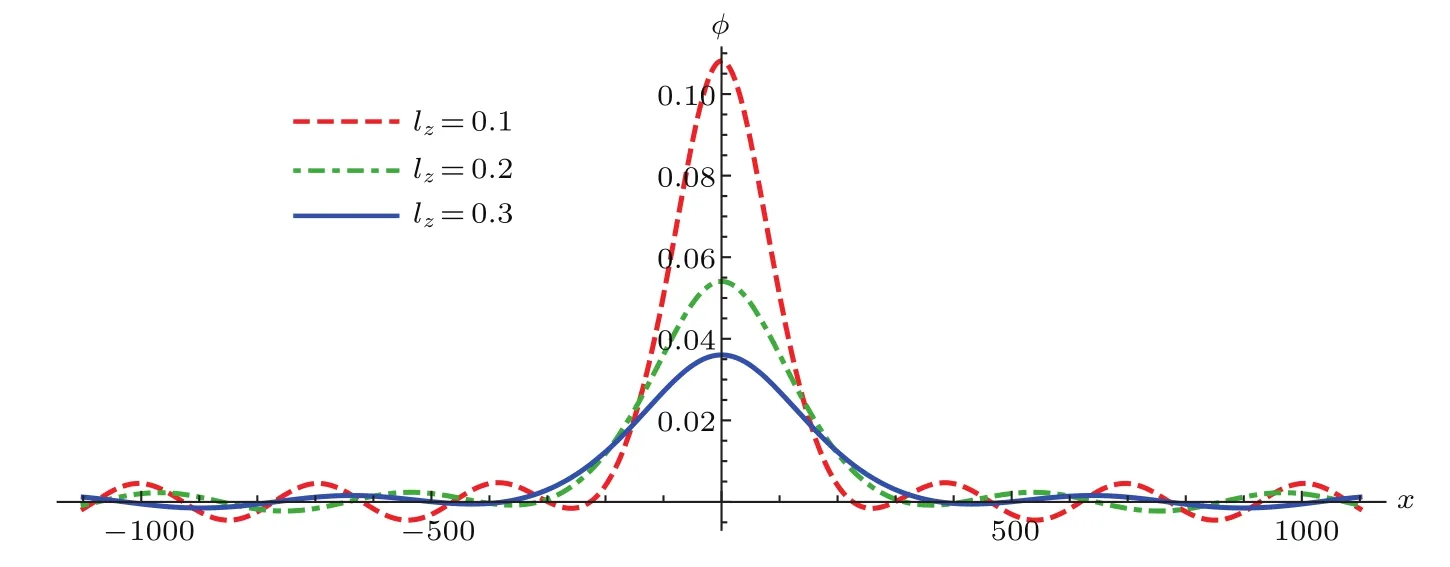
图6 离子声准孤立子波形随倾斜程度l z的变化 波参数为ε=0.1,m=0.02,δ=−1,V1=−V2=0.04,l x=0.5,Ω=0.3,σ=0.01及κ=3Fig.6.Variation of the IA quasi-soliton structure with respect to obliqueness l z forε=0.1,m=0.02,δ=−1,V1=−V2=0.04,l x=0.5,Ω =0.3,σ=0.01 andκ=3.
5 结 论
本文应用推广的tanh函数展开法给出了KdV方程具有准孤立子行为的两组孤子-椭圆周期波解,其中一组为新解.讨论了均匀磁化等离子体中描述离子声波动力学行为的准孤立子,发现电子分布偏离麦氏分布、离子电子温度比、磁场大小和磁场方向对离子声准孤立子波形具有显著影响.本文给出的准孤立子解可应用到物理学的众多领域.例如,可将准孤立子解视为“穿衣服”孤立子,并在实验和数值研究中给出经典孤立子解的修正.
附录A
H1和H2的具体表达式为:
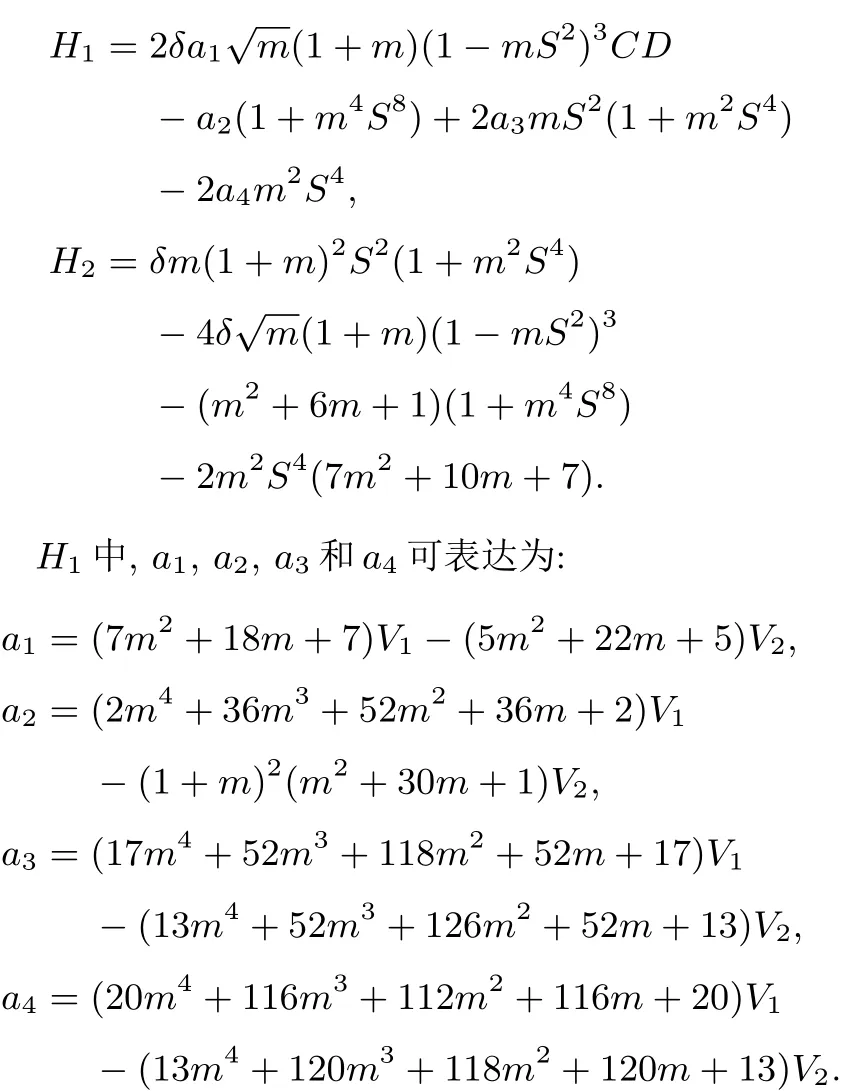
[1]Lax P D 1968 Commun.Pur.Appl.Math.21 467
[2]Miura R,Gardner C,Kruskal M 1968 J.Math.Phys.9 1204
[3]Hirota R 1971 Phys.Rev.Lett.27 1192
[4]Weiss J,Tabor M,Carnevale G 1983 J.Math.Phys.25 522
[5]Dauxois T,Peyrard M 2006 Physics of Solitons(Cambridge:Cambridge University Press)
[6]Jeff rey A,Kakutani T 1972 SIAM Rev.14 582
[7]Bandyopadhyay P,Prasad G,Sen A,Kaw P K 2008 Phys.Rev.Lett.101 065006
[8]Cheng X P,Li J Y,Xue J R 2011 Acta Phys.Sin.60 110204(in Chinese)[程雪苹,李金玉,薛江蓉2011物理学报60 110204]
[9]Mao J J,Yang J R,Li C Y 2012 Acta Phys.Sin.61 020206(in Chinese)[毛杰健,杨建荣,李超英2012物理学报61 020206]
[10]Lou SY,Hu X R,Chen Y 2012 J.Phys.A:Math.Theor.45 155209
[11]Lou S Y 2015 Stud.Appl.Math.134 372
[12]Tang X Y,Hao X Z,Liang Z F 2017 Comp.Math.Appl.74 1311
[13]Tang X Y,Liang Z F,Wang J Y 2015 J.Phys.A:Math.Theor.48 285204
[14]Gao X N,Lou S Y,Tang X Y 2013 JHEP 05 029
[15]Chen C L,Lou S Y 2013 Chin.Phys.Lett.30 110202
[16]Cheng X P,Lou S Y,Chen C L,Tang X Y 2014 Phys.Rev.E 89 043202
[17]Ren B,Cheng X P,Lin J 2016 Nonlinear Dyn.86 1855
[18]Ren B 2017 Commun.Nonlinear Sci.Numer.Simul.42 456
[19]Hao X Z,Liu Y P,Tang X Y,Li Z B 2016 Comp.Math.Appl.72 2405
[20]Wang J Y,Cheng X P,Tang X Y,Yang J R,Ren B 2014 Phys.Plasmas 21 032111
[21]Deeskow P,Schamel H,Rao N N,Yu M Y,Varma R K,Shukla P K 1987 Phys.Fluids 30 2703
[22]Keane A J,Mushtaq A,Wheatland M S 2011 Phys.Rev.E 83 066407
[23]Davis R E,Acrivos A 1967 J.Fluid Mech.29 593
[24]Farmer D M,Smith J D 1980 Deep-sea Rea.27A 239
[25]Akylas T R,Grimshaw R H J 1992 J.Fluid Mech.242 279
[26]Wang J Y,Tang X Y,Lou S Y,Gao X N,Jia M 2014 Europhys.Lett.108 20005
[27]Williams G,Kourakis I 2013 Plasma Phys.Controlled Fusion 55 055005
[28]Singh S V,Devanandhan S,Lakhina G S,Bharuthram R 2013 Phys.Plasmas 20 012306
[29]Saini N S,Kourakis I 2010 Plasma Phys.Controlled Fusion 52 075009

