Tavis-Cummings模型中的几何量子失协特性∗

程景 单传家 刘继兵 黄燕霞 刘堂昆

(湖北师范大学物理与电子科学学院,黄石 435002)

(2017年12月20日收到;2018年3月14日收到修改稿)

1 引 言

量子纠缠是量子力学最基本的概念,是一种量子关联,也是量子物理与经典物理最本质的区别,在量子信息中被广泛地应用,例如量子密钥分配[1]、量子隐形传态[2]、量子纠错[3]和量子网络等.目前人们对Tavis-Cummings(T-C)模型进行了更广泛的研究,Bogoliubov等[4]对加入克尔非线性介质的T-C模型进行了讨论;左战春和夏云杰[5]对T-C模型中三体纠缠态纠缠量进行了讨论;郭亮和梁先庭[6]研究了T-C模型中光场和原子以及原子与原子之间的纠缠演化;张国锋和卜晶晶[7]研究了共振和非共振情况下非简并双光子T-C模型中原子与原子之间的纠缠演化.但是,实验上和理论上证实了量子纠缠不包含所有的量子关联.为更加全面地描述量子关联,Ollivier和Zurek[8]提出了量子失协(quantum discord,QD);胡要花等[9]研究了强度相关耦合双Jaynes-Cummings(J-C)模型中的纠缠和QD;贺志和李龙武[10]研究了两能级原子在共同环境下的量子关联动力学;Ali等[11]发现纠缠与QD并没有直接的大小关系.量子纠缠不完全等同于非经典关联,有的系统即使量子纠缠等于0,但是仍然存在量子失协,所以QD引起了人们浓厚的兴趣.但是仅对于一些特殊的态,才能得到QD的精确解析.为了克服这个问题,Dakic等[12]提出了几何量子失协(geometric measure of quantum discord,GQD)的方法,用此方法解析两体问题相对于QD要简单很多.樊开明和张国锋[13]研究了阻尼J-C模型中两原子的量子关联动力学.对GQD的研究更为广泛[14−20].单传家和夏云杰[21]研究了T-C模型中两原子的纠缠特性,但并未研究该模型中的GQD特性.

在本文中,我们考虑两个原子初始时刻处于纠缠态,并不忽略原子之间的偶极相互作用,研究GQD的演化规律及其受初始原子态、光场数和偶极-偶极相互作用强度的影响.

2 理论模型

考虑两个两能级原子与单模光场的相互作用,其原子间的偶极-偶极相互作用也被考虑在内.此情况下的系统哈密顿量H为(设～=1)

其中ω1和ω2为原子的本征跃迁频率,ω为腔场频率;a和a+分别是光子的湮灭和产生算符;g为原子与光场间的耦合系数;Ω为原子间偶极-偶极相互作用强度;σ,σ±1,σ±2为原子的自旋算符.

若|g⟩和|e⟩分别是原子的基态和激发态,则原子A的赝自旋算符为

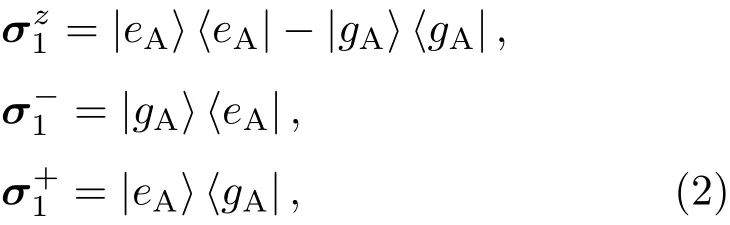
原子B的赝自旋算符为

在相互作用绘景中,考虑共振条件(ω=ω1=ω2),(1)式可变为

考虑共振情况且g1=g2,假设初始两原子处于纠缠态,光场处于粒子数态,则系统初始状态为

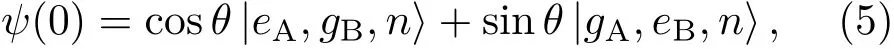
所以在任何时刻的态矢可表示为

将(4),(5)和(6)式代入相互作用绘景的薛定谔方程

通过计算可以得到

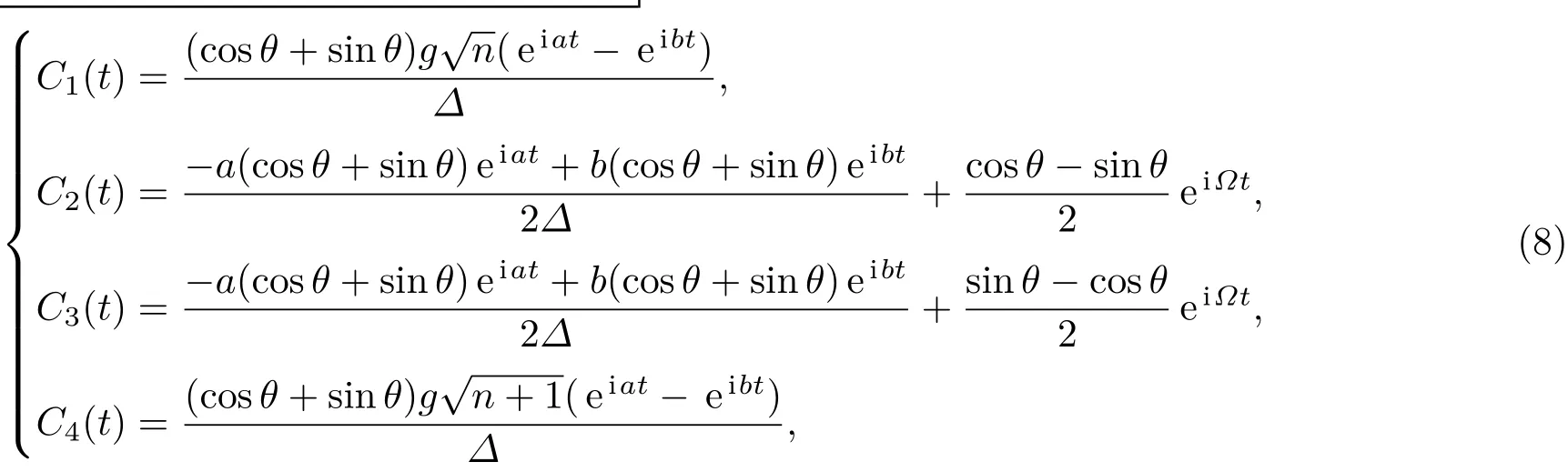
式中a=(−Ω − ∆)/2,b=(−Ω +∆)/2,∆ =

(6)式对光场求迹, 在原子基|ee⟩,|eg⟩,|ge⟩,|gg⟩下,约化密度矩阵ρAB(t)为

3 数值计算和讨论

Dakic等[12]提出了GQD,任何一个2 bit的量子态ρab都有如(10)式所示的Bloch表示:

式中xi=trρ(σi⊗ Ib),yi=trρ(Ia⊗ σi),tij=trρ(σi⊗ σj),x=(x1,x2,x3)T,y=(y1,y2,y3)T是边缘态ρa和ρb的Bloch矢量,而T={tij}是两体量子态的关联矩阵.ρAB的GQD为

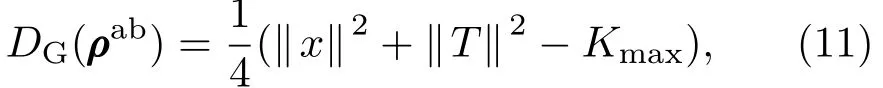
式中Kmax是矩阵K=x xT+TTT的最大本征值,上标T表示矩阵转置.利用(11)式进行数值计算,通过图1—图3展示GQD的演化规律.

图1描述的是改变两原子的初始状态时,GQD的演化规律.当θ=π/4,π/2时,GQD随时间周期性振荡,但可以发现当初态为最大纠缠态时,初始的GQD最大并随着时间减小到零后再回复至最大值;而初态为分离态时,GQD从零开始增大,减小到某个值时再增大后继续减小到零,但不能达到最大值.当θ=3π/8,5π/8时,初始时刻的GQD是一样的,但随着时间推移,图1(b)中曲线的GQD先减小到零之后恢复到初始值,而图1(d)中曲线一直处于失协状态并且GQD的值不会低于初始值.

图1 当g=1,Ω =1,n=0时GQD随时间t的演化 (a)θ=π/4;(b)θ=3π/8;(c)θ=π/2;(d)θ=5π/8Fig.1.Geometric quantum discord of two atoms as a function of the time for diff erent initial state(parameters:g=1,Ω =1,n=0):(a)θ= π/4;(b)θ=3π/8;(c)θ= π/2;(d)θ=5π/8.

图2 当g=1,Ω =1,n=1时GQD随时间t的演化 (a)θ=π/4;(b)θ=3π/8;(c)θ=π/2;(d)θ=5π/8Fig.2.Geometric quantum discord of two atoms as a function of the time for diff erent initial state(parameters:g=1,Ω =1,n=1):(a)θ= π/4;(b)θ=3π/8;(c)θ= π/2;(d)θ=5π/8.

图2描述的是改变腔场中的光子数,GQD的演化规律.从图中我们可以看到改变腔场的光子数量子GQD也是周期性演化.通过图1与图2的对比发现增加光子数后,使振荡周期变大并且长时间处于失协状态[如图1(c)和图2(c)所示],也会增强GQD强度,使失协强度更接近0.5[如图1(b)和图2(b)所示].当θ=π/4时,增加腔内光子数却加快了失协振荡频率[如图1(a)和图2(a)所示].

图3 当g=1,Ω =5时GQD随时间t的演化规律 (a)n=1,θ= π/4;(b)n=1,θ=3π/8;(c)n=0,θ= π/2;(d)n=0,θ=5π/8Fig.3.Geometric quantum discord of two atoms as a function of the time for diff erent initial state and diff erent Fock state of the fi eld(parameters:g=1,Ω =5):(a)n=1,θ= π/4;(b)n=1,θ=3π/8;(c)n=0,θ= π/2;(d)n=0,θ=5π/8.

图3 描述的是改变原子间偶极-偶极相互作用强度,腔中两原子的GQD的演化规律.对比图3与图2可以发现,增强偶极-偶极相互作用强度,GQD也是周期性振荡并使两原子一直处于失协状态[如图3(a)和图2(a)所示].当初态不为最大纠缠态时,增大偶极-偶极相互作用的强度,可以增大GQD并且可以增大振荡周期[如图3(b)和图2(b),图3(d)和图1(d)所示].并且发现一个有趣的现象是,当θ=3π/8时,增大偶极-偶极相互作用强度,进入腔后,GQD的值先增大,再减小,这与增加腔内光子数的情况有所不同.

4 结 论

通过改变两原子初始状态、腔内光子数和偶极-偶极相互作用强度,研究了T-C模型中的GQD特性.结果表明:选取适当的初态可以使两原子一直处于失协状态,同时发现适当地增强偶极-偶极相互作用强度可以使两原子一直处于失协状态.增加腔内光子数或增强偶极-偶极相互作用强度都可以使GQD有略微的增大.本文的研究结果对量子纠缠态制备、QD的操控有一定的指导意义.

[1]Ekert A K 1991 Phys.Rev.Lett.67 661

[2]Bennett C H,Brassard G,Grepean C,Jozsa R,Peres A,Wootters W K 1993 Phys.Rev.Lett.70 1895

[3]Shor P W 1992 Phys.Rev.Lett.52 2493

[4]Bogoliubov N M,Bulloughz R K,Timonenx 1996 J.Phys.A:Math.Gen.19 6305

[5]Zuo Z C,Xia Y J 2003 Acta Phys.Sin.52 2687(in Chinese)[左战春,夏云杰 2003物理学报 52 2687]

[6]Guo L,Liang X T 2009 Acta Phys.Sin.58 50(in Chinese)[郭亮,梁先庭 2009物理学报 58 50]

[7]Zhang G F,Bu J J 2010 Acta Phys.Sin.59 1462(in Chinese)[张国锋,卜晶晶 2010物理学报 59 1462]

[8]Ollivier H,Zurek W H 2001 Phys.Rev.Lett.88 017910

[9]Hu Y H,Tan Y G,Liu Q 2013 Acta Phys.Sin.62 074202(in Chinese)[胡要花,谭勇刚,刘强 2013物理学报 62 074202]

[10]He Z,Li L W 2013 Acta Phys.Sin.18 180301(in Chinese)[贺志,李龙武 2013物理学报 18 180301]

[11]Ali M,Rau A R P,Alber G 2010 Phys.Rev.A 81 359

[12]Dakic B,Vedral V,Brukner C 2010 Phys.Rev.Lett.105 4649

[13]Fan K M,Zhang G F 2013 Acta Phys.Sin.62 130301(in Chinese)[樊开明,张国锋 2013物理学报 62 130301]

[14]Hu M L,Tian D P 2014 Ann.Phys.343 132

[15]LI Y J,Liu J M,Zhang Y 2014 Chin.Phys.B 23 110306

[16]Chang L,Luo S 2013 Phys.Rev.A 82 034302

[17]Zhu H J,Zhang G F 2014 Chin.Phys.B 23 120306

[18]Song W,Yu L B,Dong P,Li D C,Yang M,Cao Z L 2013 Sci.China:Phys.Mech.Astron.56 737

[19]Xiao Y L,Li T,Fei S M,Jing N,Wang Z X 2016 Chin.Phys.B 25 030301

[20]Zou H M,Fang M F 2016 Chin.Phys.B 25 090302

[21]Shan C J,Xia Y J 2006 Acta Phys.Sin.55 1585(in Chinese)[单传家,夏云杰 2006物理学报 55 1585]