梯度磁场中自旋-轨道耦合旋转两分量玻色-爱因斯坦凝聚体的基态研究∗
李吉 刘伍明
1 引 言
两分量玻色-爱因斯坦凝聚体(BEC)[1,2],由于组分内相互作用与组分间相互作用两者互相竞争,为我们提供了一个全新的量子平台,可以研究许多有趣的拓扑缺陷[3−13].实验方面,Matthews等[2]在两分量BEC中产生了量子涡旋.Anderson等[3]观察到暗孤子在动力学过程中被分解为涡旋环.理论方面,Kasamatsu等[4]发现两分量BEC中的多畴是由调制不稳定性而形成的.Williams等[6]得到了多量子数涡旋.Öhberg和Santos[7]研究了两分量BEC中暗孤子的产生以及孤子间相互作用.一些研究者进一步详细讨论了旋转势下两分量BEC中的新奇拓扑结构和基态相图,例如四角涡旋晶格的动力学过程[9]、整数涡旋与分数涡旋的相变[10]以及不同涡旋结构的相图[11].此外,Battye等[12]证实了在两分量BEC中存在稳定的skyrmion结构.Martikainen等[13]理论研究了在两分量BEC中产生磁单极结构的方法.近年来,随着拓扑绝缘体和自旋霍尔效应的兴起,自旋-轨道耦合的研究吸引了人们广泛的关注.BEC由于其高度的可调控性,为实现和产生人造自旋-轨道提供了一个非常理想的平台.人们已经在超冷原子气体实验中实现了一维和二维形式的自旋-轨道耦合[14−17].许多研究者也在理论上提出了不同的实现方案[18−26].人造自旋-轨道耦合 BEC,由于原子内部自旋态和质心运动的耦合,进而提供了更多的机遇探索新奇量子态[27−33].Wang等[27]在无外势的自旋-轨道耦合两分量BEC中发现了平面波相和条纹相.如果考虑外势,体系将出现新的量子态,例如分数涡旋和涡旋格子[28]以及skyrmion格子[29].Bhat等[31]讨论了自旋-轨道耦合对调制不稳定性的影响.Kato等[33]研究了自旋-轨道耦合 BEC中涡旋-反涡旋对的动力学性质,并且发现在该体系中涡旋-反涡旋对的运动速度更慢.紧接着,人们研究了旋转势下自旋-轨道耦合两分量BEC的基态性质[34−44].例如,Xu和Han[34]在该体系中发现了对称排列的涡旋列和中心伴有巨skyrmion的三角涡旋格子.Liu等[35]发现在两分量BEC中自旋-轨道耦合能够诱导环形-双曲状的skyrmion.Zhou等[36]探讨了具有旋转和自旋-轨道耦合两分量BEC的基态性质,发现了半量子数涡旋格子结构.Fetter[42]详细讨论了自旋-轨道耦合BEC中的动力学行为.最近,人们利用磁场梯度实现了一些新奇量子态并观察到量子相变过程.有研究者利用梯度磁场方法实现了光晶格体系中的量子霍尔效应[45].此外,在BEC中借助梯度磁场,实验上观察到了人造磁单极结构[46,47]和量子扭结[48,49].之前的工作研究了梯度磁场中三分量BEC的基态结构,例如伴随极核涡旋的磁单极[50]和对称性排列的涡旋格子[51].然而,在两分量BEC中,梯度磁场和自旋-轨道耦合共同作用是否会导致新奇的基态结构和不同的基态相变,到目前为止这些问题依然不清晰.
本文研究了自旋-轨道耦合作用和梯度磁场对旋转两分量BEC基态的影响.研究结果表明,在梯度磁场中,随着自旋-轨道耦合强度增大,基态结构由skyrmion格子逐渐过渡为沿着对角线方向排列的skyrmion列.通过改变磁场梯度强度大小,深入探索该调控参数对系统基态结构的影响.发现当自旋-轨道耦合强度和旋转频率都小,磁场梯度的增强可导致基态由平面波相转变为half-skyrmion;当自旋-轨道耦合强度和旋转频率都大,梯度磁场可诱导hidden涡旋的产生.最后讨论了不同基态的自旋构型.梯度磁场作为自旋-轨道耦合两分量BEC中新的调控参数,能够控制和实现不同基态相间的转化.
2 理论模型
考虑梯度磁场和自旋-轨道耦合作用下的二维两分量旋转BEC体系,系统基态和动力学性质可由以下耦合的非线性方程组描述[35,50,51]:


其中Ψj(j= ↑,↓)描述凝聚体的原子分布在自旋向上态和向下态的宏观波函数,波函数满足条件N是体系内总粒子数;动能项中~为普朗克常量;m为选取87Rb原子的质量;二维光束缚势其中ω是束缚频率;旋转项中Ω代表旋转频率,其中规定Ω>0的正向旋转为逆时针旋转;ˆLz=−i~(x∂y−y∂x)是沿着z方向的轨道角动量;原子相同自旋态之间相互作用参量为原子不同自旋态间相互作用参量为
其中a11和a22是相同自旋态间的S波散射长度,a12是不同自旋态间的S波散射长度;梯度磁场项中[52−54],其中B′代表磁场梯度强度的大小,朗德因子gF=−1/2,µB为玻尔磁矩;考虑Rashba类型自旋-轨道耦合,κ表示自旋-轨道耦合强度的大小,px和py分别描述在x和y方向的动量算符.进一步可以得到无量纲化的耦合方程组[35,50,51]:

无量纲化波函数ψj=N−1/2ahΨj(j= ↑,↓),并且满足归一化条件无量纲化光束缚势无量纲化相互作用强度分别为g1=4πa11N,g2=4πa22N 和g12=4πa12N;散射长度选为a11=a22=100.40aB和a12=33.4aB,aB是玻尔半径;无量纲化的旋转频率,自旋-轨道耦合强度和磁场梯度强度分别为˜Ω,˜κ和B;谐振势的特征长度为在数值计算时,分别选用和ω~/(gFµBah)作为长度,时间,能量,自旋-轨道耦合强度和磁场梯度强度的单位.通过虚时演化方法求解(3)和(4)式得到基态[55−58],空间离散采用二阶中心有限差分,时间迭代采用线性项隐式和非线性项显式.数值计算网格为300×300,对应计算体系为12×12(a2h),初始试探函数为复数值的随机数.
3 研究结果与讨论
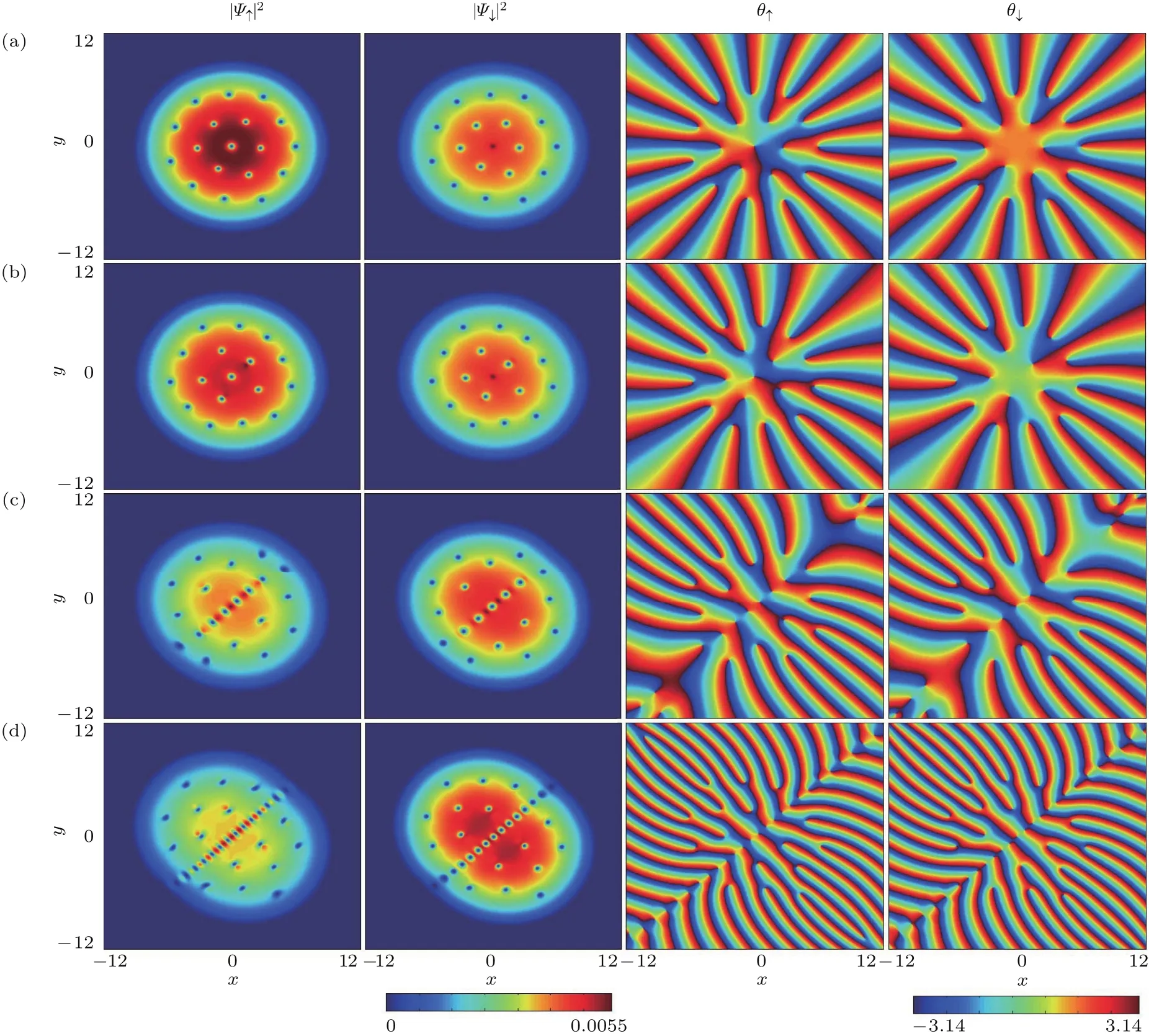
图1 不同自旋-轨道耦合强度下梯度磁场中两分量87Rb BEC基态粒子数密度分布(第1,2列)和相位分布(第3,4列)(a)˜κ=0;(b)˜κ=0.2;(c)˜κ=0.8;(d)˜κ=2;其余模拟参数选为g1=g2=6000,g12=2000,B=0.6,˜Ω=0.4和ω=2π×250 HzFig.1.Particle number densities(the fi rst and second columns)and phase distributions(the third and fourth columns)of ground state of the two-component BEC of 87Rb for the diff erent spin-orbit coupling strengths.The parameters are set as follows:(a)˜κ=0;(b)˜κ=0.2;(c)˜κ=0.8;(d)˜κ=2;and the rest of parameters are g1=g2=6000,g12=2000,B=0.6,˜Ω=0.4 andω=2π×250 Hz.
首先讨论自旋-轨道耦合对体系基态的影响.固定磁场梯度强度和旋转频率,利用虚时演化方法数值模拟得到不同自旋-轨道耦合强度下对应的基态结构.基态粒子数密度和相位分布如图1所示.第1,2列分别为自旋向上和自旋向下分量的密度分布,第3,4列分别为对应的相位分布.相位图中可以看到有许多相位割线,从割线蓝色一侧到红色一侧相位存在从−π到π的不连续跳跃.割线端点对应粒子数密度分布,图中密度极小值点即为涡旋核.当体系没有自旋-轨道耦合时,由于有旋转势存在,凝聚体各个自旋组分都会出现涡旋,如图1(a)所示.此外,由于产生涡旋的数目与旋转频率成正比,因此体系会出现一定数量的涡旋并以三角涡旋格子形式存在.其中每一个涡旋在自旋构型中实际上都对应一个skyrmion,因此也称此时的基态结构为skyrmion格子,下文将详细讨论.引入较小的自旋-轨道耦合强度˜κ=0.2,如图1(b)所示,三角涡旋格子排列规则稍微被打破,有一些涡旋开始偏离原来位置.进一步将自旋-轨道耦合增强到˜κ=0.8,发现凝聚体对角线方向出现整齐排列的涡旋列,尤其是处于中心对角线上的涡旋排列更紧密.同理,因为每个涡旋对应自旋构型上每个skyrmion,这样的涡旋列也被称为自旋空间下的skyrmion列,如图1(c)所示.从相位图中也可以看出,相位的奇异点表现为列状分布.在较强自旋-轨道耦合˜κ=2作用下,凝聚体基态依然保持为skyrmion列,而且排列分布更整齐,如图1(d)所示.因此,在梯度磁场中,改变自旋-轨道耦合强度,体系实现了从skyrmion格子到skyrmion列的转化.从物理角度也不难理解这样的现象:一方面,原子自旋和质心运动的耦合,会导致原子的自旋结构发生改变;另一方面,自旋-轨道耦合和梯度磁场共同作用,会改变体系内涡旋分布的对称性,使得涡旋排布从格子状转变为列状.与前人的研究结果相比,在没有梯度磁场的各向同性自旋-轨道耦合旋转BEC中,增加自旋-轨道耦合强度,体系基态仅仅支持skyrmion格子[35].
接下来,固定弱的自旋-轨道耦合强度,研究在不同旋转频率下梯度磁场对基态结构的影响.首先考虑旋转慢的情况,开始体系没有感受到梯度磁场,基态表现为平面波相,如图2(a1)所示.类似于无旋转自旋-轨道耦合两分量BEC中的结果,当组分内相互作用大于组分间相互作用,体系基态为平面波相[27].尽管此时有旋转,但是一方面旋转频率太小不足以产生涡旋,另一方面旋转势的作用小于规范势对体系的作用,所以只有平面波相出现.一旦体系考虑了梯度磁场,基态结构将发生变化.由于梯度磁场中心处为磁场零点,对应拓扑缺陷的奇异点,因此该磁场零点进入凝聚体中,便会引入产生一个拓扑缺陷,该缺陷对应自旋向上分量的粒子数密度分布中一个涡旋.从两个分量整体分析,一个分量表现为涡旋,另一个分量表现为孤子,这样的结构在文献中被称为半涡旋[55],如图2(a2)所示.实际上它对应自旋空间的一个half-skyrmion,下文将详细讨论.因此,当自旋-轨道耦合和旋转频率都小时,梯度磁场的引入实现了体系从平面波相到half-skyrmion的转变.进一步考虑旋转快的情况,没有外磁场时,体系出现大量涡旋,并围绕圆心以径向排列形成涡旋格子,如图2(b1)所示.当增大磁场梯度强度时,原来径向排列的涡旋格子结构被打破,中心处密度开始耗散,形成了椭圆状的环形结构.环形区域上的涡旋形成三角格子,环形内部及势阱中心区域形成巨涡旋,主对角线区域凝聚体粒子数较多,次对角线区域的凝聚体粒子数较少,如图2(b2)所示.这是因为强磁场梯度导致强的磁力,凝聚体原子很难聚在中心处,所以原子云从中心处扩散,形成不均匀的密度分布.此外,由于有旋转的存在,所以磁力和旋转两种作用相互竞争,出现了中心处的巨涡旋结构.
进一步,固定强自旋-轨道耦合,探索在不同旋转频率下梯度磁场对基态的影响.同样先考虑旋转慢的情况,当磁场梯度为零,强自旋-轨道耦合诱导两条互相垂直的涡旋列,如图3(a1)所示.在相位图中,被涡旋列分隔开的4个区域表现为平面波分布,而且相位值由小变大的方向为逆时针方向,正如黑色箭头所示.如果磁场梯度强度增强,发现体系结构仅仅表现为单列涡旋态,沿着倾斜方向排布,如图3(a2)所示.相位图中箭头表示平面波位相值的变化趋势.物理上不难解释,涡旋总是对应着自旋的剧烈翻转和起伏,这使得自旋偏离面内.而梯度磁场对原子的磁矩会产生作用,如果原来非面内的磁矩发生翻转,使得原子自旋沿着梯度磁场的方向,磁场对涡旋产生起一定的抑制作用,当磁场梯度变强时,抑制作用占主导地位,因此体系内涡旋数目变少.这种情况下,通过调节磁场梯度实现了两条互相垂直的涡旋列向单条涡旋列的转变.然后考虑旋转快的情况,在无磁场时,强自旋-轨道耦合和强旋转频率能够导致伴随巨涡旋的涡旋格子态,此结果也与前人的工作符合[34],如图3(b1)所示.当梯度磁场增大,发现凝聚态被挤压到主对角位置,这是由于强磁力所引起的.值得注意的是,体系内出现hidden涡旋[59],如图3(b2)所示.hidden涡旋是一种很有趣的拓扑缺陷,此类涡旋在密度分布中无法找到涡旋核,只能从相位图中观察到其相位奇异点.而且如同可见涡旋,自身能够携带角动量[59].图3(b2)中的hidden涡旋分布于体系次对角线区域,从相位图中可以清晰地看到,椭圆线圈之内的涡旋就是hidden涡旋.之前关于hidden涡旋的研究几乎都是基于单分量旋转BEC体系[59,60],这里提供了一种在两分量BEC中产生hidden涡旋的方法,为将来在高自旋BEC体系、超流和超导领域实现hidden涡旋提供了理论和实验指导.
最后讨论了不同基态的自旋结构,定义自旋平均值为[35,55]:

也给出了计算拓扑荷公式

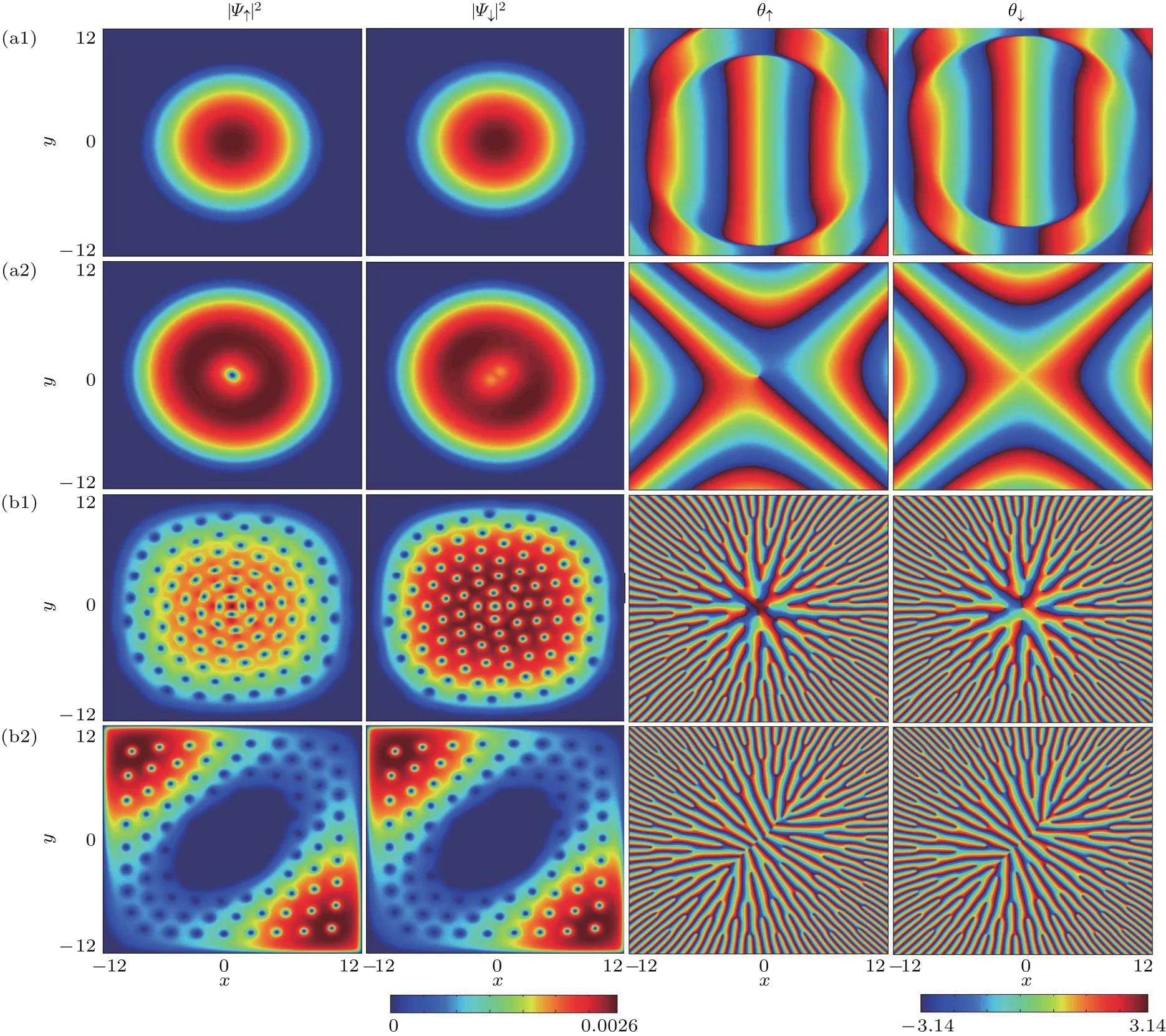
图2 在弱自旋-轨道耦合下,不同磁场梯度强度对基态的影响.第1,2列描述两分量87Rb凝聚体基态的粒子数密度分布;第3,4列表示对应的相位分布(a1)B=0,˜Ω=0.1;(a2)B=3.8,˜Ω=0.1;(b1)B=0,˜Ω=0.9;(b2)B=3.8,˜Ω=0.9;其余模拟参数选为g1=g2=6000,g12=2000,˜κ=0.8和ω=2π×250 HzFig.2.Eff ects of the diff erent magnetic fi eld gradient strength on ground state when the spin-orbit coupling is weak.The fi rst and second columns are the particle number densities of the two-component BEC of 87Rb;the third and fourth columns are the corresponding phase distributions.The parameters are set as follows:(a1)B=0,˜Ω=0.1;(a2)B=3.8,˜Ω=0.1;(b1)B=0,˜Ω=0.9;(b2)B=3.8,˜Ω=0.9;and the other parameters are g1=g2=6000,g12=2000,˜κ=0.8 and ω =2π×250 Hz.

图3 在强自旋-轨道耦合下,不同磁场梯度强度对基态的影响.第1,2列描述两分量87Rb凝聚体基态的粒子数密度分布;第3,4列表示对应的相位分布(a1)B=0,˜Ω=0.1;(a2)B=3.8,˜Ω=0.1;(b1)B=0,˜Ω=0.9;(b2)B=3.8,˜Ω=0.9;其余模拟参数选为g1=g2=6000,g12=2000,˜κ=4和ω=2π×250 HzFig.3.Eff ects of the diff erent magnetic fi eld gradient strength on ground state when the spin-orbit coupling is strong.The fi rst and second columns are the particle number densities of the two-component BEC of 87 Rb;the third and fourth columns are the corresponding phase distributions:(a1)B=0,˜Ω=0.1;(a2)B=3.8,˜Ω=0.1;(b1)B=0,˜Ω=0.9;(b2)B=3.8,˜Ω=0.9(the other parameters are g1=g2=6000,g12=2000,˜κ=4 andω=2π×250 Hz).
其中积分核为拓扑荷密度.图4(a)是对应于图1(a)的自旋结构,此时自旋-轨道耦合强度为零,体系中skyrmion形成三角格子排列,计算每个skyrmion对应的拓扑荷为1,属于整数skyrmion.通过分析体系内每个skyrmion的自旋结构,发现skyrmion自旋包括两种绕向及顺时针方向和逆时针方向.图4(a)圆圈中skyrmion的自旋结构是逆时针绕向,其对应的局部放大结构如图4(f)所示.值得注意的是,中心处表现为一个双曲型meron结构[51],这是由于梯度磁场所引起的.图4(b)是对应于图1(c)的自旋结构,当自旋-轨道耦合强度增大,原来的skyrmion格子转变为skyrmion列,沿着次对角方向排列.与此同时,关于次对角线对称的两个区域,面内自旋方向是相反的.此外,也发现体系内所有skyrmion自旋绕向都为顺时针方向,为了更清晰地看到自旋排布,给出了图4(b)三角形中skyrmion的局部放大结构,如图4(c)所示.图4(d)是对应于图2(a2)的自旋结构,自旋在面内呈现双曲四极分布,靠近中心处自旋发生翻转.计算拓扑荷为0.5,这样的自旋结构被称为half-skyrmion.图4(e)是对应于图3(a2)的自旋结构,当在强自旋-轨道耦合和慢的旋转情况下,梯度磁场的增强会导致体系内仅仅出现单条skyrmion列,而且沿着次对角线方向分布.此时体系内所有的skyrmion的自旋绕向为顺时针方向.
将来工作可以考虑具有其他形式的自旋-轨道耦合体系,例如Rashba-Dresselhaus自旋-轨道耦合 BEC,SU(3)自旋-轨道耦合 BEC和Weyl型自旋-轨道耦合BEC[61−63]等,此时基态结构将展现出更多有趣的特性.进一步,将考虑具有偶极相互作用和高自旋的BEC系统[64,65],由于长程各向异性的作用力和自旋交换相互作用,会对凝聚体的基态相貌、稳定性以及实时动力学性质产生显著影响,可以诱导更丰富的量子态和自旋纹理.

图4 基态的自旋结构 (a)对应图1(a)的自旋结构;(b)对应图1(c)的自旋结构;(c)描述图4(b)中三角区域自旋的局部放大结构;(d)对应图2(a2)的自旋结构;(e)对应图3(a2)的自旋结构;(f)描述图4(a)中圆形区域自旋的局部放大结构(自旋密度值变化区间为从−1(蓝色)到1(红色))Fig.4.The spin texture of the ground state:(a)Spin texture corresponding to the Fig.1(a);(b)spin texture corresponding to the Fig.1(c);(c)local enlargement of the spin in the triangular region in Fig.4(b);(d)spin texture corresponding to the Fig.2(a2);(e)spin texture corresponding to the Fig.3(a2);(f)local enlargement of the spin in the circular region in Fig.4(a)(Values of the pseudospin density are from−1(blue)to 1(red)).
4 结 论
本文利用准二维Gross-Pitaevskii方程,研究了自旋-轨道耦合和梯度磁场对旋转两分量BEC基态的影响,得到了不同参数下的基态结构.结果表明:自旋-轨道耦合与梯度磁场共同作用,能够导致体系基态由skyrmion格子转变为skyrmion列;当自旋-轨道耦合强度和旋转频率都小,磁场梯度强度的增大能够引起基态从平面波相到halfskyrmion的转化;对于自旋-轨道耦合强度和旋转频率都大的情况,梯度磁场可诱导体系产生hidden涡旋.最后,还讨论了基态的自旋结构.在自旋-轨道耦合BEC中,梯度磁场不仅仅对于研究奇异量子相提供了一个新的机遇,而且对于控制不同基态相间的转化发挥了关键作用.这些有趣的结果可为BEC中的相关拓扑激发实验提供指导.
[1]Hall D S,Matthews M R,Ensher J R,Wieman C E,Cornell E A 1998 Phys.Rev.Lett.81 1539
[2]Matthews M R,Anderson B P,Haljan P C,Hall D S,Wieman C E,Cornell E A 1999 Phys.Rev.Lett.83 2498
[3]Anderson B P,Haljan P C,Regal C A,Feder D L,Collins L A,Clark C W,Cornell E A 2001 Phys.Rev.Lett.86 2926
[4]Kasamatsu K,Tsubota M 2004 Phys.Rev.Lett.93 100402
[5]Qu C L,Pitaevskii L P,Stringari S 2016 Phys.Rev.Lett.116 160402
[6]Williams J E,Holland M J 1999 Nature 401 568
[7]Öhberg P,Santos L 2001 Phys.Rev.Lett.86 2918
[8]Kasamatsu K,Tsubota M,Ueda M 2004 Phys.Rev.Lett.93 250406
[9]Schweikhard V,Coddington I,Engels P,Tung S,Cornell E A 2004 Phys.Rev.Lett.93 210403
[10]Cipriani M,Nitta M 2013 Phys.Rev.Lett.111 170401
[11]Kasamatsu K,Tsubota M,Ueda M 2003 Phys.Rev.Lett.91 150406
[12]Battye R A,Cooper N R,Sutcliff e P M 2002 Phys.Rev.Lett.88 080401
[13]Martikainen J P,Collin A,Suominen K A 2002 Phys.Rev.Lett.88 090404
[14]Lin Y J,García K J,Spielman I B 2011 Nature 471 83
[15]Ji S C,Zhang J Y,Zhang L,Du Z D,Zheng W,Deng Y J,Zhai H,Chen S,Pan J W 2014 Nature Phys.10 314
[16]Wu Z,Zhang L,Sun W,Xu X T,Wang B Z,Ji S C,Deng Y J,Chen S,Liu X J,Pan J W 2016 Science 354 83
[17]Huang L H,Meng Z M,Wang P J,Peng P,Zhang S L,Chen L C,Li D H,Zhou Q,Zhang J 2016 Nature Phys.12 540
[18]Ruseckas J,Juzeliúnas G, Öhberg P,Fleischhauer M 2005 Phys.Rev.Lett.95 010404
[19]Campbell D L,Juzeliúnas G,Spielman I B 2011 Phys.Rev.A 84 025602
[20]Zhang J Y,Ji S C,Chen Z,Zhang L,Du Z D,Yan B,Pan G S,Zhao B,Deng Y J,Zhai H,Chen S,Pan J W 2012 Phys.Rev.Lett.109 115301
[21]Liu X J,Borunda M F,Liu X,Sinova J 2009 Phys.Rev.Lett.102 046402
[22]Anderson B M,Spielman I B,Juzeliúnas G 2013 Phys.Rev.Lett.111 125301
[23]Anderson B M,Juzeliúnas G,Galitski V M,Spielman I B 2012 Phys.Rev.Lett.108 235301
[24]Cheuk L M,Sommer A T,Hadzibabic Z,Yefsah T,Bakr W S,Zwierlein1 M W 2012 Phys.Rev.Lett.109 095302
[25]Wang P J,Yu Z Q,Fu Z K,Miao J,Huang L H,Chai S J,Zhai H,Zhang J 2012 Phys.Rev.Lett.109 095301
[26]Lan Z H,Öhberg P 2014 Phys.Rev.A 89 023630
[27]Wang C J,Gao C,Jian C M,Zhai H 2010 Phys.Rev.Lett.105 160403
[28]Sinha S,Nath R,Santos L 2011 Phys.Rev.Lett.107 270401
[29]Hu H,Ramachandhran B,Pu H,Liu X J 2012 Phys.Rev.Lett.108 010402
[30]Yu Z Q 2013 Phys.Rev.A 87 051606
[31]Bhat I A,Mithun T,Malomed B A,Porsezian K 2015 Phys.Rev.A 92 063606
[32]Li Y,Zhou X F,Wu C J 2016 Phys.Rev.A 93 033628
[33]Kato M,Zhang X F,Saito H 2017 Phys.Rev.A 95 043605
[34]Xu X Q,Han J H 2011 Phys.Rev.Lett.107 200401
[35]Liu C F,Fan H,Zhang Y C,Wang D S,Liu W M 2012 Phys.Rev.A 86 053616
[36]Zhou X F,Zhou J,Wu C J 2011 Phys.Rev.A 84 063624
[37]Sakaguchi H,Umeda K 2016 J.Phys.Soc.Jpn.85 064402
[38]Zhang X F,Gao R S,Wang X,Dong R F,Liu T,Zhang S G 2013 Phys.Lett.A 377 1109
[39]Wang X,Tan R B,Du Z J,Zhao W Y,Zhang X F,Zhang S G 2014 Chin.Phys.B 23 070308
[40]Wang H,Wen L H,Yang H,Shi C X,Li J H 2017 J.Phys.B:At.Mol.Opt.Phys.50 155301
[41]RadićJ,Sedrakyan T A,Spielman I B,Galitski V 2011 Phys.Rev.A 84 063604
[42]Fetter A L 2014 Phys.Rev.A 89 023629
[43]Chen G P 2015 Acta Phys.Sin.64 030302(in Chinese)[陈光平 2015物理学报64 030302]
[44]Liu C F,Liu W M 2012 Phys.Rev.A 86 033602
[45]Kennedy C J,Siviloglou G A,Miyake H,Burton W C,Ketterle W 2013 Phys.Rev.Lett.111 225301
[46]Ray M W,Ruokokoski E,Kandel S,Möttönen M,Hall D S 2014 Nature 505 657
[47]Ray M W,Ruokokoski E,Tiurev K,Möttönen M,Hall D S 2015 Science 348 544
[48]Hall D S,Ray M W,Tiurev K,Ruokokoski E,Gheorghe A H,Möttönen M 2016 Nature Phys.12 478
[49]Kawaguchi Y,Nitta M,Ueda M 2008 Phys.Rev.Lett.100 180403
[50]Li J,Yu Y M,Zhuang L,Liu W M 2017 Phys.Rev.A 95 043633
[51]Liu J S,Li J,Liu W M 2017 Acta Phys.Sin.66 130305(in Chinese)[刘静思,李吉,刘伍明 2017物理学报 66 130305]
[52]Leanhardt A E,Görlitz A,Chikkatur A P,Kielpinski D,Shin Y,Pritchard D E,Ketterle W 2002 Phys.Rev.Lett.89 190403
[53]Pritchard D E 1983 Phys.Rev.Lett.51 1336
[54]Leanhardt A E,Shin Y,Kielpinski D,Pritchard D E,Ketterle W 2003 Phys.Rev.Lett.90 140403
[55]Han W,Zhang S Y,Jin J J,Liu W M 2012 Phys.Rev.A 85 043626
[56]Dalfovo F,Stringari S 1996 Phys.Rev.A 53 2477
[57]Zhang X F,Dong R F,Liu T,Liu W M,Zhang SG 2012 Phys.Rev.A 86 063628
[58]Bao W Z,Du Q 2004 SIAM J.Sci.Comput.25 1674
[59]Wen L H,Xiong H W,Wu B 2010 Phys.Rev.A 82 053627
[60]Mithun T,Porsezian K,Dey B 2014 Phys.Rev.A 89 053625
[61]Ruokokoski E,Huhtamäki J A M,Möttönen M 2012 Phys.Rev.A 86 051607
[62]Barnett R,Boyd G R,Galitski V 2012 Phys.Rev.Lett.109 235308
[63]Chen G J,Chen L,Zhang Y B 2016 New J.Phys.18 063010
[64]Zhang X F,Zhang P,Chen G P,Dong B,Tan R B,Zhang S G 2015 Acta Phys.Sin.64 060302(in Chinese)[张晓斐,张培,陈光平,董彪,谭仁兵,张首刚 2015物理学报64 060302]
[65]Liu C F,Wan W J,Zhang G Y 2013 Acta Phys.Sin.62 200306(in Chinese)[刘超飞,万文娟,张赣源2013物理学报62 200306]

