《直线和圆的位置关系》教学设计

黑龙江省建三江管局前锋农场中学 戴秀丽

教学目标：

1.知识目标

（1）能够知道直线和圆相交、相切、相离三种位置关系的定义。

（2）利用定义来判断三种位置关系，会根据相切的定义画出圆的切线。

（3）利用圆心到直线的距离与圆半径之间数量关系表示直线和圆的位置。

（4）能利用切线知识进行简单的数学应用。

2.能力目标

引导学生通过观察分析，总结出圆心到直线的距离和圆的半径之间的数量关系，把直线和圆的位置关系利用数量关系表示出来。在总结应用的过程中进一步加强对分类讨论和归纳的思想有进一步的认识。

3.情感目标

通过创设情境导入新课，让学生观察素材,在一轮红日从海平面升起的动画中，提出问题，让学生能够根据学过的知识，把红日和海平面抽象出几何图形。引导学生用运动的观点观察圆与直线的位置关系的变化，让学生把实际的问题抽象成数学模型。

教学重、难点：

重点：掌握直线和圆的相离、相切、相交三种位置关系的性质和判定。

难点：引导学生发现三种位置关系中数量的不同。

教法设计：

采用引导启发、归纳总结的教学方法

学法指导：

采用小组讨论等方法，培养学生互帮互助的学习方法。引导学生自主归纳总结本节课学习的内容，培养和提升学生用数学语言归纳问题的能力。

教学准备：电脑课件、常用教学具。

教学过程：

活动一：复习引入（电脑课件展示）。

1.同学们，你知道点和圆有哪几种不同的位置关系？

2.你是用什么方法来判定点和圆的三种位置关系？

（1）点和圆心的距离大于半径时，点在圆外。

（2）点和圆心的距离等于半径时，点在圆上。

（3）点和圆心的距离小于半径时，点在圆内。

活动二：情境创设，定义探究。

1.观察日出图，感受直线和圆的不同位置关系。

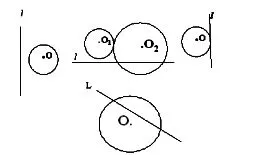
2.相离、相切、相交三种位置关系的定义总结：

如果直线和圆没有公共点，那么直线和圆相离.

如果直线和圆有一个公共点，那么直线和圆相切，这条直线叫圆的切线，这个公共点叫做切点。

如果直线和圆有两个公共点，那么直线和圆相交，这条直线叫做圆的割线。

定义运用：

下列直线和圆的位置关系分别是什么:

练习题（是是非非）：

（1）直线与圆最多有两个公共点 。…………………（ ）

（2）若C为⊙O上的一点，则过点C的直线与⊙O相切。……( )

（3）若A、B是⊙O外两点，则直线AB与⊙O相离。………( )

（4）若C为⊙O内一点，则过点C的直线与⊙O相交。（ ）

活动三：探究性质、总结关系。

观察后讨论:当直线与圆处于不同的位置关系时，圆心到直线的距离与半径有什么关系？

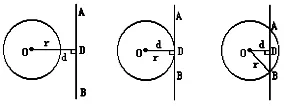
直线与圆 O相交 ＜=> d＜r

直线l与圆 O相切 ＜=> d=r

直线l与圆 O相离 ＜=> d>r

总结判断直线与圆的位置关系的方法：

（1）根据定义，由直线与圆的公共点的个数来判断；

（2）根据性质，由圆心距d与半径r的关系来判断。

活动四：新知运用。

1.经过圆上的点A用直尺近似地画出⊙O的切线.

2.圆的直径是13cm，如果直线和圆心的距离分别是

（1）4.5cm ； （2） 6.5cm ；（3） 8cm，

那么直线与圆分别是什么位置关系？ 有几个公共点？

活动五：切线的定义、判定。

1.填空：在⊙O中,经过半径OA的外端点A作直线L⊥OA,则圆心O到直线L的距离是多少?______,直线L和⊙O有什么位置关系?_________.

2.引导学生先观察图形，再描述切线的几何定义：经过半径的外端并且垂直于这条半径的直线是圆的切线.

例1 直线AB经过⊙O上的点C,并且OA=OB,CA=CB,

求证:直线AB是⊙O的切线.

练习1：

AB=AC，∠C=45°，以AB为直径作⊙O ，求证：AB是⊙O的切线

练习2

AC是直径，AB和CD是切线，判断AB和CD的位置关系

活动五：总结。

课后作业：1、圆与圆的位置关系。2、课后习题。