从古钱币谈几何命题

湖北省荆州市实验中学 付艺颖 付金雷

雨果说：“收藏家就是一批具有非凡毅力的普通人”.

收藏界“钱币为大，硬币为王” ，而价值不菲的硬币，多是古今中外的金银铜铁硬币，中国古钱币是文化艺术宝库中的一朵奇葩，萌芽于夏朝，殷朝得以广泛发展至今四千多年，古钱币设计思想精妙，将“天圆地方” 的宇宙观溶于钱币中，古钱币能够反映岀一个朝代一个民族在不同的社会环境政治背景下的文化，风俗，习惯，而古钱币又以铜币居多，特别是珍稀品，更是价值连城。我国古钱硬币虽品种繁杂(如图一) ，但大多数古钱币外形是圆形中要么开一个正方形的小孔，要么开一个小圆孔，要么不开孔，就又用一个或多个圆组成，这为几何命题提供了渊远历史背景，古人做人崇尚花好月圆，福禄寿喜俱全与花好月圆的大团圆并成人之美，做事堂堂正正，可方可圆，而初中平面几何亦覆盖做事为人内涵，点、线、三角形、四边形、相似形又在圆中“大团圆” 而 完美收官，下面就从众多古钱币中遴选几种作几何命题探究，以飨读者。

图一

1 “五帝钱”

五帝钱，是指清朝顺治、康熙、雍正、乾隆、嘉庆五个皇帝在位时发行的货币。五帝处于中国国力最强大的年代，时代相连，国运昌盛，社会安定繁荣，帝王独尊，百姓乐业，钱币铸造精良，流通时久，得“天、地、人”之精气，故能镇宅、化煞，并兼具旺财功能。以元宝，重宝，通宝为例构建命题这五位皇帝用的“方孔”钱和大多其他古钱一样都是，同心圆中开一个正方形的孔。(如图二) 会构建命题：

图二

(1)一枚圆形方孔钱（如图二）的外圆直径为a，中间方孔边长为b，则圆中实体面积为？()。

(2)某仿古钱币直径为4cm，钱币内孔边缘恰好是圆心在钱币外缘均匀分布的等弧(如图三).求钱币在桌面上能覆盖的面积为多少？(10.84cm2)。

图三

(3)如图四，一枚直径为4cm的中华民国古钱币沿着直线滚动一周，圆心移动的距离是？（4ηcm）

图四

(预设命题) 这个正方形有一个与钱币圆同心的外接圆。

图五

(再命题1) 如果画岀这个正方形的对角线(如图五)，那么∠OAB＝45°，∠OB’A’＝45°，于是A、B、B’、A’四点共圆，同理可证B、C、C’、B’，C、D、D’、C’，D、A、A’、D’，都分别共圆。

(命题2变式) 现在，我们把上述问题变换如下：

如图六，若以下各组点都共圆：(1) A、B、B’、A’(2) B、C、C’、B’(3) C、D、D’、C’(4) D、A、A’、D’(5) A、B、C、D，那么(6) A’、B’、C’、D’仍然共圆吗？(四边形A’B’C’D’不一定是正方形)

图六

证明：∵A、B、B’、A’共圆 ∴∠1=∠A’AB ，

∵B、C、C’、B’共圆 ∴∠2=∠C’CB，

∵C、D、D’、C’共圆 ∴∠3=∠C’CB

∵D、A、A’、D’共圆 ∴∠4=∠A’AD

∴∠1 + ∠2 + ∠3 + ∠4=∠DAB + ∠BCD

又∵A、B、C、D共圆 ∴∠DAB+∠BCD=180°

∴∠1+∠2+∠3+∠4=180° ∴A’、B’、C’、D’共圆

(命题3推论) 六组四点共圆，若有其中任何五组共圆，则最后一组四点必共圆。

2 “孙小头”

1912年是中华民国成立的开始，为了纪念这件翻天覆地的大事，国民政府决定铸银元纪念。1912年的民元国会。选举孙中山为第一领导人。铸造的首批银元以孙中山头像为背景图案。 开国纪念币为例实心同心圆，如图七作命题构想

(命题4)如图七，(1)内圆S1和圆环S2，S3有相同的圆心，且小圆S1和圆环S2,S3面积相等, 又S1,S2,S3对应的半径分别为R1,R2,R3则R23=________R21.(3)

(2) 若两条R2互相垂直，和圆环相交四点组成等腰梯形面积为25cm2，，则圆环的面积为多少？(50cm2)

图七

3.“四川铜币”

民国时期发行的一种货币。铜币是机器铸造的，少量翻砂造，铜元数量很大，是很重要的一个品类，甚至可以说是民国铜元的主体品种。1911年辛亥革命胜利后，清帝退位，中华民国成立，中华民国开国纪念币是由民国政府发行的一款纪念铜钱，正面“军政府造”字样，背面背“汉” 或交叉龙旗。铜币当时面值以当十、当二十，当五十，当一百为主，多数实心，尤其有大大小小的圆。

如图八 为例18个实心圆圈居多，因军阀混战，由于此古钱币为机制币，存在人为或模具磨损而岀现“错币”和“残币” ，比如岀现图五的“月牙儿币” 成为“趣味币” ，从而构建命题，多个实心圆

（1）(趣味币命题5) 如图八所示，在大圆周上有16个小圆圈，小明将其中一些不相邻的小圆圈涂成红色，这时无论再将哪个小圆圈涂成红色，都会使圆周上岀现两个相邻的红色小圆圈，问小明最少涂红了几个小圆圈？（6个）

图八

(2) (月牙儿错币命题6)如图九所示，在圆O中，弧ADB =90°，弦AB=a，以B为圆心，BA为半径画圆弧交于圆O于另一点C，则由两条圆弧所围成的月亮形(图中阴影部分)的面积s=？（ ）

图九

4.“花钱”

花钱源于汉代，花钱在早期是汉族民间自娱自乐的一种玩钱，这种钱币由于不是流通钱，因此它的材质和工艺大都比较粗糙。“花钱”虽然具有钱币的形态，但不作流通使用，是钱币中的“非正用品”。汉族民间花钱的种类繁多，五花八门，诸如开炉、镇库、馈赠、祝福、等等都要铸钱，这种“钱”，其实是专供某种需要的辟邪品、吉利品、纪念品，风花雪月品。其中“吉语钱”是比较普遍的一类花钱。主要以“长命富贵”、“福德长寿”、“加官进禄”、 “天下太平”等吉语为内容，这同时也反应了中国传统文化的渗透力。其珍稀美胜过官局制钱币，这一实一空同心圆构建命题。

(命题7)有两个半径差为2cm的圆，它们各有一个内接正十二边形(如图十)所示，已知阴影部分的面积是2016cm2，请问小圆的半径是多少？(167cm)

图十

5.“刀币”

春秋晚期至战国时期的燕国、齐国、赵国、中山国所通行的刀类货币 ，外形由同心圆和曲多边形组成，象一把“钥匙”，构建命题。

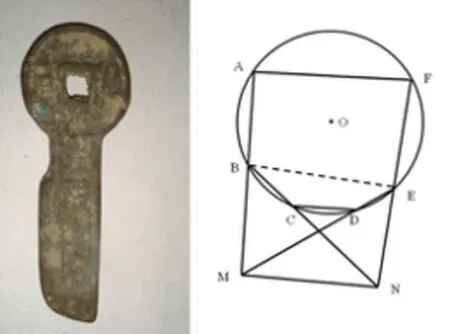
图十一

(命题8)如图十二＜1>若圆内接六边形ABCDEF对边CD//AF，对边AB,ED延长交于M，BC,FE延长交于N,则MN//CD.

事实上，本命题对于六边形ABCDEF不是凸六边形，六边形发生相交的情况亦是成立的。由此可演变出21个命题，下面选择几个罗列如下，它们证明方法罗列基本相同，不再一一写出，其余命题留作读后探究。

变式1：圆内接六边形ABCDEF的对角线AF与CD平行，对角线AB，DE交于M,BC,EF交于N,则MN//CD. (图十二＜2>)

变式2: 圆内接六边形ABCDEF边CD//AF,对角线MN//CD。(图十二＜3>)

变式3：圆内接六边形AECDBF对边CD//AF,对角线AB,ED延长线交于M,BC、FE延长交于N,则MN//CD. (图十二＜4>)

变式4: 圆内接六边形ABEFCD对角线AF//DC,对角线DE与边AB延长交于N,则MN//CD. (图十二＜5>)

变式5：圆内接六边形ABDCFE对角线AF//DC,对角线ED与边AB延长交于M，对角线BC与EF延长交于N,则MN//DC。(图十二＜6>)

变式1-5中，若仍看作六边形ABCDEF，则它不再是凸六边形，而回到命题8的形式。

图十二

不胜枚举，几千年古今中外硬币不计其数，从古钱币看几何图历史悠久，作图题，对称美，运动，点的轨迹无一不覆盖，建模命题也会取之不尽，用之不竭而丰富多彩，由模主要联想圆与圆位置关系及圆与正多边形关系，真是生活处处皆学问，古钱价值几何中有无限的几何呀！