织构拉刀的拉削负载特性建模与验证
倪 敬 舒 央 孟青新 吕俊杰 王书赢 胡春美
1.杭州电子科技大学机械工程学院,杭州,310018 2.浙江畅尔智能装备股份有限公司省级研发中心,缙云,321404
0 引言
拉削加工刀具(即拉刀)是航空航天、汽车等行业关键零部件高效精密拉削加工机床的核心部件,因其切削过程存在较大负载(一般不小于10kN),故刀具-工件-切屑之间摩擦磨损作用繁杂,不易被清晰地建模描述和实时检测反馈,如何深入地研究拉削刀具表面形貌,建立相应的拉削负载模型,降低拉削负载,减小拉刀的摩擦磨损,提高拉削过程的可靠性,是拉削加工行业中亟待解决的课题之一[1]。
国内外许多研究人员针对拉削刀具表面形貌与负载建模开展了研究。在刀具表面形貌研究方面,于占江等[1]发现将表面织构应用于车削刀具,可以有效减小切削力,减小刀具磨损量;邱孝聪等[2]介绍了表面织构的形态特征及其作用机制,讨论了织构分布、织构形状、表面粗糙度、速度和载荷等因素对润滑和摩擦学性能的影响;VLADESCUA等[3]通过实验研究了表面纹理对摩擦的影响以及混合和完全薄膜状态下织构的有利或不利影响;KHAIMOVICH等[4]提出了一种在高速加工中自动计算拉刀的应力、应变状态的函数和切削参数的方法。在拉削刀具负载建模方面,RAGHAVENDRA等[5]利用实验获得的拉削系统固有频率和实际阻尼固有频率来对拉削负载进行建模;SCHROETER等[6]基于动力学原理,构建并验证了拉削负载的动力学特性;KLOCKEA等[7]基于热诱导表面完整性、微观硬度和残余拉应力等参数,建立了拉削力模型;VOGTEL等[8]引入热力学原理,通过多元回归模型来预测拉削负载;HOSSEINI等[9]提出了拉削工具的几何模型和拉削负载的预测模型,基于切削系统中消耗的能量来预测切削力;倪敬等[10]考虑工件圆孔的圆弧效应、刀齿的刮削效应以及刀齿与工件接触的周期特性,建立了计算和预测拉削负载的模型。
然而,上述文献涉及的研究内容,一方面仅关注刀具织构表面能够降低切削负载,但是没有提出有效的切削负载模型;另一方面,现有切削负载模型大都将切削过程中刀具所受到的应力假设为均布应力,而没有很好地考虑刀具表面形貌对切削负载的影响。因此,诸如本文涉及的拉削刀具,其表面具有特殊的织构槽形貌,其刀具切削负载的详细计算模型有进一步研究的必要。
1 织构拉刀的拉削负载建模
1.1 拉削负载建模分析
图1所示为拉削加工系统,该系统主要由床身、主油缸、导向柱、溜板、夹刀装置、端板和织构拉刀等组成。具体拉削加工的工作原理为:主油缸通过溜板和夹刀装置驱动拉刀穿过工件圆内孔实现矩形槽的加工。

图1 拉削加工系统示意图Fig.1 Configuration of broaching machine
图1所示的拉削系统如果仅考虑织构拉刀与工件接触部分,可以简化为图2所示的原理图。图2中,刀齿的织构为凹形矩形槽;v为拉削速度;l1和l2分别为粗拉区和精拉区的长度;OXYZ为拉刀的拉削负载方向坐标系;lw为拉削工件的长度;p为拉刀上相邻两个刀齿的齿距,根据实际拉刀刀齿分布情况,p为一恒定数值;δi为第i个拉刀刀齿的绝对齿升量,i为拉刀刀齿序号,i=1,2,…,n,n为拉刀刀齿的齿数。
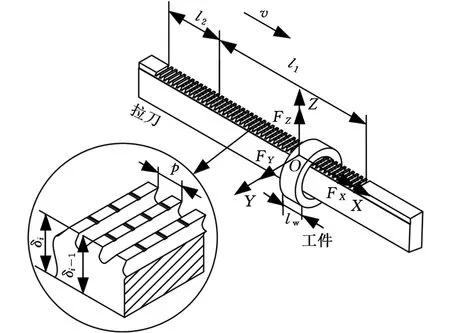
图2 织构拉刀及其负载分析图Fig.2 Load of broaching tool with texture
根据图2所示的织构拉削刀齿受力分析可知,织构拉刀的拉削负载主要由沿X方向拉削力FX、沿Y方向的正压力FY、沿Z方向的正压力FZ组成,其中又以沿X方向的拉削力FX为主要拉削负载,因此,本文以织构拉刀的拉削负载FX为研究对象开展建模分析。根据经典金属切削理论,FX可以描述为

式中,Ki为拉刀第i个刀齿与材料相关的比压力;Ai为拉刀第i齿拉削时的有效面积;βi为拉刀第i齿的量纲一常数。
根据图2和式(1)的描述,织构拉刀拉削负载特性具有以下特点:①由于每个刀齿上存在不同个数的织构槽,因此大大增加了拉削过程中Ai的复杂性,也增加了拉刀拉削负载预测的复杂性;②由于工件为内圆孔形状,因此拉削过程中很多刀齿与工件会不完全接触,即会产生圆弧效应;③由于工件存在长度,因此同时和工件接触的刀齿数存在变化。
基于上述分析,本文从经典单齿拉削负载模型入手,详细分析织构拉刀的拉削负载数学模型,然后考虑圆弧效应和多齿共同切削效应,建立一般性的织构拉刀拉削负载特性模型。
1.2 无织构槽单齿拉削负载模型
拉刀单个刀齿参与拉削情况出现在工件长度lw小于刀齿间距p的情况下。如图3和式(1)所示,根据经典切削加工理论,拉刀的拉削负载FX简化为单个刀齿拉削负载,可以具体描述为
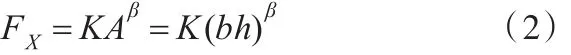
式中,K为与拉削刀齿材料相关的比压力;A为单齿拉削时的有效面积;b为刀齿宽度;h为刀齿切深;β为单齿拉削时的量纲一常数。

图3 无织构拉刀单齿切削参数图Fig.3 Configuration of broaching tool without texture
1.3 织构拉刀单齿拉削负载模型
1.3.1 单齿拉削负载模型
在织构拉刀单个刀齿上开设凹形织构槽的效果如图4所示。
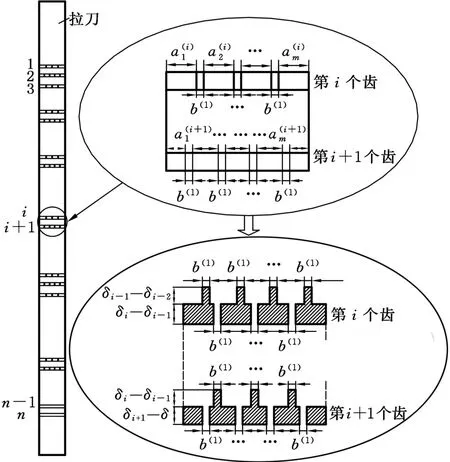
图4 织构拉刀的正视图Fig.4 Front view of broaching tool with texture
图4中,结合实际并为研究方便,假设拉刀第i个刀齿上开设的织构槽数m(i)为两个相邻的自然数,如3或4,4或5,等。这样,m(i)个织构槽将刀齿分成m(i)+1段,为第i个刀齿第j段刀齿
此外,如图 4所示,b(i)为第 i个刀齿后刀面开设凹型织构槽的宽度,则此时单齿参与切削的面积Ai1可以由下式计算:
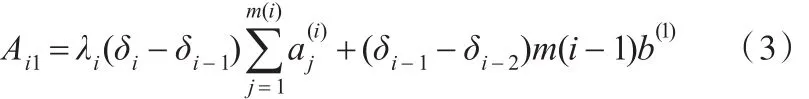
式中,m(i)为第i个刀齿的织构槽数量;λi为与比值相关的校正系数。
1.3.2 工件圆弧效应下的单齿拉削负载模型
根据图4所示的拉刀织构槽分布情况,拉削过程中,拉刀织构槽与工件之间的接触顺序如图5和图6所示。图6中,R为圆弧工件内圆半径,l0为工件圆弧中心到拉刀刀齿面的距离,δ0为第0个刀齿的绝对齿升量,Δδ=δi-δi-1表示相邻两个齿的绝对齿升量差,也就是单齿切深。依图5分析,拉削过程中,拉刀第k个织构槽碰到工件圆弧边缘时的拉刀齿序数nk可以由下式计算:

其中,符号‘[]’表示向上取整,‘’表示取余。

图5 拉刀织构槽与工件之间的接触顺序Fig.5 Contact between workpiece and tool with texture
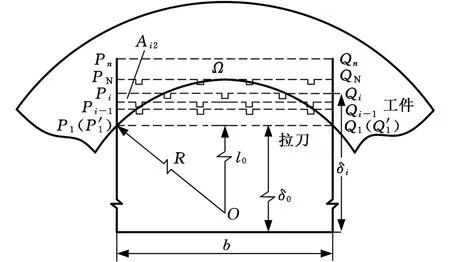
图6 工件圆弧效应下的Ai2计算原理图Fig.6 Calculation view of Ai2with round workpiece
于是,对工件圆弧效应下单齿参与切削的面积 Ai2分析如下。
(1)当i<n1时,圆弧效应下,织构槽未参与切削,则切削层剖面面积Ai2计算如下:

式中,Ai1为第i个刀齿的切削层剖面面积;S0为线段P1Q1和弧 P1ΩQ1组成的面积;Si表示线段和弧 P′iΩQ′i组成的面积。
S0和Si由下式计算:
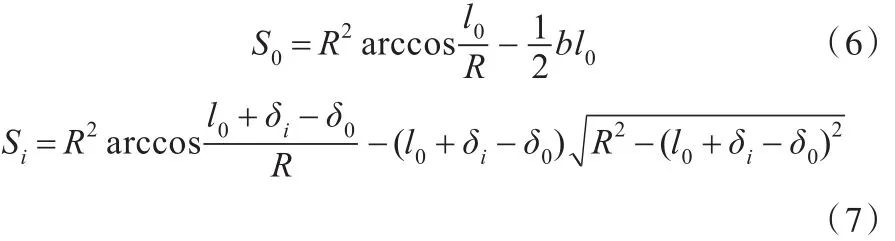
(2)当 n1≤i<nk时,圆弧效应下,织构槽阶梯性参与切削,则切削层剖面面积Ai2计算如下:

(3)当 nk≤i≤nN时,拉刀上的织构槽完全参与切削,其中,nN为拉刀切深达到PNQN线时的拉刀刀齿序号,即为圆弧效应分界点,则此时切削层剖面面积Ai2计算如下:

(4)当 nN<i≤n时,拉刀脱离圆弧效应,刀齿切削平面,则切削层剖面面积Ai2计算如下:

1.4 织构拉刀多齿拉削负载模型
根据图2所示的拉刀与工件的相互接触关系,一般情况下,工件长度lw都会大于拉刀刀齿间距p,这会导致与工件接触的拉刀齿数nc超过1个,即形成多齿拉削。该情况下,最大接触齿数nm与工件截面长度lw及拉刀齿距 p之间的关系可以表述为

实际拉削加工过程存在三个阶段,获得刀齿与工件的接触个数nc和时间t的关系如下所述。
(1)刀齿数增加阶段。在此阶段,nc每经过时间间隔Δt增加一个刀齿,一直达到nm,即

式中,t0为第一个刀齿接触工件所需时间;t1为nm个刀齿接触工件所需时间。
(2)刀齿数交替变化阶段。在此阶段,每经过时间间隔Δt,nc在整数nm与nm-1之间呈现周期变化特性,其接触刀齿数与时间关系可以表示如下:
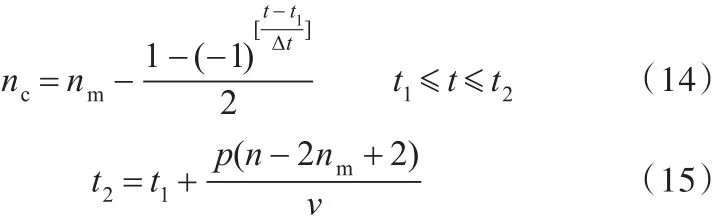
(3)刀齿数减少阶段。在此阶段,每经过时间间隔Δt,nc减少一个,一直达到0,其接触刀齿数与时间关系如下:

式中,t3为刀齿全部脱离工件所需时间。
综合上述分析可知,考虑工件圆弧效应下,多齿拉削负载动特性计算模型FX(t)可以描述为

式中,ni为参与拉削齿中将要脱离工件刀齿序数。
2 实验系统及参数
2.1 实验机床
实验机床为LG612Ya-800型拉床,如图7所示,主要由机床底座、控制台、主油缸(缸径100 mm,活塞杆直径50 mm,行程800 mm)、压力传感器、导向套、工件和拉刀组成。该拉削机床的额定拉力为20 kN,拉削加工速度为0~2.8 m/min。

图7 拉削加工实验系统Fig.7 Broaching experimental system
2.2 拉削实验工件与其制备
拉削实验测试所用工件材料为45钢,由外径60 mm和壁厚10 mm的钢管经过数控车削制成,具体形状和尺寸如图8所示。

图8 拉削实验工件造型图Fig.8 Configuration of workpiece
2.3 实验拉刀与其制备
2.3.1 实验拉刀
实验拉刀分为普通拉刀和其他织构槽拉刀两种。普通拉刀的材料为高速钢W18,具体形貌如图9所示,刀具的几何参数如表1和表2所示。普通拉刀的特征是每个刀齿上有3个或4个槽,槽数相邻交替变化,以完成整个平面的拉削加工。因此,可以称普通拉刀为3/4槽拉刀。

图9 织构槽拉刀的表面形貌Fig.9 Configuration of broaching tool with texture

表1 拉刀几何参数Tab.1 Geometry of broach tool
其他织构槽拉刀是以普通拉刀为基础,在每个刀齿上进行织构槽优化设计,因此,其他织构槽拉刀也可以称为4/5槽拉刀和5/6槽拉刀,其具体织构槽参数如表3所示。
2.3.2 实验拉刀制备
实验织构槽拉刀以普通键槽拉刀为基体材料,根据表3所示的织构槽参数,采用光纤激光打标机进行激光刻蚀得到,具体如图9所示。激光输出功率为20 W,激光波长为1.06 μm,重复频率为(20~2 000)kHz,雕刻线速度为0~7000 mm/s,最小线宽为0.03 mm,重复精度为±3 μm。

表2 拉刀刀齿齿升量参数Tab.2 Increasement of each broach tool mm

表3 拉刀后刀面织构槽参数Tab.3 Texture configuration on rear face of broach tool mm
2.4 拉削实验采集系统及实验方案
(1)实验采集系统。实验过程的拉削负载数据采集与分析采用自行研制的S7-300PLC监控系统完成,主要由数据分析软件、监控电脑、CPU313C、高速AI模块和压力传感器组成。拉削负载具体由主油缸两腔压力反馈检测间接求得,具体压力传感器为PTH503型,量程为0~15 MPa,输出信号为4~20 mA,综合精度为±0.5%FS,供电电压为24DCV,响应时间为5 ms。压力传感器的模拟量采集模块为高速AI模块,采样时间为1 ms,采样精度为14位。数据分析软件基于Borland C++Builder自行编制。
(2)实验方案。分别以3/4槽、4/5槽和5/6槽拉刀为研究对象,以相同的拉削速度45 mm/s进行拉削加工实验,实验数据采集时间为5.3 s,实验次数为每把刀具拉削3次。
3 实验结果验证与分析
3.1 织构槽拉刀拉削负载模型验证
根据前述实验方案,得到了重复性较好的拉削数据,任意选取3/4槽、4/5槽和5/6槽拉刀其中1次的拉削负载实验数据,可以得到图10~图12所示的织构槽拉刀拉削负载曲线。
(1)普通拉刀(3/4槽)的拉削负载验证。如图10所示的实验结果曲线,在0~0.9 s时间段,拉削力为0.5 kN,而此时这里的拉削力并不是真正的拉削负载力,而是主油缸的空载推力;在0.9~4.8 s时间段,这里的拉削负载是拉刀参与切削的拉削力体现。从曲线中可以看出,拉刀与工件的接触,拉削负载呈现由小变大的趋势;然后,由于受到了工件的圆弧效应影响,拉削负载继续增大,一直到圆弧效应消失时达到最大(大约在3.8 s);而后,拉刀刀齿的齿升量减小,拉削加工进入精密拉削过程(约到4.1 s),拉削负载呈现快速减小的趋势;最后,刀齿齿升量减小到0,进入拉挤过程,拉削负载经历一稳定阶段(约到4.8 s)后减小到空载情况。
根据织构槽拉刀的拉削负载计算模型(式(24)),对于3/4槽拉刀,Kj=2115.5,βj=0.082;这样可以得到图10中虚线所示的拉削负载仿真曲线。从图10中可以看出,仿真值和实验值吻合得较好,最大正偏差为0.3 kN,最大负偏差为-0.3 kN。也就是说实验测得拉削负载数据与仿真数据之间误差保持在4%内。因此,本文建立的模型可以较好地模拟3/4槽拉刀的实际拉削负载。
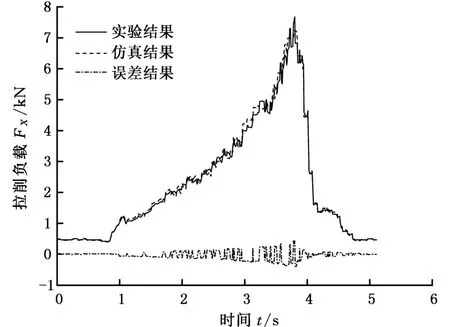
图10 3/4槽拉刀拉削负载仿真和实验曲线Fig.10 Load results of 3/4 type broach tool
(2)其他织构拉刀的拉削负载验证。根据织构槽拉刀的拉削负载计算模型(式24)),对于4/5槽拉刀,取 Kj=2115.5,βj=0.082;当≥3时,λi=1,当3时,λi=0.6。这样可以得到图11中的虚线所示的拉削负载仿真曲线。从图11中可以看出,仿真值和实验值吻合得较好,最大正偏差为0.2 kN,最大负偏差为-0.2 kN。也就是说,实验测得拉削负载数据与仿真数据之间的误差保持在3%内,因此,本文建立的模型也可以较好地模拟4/5槽织构拉刀的实际拉削负载。

图11 4/5槽拉刀拉削负载仿真和实验曲线Fig.11 Load results of 4/5 type broach tool
根据织构槽拉刀的拉削负载计算模型(式(24)),对于 5/6槽拉刀,取 Kj=2115.5,βj=λi=0.6。这样可以得到图12中虚线所示的拉削负载仿真曲线。从图12中可以看出,仿真值和实验值吻合得较好,最大正偏差为0.2 kN,最大负偏差为-0.2 kN。也就是说实验测得拉削负载数据与仿真数据之间误差保持在3%内,因此,本文建立的模型也可以较好地模拟5/6槽织构拉刀的实际拉削负载。

图12 5/6槽拉刀拉削负载仿真和实验曲线Fig.12 Load results of 5/6 type broach tool
综上所述,本文提出的织构拉刀拉削负载计算模型可以较好地模拟实际拉削负载。
3.2 刀齿表面织构参数对拉削负载的影响
将图10~图12中不同刀齿表面织构参数下实际拉削负载曲线放在一起,可以得到图13所示的结果。从图13中可以看出,当刀齿上的织构槽数量由3/4槽增加到4/5槽时,拉削负载有明显的减小;但是,当织构槽数由4/5槽增加到5/6槽时,拉削负载不是继续减小,反而增大了,增大到甚至比3/4槽时更大。
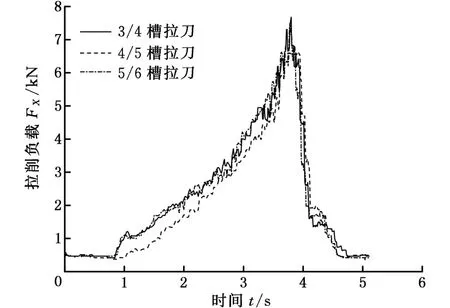
图13 不同织构参数下拉刀拉削负载对比Fig.13 Load comparison with different texture
另一方面,图10~图12中不同刀齿表面织构参数下实际拉削负载曲线的最大值和平均值放在一起,可以得到图14所示的结果。从图14中也可以看出,当拉刀刀齿上的织构槽数量由3/4槽增加到4/5槽时,拉削负载最大值由7.502 kN降低到7.076 kN(减小了约5%),拉削负载平均值由2.192 kN减小到2.016 kN(减小了约8%),都有明显的减小;但是,当织构槽数由4/5槽增加到5/6槽时,拉削负载最大值由7.076 kN上升到7.592 kN,拉削负载平均值由2.016 kN上升到2.541 kN,拉削负载最大值不是继续减小,反而增大了,增大到甚至比3/4槽时更大。

图14 不同织构参数下拉刀拉削负载平均值对比Fig.14 Average load comparison with different texture
根据上述不同刀齿表面织构参数下实际拉削负载趋势分析,拉刀表面的织构槽数量不是越多越好,而是有一个最优值。
根据式(5)~式(10)和式(24)的描述,结合图4,影响拉削负载的最主要因素是刀齿上的b(1)和数值。当长度相比于 b(1)较长时,待切削部分中 b(1)部分的加强作用不明显,忽略 b(1)部分对拉削负载并没有太大影响;而当长度减小到3倍的 b(1)时,待切削部分中 b(1)部分对整个切削部分起到了加强筋的作用,这使得切削加工变得困难,使得 b(1)和部分对拉削负载的贡献变得相当,即b(1)部分对拉削负载影响就不能忽略了。因此,拉刀刀齿上织构槽数量不是越多越好。
4 结论
(1)考虑拉刀刀齿表面的织构槽和工件圆弧效应,建立了单齿拉削负载模型。
(2)考虑由工件长度引起的多齿接触周期特性,得到了具有一般性的织构拉刀拉削负载计算模型。
(3)仿真与实验结果表明,在拉刀刀齿上开设织构槽可以减小拉削负载,但是开设的织构槽数量并非越多越好,而是存在一个最优值。对于宽度b=16 mm的拉刀,设置4/5织构槽降低负载效果最好。
[1] 于占江,王雯,张超楠,等.微型车刀微孔织构设计及高速微车削试验[J].润滑与密封,2016(2):18-22.YU Zhanjiang,WANG Wen,ZHANG Chaonan,et al.Design of Micro Hole Texture Tool and Experimental Study on High Speed Micro-turning[J].Lubrication and Seal,2016(2):18-22.
[2] 邱孝聪,樊曙天,伍勇.表面织构改善摩擦磨损性能的研究进展[J].润滑与密封,2013(8):121-124.QIU Xiaocong,FAN Shutian,WU Yong.Study of Surface Texture for Improving Friction and Wear Properties[J].Lubrication and Seal,2013(8):121-124.
[3] VLADESCU S C,OLVER A V,PEGG I G,et al.The Effects of Surface Texture in Reciprocating Contacts—an Experimental Study[J].Tribology International,2015,82:28-42.
[4] KHAIMOVICH A I,STEPANOV A A.Automated Calculation of Broaching Parameters[J].Russian Engineering Research,2015,35(8):615-616.
[5] RAGHAVENDRA K C,APPU K,TUGˇRULÖ.Mechanistic Force Modeling for Broaching Process[J].International Journal of Manufacturing Engineering,2014,2014:1-10.
[6] SCHROETER R B,BASTOS C M,CRICHIGNO J M.Simulation of the Main Cutting Force in Crankshaft Turn Broaching[J].International Journal of Machine Tools and Manufacture,2007,47(12/13):1884-1892.
[7] KLOCKE F,GIERLINGS S,BROCKMANN M,et al.Force-based Temperature Modeling for Surface Integrity Prediction in Broaching Nickel-based Alloys[J].Procedia CIRP,2014,13:314-319.
[8] VOGTEL P,KLOCKE F,PULS H,et al.Modelling of Process Forces in Broaching Inconel 718[J].Procedia CIRP,2013,8:409-414.
[9] HOSSEINI A,KISHAWY H A.On the Optimized Design of Broaching Tools[J].Journal of Manufacturing Science&Engineering,2013,136(1):507-513.
[10] 倪敬,顾瞻华,杨肖.内孔拉削动态负载计算模型[J].浙 江 大 学 学 报(工 学 版),2017,51(3):445-452.Ni Jing,GU Zhanhua,YANG Xiao.Dynamic Load Computing Model for Inner Hole Broaching[J].Engineering Journal of Zhejiang University,2017,51(3):445-452.

