影响小学生数感培养因素的研究——以《认识一个整体的几分之一》为例

张向林（特级教师）

长期以来，在应试教育的影响和传统教学思想的禁锢下,教师更多的是关注学生对知识的理解、掌握和解题能力的提高,片面地强调了学生的知识与技能,而忽略了对学生数感的培养。原有的小学数学教材体系中，对学生的数感重视不够。例如：对数的认识，往往偏重于对数的概念的建立，强调数的意义的理解而让学生估计和猜测的素材比较少。我们需要对教材进行“再加工”，创造适合学生的更好的“学材”，从而更有利于培养学生的数感。

当前很少一线教师关注和研究影响小学生数感培养的因素，缺乏挑战和怀疑教材的勇气，更少有批判精神，不敢否定和超越教材，也就难以发现教材中的不足，不利于学生数感的发展。对于数感的研究也多集中在对其涵义、构成要素的研究方面，由于理论性强、实践指导意义不够，往往收效甚微。下面以《认识一个整体的几分之一》教学设计与反思为例，谈谈我在这方面的实践与探索。

【教学内容】

苏教版三年级下册第76～78页例 1、例 2，以及“试一试”和“想想做做”。

【教学过程】

一、复习引入

1．谈话导入。

师：我们已经初步认识了分数，知道了把一个物体平均分成几份，这样的一份或几份都可以用分数来表示。

2．复习操作。

师：把一个桃平均分给2只小猴，每只小猴分得这个桃子的几分之几？

生：把一个桃平均分成2份，每份就是这个桃的。

（复习分数各部分的名称）

师：我们已经认识了一个物体的几分之一和几分之几。今天我们继续学习分数的知识。

（板书：认识一个整体的几分之一）

【设计意图：先呈现一个桃，提出把一个桃平均分给2只小猴，每只小猴分得这个桃子的几分之几？激活学生已有的“认识一个物体的几分之一”的经验，为新授做铺垫。】

二、探究新知

1.教学例 1。

讲述：一天，村里来了小猴一家——猴妈妈和一对可爱的小猴，村长特意买了桃子招待它们。

提问：一盘桃（6个）平均分给2只小猴，每只小猴分得这盘桃子的几分之几呢？

（学生独立思考，分组汇报讨论交流结果）

小结：把6个桃平均分给2只小猴，就是把这6个桃看成一个整体，平均分成2份，每只小猴分得一份，是这盘桃的。

提问：如果是4个桃，你会表示图中一盘桃的吗？

结论：把8个桃看成一个整体，把它平均分成2份，每只小猴分得一份，就是这盘桃的。

明确：把一盘桃平均分给2只小猴，就是把这盘桃看成是一个整体，平均分成2份，每份就是。

【设计意图：一个分数既可以表示一个具体的数量，也可以表示两个数量之间的相对大小关系。一盘桃有6个，多媒体演示把6个桃看成一个整体平均分成2份的过程，促进学生思考、领会：每份是3个桃，但它与这盘桃的关系仍用来表示。提升学生的抽象思维水平，有利于学生数感的形成。】

2.教学例 2。

师：如果村长把这盘桃平均分给猴妈妈、猴哥哥和猴弟弟，那么每份是这盘桃的几分之几？

（出示一盘6个桃图，让学生先分一分，再填一填）

（教师巡视，了解学生分的情况。交流、反馈学生分出的图形，指名说说是怎么分的，并解释表示什么意思）

3.如果把一筐桃平均分成2份，每份是这筐桃的几分之几？如果这筐桃是60个，平均分成2份，每份是这筐桃的几分之几？如果这筐桃是61个，平均分成2份，每份还可以用来表示吗？

4.出示教材第77页“试一试”。

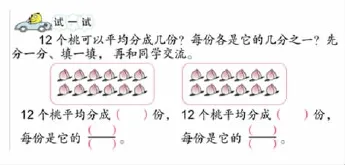
（学生动手分，教师巡视，了解学生分的情况。学生交流反馈，说说是怎么分的）

讨论：都是12个桃，表示每一份的分数为什么不同？

小结：我们已经知道把一个物体或一个图形，平均分成几份，其中的一份就是这个物体或图形的几分之一，可以用分数表示；今天的学习，我们又知道可以把几个物体，如2个桃、4个桃、6个桃、8个桃、60个桃、一筐桃等看作一个整体，把一些物体或整体平均分成几份，其中一份就是它的几分之一，也可以用分数表示。因为平均分的份数不同，表示每份与整体关系的分数也不同。

【设计意图：先呈现一个桃，提出：把一个桃平均分给2只小猴，每只小猴分得这个桃子的几分之几？从而激活学生已有“认识一个物体的几分之一”的经验，促进知识迁移。从一盘桃有6个，到一盘桃有4个、8个，突出6个、4个、8个桃都可以看作是一个整体，把它们平均分成2份，虽然每份桃的个数不相等，但每份都是这个整体的。这样安排，有利于学生逐步明晰“一个整体的”的含义，充分展现学习过程的价值，帮助学生形成数感，获得感悟。】

三、总结提升

师：通过本节课的学习，你有什么收获？还有哪些疑问？

【设计意图：总结提升环节，让学生进行自主交流，反馈学习的掌握情况。了解学生学习是否达到目标，强化学生的认知，有利于学生在现实生活中掌握知识，建立数感，让学生了解或表达“一个整体的几分之一”。本环节为小学生排除影响数感的因素，提升学生的数学素养。】

【教学效果与反思】

1.初步形成数感。

在新授时出示例1及情境图，并提出：一盘桃平均分给2只小猴，每只小猴分得这盘桃子的几分之几呢？学生很容易从“把一个桃平均分成2份，每份就是这个桃的”迁移到“把一盘桃平均分给2只小猴，每只小猴分得这盘桃子的”。把一盘桃盖住，先不让学生看出桃子的个数，可以有效避免桃的个数对新概念建立过程的干扰，有利于学生把思维聚焦于“一个整体”上，初步形成数感。

2.让学生在数学活动中形成数感。

平均的对象由一盘桃拓展为一筐桃，数量变化之大，也冲击学生的心理认知和预期，但内在的一致性得到了进一步的凸显。假设这筐桃的个数有60个、61个，学生在新的认知冲突中，进一步强化初步建立的数感认知，即：不管每份是几个，不管每份的个数是否为整数，它们都是一个整体的，让学生在数学活动中形成数感。3.在实际情境中获得数感。学生充分认识“一个整体的”的基础上，通过问题情境，引导学生认识一个整体的等等，有利于学生由特殊到一般，从抽象到理性的思维过程，完成对“一个整体的几分之一”的认识。学生在理解所学数的意义及表征后，建立起整体与部分之间的感悟，借助具体情境和图形，发展了一种数量的直觉，及用数字表现数量的感觉，在实际情境中获得数感。

4.针对教材中学生数感培养的例题和习题的诊断。

深入研读教材，根据《数学课程标准（2011版）》中对数感培养的要求，对例题和习题进行诊断和再设计；教师用修改加工前后的不同素材作为课堂教学的课程资源，通过实际的课堂教学检验，比较分析其对学生数学素养发展的影响。