沟通图式联系提升思维能力——《两积之和》教学实录与思考

姜 汇

【教学过程】

一、图形导入，初步感知

师：下面这两个是什么图形？会求它们的面积吗？

（学生口头回答，教师板书：6×7 10×12）

师：如果把这两个长方形平移到一起，它们有一条公共边，你能想象出是什么样子吗？会计算这个组合图形的面积吗？

生：只要把前面两个算式加起来就是组合图形的面积。

（教师板书：6×7+10×12=162）

【设计意图：对于学生来说，长方形比较直观，有利于几何模型的建立。从解决问题出发，让学生想象平移的过程，学生的思维更加积极主动。】

二、变化沟通，寻找联系

1.改变信息，提高难度。

师：我们能不能把已知的信息变化一下，提高一点难度呢？

生：可以把直接的信息改成间接的信息。

师：你是这个意思吗？说说你看懂这幅图了吗？你们会求它的总面积吗？

生：6×7+（18-6）×10=162。

师：还有其他方法吗？

生：我还可以把这个图形上下分割，这样算式就是：18×7+（10-7）×（18-6）=162。

师：说的真好!先说思路，再说方法。还有其他的方法吗？

生：我还有一种方法！把这个组合图形看成一个大的长方形，再去掉空白的部分，算式就是：18×10-（10-7）×6=162。

师：研究同一个问题，我们可以有不同的角度、不同的思路。

2.观察对比，确定主题。

师：请观察这三个算式，他们在结构上有什么相同的？

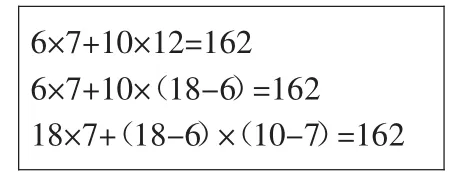
生：它们都是先算两个算式乘积再相加的。

生：它们的得数都是相同的。

师：像这样先分别求积，再求两部分的和，在数学上我们可以把它称为：两积之和（板书）。

师：那这样的算式18×10-（10-7）×6=162我们可以叫它什么呢？

生：两积之差。

师：同学们真会迁移，今天我们重点研究两积之和。

3.深入研究，反馈交流。

师：我们继续提高难度，哪里变了？

生：出现了未知数。

师：现在你还能写出像这样的两积之和的等式吗？

（学生独立研究，反馈交流）

师：（出示：162-12×10）÷7=△7×△+10×12=162）这两个算式你支持哪一种？为什么？

生：支持第二个算式，因为这是两积之和的结构。

师：那这两种方法之间有联系吗？

生：有联系，第一个算式就是把第二个算式反过来。

生：162是面积和，去掉12×10这个面积就能得到另一个长方形面积，再除以7就得到它的宽，第一个算式就是求未知数的。

师：你们真会观察，看来只要列出了两积之和的，等式我们就可以用第一种方法来求出图形代表的数。也就是说：第二个算式是两积之和的正运算，那第一个算式就是它的逆运算。

师：又发生了什么变化？你还能列出两积之和的算式吗？

生：未知数的位置发生了变化。

师：你还能写出两积之和的算式吗？

（学生独立列式，根据学生表述，板书：10×△+7×（18-△）=162 7×18+△×（10-7）=162）

师：这两组算式有什么不同？

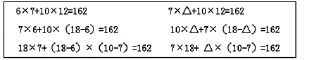
生：第一组没有未知数，第二组算式中出现了未知数。

师：虽然算式一次比一次复杂，无论有没有未知数，它们的主体结构都没有变化。我们都可以列出求两积之和的等式。

【设计意图：改编题目提高难度，虽然学生不太习惯，但很有价值，学生会有角色互换的感觉，这个过程他们需要进行更多的思考。让学生不解答应用题，通过多次观察、对比、联系感知无论信息怎样变化，求面积的基本方法都是不变的，从计算方法上都可以应用“两积之和”的数学模型，逐渐概括出几何模型和数量关系的联系。设计有未知数的信息参与，在交流讨论中分别呈现正向题和逆向题，强调“图”和“式”的联系，利用图去帮助分析数量关系。让学生可以借助几何模型将复杂的数学问题变得更加简单、明了，化难为易，从而感知模型的建立可以使数学问题的解决更加方便。进一步落实两积之和的数学模型。】

三、实际应用，体会价值

1．结合生活再次沟通。

例1.美术老师买了两种油画棒共18盒，一种每盒10元，一种每盒7元，7元的买了6盒，一共花去多少元？

师：这道题和下面这幅图之间有没有联系？先思考一下，再小组交流。

生：有联系。油画棒共18盒，就等于小长方形和大长方形的总长，10元就等于大长方形的边长，每盒7元是小长方形的边长，7元买了6盒，7×6就算出了小长方形的面积，两个长方形的面积就是两种油画棒的价格。

生：一共花去了162元，就是这个组合图形的总面积。

师：表述的真清楚，如果是租船问题你能把题目中的数量填到图中相应的位置吗？

例2.同学们去划船，一共租了18条船，小船每条坐7人，租了6条，大船每条坐10人，一共有多少人？

（学生独立填写，反馈交流，学生回答略）

师：在这个几何图形中我们找到了这两道应用题的影子，再和算式沟通联系起来，这就是一个两积之和的数学模型。

2.下面三幅图请你任选一幅图编一道用两积之和解决的问题。

生：我编的是第一幅图。去水果店买苹果，红苹果5元一个就是这个大长方形的宽，一共买了6个就是大长方形的长；青苹果是4元一个就是小长方形的长，一共买了3个就是小长方形的宽，一共用了多少钱就是小长方形的面积加上大长方形的面积，算式是：3×4+5×6=42。

（再请学生逐一交流第二、三幅图，并请学生互相点评）

【设计意图：数与形的联系不是一蹴而就的，需要循序渐进，螺旋上升。要让学生保持较高的学习兴趣，教师在设计问题时还要有一些挑战性。基本模型建立后还需要与生活建立联系，体会数学学习的价值。本环节从解决问题沟通图形和算式联系到给出几何图形让学生对应模型自主编题，从正向和逆向两个角度沟通联系代数问题与图形之间的互相转化、互相渗透、数形结合，是学生数学思维能力一个提升的过程。】