基于移动网格点云精简算法的研究
常 鑫,郎 锐,董建业
(中国电波传播研究所,山东 青岛 266107)
近年来,三维激光技术在测绘邻域的应用越来越广泛。然而由于通过扫描获取的点云数据具有冗余量大、存在误差以及规则性弱等特点,直接处理原始点云将会耗费大量时间和资源,因此一般在进行点云数据后处理之前都要进行预处理工作,包括点云去噪、点云精简、数据分块等等。点云精简是最为基本且非常重要的一步,同时也是逆向工程目前的研究热点之一。
点云精简最初的一些方法只是简单基于点之间距离、曲率、法向等原则,而目前点云精简的方法主要集中在以下几种典型方法:包围盒法、基于几何图像精简法、基于曲率精简法、基于法向精度精简法[1-7]。
国外很多学者早就在点云精简这一邻域探索出了很多解决方案。如Filip等人采用了包围盒法来精简点云数据[8],速度非常快,但只能用于处理均匀分布的点云;Alexa等人依据点云对最小二乘移动曲面的影响程度这一权重来进行点云的精简,且通过重采样保证了点云的密度[9],但其算法过程较为复杂;Chen.Y.H提出了先对点云进行三角网格化,通过精简三角网格数量来减少点云数量的方法[10],但往往构建三角网过程较繁杂。
国内学者针对点云精简也有很多研究,张丽艳在用Riemann图建立散乱测点间k邻近的基础上,提出了简化后数据集中点个数、数据集中点密度阈值及删除一点引起法向误差的阈值这3种简化准则进行点云精简[11],3种算法效率较高且精简效果较好,但是较算法中的邻近点个数K难以确定合适值;Xiao Z提出了一种非均匀点云的精简算法,主要依据各点与KD-tree包围球中心法向内积的阈值进行点云的精简[12],算法达到的精简效果很好,但是KD-tree包围球的半径难以计算,且法向内积计算量较大;王仁方等提出了基于几何图像的精简算法和随机采样方法[13],精简效率非常高,但容易丢失点云特征;倪小军提出了一种特征保留的点云自适应的精简算法,将点云划分为特征点和非特征点,保留特征点,而非特征点则通过计算自适应精简距离阈值进行精简处理[14],算法速度较快,能够较好地保留点云中的几何特征,但算法较依赖于点集的权重系数和初始设定的距离阈值。
基于上述分析总结,本文提出一种可移动网格划分的点云精简算法,该算法主要通过空间网格对点云进行精简,精简速度优势较明显,能够达到预期效果,且该算法中二次网格精简准则能够将上述算法的精简准则纳入其中。
1 大数据量点云精简的性能瓶颈
针对大数据量点云精简而言,如果直接依据给定距离阈值对点云模型进行空间网格划分,即将点云整个包围盒沿着空间3个方向划分成无数个小网格,分别在小网格内进行点云的筛选精简,通常为方便小网格的二分查找,小网格整体应按照其对应编码值按升序或降序排列,因此在进行每次二分插入时,通过二分查找确定相应位置后,所有该位置后的小网格数据都要往后推,涉及到大量数据的拷贝问题,从而产生大数据点云精简的性能瓶颈,其表现在随着原始点云个数的逐渐增加,精简消耗的时间越来越多,大大降低了精简的效率。为解决这一性能瓶颈,本文采用了在划分小网格之前先进行一次网格划分,对点云模型首先进行分块处理,使得小网格置于一次网格中,大大减少了小网格二分插入的时间消耗。
2 可移动网格划分算法
本文在基于其他已有研究成果的基础上,设计了一种可移动网格划分算法。算法首先对模型点云进行空间格网化,再依据距离阈值对已有的格网进行二次网格划分,依次遍历二次网格内点云,根据点云权重关系筛选出每个二次网格内保留下的点。二次网格划分结束后,平移点云整体包围盒最小点,对模型点云进行移动网格划分,最终筛选出所占权重较大的所有点云。
2.1 算法总体过程
算法具体过程可以分为以下3个模块:一次网格划分、二次网格划分、移动网格划分,其实现过程图如图1示。

图1 可移动网格划分算法实现过程
2.1.1 一次网格划分
点云模型的一次网格划分目的主要有两个,一是便于后期的二次网格划分的快速查找,二是筛选出点云个数大于给定点云个数阈值的区域。
在进行一次网格划分前,首先要进行空间三个方向的网格间隔计算。为了保证后期划分的二次网格不出现跨越一次网格的现象,就要使得一次网格间隔是二次网格间隔的整数倍。这里采用一种间隔估计算法,首先依据外业采集的三维激光扫描仪,确定其采样点分辨率,根据实际工程需求,选取适当的二次网格的间隔值为Interval,再根据其间隔和一次网格划分各方向的估计个数值GridXYZ,依据点云包围盒算出空间3个方向的包围盒边长存储于数组BoxSide[3]中,通过BoxSide[i]/(GridXYZ*Interval)(i=0,1,2)计算出结果并取整,得到各个方向上一次网格间隔相对于二次网格间隔的整数倍数N[3]。因此,一次网格间隔就为N[i]*Interval(i=0,1,2),重新按照BoxSide[i]/(N[i]*Interval)+1(i=0,1,2)计算出一次网格各个方向上的总个数。由于考虑到了取整问题,上述计算出的各个方向上的包围盒个数均增加了一个,从而保证点云不会超出一次网格。
网格间隔计算结束后,开始进行点云模型的一次网格划分。依据点云包围盒的最小点坐标值,通过式(1)计算出点云所处一次网格的三维脚码值II,JJ,KK。

(1)

为了方便后期查找一次网格,这里采用了一种线性编码方法。例如,上文求出的一次网格X、Y、Z 3个方向上的包围盒总数分别为Count1、Count2 、Count3,那么II、JJ、KK对应的编码值就为:II*Count2*Count3+JJ*Count3+KK。实质上就是将一次网格从空间上的三维排列变成了线性排列,如图2所示。依次遍历所有点云执行上述计算,相同编码值的点云存储于同一个一次网格内,每个一次网格主要存储编码值和所包含的点云数据,完成一次网格的初步划分。
待一次网格初步划分结束后,遍历所有的一次网格,筛选出点云个数超过给定的点云个数阈值的所有一次网格,并对这些一次网格再次进行一次网格划分,其中划分的个数估计值可改为GridXYZ/2。此时点云的包围盒不再是整体点云的包围盒,需重新进行计算,主要依据一次网格的编码值反算出对应的三维脚码值,从而再根据整体点云包围盒的最小值,计算出该一次网格的对应点云包围盒大小。迭代上述一次网格划分,直到一次网格中点云个数均少于点云个数阈值,完成一次网格划分的整个过程。
2.1.2 二次网格划分
二次网格划分主要目的是初步筛选出所有权重较大的点,其中每个二次网格中只存储一个点。在进行一次网格划分结束后,依次遍历所有一次网格,再在每个一次网格中遍历所有的点云。逐个取出单个点,根据式(1)同理计算出每个点的三维脚码值,再计算其对应的二次格网编码值。此时上文一次网格的线性编码方法不再适合,由于点云整体包围盒X、Y、Z 3个方向上所含有的二次网格数量过大,如果再采用上述一次网格的线性编码方法,那么二次网格的编码值会非常大,且会造成大量空网格出现,从而导致其编码值存储存在问题。因此这里舍弃一次网格的线性编码方法,采用任意线性编码方法,主要就是将一次网格线性编码的Count2、Count3换成两个给定的任意固定值(保持前者是后者的平方值即可),从而确保所有的二次网格编码统一化。
每次存储点云到二次网格中,都要进行筛选工作。计算出单点对应的网格编码值后,在当前一次网格内查找是否已保存过该编码值的二次网格。此处为了快速查找出是否存在已有编码值的二次网格,采用了二分查找方法,如果查找到该代码则返回对应的位置,否则返回其他值。经查找,如果未查找到,就创建一个二次网格,存储其编码值、该单点的坐标值以及该点的权重值(如,该点与当前二次网格中心的距离值、该点与扫描设备原点位置的距离值以及曲率值、法向值等),然后再二分插入到当前一次网格中,从而达到二次网格编码值按升序排列在一次网格中;如果查找到了,并获取到相应位置,则比较该单点的权重值p1和该二次网格中已存的权重值p0,如果p1>p0,则用该单点坐标和权重值p1替换二次网格中已保存的对应数据。
完成每个一次网格遍历后,将所有保留下的点云存储到二次网格中,同时清空对应的一次网格所有点云数据。当所有遍历结束后,便完成了二次网格划分整个过程。
2.1.3 移动网格划分
移动网格划分是本算法最核心部分,主要目的是对点云进行二次筛选。由于二次网格划分中存在一个问题,虽然每个二次网格中都存储了一个唯一的点,但是会出现两个点的权重值非常相近,却处在不同的二次网格中,从而导致很多密集点无法剔除的现象(如图3所示,图3(a)图中红色条状区域内即为密集点区域)。
通常情况下,采用的方法是将所有处于二次网格边缘的点筛选出来,存放于一个点云容器中。在单个边缘点存放前,首先遍历该容器中已存放的所有点云,筛选出与该边缘点距离小于二次网格阈值的点。若筛选到符合该条件的点,比较它们与该边缘点的权重值,存在权重值差异小于权重阈值的情况,则不存放该边缘点;否则存放。若没筛选到,直接存放该边缘点,从而解决了上述问题。但是,该方法在每次遍历容器中点云消耗的时间非常之多,导致整体上精简的效率非常的低。
另外如果不采用上述方法,采用单个二次网格邻域搜索法,遍历每个二次网格,通过搜索该二次网格周围邻近二次网格,寻找与该二次网格中的单点距离小于二次网格间隔的点,找到符合条件的点再进行权重比较,完成点云二次精简。但这种方法中每个二次网格最少会与周围4个二次网格、最多会与周围26个二次网格存在上述密集点云现象(如图4所示),情况非常复杂,因此在执行上会非常困难。
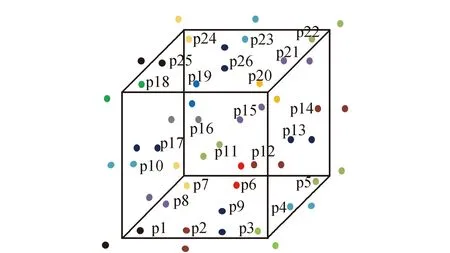
图4 密集点云分布示意图
为此,必须避免大量的点云数据遍历以及复杂的邻域搜索,本文提出了移动网格划分的思想,能够快速地解决上述问题。
移动网格划分主要是将点云包围盒的最小点进行平移,点云位置保持不变,重新依据新的包围盒的最小点进行二次网格划分。包围盒最小点3个方向上的平移距离值可为二次网格间隔值的K倍(其中0 为了实际分析和验证本文提出的算法性能,分别对不同点云模型进行精简实验,并将其结果与商业软件Geomagic精简结果进行对比分析。本实验的环境为:CPU:酷睿i5,内存:3.0 G,GPU:GeForce GTX 650,操作系统:Windows 7 SP1。 通过对不同大小点云数据进行测试,分别得到Geomagic精简和本文算法精简的最终成果点云和分别消耗的时间。其中精简消耗时间对比如表1所示,成果点云的效果图对比如图6所示。 图5 移动网格划分示意图 图6 精简对比 精简方法原始点云个数/万个精简后成果点云个数/万个消耗时间/sGeomagic软件距离精简13.373 52.50042.791 7110.380 327.10 0547.949 1511.784 177.000可移动网格划分精简1 118.908 310.296 90.15677.537 51.435383.222 732.386 针对本算法的精简效果准确性问题,采用误差度量方法:将精简后的点云P′进行三维重构,生成三角网模型,然后计算原始点云中所有点到该三角网模型的距离。分别用3项指标进行精简数据评估:Dmax、Davg以及Ratio,其中Dmax指的是原始点云集合P中所有点到精简后点云P′构建的三角网模型表面的距离最大值,Davg指的是原始点云集合P中所有点到精简后点云P′构建的三角网模型表面的距离平均值,Ratio指的是存在误差的区域占总体区域百分比。精简数据误差度量结果如表2所示。 表2 精简数据结果可靠性评估表 实验结果得出以下结论:从算法的精简效果以及效率对比可以看出,本算法精简的简度(精简后点云个数相对原始点云个数的百分比)明显降低,且在精度上很好地保留了点云的特征点,避免了点云“空洞”的现象发生,时间效率上也达到了明显的优势。 对于可移动网格划分的点云精简算法,主要时间消耗在二次网格的数据二分插入上,仍涉及到大量数据的拷贝问题,从而导致该算法整体速度减慢。 本文在点云模型的空间网格划分基础上,采用了可移动网格划分思想,对大数据点云进行了快速有效的精简。 1)算法在对点云直接进行二次网格划分前,先采用了一次网格划分,对点云数据进行了分块处理,将二次网格置于一次网格,大大减少了二次网格二分插入时所带来的时间消耗,整体上加快了点云精简的速率。 2)算法在进行二次网格划分结束后,即第一次点云精简后,采用了移动网格划分思想,很好地解决了点云密集无法剔除的问题。 3)算法在进行点云筛选精简时,能够很好地兼容其他算法所采用的点云精简准则,即算法中的二次网格所采用的权重值可为其他任何算法的权重值,如曲率值、法向值等等。 由于该算法中点云数据的二分插入仍然消耗了大量时间,降低了算法整体的精简速度,因此如何解决点云的快速二分插入问题需要进一步研究。 [1] 陈达枭, 蔡勇, 张建生. 散乱点云精简的一种改进算法[J]. 计算机应用研究, 2016(9):2841-2843. [2] 吴禄慎, 俞涛, 陈华伟,等. 基于自适应椭圆距离的点云分区精简算法[J]. 计算机应用与软件, 2016(2):42-45. [3] 刘迎, 王朝阳, 高楠,等. 特征提取的点云自适应精简[J]. 光学精密工程, 2017, 25(1):245-254. [4] 张雨禾, 耿国华, 魏潇然,等. 保留几何特征的散乱点云简化算法[J]. 计算机辅助设计与图形学学报, 2016, 28(9):1420-1427. [5] 律帅. 基于最小生成树的三维点云数据压缩算法研究[D]. 南京:东南大学, 2016. [6] 陈新河, 庞俊亭, 周波,等. 改进的分层曲率海量点云精简算法[J]. 计算机应用与软件, 2016, 33(4):265-267. [7] 麻卫峰, 周兴华, 徐文学,等. 一种基于局部曲率特征的点云精简算法[J]. 测绘工程, 2015(11):13-16. [8] ALEXA M, BEHR J, COHEN -OR D, et al. Point set surfaces[C]// Visualization, 2001. VIS '01. Proceedings. IEEE, 2001:21-28. [9] YUAN H, PANG J, JIANWEN M O. Research on Simplification Algorithm of Point Cloud Based on Voxel Grid[J]. Video Engineering, 2015. [10] CHEN Y H, NG C T, WANG Y Z. Data reduction in integrated reverse engineering and rapid prototyping[J].International Journal of Computer Integrated Manufacturing,1999,12(2):97-103. [11] 张丽艳,周儒荣,蔡炜斌,等.海量测量数据简化技术研究[J].计算机辅助设计与图形学学报,2001,13(11):1019-1023. [12] XIAO Z, HUANG W. Kd-tree Based Nonuniform Simplification of 3D Point Cloud[C]// International Conference on Genetic and Evolutionary Computing. IEEE, 2009:339-342. [13] 王仁芳,张三元,叶修梓.点模型的几何图像简化法[J].计算机辅助设计与图形学学报, 2007,19(8):1022-1027. [14] 倪小军.点云数据精简及三角网格面快速重构技术的研究与实现[D].苏州:苏州大学,2010.3 实例分析

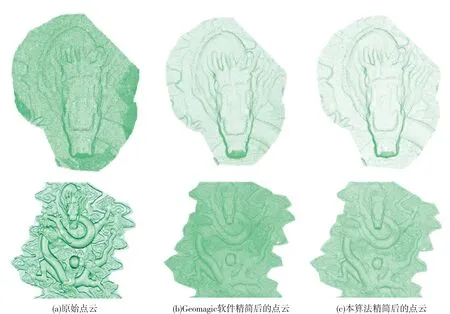
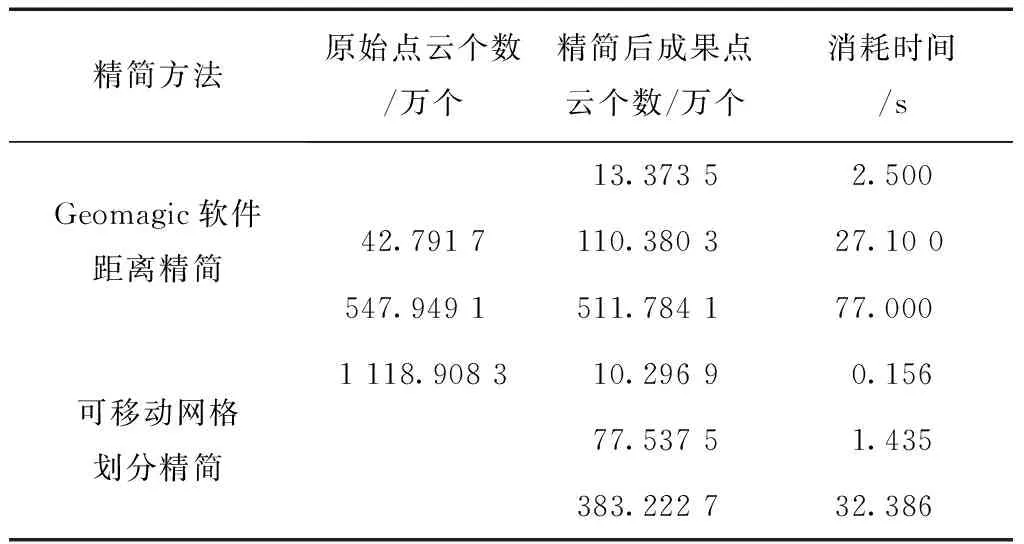

4 结 论

