一种基于激光测距仪的扫描匹配方法

刘 俊，李 霖,2

(1.武汉大学 资源与环境科学学院，湖北 武汉 430079；2.武汉大学 地球空间信息技术协同创新中心，湖北 武汉 430079)

激光测距仪因其快速、成本低、环境适应力强等特点，常被用作移动机器人的外部传感器[1]，扫描匹配通过计算使相邻扫描重叠最大的最优刚体变换，以此获取相邻时刻的运动量估计，广泛应用于移动机器人同步定位与环境建图(Simultaneous Localization and Mapping, SLAM)领域[1-10]。目前应用最广泛的扫描匹配算法是迭代最近邻算法(Iterative ClosestPoint, ICP)[1, 11-17]，但该算法对离群扫描点与稀疏扫描点较为敏感，由于缺少实际对应点，这些扫描点容易建立错误对应关系。此外，ICP算法根据最近点规则建立对应关系，可能存在一对多和对应距离极端大的问题[12-13]，这会影响最优变换计算的准确性，从而影响匹配的准确性。

Zhang等人提出一种单向对应的方法[13]，通过寻找多个最近点，根据其定义的规则选取某个点作为对应点，从而减少一对多对应，但该方法仍有可能建立对应距离极端大的对应关系。Chetverikov等人提出一种基于截断思想的迭代最近邻算法[18]，通过设置截断比例η，仅保留对应距离前η%的对应关系，从而剔除对应距离极端大的对应，但该方法对η参数较为敏感[19]，若η设置过大，可能保留对应距离极端大的对应，从而影响匹配的准确性，若η设置过小，可能剔除过多的对应关系，导致算法陷入局部最优。Pomerleau等人提出一种基于相对移动量的剔除方法[20]，但当旋转量较大时，剔除阈值的估算值并不准确[13]。

为了减少扫描数据中的离群扫描点和稀疏扫描点，本文提出一种基于连通格序列的方法，通过对扫描点进行空间网格划分并建立连通格序列，认为连通度较低的连通格是扫描数据的离群或稀疏部分，予以剔除，为ICP算法提供较为理想的输入；针对对应关系中的一对多和距离极端大的问题，本文通过建立唯一对应，避免建立一对多对应关系，并基于四分位数法[21]计算对应距离的上截断点，对应距离超过该截断点的为错误对应的可能性较大，予以剔除，减少错误对应数量，从而提高匹配的准确性。

1 ICP算法

ICP算法是目前应用最广泛的扫描匹配方法，其本质是一个“建立对应关系-求解最优变换”的迭代优化过程[22]，在每次迭代中，寻找参考扫描中最近点作为对应点，建立目标扫描与参考扫描的对应关系，基于该对应关系，求解一个使得目标函数最小的最优变换，并应用于目标扫描，作为下一次迭代的输入，直到达到收敛条件，最终实现两幅扫描贴合，并输出一个最优刚体变换。ICP算法步骤如下：

1)建立对应关系。对于目标扫描中的每一个点，寻找参考扫描中距离最近的扫描点作为对应点，建立对应关系。一般使用K-d树以加速最近点搜索过程[23]；

2)计算最优变换。计算一个最优变换，使以下目标函数最小，一般使用单位四元数法[23]求解旋转分量R和平移分量t；

(1)

3)应用最优变换。对目标扫描应用最优变换，得到新点集，作为下一次迭代的输入。

重复上述步骤，直到满足收敛条件或迭代次数超出限制。

2 扫描预处理

ICP算法采取点-点对应，对离群扫描点较为敏感，然而，由于室内环境的复杂性，激光测距仪在采集数据时可能会产生离群扫描点，如图1(b)所示，由于不存在实际对应点，这些离群扫描点容易建立错误的对应关系，如图1(c)所示。此外，在距离激光测距仪较远的区域，扫描点较为稀疏，这些稀疏扫描点容易建立方向上矛盾的对应关系，如图1(d)所示。因此，本文提出一种基于连通格序列的方法，通过对扫描点进行空间网格划分并建立连通格序列，认为连通度较大的连通格序列是扫描数据的主体部分，保留其范围内的扫描点，认为连通度较小的连通格序列是扫描数据的离群或稀疏部分，剔除其范围内的扫描点，从而为ICP算法提供较为理想的输入。

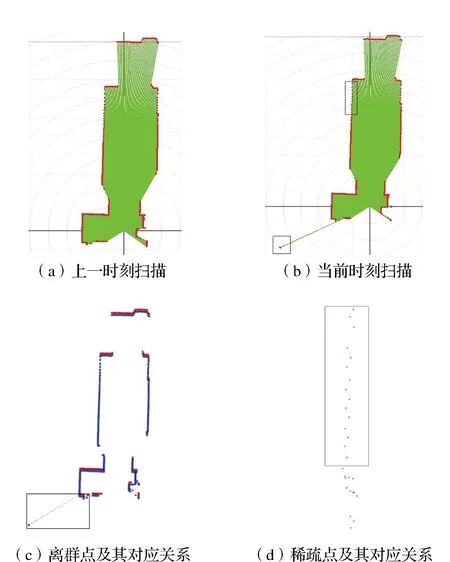
图1 离群点与稀疏点

首先，对所有扫描点进行空间网格划分。以传感器为坐标原点，计算所有扫描点的空间坐标，得到扫描点的最小外接矩形，根据一定的网格边长进行空间划分，如图2(a)所示，网格边长根据激光测距仪的分辨率与最大扫描距离决定，本文使用UTM-30LX激光测距仪，测量范围R=30 m，角度分辨率θ=0.25°，网格边长l=R|sinθ，取值为0.13 m。

接下来，获取连通格序列。网格分为占据格和空格，占据格内包含若干扫描点，空格内不包含扫描点，如图2(b)所示。首先，以第一个占据格G0为起点，初始化一个连通格序列，搜索G0的8邻域范围是否存在其他占据格G1；若存在，则将G1加入连通格序列，继续搜索G1的8邻域范围是否存在其他占据格；若不存在，该连通格序列建立完毕，以下一个占据格为起点，初始化一个新的连通格序列，重复上述过程。上述步骤一直执行，直到所有占据格都归属于某个连通格序列，如图3(a)所示。

最后，剔除离群扫描点与稀疏扫描点。定义连通格序列包含的占据格的数量为该序列的连通度，主体部分的扫描点较为连续，因此所归属的连通格序列的连通度较大，离群扫描点与主体部分距离较远，稀疏扫描点之间相隔较远，因此所归属的连通格序列的连通度较小。因此，通过剔除连通度较小的连通格序列内的扫描点，可以达到剔除离群扫描点与稀疏扫描点的目标。本文取最小连通度为5，判定连通度小于5的连通格序列内的扫描点为离群扫描点，予以剔除，结果如图3(b)所示，可以看出，离群点与稀疏扫描点被成功去除，扫描点的主体部分得以保留。

图2 网格划分

图3 扫描预处理

3 改进ICP算法

3.1 唯一对应

ICP算法假设目标扫描中每个点都存在实际对应点，然而，随着移动机器人探索新环境，以及环境中的动态障碍物等因素，该假设在实际应用中很难成立。例如，移动机器人在经过拐角时，传感器在上一时刻无法扫描到的障碍物，在当前时刻却可以扫描到，如图4(a)和图4(b)所示。ICP算法依据最近点规则建立对应关系，对于目标扫描中每一个点，选取参考扫描中距离最近的作为对应点，如图4(c)所示，可以看出，多个扫描点错误地对应参考扫描中同一个点，如图4(d)所示，这是由于这些扫描点不存在实际对应点，仍根据最近点规则建立对应关系所致，这些对应关系会显著影响最优变换计算的准确性。

因此，本文提出一种建立对应关系的新规则，通过限定每个参考点只能分配给最近的扫描点作为对应点，从而保证对应关系的唯一性，如图5(a)所示。例如，给定目标扫描中某扫描点pi，寻找参考扫描中距离最近点mj，作为候选对应点，判断mj是否已被分配给其他扫描点作为对应点，若未分配，则直接作为pi的对应点，若已分配给扫描点px，则比较pi和px到mj的距离，若pi距离更近，则替代px，并更新对应关系，否则跳过pi，不建立对应关系。根据该规则建立对应关系，结果如图5(b)所示，可以看出，一对多对应问题被成功解决。然而，该方法只能保证对应的唯一性，无法保证正确性，因此仍可能建立少数对应距离极端大的对应关系，在下一节将介绍一种稳健的剔除方法予以剔除。

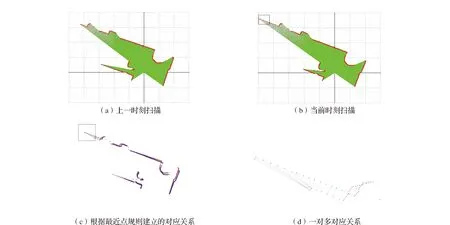
图4 根据最近点规则建立的对应关系

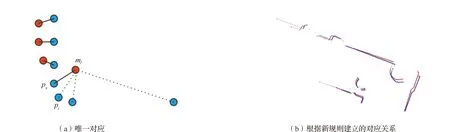
图5 根据新规则建立的对应关系

3.2 剔除对应

上述新规则只能保证对应关系的唯一性，无法保证其正确性，因此仍可能建立少数距离极端大的对应关系，这些对应关系为错误对应的可能性较大。因此，本文基于四分位数法计算对应距离的上截断点，剔除对应距离大于该上截断点的对应关系。

四分位数法是一种常用的异常值剔除方法，与传统的标准差法、Z分数法、经验法相比，具有简单方便、计算量小、受极端值影响小的优点，该方法将数据升序排列后划分为四个部分，每个部分包含25%的数据，Q1为第1四分位数(第25百分位数)，Q2为第2四分位数(第50百分位数)，Q3为第3四分位数(第75百分位数)，四分位极差R=Q3-Q1，在此基础上，该方法定义数据的上截断点为Q1-1.5×R，下截断点为Q3+1.5×R，判定大于上截断点的为极大值，小于下截断点的为极小值，从数据集中去除。以一组对应关系为例，对应距离的分布如图6(a)所示，根据四分位数法计算对应关系距离的上截断点为0.119，可以看出，大于该上截断点的仅有少数极端大的对应距离，根据该上截断点进行剔除，结果如图6(b)所示，可以看出，距离极端大的对应被成功剔除。

由于剔除目标主要是对应距离极端大的对应关系，因此，本文仅计算对应距离的上截断点dmax，剔除对应距离大于dmax的对应关系。dmax的计算步骤如下：

1)计算指数i。将对应关系按照对应距离升序排列后，根据i=(p/100)×n计算指数i，其中n为对应距离的项数，p为所求的百分位数的位置，例如求解第1四分位数，p为25；

2)计算第1四分位数Q1、第3四分位数Q3和分位数极差R。以计算Q1为例，若其指数i为整数，以第i项与第i+1项的平均值作为Q1的值，若i不为整数，将i向上取整后下标对应的值为Q1的值，同理求出第3分位数Q3。在此基础上，根据Q3-Q1求出R。

3)计算对应距离的上截断点dmax。根据四分位数法，上截断点定义为Q3+1.5×R，根据该定义，求解出对应距离的上截断点dmax。

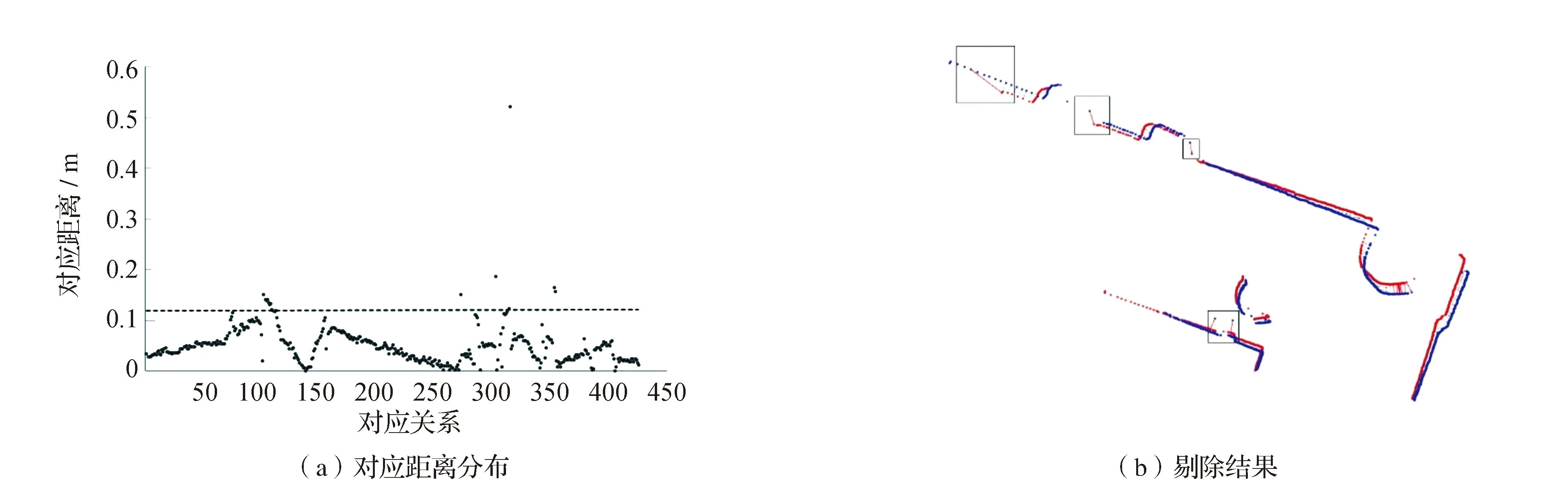
图6 基于四分位数法的剔除

4 试验结果及分析

4.1 实验设备

实验设备由一台移动小车和一个激光测距仪(UTM-30LX, Hokuyo Automatic Co. Ltd)组成，激光测距仪的最大测量距离为30 m，扫描角度范围270°，角度分辨率为0.25°，安装在移动小车前方，对室内环境进行水平扫描，获取二维扫描数据，如图7所示。

4.2 实验过程及成果

4.2.1 局部匹配实验

为了验证本文算法对于相邻时刻扫描的匹配效果，本文设计一组实验，实验选取一组相邻时刻的扫描数据，如图8(a)和图8(b)所示，可以看出，当前时刻扫描在矩形1区域中存在离群点，在矩形2区域中存在部分稀疏扫描点。

图7 实验设备及环境

为了验证扫描预处理对于匹配结果的影响，实验1以当前时刻原始扫描为目标扫描，上一时刻原始扫描为参考扫描，应用ICP算法进行匹配实验，实验2对当前时刻扫描进行预处理，以处理后的扫描作为目标扫描，上一时刻原始扫描作为参考扫描，同样应用ICP算法进行匹配实验。在建立对应关系阶段，实验1建立的对应关系如图9(a)所示，可以看出，由于目标扫描中存在离群点，且在参考扫描中缺少其实际对应点，从而产生错误对应，实验2建立的对应关系如图9(b)所示，可以看出，扫描预处理成功剔除了离群点与部分稀疏扫描点，但仍存在一对多对应和部分距离极端大的对应。实验1和实验2的匹配结果如图9(c)和图9(d)所示，可以看出，目标扫描与参考扫描间均存在较为明显的偏离，匹配结果都不理想，这说明扫描预处理仅能减少扫描中的离群点和稀疏点，但无法解决一对多对应和少数对应距离极端大的问题。

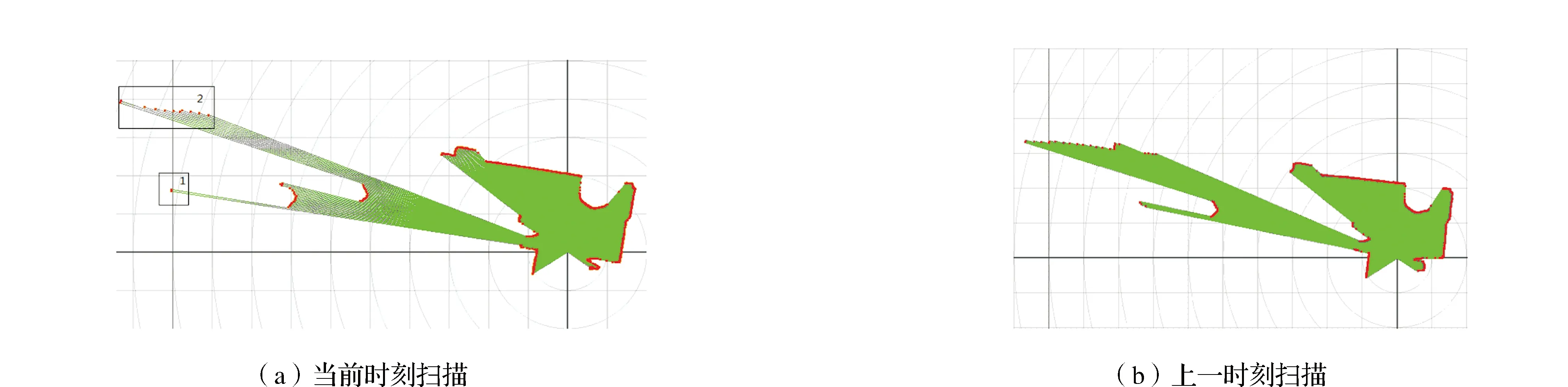
图8 相邻时刻扫描数据

图9 实验1与实验2

为了验证ICP改进算法处理一对多对应和距离极端大对应的效果，实验3与实验4均以扫描预处理后的当前时刻扫描为目标扫描，以上一时刻原始扫描为参考扫描，实验3应用ICP标准算法进行匹配，建立的对应关系如图10(a)所示，可以看出，对应关系中仍存在一对多对应和少数极端大的对应关系，其匹配结果如图10(b)所示，可以看出，扫描之间存在明显的偏离，匹配结果并不理想。实验4应用ICP改进算法进行匹配，建立的对应关系如图10(c)所示，可以看出，一对多对应和少数极端大的对应关系被去除，其匹配结果如图10(d)所示，可以看出，目标扫描与参考扫描紧密贴合，匹配结果明显改善。

4.2.2 全局匹配实验

为了验证本文方法在实际应用中的匹配表现，我们使用移动小车与激光测距仪采集了武汉大学化学院三楼部分走廊的扫描数据，在缺少里程计提供匹配初值的条件下，以第一幅扫描数据的坐标系为参考，分别应用ICP标准算法和本文算法，对所有相邻时刻扫描数据进行匹配实验，得到实验结果。ICP算法的匹配结果如图11(a)所示，可以看出，累计误差较大，匹配结果在走廊的后半段出现弯曲。本文方法的匹配结果如图11(b)所示，可以看出，匹配结果未出现明显弯曲，较好地表达了室内的平面结构，说明本文算法在实际应用中具有较好的匹配表现。

图10 实验3与实验4

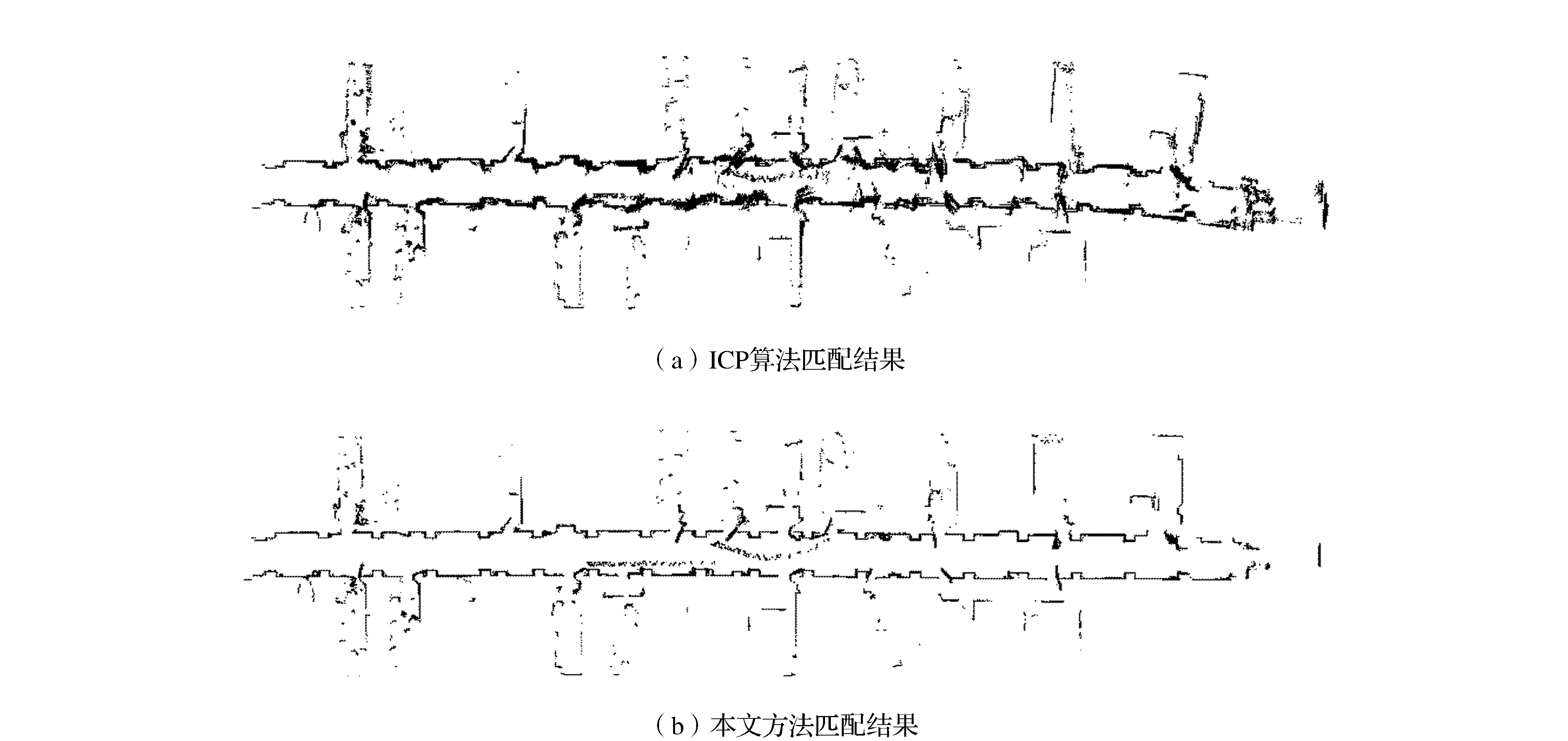
图11 实际应用匹配结果

5 结束语

为了剔除扫描数据中的离群扫描点和稀疏扫描点，本文提出一种基于连续格序列的方法，通过对扫描点进行网格划分并建立连续格序列，剔除连通度较小的网格内的扫描点，实现扫描数据的预处理，为扫描匹配提供较为理想的输入，实验结果表明，该方法能够有效剔除扫描数据中的离群扫描点和稀疏扫描点。此外，针对匹配过程中产生的一对多对应和距离极端大的对应，本文通过限定对应关系的唯一性，从而避免建立一对多对应，然后基于一种稳健的四分位数法计算距离阈值，剔除对应距离大于阈值的对应关系，从而减少对应距离极端大的对应关系，提高匹配的准确性，实验结果表明，本文方法能够较好地匹配相邻时刻扫描数据，且在实际应用中具有较好的全局匹配表现。

[1] LYU J, YUKINORI K, RAVANKAR A A, et al. A solution to estimate robot motion with large rotation by matching laser scans[C]. Society of Instrument and Control Engineers of Japan, 2015: 1083-1088.

[2] PEDROSA E, PEREIRA A, LAU N. Efficient localization based on scan matching with a continuous likelihood field[C]. IEEE International Conference on Autonomous Robot Systems and Competitions, 2017: 61-66.

[3] 钱晓明, 张浩, 王晓勇,等.基于激光扫描匹配的移动机器人相对定位技术研究[J]. 农业机械学报, 2016, 47(3): 14-21.

[4] WANG X, JIA Y, XI N, et al. Mobile robot pose estimation using laser scan matching based on Fourier Transform[C]. IEEE International Conference on Robotics and Biomimetics, 2014: 474-479.

[5] LIU Y, SUN Y. Mobile robot instant indoor map building and localization using 2D laser scanning data[C]. International Conference on System Science and Engineering, 2012: 339-344.

[6] DIOSI A, KLEEMAN L. Fast Laser Scan Matching using Polar Coordinates[J]. International Journal of Robotics Research, 2007, 26(10): 1125-1153.

[7] MINGUEZ J, MONTESANO L, LAMIRAUX F. Metric-based iterative closest point scan matching for sensor displacement estimation[J]. IEEE Transactions on Robotics, 2006, 22(5): 1047-1054.

[8] DIOSI A, KLEEMAN L. Laser scan matching in polar coordinates with application to SLAM[C]. Ieee/rsj International Conference on Intelligent Robots and Systems, 2005: 3317-3322.

[9] PFISTER S T, KRIECHBAUM K L, ROUMELIOTIS S I, et al. Weighted range sensor matching algorithms for mobile robot displacement estimation[C]. IEEE International Conference on Robotics and Automation, 2002. Proceedings. ICRA, 2002: 1667-1674 vol.2.

[10] BENGTSSON O, BAERVELDT A J. Localization by Matching of Range Scans - Certain or Uncertain?[C]. Eurobot, 2001.

[11] 顾文华, 周波, 戴先中.基于ICP匹配算法的室内移动机器人定位[J]. 华中科技大学学报(自然科学版), 2013, 41(增1): 262-266.

[12] POMERLEAU F, COLAS F, SIEGWART R, et al. Comparing ICP variants on real-world data sets[J]. Autonomous Robots, 2013, 34(3): 133-148.

[13] ZHANG L, CHOI S I, PARK S Y. Robust ICP Registration Using Biunique Correspondence[C]. International Conference on 3d Imaging, Modeling, Processing, Visualization and Transmission, 2011: 80-85.

[14] CENSI A. An ICP variant using a point-to-line metric[C]. IEEE International Conference on Robotics and Automation, 2008: 19-25.

[15] ZHU J, ZHENG N, YUAN Z, et al. Point-to-line metric based Iterative Closest Point with bounded scale[C]. Industrial Electronics and Applications, 2009. Iciea 2009. IEEE Conference on, 2009: 3032-3037.

[16] RUSINKIEWICZ S, LEVOY M. Efficient Variants of the ICP Algorithm[M]. 2001: 145-152.

[17] 洪斌斌, 孟正大.基于MBlCP匹配算法的陪护机器人定位方法[J]. 工业控制计算机, 2015, (9): 42-44.

[18] CHETVERIKOV D, SVIRKO D, STEPANOV D, et al. The Trimmed Iterative Closest Point Algorithm[C]. 16 Th International Conference on Pattern Recognition, 2002: 30545.

[19] ZHU J, MENG D, LI Z, et al. Robust registration of partially overlapping point sets via genetic algorithm with growth operator[J]. Iet Image Processing, 2014, 8(10): 582-590.

[20] POMERLEAU F, COLAS F, FERLAND F, et al. Relative Motion Threshold for Rejection in ICP Registration[M]. Springer Berlin Heidelberg, 2009: 229-238.

[21] 巩斌, 丁华军. 在统计分析中如何快捷识别极端值[J]. 统计与咨询, 2007, (3): 14-15.

[22] 王育坚, 廉腾飞, 吴明明, 等. 基于八叉树与KD树索引的点云配准方法[J]. 测绘工程, 2017, 26(8): 35-40.

[23] 刘江, 张旭, 朱继文. 一种基于K-D树优化的ICP三维点云配准方法[J]. 测绘工程, 2016, 25(6): 15-18.